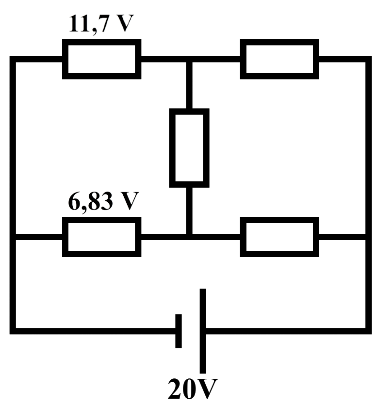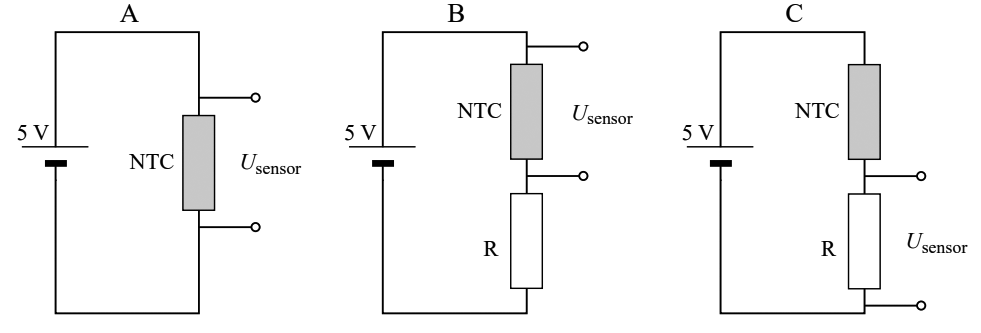Hoofdstuk 7
Elektriciteit

§1 Lading

In dit hoofdstuk gaan we elektriciteit bestuderen. Omdat elektriciteit bestaat uit bewegende ladingen, gaan we in de eerste paragraaf eerst kijken naar het begrip lading. Dit doen we aan de hand van de begrippen stroomsterkte en spanning. Ook gaan we elektrische schakelingen bestuderen en introduceren we een aantal onderdelen, zoals de NTC en de LED.

Zoals je weet bestaat materie uit atomen. In de atoomkern bevinden zich deeltjes met een positieve lading genaamd protonen. Deze protonen zijn relatief zwaar en zitten stevig vast in de atoomkern. Om de atoomkern heen bewegen een aantal deeltjes met een negatieve lading genaamd elektronen. Deze deeltjes zijn relatief licht en bewegen met enorme snelheid om de atoomkern. Het zijn deze negatieve ladingen die zorgen voor elektriciteit.

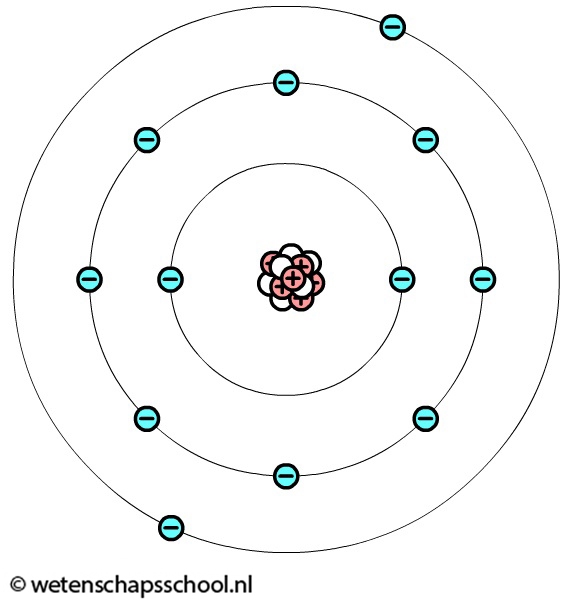
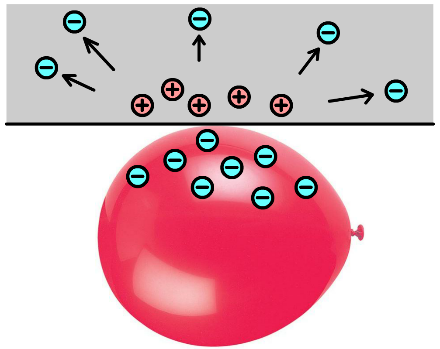
De positieve en de negatieve ladingen hebben de bijzondere eigenschap dat ze elkaar aantrekken. Daarnaast is het zo dat ladingen van dezelfde soort elkaar afstoten. Deze effecten zien we bijvoorbeeld als we een ballon tegen een trui wrijven. Door de wrijvingskracht komen elektronen van atomen uit de trui op de ballon te zitten. Als we deze ballon daarna tegen het plafond houden, dan blijft deze "plakken" (zie de linker onderstaande afbeelding). Dit komt doordat de negatieve ladingen in de ballon, de negatieve ladingen in het plafond wegduwen (zie de rechter afbeelding). Als gevolg blijft er netto een positieve lading achter. De ballon wordt op zijn plek gehouden door de aantrekkingskracht tussen deze positieve ladingen en de negatieve ladingen in de ballon. We spreken bij dit soort fenomenen van statische elektriciteit.

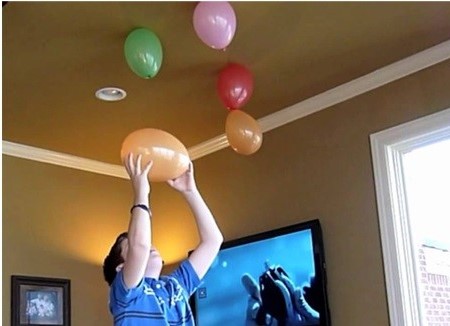
Als een voorwerp een groot overschot aan positieve ladingen heeft en een ander voorwerp een groot overschot aan negatieve ladingen, dan kan de aantrekkingskracht tussen deze ladingen zo groot worden dat de negatieve ladingen overspringen naar de positieve ladingen. We zien dan een 'vonk' overspringen (zie de onderstaande afbeelding). Het zijn meestal de negatieve elektronen die de sprong maken en niet de veel zwaardere positieve protonen.

De SI-eenheid van de hoeveelheid lading (Q) is de coulomb (C). Er geldt dus:

$$ [Q] = \text{C} $$

Eén elektron heeft een negatieve lading van:

$$ e = -1,602 \times 10^{-19} \text{ C} $$

Deze waarde is terug te vinden in BINAS tabel 7. De lading van een elektron is dus erg klein. Met een verhoudingstabel kunnen we uitrekenen hoeveel elektronen samen één coulomb aan lading vormen:

1 elektron	6,241× 10¹⁸ elektronen
-1,602 × 10^-19C	-1,000 C

Als we elektriciteit willen opwekken, dan hebben we in ieder geval een spanningsbron nodig. Een spanningsbron is een voorwerp waarvan één onderdeel een overschot aan negatieve ladingen bevat (de minpool) en een ander onderdeel een overschot aan positieve ladingen bevat (de pluspool). Voorbeelden van spanningsbronnen zijn de batterij, het stopcontact en de dynamo. Als we de twee polen met elkaar verbinden, dan spreken we van een gesloten stroomkring. Als gevolg daarvan gaan de negatieve ladingen naar de pluspool stromen. Het bewegen van deze ladingen noemen we elektriciteit.

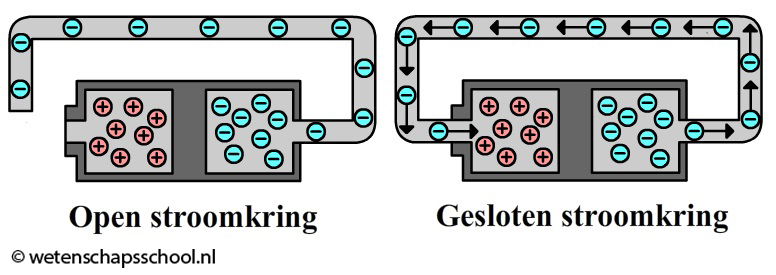
Het zijn alleen de negatieve elektronen die door de elektriciteitsdraden stromen van de min naar de plus. De positieve ladingen zitten immers goed vast in de atoomkernen. Toch zeggen we (helaas) dat de stroom van plus naar min stroomt. In werkelijkheid bewegen de elektronen dus precies de andere kant op! Deze onhandigheid stamt nog uit de tijd voordat de elektronen ontdekt waren.

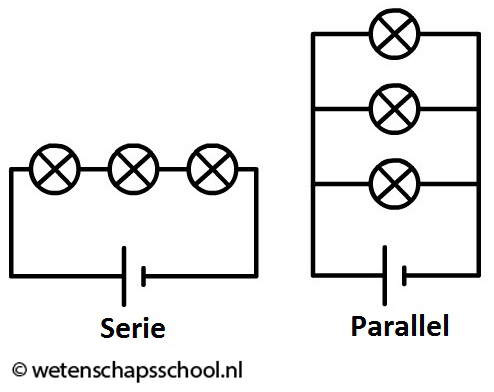
In de onderstaande afbeelding is aan de stroomkring ook een gloeilamp en een schakelaar toegevoegd. Een schakelaar is niet meer dan een klepje, waarmee de stroomkring geopend en gesloten kan worden. Alleen als de schakelaar gesloten is gaan de ladingen van de min- naar de pluspool stromen. Aan de rechterkant zien we ook een schematische weergave van deze schakeling. Zoals je ziet gebruiken we voor de lamp een cirkel met een kruis erin en voor de spanningsbron een korte en een lange streep (de lange streep is de pluspool). Als de ladingen door de schakeling stromen, dan botsen ze voortdurend tegen de atomen waaruit de schakeling bestaat. In de gloeidraad van een gloeilamp leveren deze botsingen genoeg energie om de draad zo warm te maken dat deze gaat gloeien.

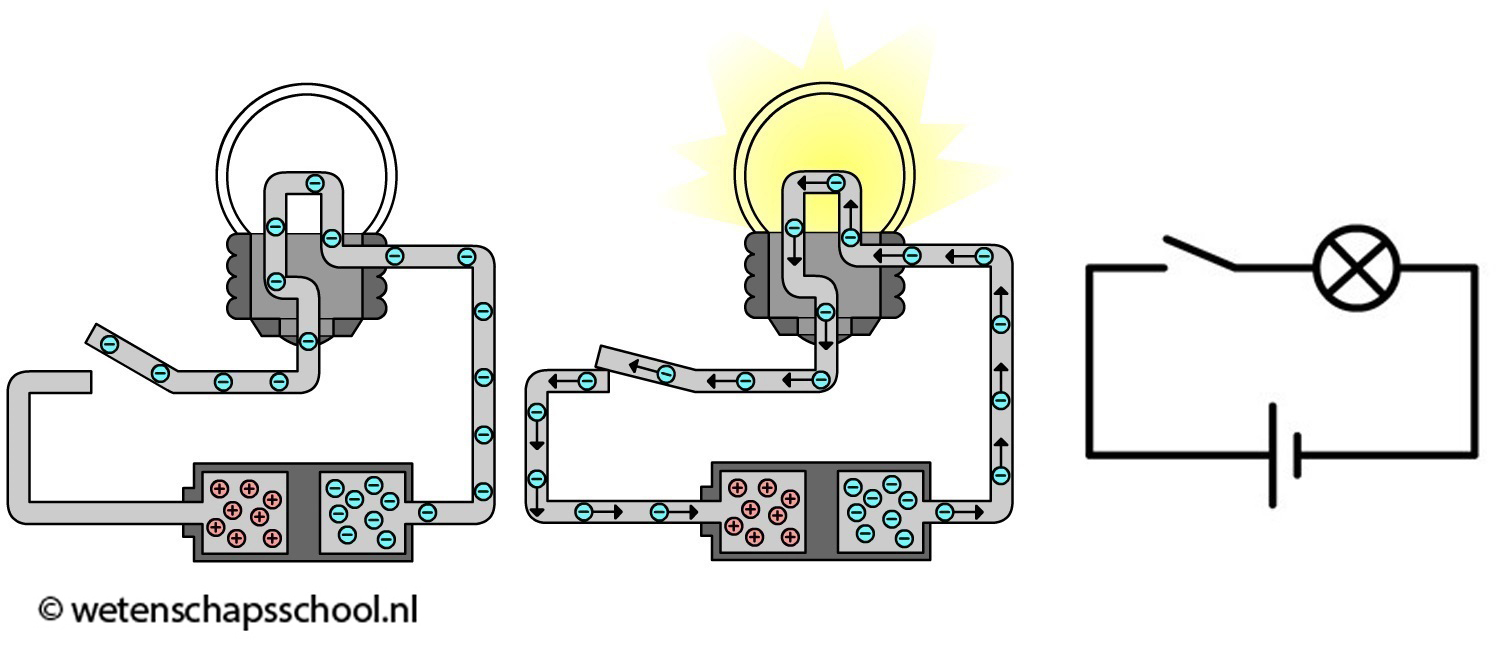
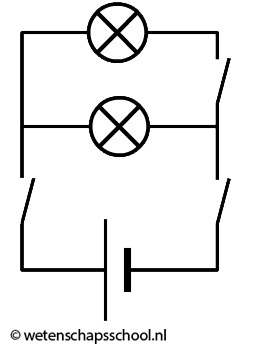
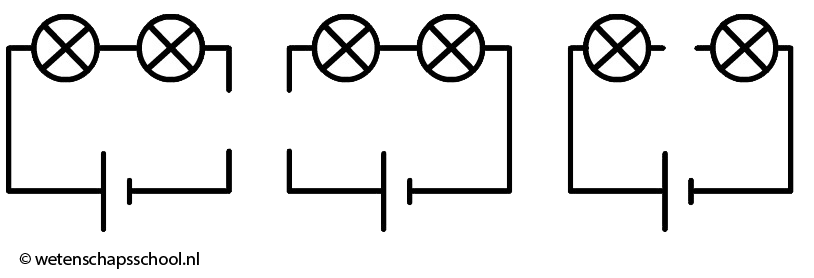
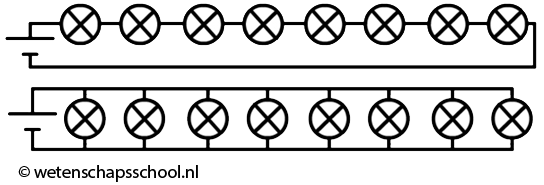
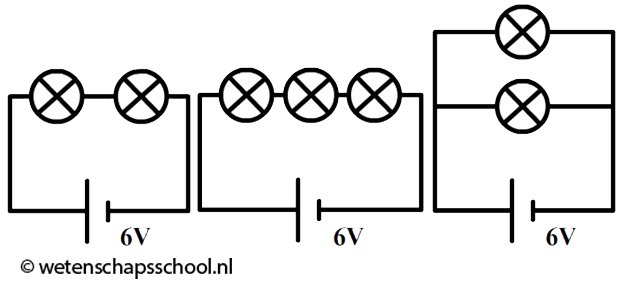
Als we meerdere lampjes op een spanningsbron aansluiten, dan kunnen we dat op verschillende manieren doen. Linksonder zien we de zogenaamde serieschakeling. In een serieschakeling zijn alle lampjes in dezelfde stroomkring opgenomen. Als we in deze schakeling één lampje losdraaien, dan wordt deze stroomkring verbroken en gaan alle lampjes uit. Rechts zien we de zogenaamde parallelschakeling. In een parallelschakeling heeft elk lampje zijn eigen stroomkring. Als we in deze schakeling één lampje losdraaien, dan wordt slechts één van de stroomkringen verbroken. De andere lampjes blijven in dit geval gewoon branden. Als er een schakeling wordt gebouwd uit meerdere lampjes en het is niet serie en niet parallel, dan noemen we dit een gemengde schakeling.

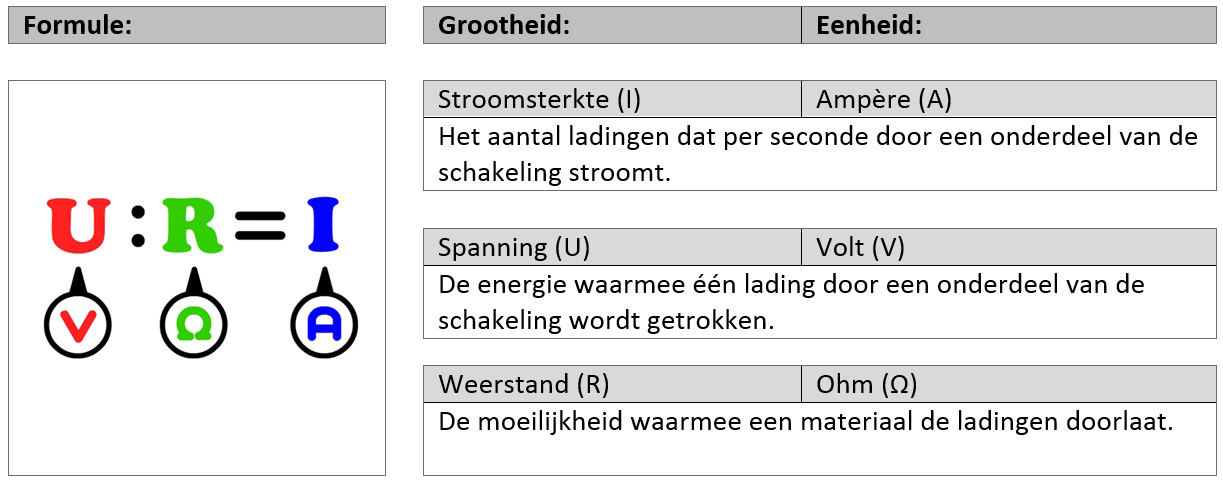
Als we elektriciteit willen begrijpen, dan spreekt het voor zich dat we willen weten hoeveel lading er in een bepaalde tijd door de schakeling stroomt. We noemen dit de stroomsterkte (I). De SI-eenheid van de stroomsterkte is de ampère (A). Ampère staat voor de hoeveelheid coulomb die per seconde door een punt in de schakeling stroomt. De ampère is dus gelijk aan coulomb per seconde (C/s). Er geldt dus:

$$ [I] = \text{A} = \text{C/s} $$

We kunnen de stroomsterkte berekenen met de volgende formule:

$$ I = \frac{Q}{t} $$

Stroomsterkte (I)

ampère (A)

Lading (Q)

coulomb (C)

Tijd (t)

seconde (s)

Als de elektronen tegen de atomen in de schakeling botsen, dan verliezen ze energie aan het materiaal. De energie die per coulomb aan lading verloren gaat noemen we de spanning (U). De SI-eenheid van de spanning is de volt (V). Volt staat voor de hoeveelheid energie in joule aan energie die door elke coulomb aan lading uitgegeven wordt. Volt is dus gelijk aan joule per coulomb (J/C). Er geldt dus:

$$ [U] = \text{V} = \text{J/C} $$

We kunnen de spanning berekenen met:

$$ U = \frac{\Delta E}{Q} $$

Spanning (U)

volt(V)

Energieverschil (ΔE)

joule (J)

Lading (Q)

coulomb (C)

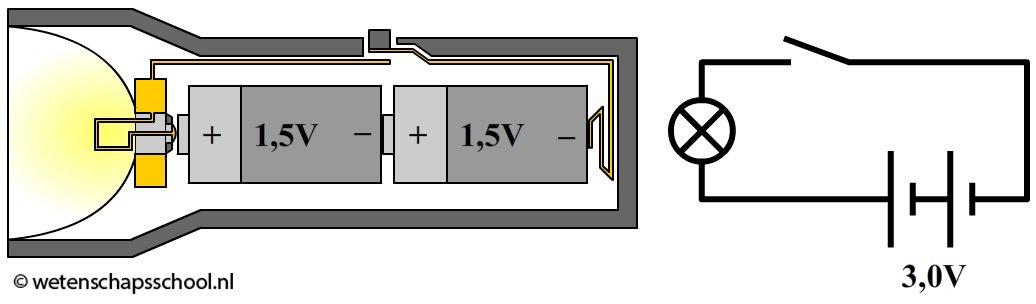
De spanningsbron geeft energie aan de ladingen. Als de spanning over de spanningsbron bijvoorbeeld 20 V is, dan krijgt elke coulomb aan lading dus 20 joule aan energie mee. De meeste spanningsbronnen hebben een vaste spanning. Over een stopcontact staat bijvoorbeeld in Nederland altijd 230 V. We noemen dit ook wel de netspanning. Een normale AA-batterij heeft een spanning van 1,5 V. We kunnen ook spanningsbronnen aan elkaar koppelen. Hieronder zien we bijvoorbeeld twee AA-batterijen die in serie gekoppeld zijn. De totale spanning wordt in dat geval 1,5 + 1,5 = 3,0 V.

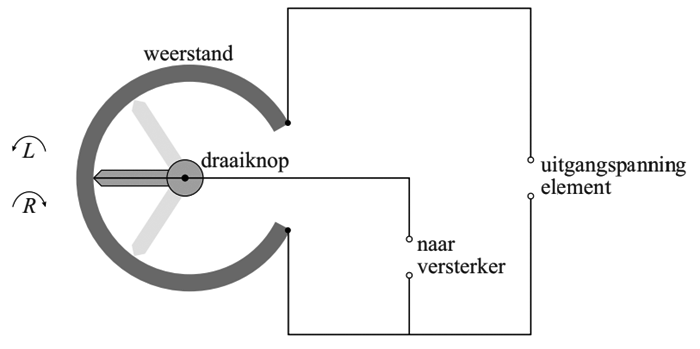
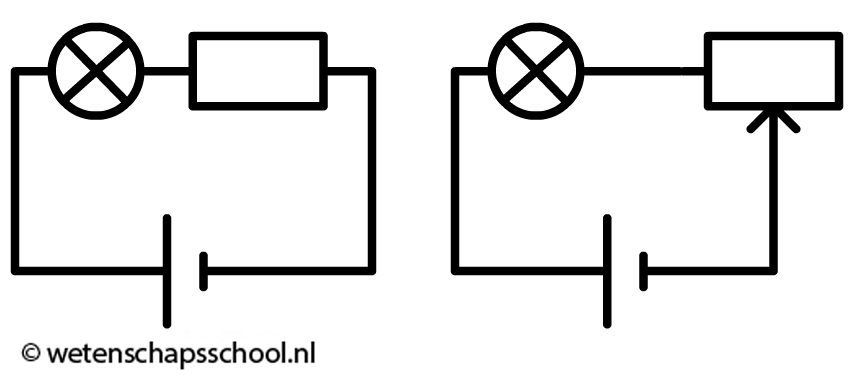
We sluiten deze paragraaf af door nog een paar andere onderdelen te noemen die je in dit hoofdstuk zal tegenkomen. Het rechthoekige symbool in de eerste onderstaande afbeelding wordt een (vaste) weerstand genoemd. Een vaste weerstand wordt gebruikt om de stroom door een draad te beperken. Een weerstand wordt bijvoorbeeld gebruikt als een lampje weinig stroom nodig heeft om te branden. Naast een vaste weerstand bestaat ook de zogenaamde variabele weerstand. De waarde van deze weerstand is handmatig in te stellen. Dit onderdeel wordt bijvoorbeeld gebruikt om een lamp handmatig te dimmen (zie de schakeling rechtsonder).

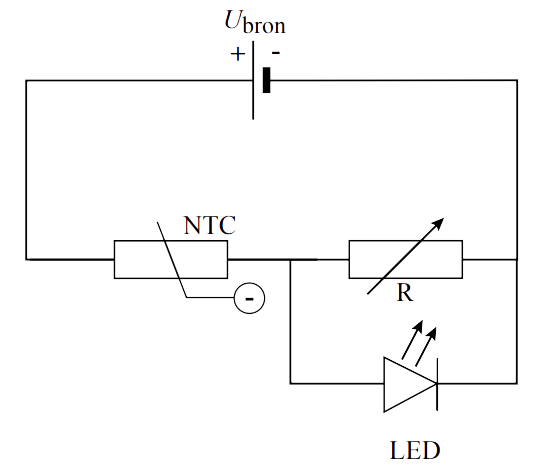
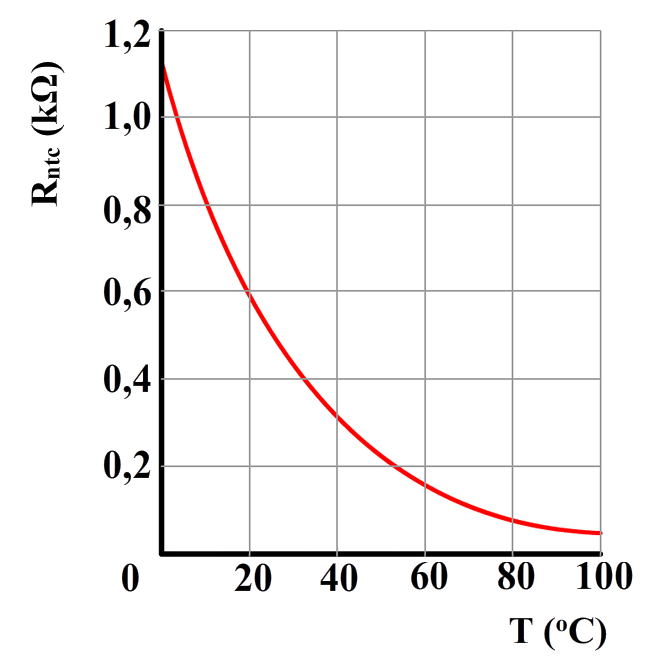
Een ander veelvoorkomend onderdeel is de NTC. De NTC is een weerstand waarvan de waarde afhangt van de temperatuur. Hoe hoger de temperatuur, hoe lager de weerstand. Een gerelateerd onderdeel is de PTC. Hier geldt: hoe hoger de temperatuur, hoe hoger de weerstand. Deze componenten worden gebruikt als temperatuursensoren. Hieronder zien we het symbool voor de NTC en de LDR. Deze en vele andere symbolen zijn te vinden in BINAS tabel 16.

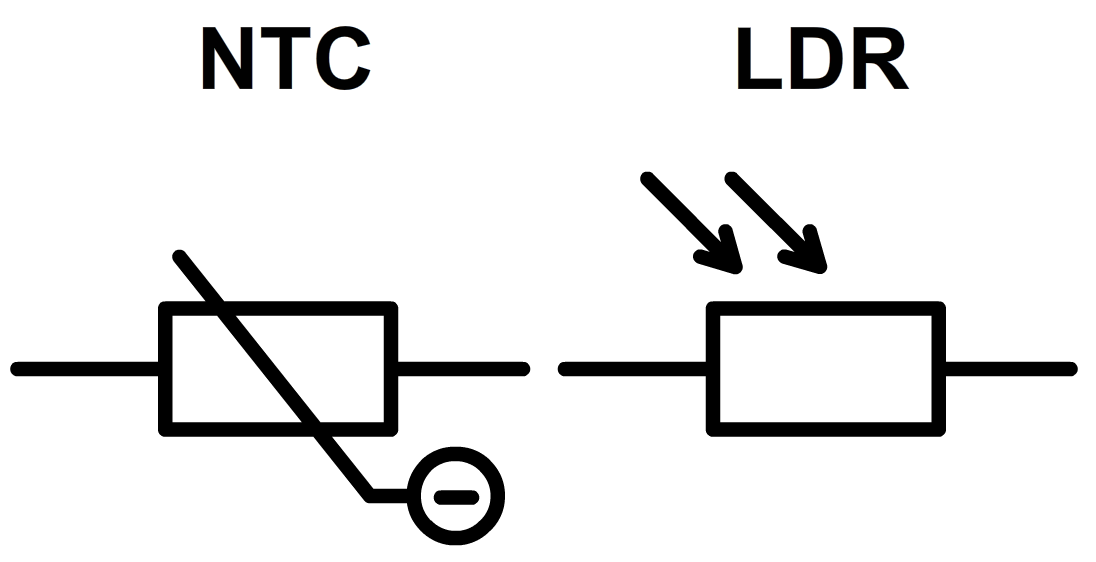
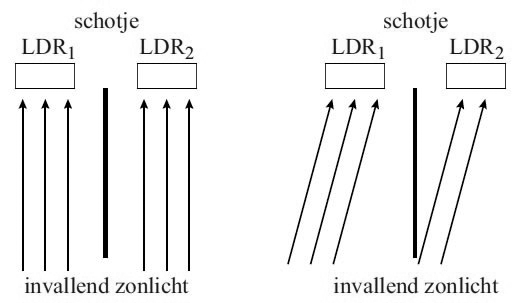
Een ander onderdeel is de LDR. Dit is een weerstand waarvan de waarde afhangt van de lichtintensiteit die erop valt. Deze component kan bijvoorbeeld gebruikt worden als lichtsensor.

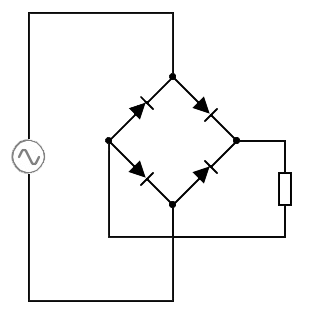
Als laatste onderdeel noemen we de diode. Een diode is een onderdeel dat stroom alleen in één richting door laat. Het symbool voor een diode is hieronder weergegeven en lijkt een beetje op een pijltje. Stroom kan alleen worden doorgelaten in de richting van dit pijltje (Let op! Dit betekent dat elektronen juist de andere kant op kunnen stromen). Een lichtgevende diode wordt ook wel een LED genoemd.

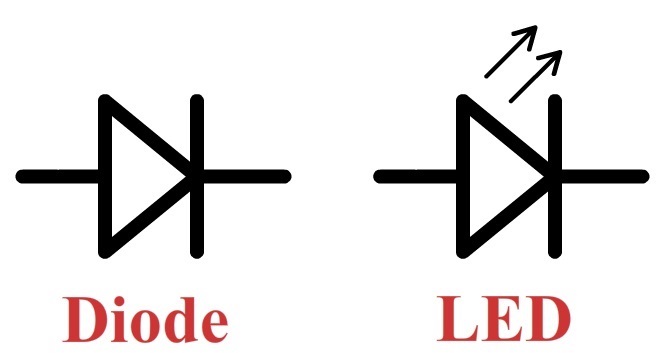
       Redeneren met lading

(2p) Leg uit of de volgende stellingen waar zijn of niet:

In een neutraal voorwerp zitten geen ladingen.

In een positief geladen voorwerp zitten geen negatieve ladingen.

Een elektroscoop bestaat uit een glazen fles met daarin een metalen staaf. Aan het einde van de staaf bevinden zich twee strookjes aluminiumfolie.

(1p) Als je de bovenkant van de elektroscoop met een negatief geladen staaf aanraakt, dan gaan de strookjes aluminium uit elkaar. Verklaar dit.

(1p) Verklaar wat er met de aluminium strookjes gebeurt als je de bovenkant met een positief geladen staaf aanraakt.

(1p) Leg ook uit wat er in deze situatie met de ladingen gebeurt.

(2p) Als je een negatief geladen ballon naast een straaltje water plaatst, dan gaat het water afbuigen. Leg met behulp van een schematische tekening van ladingen uit waarom het water afbuigt. Gebruik voor de positieve ladingen een ‘+’ en voor de negatieve ladingen een '-'

Een persoon raakt de grote positief geladen metalen bol van een Van der Graaff generator aan en als gevolg gaan haar haren overeind staan.

(2p) Leg uit of de elektronen het haar in of uit stromen.

(1p) Leg uit waarom de haren overeind gaan staan.

       Ontwerpen en begrijpen van elektrische schakelingen

(3p) In de volgende schakeling zijn drie schakelaren opgenomen. Ga voor elke schakelaar na welke lampen uitgaan als de schakelaar geopend wordt (en de andere schakelaren dicht blijven).

In de onderste schakeling zijn vier identieke lampjes opgenomen.

(3p) Ga na welke lampjes nog branden als je telkens één van de lampjes losdraait.

(1p) Lampje D brandt het felst. Verklaar waarom dit het geval is.

(1p) Geef bij elk van de volgende tekeningen aan of de lampjes wel of niet branden. Leg je keuze uit.

(1p) In een appartement in een flat bevindt zich een deurbel. De bel kan geactiveerd worden met behulp van twee schakelaren. Eén schakelaar bevindt zich bij de voordeur van het appartement en de ander bij de voordeur van de flat zelf. Teken de schakeling die hier beschreven is.

(1p) Een leerling maakt een schakeling waarmee hij kan testen of vloeistoffen wel of niet stroom geleiden. Teken deze schakeling.

(3p) Beschrijf de werking van de NTC, de LDR, de variabele weerstand en de diode.

(1p) Een persoon installeert een lamp in zijn woonkamer die hij handmatig kan dimmen. Teken deze schakeling.

(1p) Een persoon neemt een ventilator op in een schakeling. De schakeling zorgt ervoor dat de ventilator harder gaat draaien als het in de woonkamer warmer is. Teken deze schakeling

(3p) In de onderstaande afbeelding is een zogenaamde gelijkrichter afgebeeld, bestaande uit vier diodes. Een gelijkrichter zet wisselspanning om in gelijkspanning. Een wisselspanning is een spanning waarbij de plus- en de minpolen met een snel tempo omwisselen. Dit apparaat wordt bijvoorbeeld gebruikt als je een laptop aansluit op het stopcontact. Het stopcontact is een wisselspanningsbron, terwijl een laptop gelijkspanning nodig heeft.
Leg met behulp van de afbeelding uit hoe wisselspanning (links) wordt omgezet in gelijkspanning (rechts).

       Redeneren en rekenen met lading, stroomsterkte en spanning

(2p) Leg uit wat het verschil is tussen stroomsterkte en spanning.

Er stroomt 200 mA aan stroom door een stroomdraad.

(3p) Bereken hoeveel coulomb er per minuut door de draad stroomt.

(2p) Bereken hoeveel elektronen er per minuut door de draad stromen.

Er staat een spanning van 20 V over een lampje. Na 5,0 seconden is er 1,0 coulomb aan lading door de draad gestroomd.

(2p) Bereken de stroomsterkte.

(3p) Bereken hoeveel energie er per seconde door de draad stroomt.

(3p) Bereken hoeveel energie elk elektron afgeeft als het door het lampje stroomt.

Het opladen van een bepaalde mobiele telefoon via een adapter duurt 90 minuten. Op de adapter lezen we: '230 V; 0,15 A'.

(3p) Bereken hoeveel elektronen per seconde de telefoon in stromen tijdens het opladen.

(2p) Bereken hoeveel lading er tijdens het opladen in de telefoon is gestroomd.

(2p) Bereken hoeveel energie het opladen heeft gekost.

Bij een blikseminslag verplaatst zich 0,75 C aan lading in 8 ms van een wolk naar de aarde. De spanning tussen wolk en aarde is gemiddeld 75 MV.

(2p) Bereken hoeveel elektronen er verplaatst zijn.

(3p) Bereken de stroomsterkte van de blikseminslag.

(3p) Bereken hoeveel energie is vrijgekomen bij de inslag. Gebruik hiervoor het antwoord van vraag b.

§2 Stroomsterkte en spanning

In deze paragraaf gaan we de beweging van lading nader bestuderen. Dit doen we aan de hand van de begrippen stroomsterkte en spanning.

Laten we eens kijken hoe het zit met de stroomsterkte in een aantal verschillende schakelingen. In de onderstaande afbeelding zien we lading stromen door een serieschakeling. In een serieschakeling gaat alle lading door alle lampjes heen. De hoeveelheid lading die uit de spanningsbron stroomt, is dus gelijk aan de hoeveelheid lading die het rechter lampje in stroomt en even later het linker lampje in stroomt. De stroomsterkte is in een serieschakeling dus in alle onderdelen gelijk.

AFBEELDING

Hieronder zien we een parallelschakeling. In een parallelschakeling zijn er meerdere stroomkringen waarover de lading zich verdeelt. Hoe de stroomsterkte zich verdeelt hangt af van de weerstand van de lampjes. Alleen als de lampjes dezelfde weerstand hebben, zal de stroomsterkte door beide lampjes gelijk zijn.

AFBEELDING

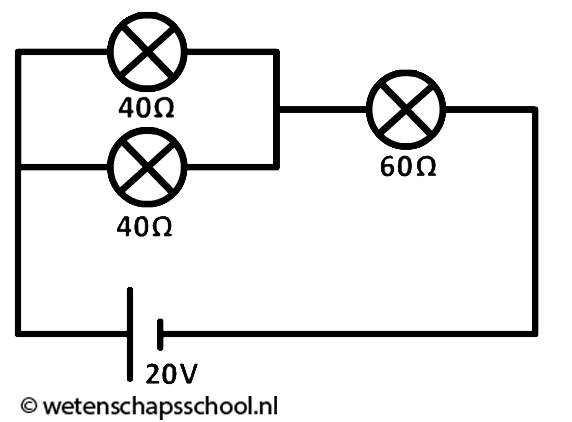
Laten we nu een gemengde schakeling bestuderen. Hieronder zien we 4 A uit de spanningsbron stromen. Al deze lading komt aan bij de rechter lamp. Hier is de stroomsterkte dus ook 4 A. Daarna splitsen de ladingen op. Stel dat 1 A bovenlangs gaat, dan weet je dat de rest (3 A) onderlangs moet gaan.

AFBEELDING

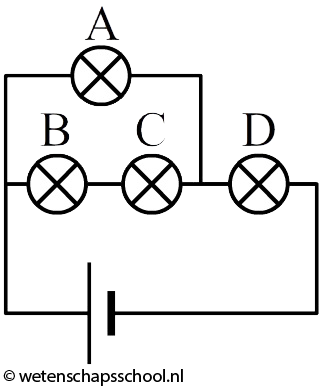
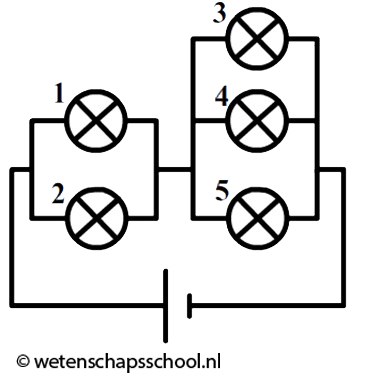
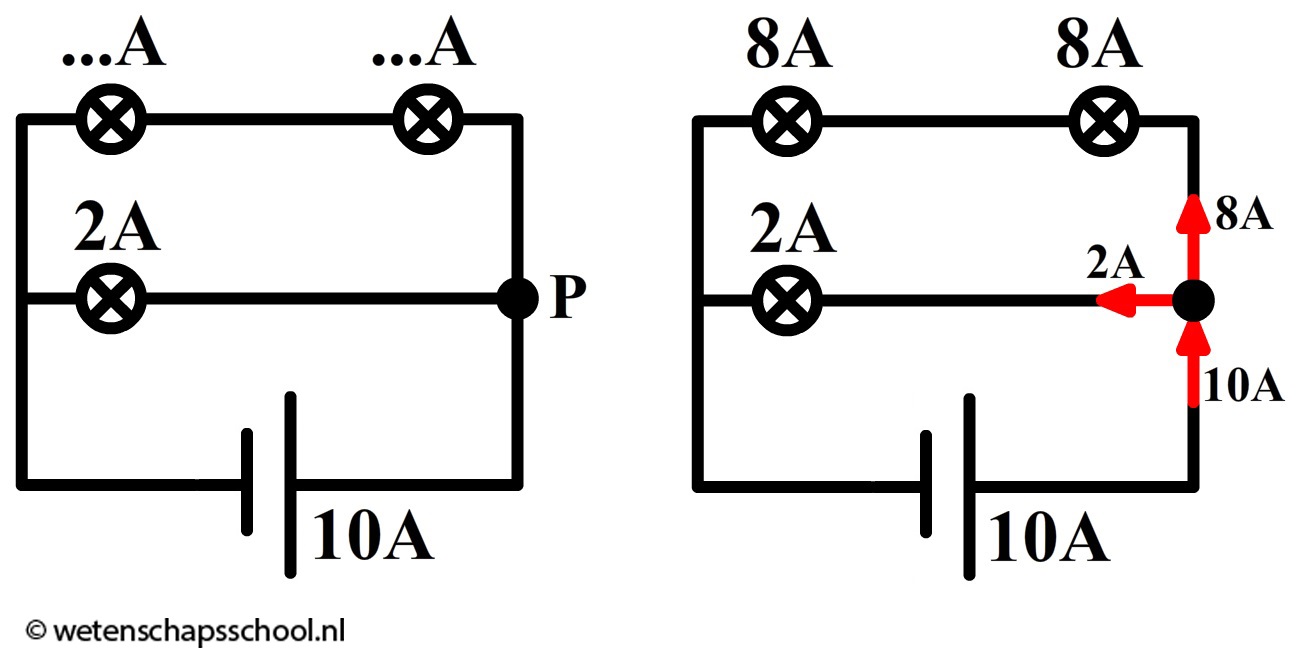
In de onderstaande afbeelding stroomt 10 A uit de spanningsbron. Bij punt P splitsen de ladingen op. Als blijkt dat 2 A linksaf gaat, dan moet de rest (8 A) dus bovenlangs gaan. Deze 8 A gaat door beide bovenstaande lampjes heen. Door elk stroomt dus 8 A.

Laten we nu de spanning bestuderen. Hieronder zien we bijvoorbeeld een serieschakeling. Stel dat de spanningsbron een spanning van 20 V heeft, dan betekent dit dat elke coulomb aan lading 20 J aan energie meekrijgt om te besteden in de schakeling. Elke lading gaat in deze schakeling door beide lampjes heen. Als gevolg moet elke lading zijn energie verdelen over de twee lampjes. De 20 V aan spanning wordt dus verdeeld over de lampjes. Hoe de spanning precies verdeeld wordt hangt af van de weerstand van de lampjes. Alleen als de lampjes dezelfde weerstand hebben, zal de spanning over beide lampjes gelijk zijn.

Rechts zien we een parallelschakeling. Hier gaat elke lading maar door één lampje heen. Elke lading besteedt dus al zijn energie in slechts één lampje. Als de spanningsbron een spanning van 20 V heeft, dan heeft in een parallelschakeling elk lampje dus ook een spanning van 20 V. Het veranderen van de weerstanden heeft hier geen invloed op.

AFBEELDINGEN

Nu tijd voor gemengde schakelingen. De onderstaande schakeling bestaat uit twee stroomkringen. Sommige ladingen gaan door de ene stroomkring en sommige ladingen gaan door de andere stroomkring. In elke stroomkring moet een coulomb aan lading in totaal 12 J kwijtraken. Als gegeven is dat over de rechter lamp een spanning van 8 V staat, dan moet over de twee linker lampen dus elk een spanning van 4 V staan. Op deze manier wordt in elke stroomkring 12 J aan energie besteed. Voor elke stroomkring geldt dus dat de spanning van de spanningsbron gelijk is aan de spanning van de onderdelen in deze stroomkring tezamen.

AFBEELDINGEN

Rekenen met stroomsterkte en spanning in gemengde schakelingen

Ga naar deze opdracht op de website of maak het stencil aan het eind van de paragraaf.

Klik op de lampjes en de spanningsbron en vul de juiste stroomsterkte en spanning in:

(2p) Twee dezelfde lampjes zijn in serie aangesloten op een batterij. De batterij levert een stroomsterkte van 250 mA. Leg uit hoe groot de stroomsterkte door elk van de lampjes is. Gebruik in je antwoord het 'lading'.

(3p) Twee dezelfde lampjes zijn parallel aangesloten op een batterij. De batterij levert een stroomsterkte van 0,090 A. Leg uit hoe groot de stroomsterkte door elk van de lampjes is. Gebruik in je antwoord het woord 'lading'.

Verklaar de volgende correcte uitspraken. Gebruik in je antwoord in beide gevallen het woord 'energie'.

(2p) De spanning is overal gelijk in een parallelschakeling.

(2p) De spanning wordt verdeeld over de lampjes in een serieschakeling.

Hieronder zien we twee schakelingen met een aantal dezelfde lampjes:

(1p) Beschrijf wat er gebeurt als een lampje in de bovenste schakeling doorbrandt.

(1p) Beschrijf wat er gebeurt als een lampje in de onderste schakeling doorbrandt.

(1p) Leg uit of de spanning over de lampjes verandert als we een lampje uit de onderste schakeling verwijderen.

In de volgende schakeling zijn vijf dezelfde lampjes opgenomen.

(1p) Door welke lampjes in de bovenstaande schakeling is de stroomsterkte het grootst? Leg je keuze uit.

(1p) Door lampje 1 en 2 stroomt elk 750 mA. Bereken de totale stroomsterkte die de spanningsbron levert.

(1p) Bereken de stroomsterkte door lamp 3.

(2p) Over lampje 1 en 2 staat elk een spanning van 6,0 V en over lampjes 3, 4 en 5 staat elk een spanning van 4,0 V. Bereken de spanning over de spanningsbron.

(4p) Noteer bij elk onderdeel in de onderstaande schakeling de spanning en de stroomsterkte:

(2p) In een koplamp van een fiets zitten zes lampjes, die ieder op een spanning van 1,0 V branden. De spanning wordt geleverd door twee batterijen, die ieder een spanning leveren van 1,5 V. Teken de schakeling die hier beschreven is.

(VWO) In de onderstaande schakeling zijn vijf weerstanden opgenomen.

(4p) Bereken voor elk van de horizontaal afgebeelde weerstanden de spanning.

(6p) Er zijn twee stroomkringen die door de middelste verticale weerstand lopen. Bereken de spanning over deze weerstand. Geef ook aan in welke richting de stroom door deze weerstand loopt.

§3 De Wet van Ohm

Als we de spanning en de stroomsterkte van een onderdeel in een schakeling kennen, dan kunnen we hiermee de weerstand uitrekenen. We doen dit met de zogenaamde wet van Ohm. Ook gaan we leren rekenen met vermogen en energie. We gebruiken als eenheid voor de energie zowel joule als kilowattuur.

De weerstand (R) van een onderdeel in een schakeling kunnen we berekenen met de wet van Ohm:

$$ R = \frac{U}{I} $$

Spanning (U)

volt (V)

Weerstand (R)

ohm (Ω)

Stroomsterkte (I)

ampère (A)

Deze wet werkt trouwens niet voor de spanningsbron zelf. De (ideale) spanningsbron heeft namelijk helemaal geen weerstand.

Voorbeeld

Vraag:

Twee dezelfde lampjes in serie worden aangesloten op de netspanning. De stroomsterkte die de spanningsbron levert is gelijk aan 150 mA. Bereken de weerstand van elk van de lampjes.

Antwoord:

In een serieschakeling weten we dat de stroomsterkte overal gelijk is. Voor elk lampje geldt dus een stroomsterkte van 150 mA. Dit is gelijk aan 150 / 1000 = 0,150 A.

Ook weten we dat de lampjes zijn aangesloten op de netspanning. De netspanning is in Nederland altijd gelijk aan 230 V. In een serieschakeling verdeelt deze spanning zich over de lampjes. Omdat het hier om twee dezelfde lampjes gaat, weten we dat de spanning zich gelijk zal verdelen. Over elk lampje staat dus een spanning van 230 / 2 = 115 V.

Met deze gegevens kunnen we met de wet van Ohm de weerstand bepalen. Voor elk lampje geldt:
$$ R = \frac{U}{I}=\frac{115}{0,150}= 767 \text{ }Ω $$

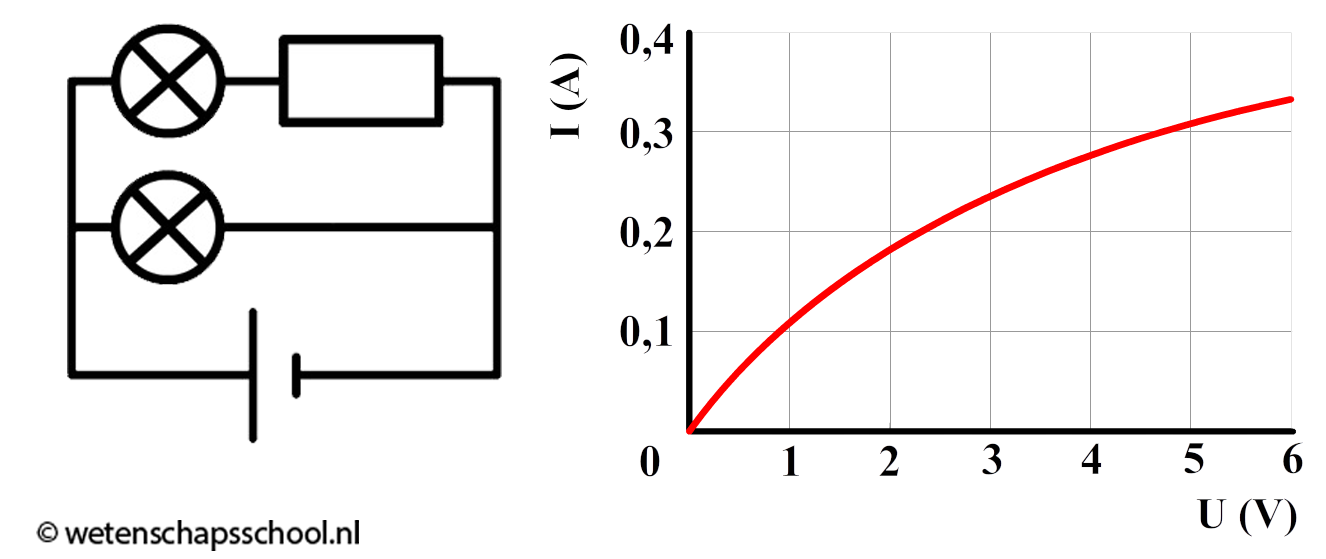
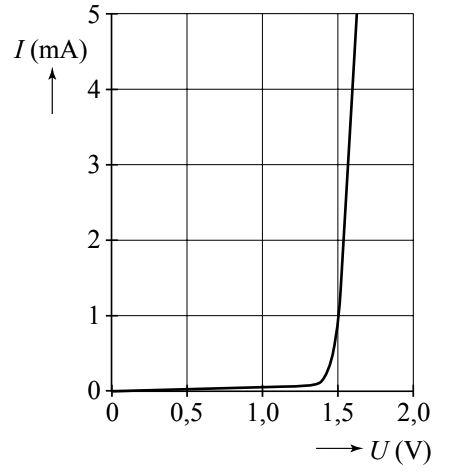
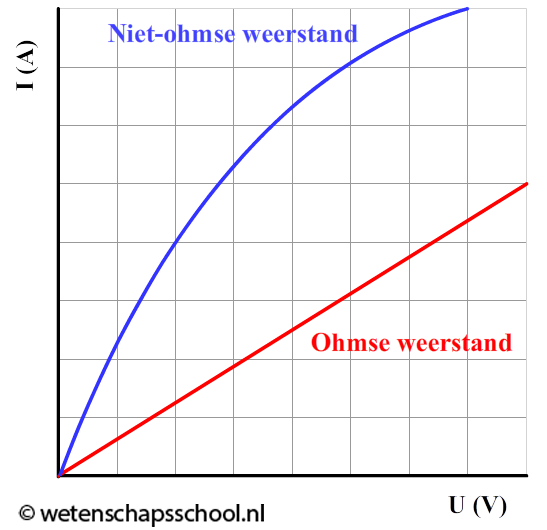
Een onderdeel in een schakeling wordt een ohmse weerstand genoemd als het een vaste weerstand heeft. Of een onderdeel een ohmse weerstand heeft, is gemakkelijk te herkennen aan het (I,U)-diagram (zie het onderstaande diagram). De grafiek voor een ohmse weerstand is hier altijd een rechte lijn door de oorsprong (we spreken hier van een recht evenredig verband).

Als we de pluspool en de minpool direct verbinden met een materiaal met een erg kleine weerstand, dan ontstaat er kortsluiting. Aan de bovenstaande formule kan je zien dat een kleine weerstand zorgt voor een grote stroomsterkte. Deze grote hoeveelheid stroom is niet alleen gevaarlijk voor het menselijk lichaam, maar kan ook gemakkelijk een brand veroorzaken. Om ons hiertegen te beschermen bevat de meterkast een aantal zekeringen. Een simpele zekering bestaat uit een draadje dat doorbrandt als de stroomsterkte boven een bepaalde waarde uitkomt. In de rechter afbeelding zien we bijvoorbeeld een zekering die bij 20 A doorbrandt. De stopcontacten in huis zijn opgedeeld in een aantal groepen, elk met een eigen zekering. Een zekering kan ook doorbranden als je te veel apparaten tegelijk aansluit op één groep. In dit geval spreken we van overbelasting.

Voorbeeld

Vraag:

Als we een schakeling ombouwen, dan blijven over het algemeen slechts twee waarden gelijk:

De spanning van de spanningsbron

De waarde van de ohmse weerstanden

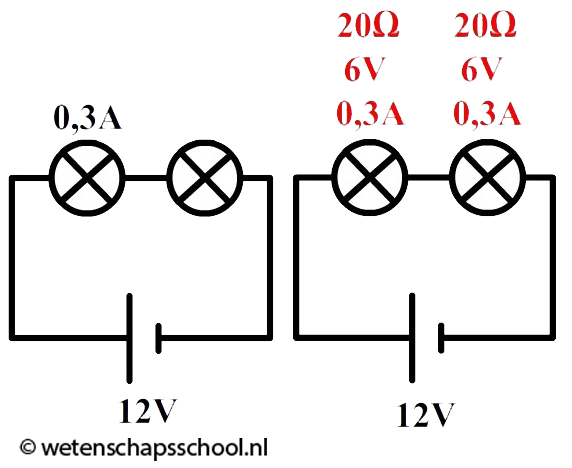
Een leerling maakt een serieschakeling bestaande uit twee dezelfde ohmse lampjes. De spanning over de spanningsbron is 12 V. De spanningsbron levert in dat geval een stroomsterkte van 0,30 A. Daarna bouwt de leerling deze schakeling om tot een parallelschakeling. Bereken hoeveel stroom de spanningsbron nu levert.

Antwoord:

De spanning van de spanningsbron is al bekend, maar de weerstand van de lampjes niet. Laten we dit eerst uitrekenen. Omdat de lampjes hetzelfde zijn, weten we dat de spanning in de schakeling eerlijk verdeeld wordt. Over beide lampjes staat dus een spanning 6,0 V. De stroomsterkte is in een serieschakeling overal gelijk. De stroomsterkte door elk lampje is dus ook 0,30 A. Met deze gegevens kunnen we de weerstand van de lampjes uitrekenen:
$$ R = \frac{U}{I}=\frac{6,0}{0,30} = 20 \Omega $$

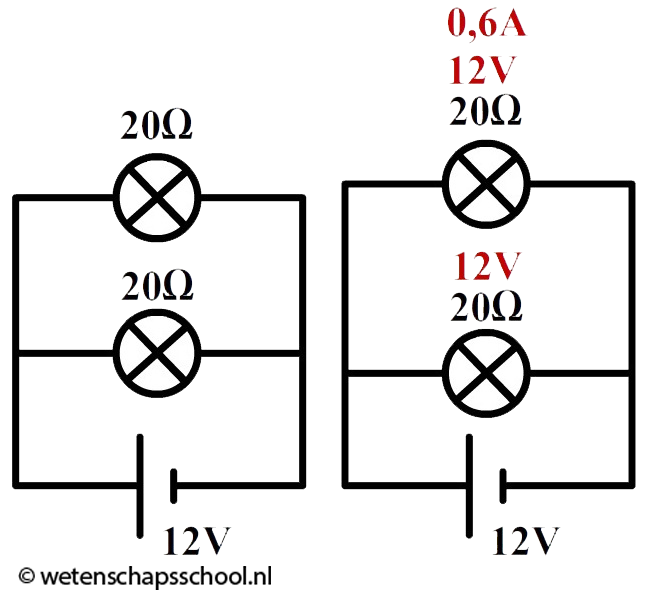
Nu veranderen we de schakeling in een parallelschakeling. Zoals eerder is opgemerkt blijven alleen de spanning van de spanningsbron en de waarde van de ohmse weerstanden gelijk (zie de linker onderstaande schakeling).

In een parallelschakeling is de spanning overal gelijk, dus over elk lampje staat nu een spanning van 12 V. Met deze gegevens kunnen we de stroomsterkte door de lampjes uitrekenen:
$$ I = \frac{U}{R}=\frac{12}{20} = 0,60 \text{ A} $$
De spanningbron levert dus een stroomsterkte van: 0,60 + 0,60 = 1,20 A.

Het vermogen (P) vertelt ons hoeveel energie een onderdeel per tijdseenheid gebruikt. De SI-eenheid van het vermogen is de watt (W) en dit gelijk aan de hoeveelheid joule per seconde. Voor het vermogen geldt dus:

$$ [P] = W = J/s $$

Voor het vermogen geldt:

$$ P = U \times I $$ $$ P = I^2R $$

Vermogen (P)

watt (W)

Spanning (U)

volt (V)

Stroomsterkte (I)

ampère (A)

Weerstand (R)

ohm (Ω)

Met behulp van het vermogen kunnen we ook de totale energie (E) uitrekenen die een component gebruikt heeft. Er geldt:

$$ P = \frac{\Delta E}{\Delta t} $$

Vermogen (P)

watt (W)

Tijdsduur (Δt)

seconde (s)

Verbruikte energie (ΔE)

joule (J)

Naast de joule is het ook mogelijk om als eenheid voor de energie de kilowattuur (kWh) te gebruiken. In dat geval moeten we het vermogen in kilowatt (kW) invoeren en de tijd in uren (h):

$$ P = \frac{\Delta E}{\Delta t} $$

Vermogen (P)

kilowatt (kW)

Tijdsduur (Δt)

uur (h)

Verbruikte energie (ΔE)

kilowattuur (kWh)

Merk op dat kilowattuur niet hetzelfde is als 'kilowatt per uur'. Kilowattuur is net als joule gewoon een maat voor de energie.

We kunnen kWh en joule als volgt omrekenen:

$$ 1 \text{ kWh} = 3\, 600 \,000 \text{ J} = 3,6 \times 10^6 \text{ J} $$

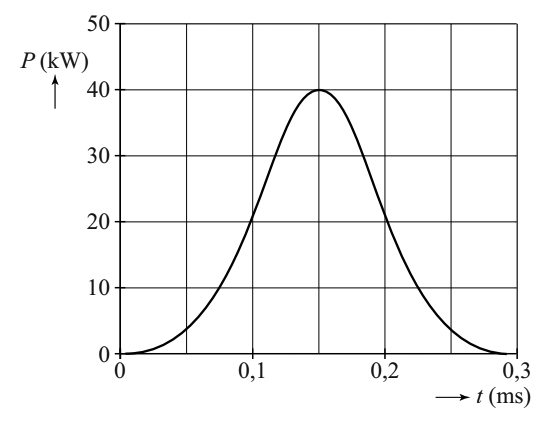
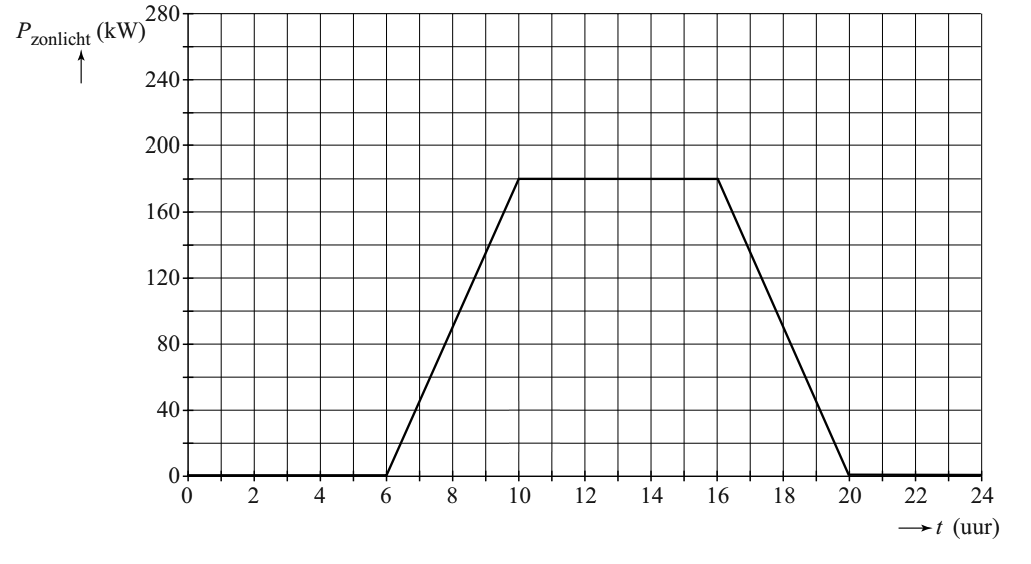
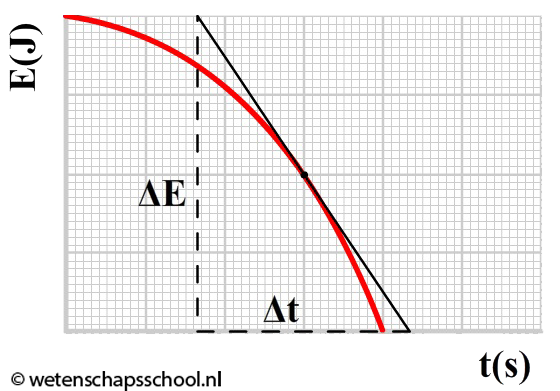
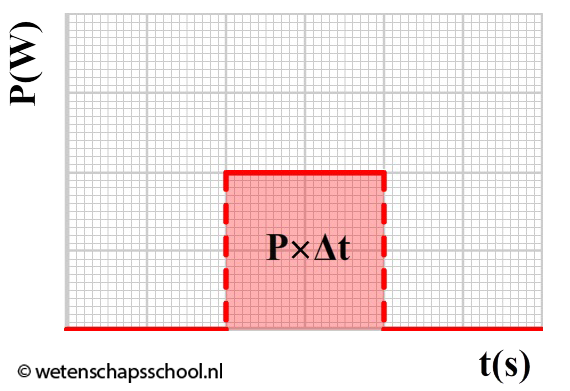
Hieronder zien we links een (E,t)-diagram. Als we de raaklijn nemen op een punt, dan is de helling van deze lijn gelijk aan ΔE/Δt. Volgens de bovenstaande formule is dit gelijk aan het vermogen (P). De raaklijn in een (E,t)-diagram is dus gelijk aan het vermogen. Rechts zien we een (P,t)-diagram. Het oppervlak onder de grafiek is gelijk aan P×Δt. Dit is volgende de bovenstaande formule gelijk aan ΔE. Het oppervlak onder een (P,t)-diagram geeft ons dus de toename (of afname) van de energie.

       Rekenen met de wet van Ohm

Ga naar deze opdracht op de website of maak het stencil aan het eind van de paragraaf.

Klik op de lampjes en de spanningsbron en vul de juiste stroomsterkte en spanning in. Voor de Ω kan je de letter 'o' gebruiken.

Een lamp met een weerstand van 200 Ω wordt op de netspanning aangesloten.

(3p) Bereken de stroomsterkte door de lamp.

(2p) Er ontstaat kortsluiting in de koperen bedrading van deze lamp. De weerstand van de bedrading is 0,01 Ω. Als de stroomsterkte in huis boven de 20 A komt, dan wordt de stroom voor de veiligheid meteen afgesloten. Bereken of een zekering van 20 A in dit geval zal doorbranden.

(7p) Een leerling maakt de onderstaande schakeling bestaande uit twee dezelfde lampjes en een vaste weerstand. Bij de lampjes hoort het (I,U)-diagram dat ook hieronder is afgebeeld. Over de spanningsbron blijkt een spanning te staan van 5,0 V. De stroomsterkte van de spanningsbron blijkt 420 mA te zijn. Bereken de waarde van de vaste weerstand.

(VWO, 5p) De onderstaande schakeling bestaat uit een variabele weerstand en een lampje. Op het lampje staat: '6,0 V; 0,50 A'. Bereken de waarde die de linkerkant van de variabele weerstand moet hebben om het lampje met de aangegeven waarde te laten branden.

(VWO) Van twee verschillende gloeilampen, genaamde W en K, is een (I,U)-karakteristiek gemeten. Hieronder zien we het resultaat. De lampen zijn in serie aangesloten op een spanningsbron van 235 V.

(2p) Bepaal met behulp van het diagram de stroomsterkte in de lampen.

(2p) Bepaal wanneer lamp W een weerstand van 500 Ω heeft.
(bron: examen HAVO 2005-1)

In een vissenkom zit een waarschuwingssysteem waarbij een LED gaat branden als de temperatuur 20 ^°C of hoger is. De schakeling van dit systeem is hieronder weergegeven. De schakeling bevat een spanningsbron van 5,0 V, een variabele weerstand, een NTC en een LED.
In de twee onderstaande grafieken zien we links hoe de weerstand van de NTC afhangt van de temperatuur en rechts zien we hoe de spanning en de stroomsterkte van elkaar afhangen bij de LED. De LED geeft licht als er ten minste 1,0 mA doorheen stroomt.

(2p) Leg uit dat de LED niet brandt bij een lage temperatuur en wel brandt bij een hoge temperatuur.

(6p) De variabele weerstand wordt zo ingesteld dat de LED licht geeft bij een temperatuur van 20^°C of hoger. Bepaal de waarde waarop de variabele weerstand is ingesteld.
(bron: examen VWO 2010-2)

       Rekenen aan schakelingen waar een aanpassing aan gemaakt wordt

(5p) Een leerling sluit 3 dezelfde vaste weerstanden in serie aan op een spanningsbron. Over de spanningsbron staat een spanning van 12 V en de bron levert een stroomsterkte van 150 mA. Dan bouwt de leerling de schakeling om tot een parallelschakeling. Bereken de stroomsterkte die de spanningsbron in dit geval levert.

De meeste auto's hebben een achterruitverwarming. Hieronder zien we een schakeling waarin een achterruitverwarming is opgenomen. De schakeling bestaat uit een aantal dunne draden en een accu met een spanning van 12 V. De accu levert een stroomsterkte van 100 mA.

(1p) Leg uit of dit een serie- of een parallelschakeling is.

(4p) Bereken de weerstand van één draadje van de verwarming.

(1p) Eén van de verwarmingsdraden brandt door. Leg uit wat het effect hiervan is op de spanning over de accu.

(3p) Leg ook uit of de stroomsterkte die de accu levert hierdoor toeneemt, afneemt of gelijk blijft. Je mag er vanuit gaan dat de draden bij benadering een ohmse weerstand hebben.
(bron: examen HAVO 2006-1)

       Rekenen en redeneren met P = UI

(2p) Laat met behulp van de formule P = UI en een eenheidsbepaling zien dat de eenheid van het vermogen gelijk is aan J/s.

(2p) Leid de formule P = I²R af met behulp van andere formules uit de paragraaf.

(1p) Twee dezelfde lampen worden aangesloten in twee verschillende schakelingen. Leg uit welke grootheid je nodig hebt als je wilt weten welke lamp de grootste lichtintensiteit heeft.

(4p) Een gloeilamp van 60 W wordt op de netspanning aangesloten. Bereken de weerstand van de gloeilamp.

(5p) Op een lamp staat: '6,0 V; 1,5 W'. Dit zijn de waarden waarbij de lamp optimaal brandt. Je wilt de lamp aansluiten op een spanningbron van 24 V. Om te voorkomen dat de lamp te fel gaat branden, sluit je een extra weerstand in serie aan op de spanningsbron. Bereken de grootte van deze extra weerstand.

(6p) Hieronder zien we drie schakelingen. In elke schakeling wordt hetzelfde type lampje gebruikt. Leg uit in welke schakeling de lampjes het felst branden en in welke het minst fel.

(2p) In de VS is de netspanning twee keer zo klein als in Nederland. Stel je sluit dezelfde lamp aan in de VS en in Nederland. Bereken welke factor het vermogen kleiner is in de VS.

Op een batterij staat: '1,5 V; 2300 mAh'. Dat betekent dat de batterij bij een spanning van 1,5 V gedurende één uur een stroom van 2,3 A kan leveren, of gedurende een half uur een stroom van 4,6 A enz.

(3p) Bereken hoeveel elektrische energie de batterij kan leveren.

(4p) De batterij wordt gebruikt in een klok met een weerstand van 12 kΩ. Bereken hoeveel jaar de klok op de batterij kan lopen.

(VWO) De elektromotoren van treinen in Nederland krijgen hun stroom via een koperen bovenleiding en de stroom wordt teruggevoerd via de rails. De bovenleiding heeft een weerstand van 0,068 Ω per kilometer. De weerstand van de rails is te verwaarlozen. De bovenleiding en de rails zijn aangesloten op een spanningsbron met een gelijkspanning van 1500 V.

Op een bepaald moment bevindt een trein zich op een afstand van 2,0 km van de spanningsbron (zie afbeelding). Op dat moment loopt er een stroom van 4,0 kA door de elektromotor van de trein.

(4p) Bereken het vermogen van de motor.

(2p) Bereken hoeveel energie er elke seconde verloren gaat in de bovenleiding.

(3p) Het energieverlies in de bovenleiding willen we natuurlijk zo veel mogelijk beperken. Om dit voor elkaar te krijgen wil het openbaar vervoer in de toekomst overstappen op een spanningsbron van 25 kV. De spanning over de elektromotor zal hierdoor ook flink toenemen. Leg uit dat er op deze manier inderdaad minder energie verloren gaat in de bovenleiding.

(bron: examen VWO 2011-1)

       Rekenen met P = ΔE/Δt

(4p) Een lamp wordt aangesloten op een batterij met een spanning van 1,5 V. De weerstand van de lamp is 30 Ω. Bereken hoeveel energie er per minuut in de lamp verbruikt wordt.

(6p) In de onderstaande afbeelding zijn twee weerstanden op een spanningsbron aangesloten. Bereken hoeveel energie de spanningsbron in een halve minuut verbruikt.

(4p) Om weilanden af te rasteren wordt vaak schrikdraad gebruikt. In het onderstaande (P,t)-diagram is het verloop van een schok van dit schrikdraad weergegeven. Volgens de wet mag de energie van één puls niet groter zijn dan 6 J. Toon aan dat deze puls aan de wet voldoet.

(bron: examen VWO 2015-1)

De Solar Impulse is een eenpersoons vliegtuig dat zonne-energie gebruikt om te vliegen. De ontwerpers hebben het vliegtuig in 2011 een volledige vlucht rond de wereld laten maken. Het vliegtuig vloog op een hoogte van 10 km boven de evenaar met een gemiddelde snelheid van 70 km/h.

(2p) Opvallend zijn de lange vleugels die vrijwel helemaal bedekt zijn met zonnecellen. Deze zonnecellen zetten de energie van het zonlicht om in elektrische energie, waarmee accu's worden opgeladen. De accu's leveren vervolgens de energie aan de motoren. Energieverliezen bij het op- en ontladen van de accu worden in deze opgave verwaarloosd. Hieronder zien we dit proces samengevat:
Het rendement van de zonnecellen is 20% en het rendement van de motoren is 60%. De motoren leveren een gemiddeld nuttig vermogen van 8,5 kW. Wat is het vermogen dat de zon moet leveren aan de zonnecellen om op dit vermogen te kunnen werken.

(2p) Het vliegtuig moet ook 's nachts kunnen vliegen. Veronderstel dat de accu's helemaal vol zijn als de nacht begint. De maximale energie-inhoud van de accu's samen is 110 kWh. Bereken hoelang de accu's energie kunnen leveren aan de motoren.

(2p) Hieronder is weergeven hoe het vermogen van het invallend zonlicht op de zonnecellen verloopt tijdens 24 uur.
Bepaal de hoeveelheid energie die de zonnecellen binnenkrijgen tijdens deze 24 uur.

(3p) Is dit genoeg om het vliegtuig 24 uur te laten vliegen?
(bron: examen HAVO 2013-2)

       Rekenen met joule en kilowattuur

(2p) Leg uit wat er niet klopt aan de volgende uitspraken:

'Een waterkoker zet per seconde 2000 W om'.

'Een lamp heeft een vermogen van 10 W. In een minuut is het vermogen dus toegenomen tot 10 × 60 = 600 W'.

(3p) Reken de volgende waarden om:

7 kWh = ... J

1500 J = ... kWh

2550 J = ... Wh

(5p) Een wasmachine met een vermogen van 1500 W draait 2,0 uur. Bereken hoeveel elektrische energie de wasmachine in die periode verbruikt in kWh en in joule.

(5p) Een lampje is aangesloten op een spanningsbron van 6,0 V. Door het lampje gaat een stroomsterkte van 0,30 A. De kWh-prijs is 0,14 euro. Bereken hoeveel het kost om het lampje 4,0 dagen te laten branden.

(7p) Een gloeilamp van 75 W kost 0,90 euro en gaat 1000 uur mee. Een spaarlamp van 15 W geeft evenveel licht, kost 7,00 euro en gaat 8000 uur mee. De kWh-prijs is 0,15 euro. Bereken hoeveel euro je bespaart in 8000 uur als je een gloeilamp vervangt door een spaarlamp.

(5p) Een leerling föhnt haar haar tweehonderd keer per jaar met een föhn van 800 W. Elke behandeling duurt 6 minuten. Bereken de kosten per jaar. Ga ervan uit dat de kWh-prijs 0,20 euro is.

§4 Stroom- en spanningsmeters

In deze paragraaf gaan we leren hoe we de spanning en de stroomsterkte kunnen meten.

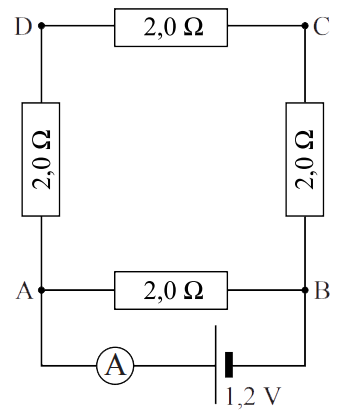
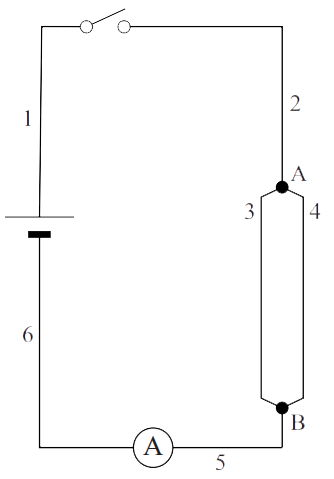
De stroomsterkte kunnen we meten met een zogenaamde ampèremeter (ook wel stroommeter genoemd). De ampèremeter sluit je in serie aan naast het onderdeel waarvan je de stroomsterkte wilt meten. Hieronder kan je zien hoe dit werkt. Aan één kant van het onderdeel haal je de draad of de draden los en dan stop je de ampèremeter hiertussen. Merk op dat de pluspool van de spanningsbron verbonden is met de pluspoort van de ampèremeter en de minpool met de minpoort.

AFBEELDING

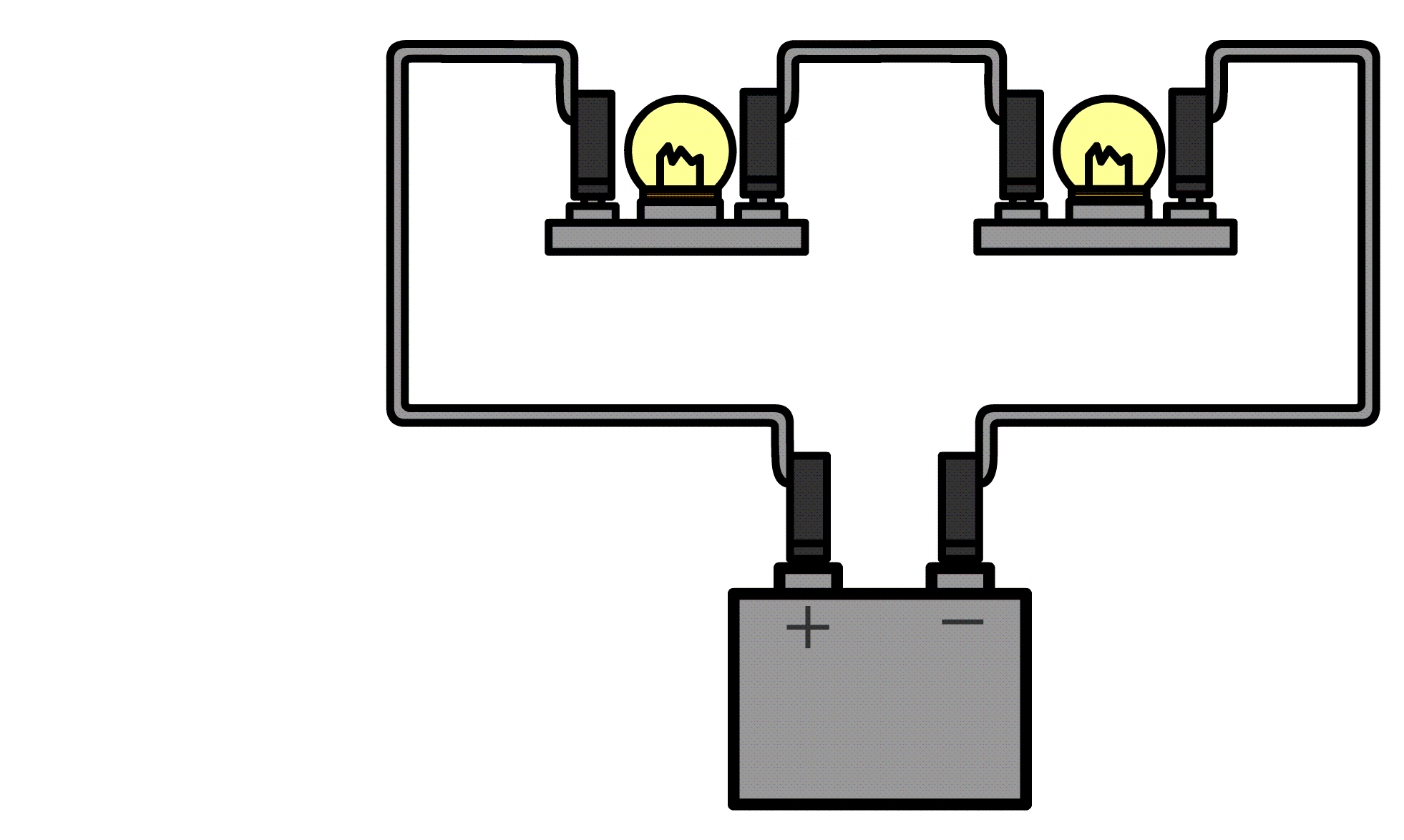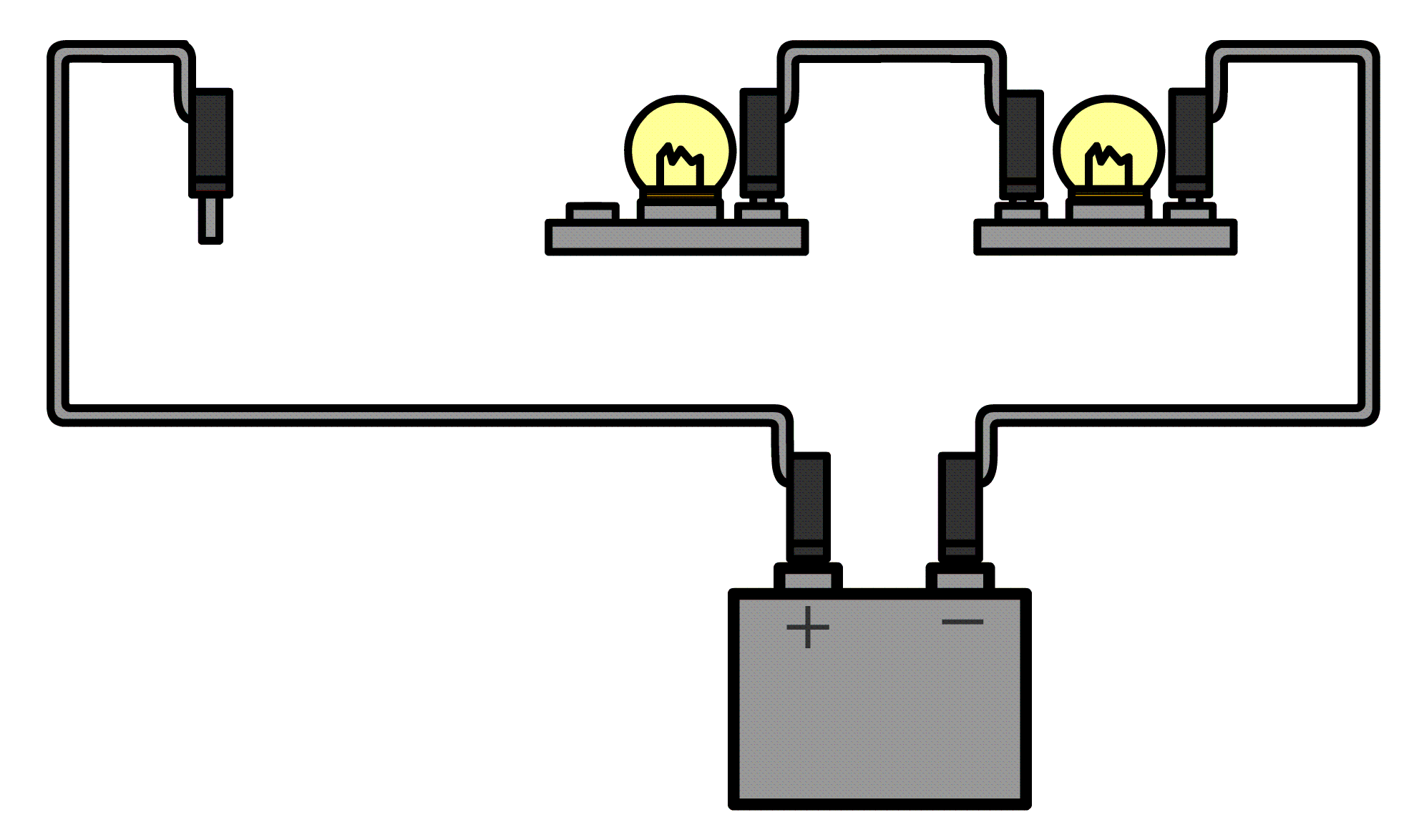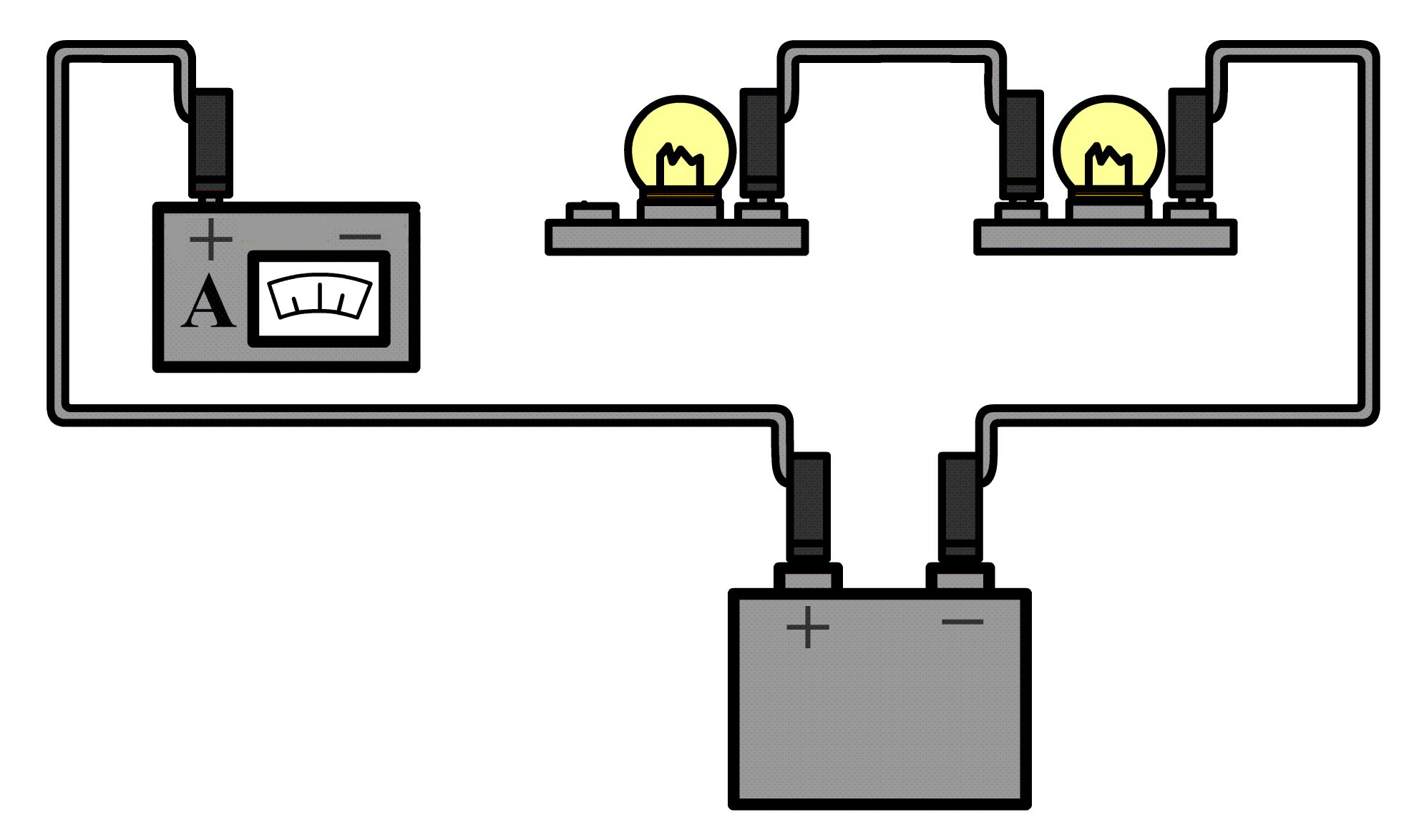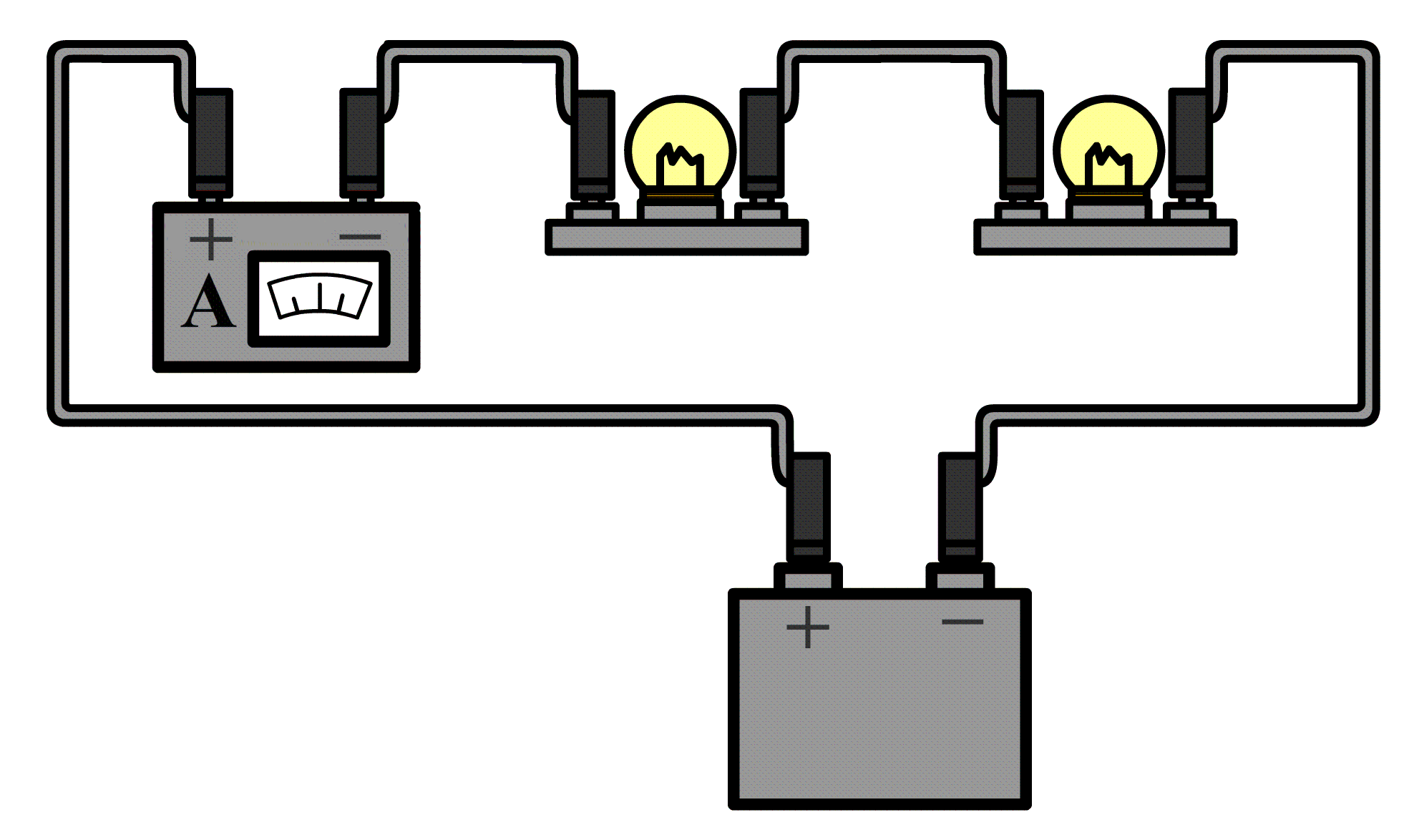
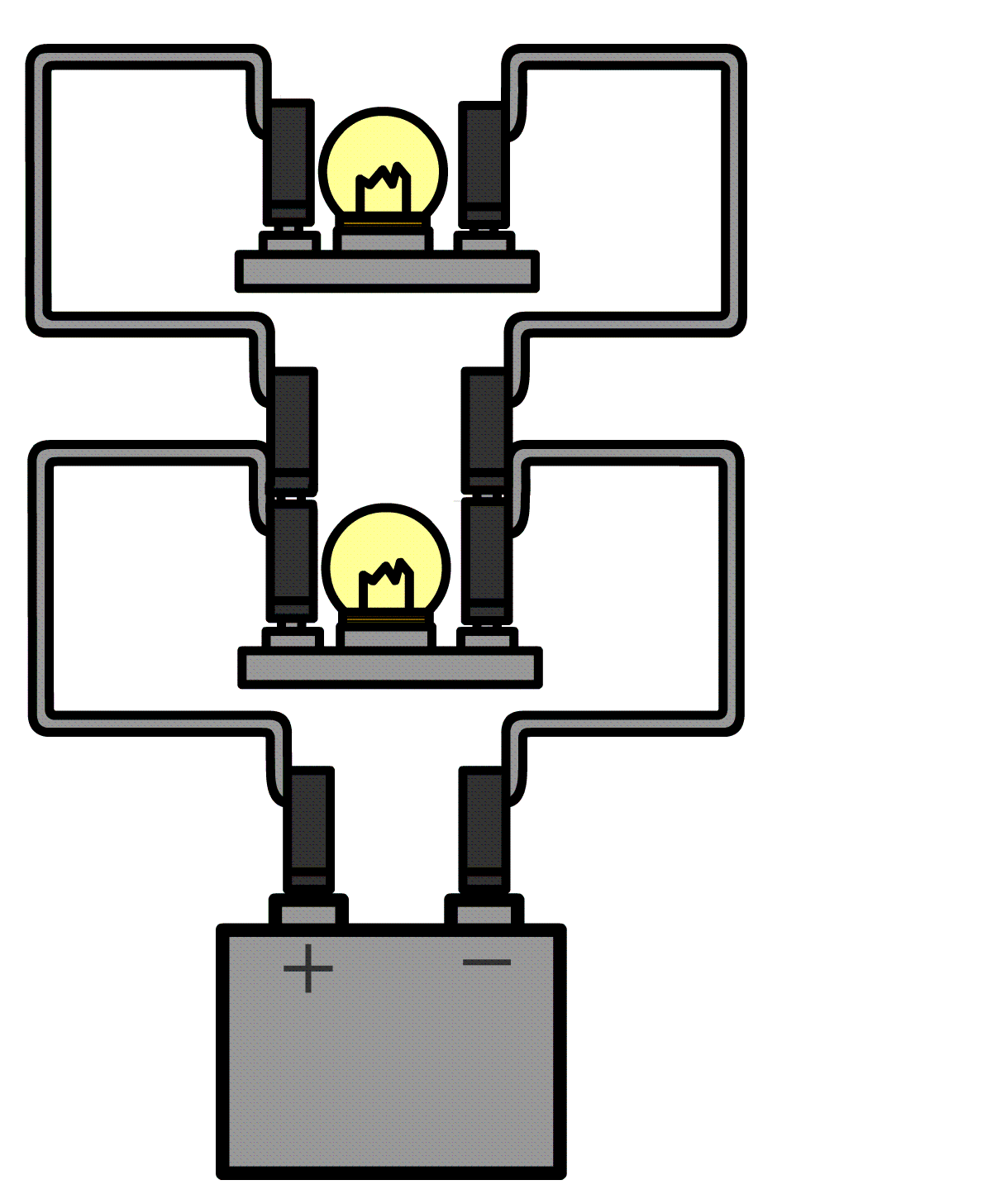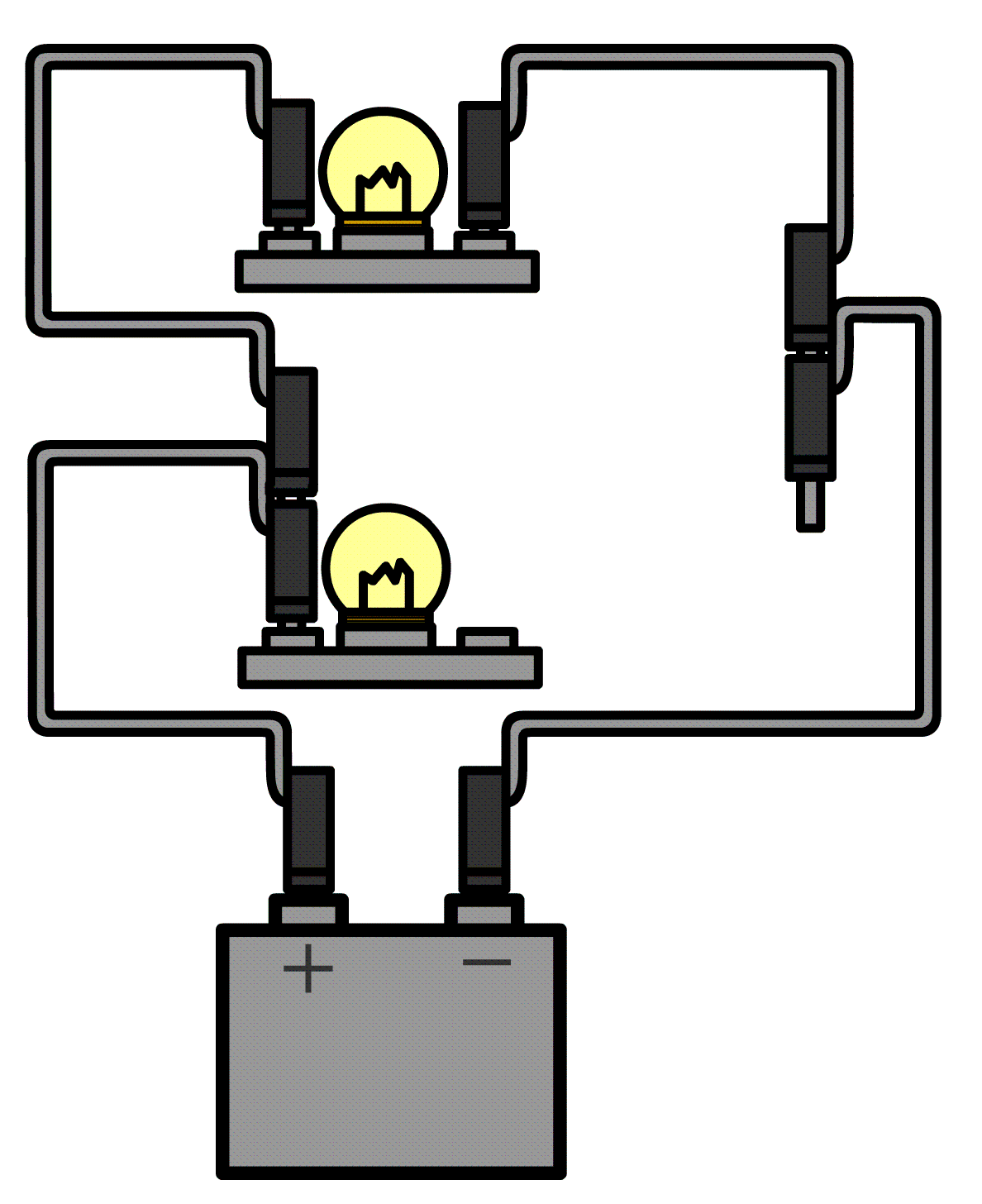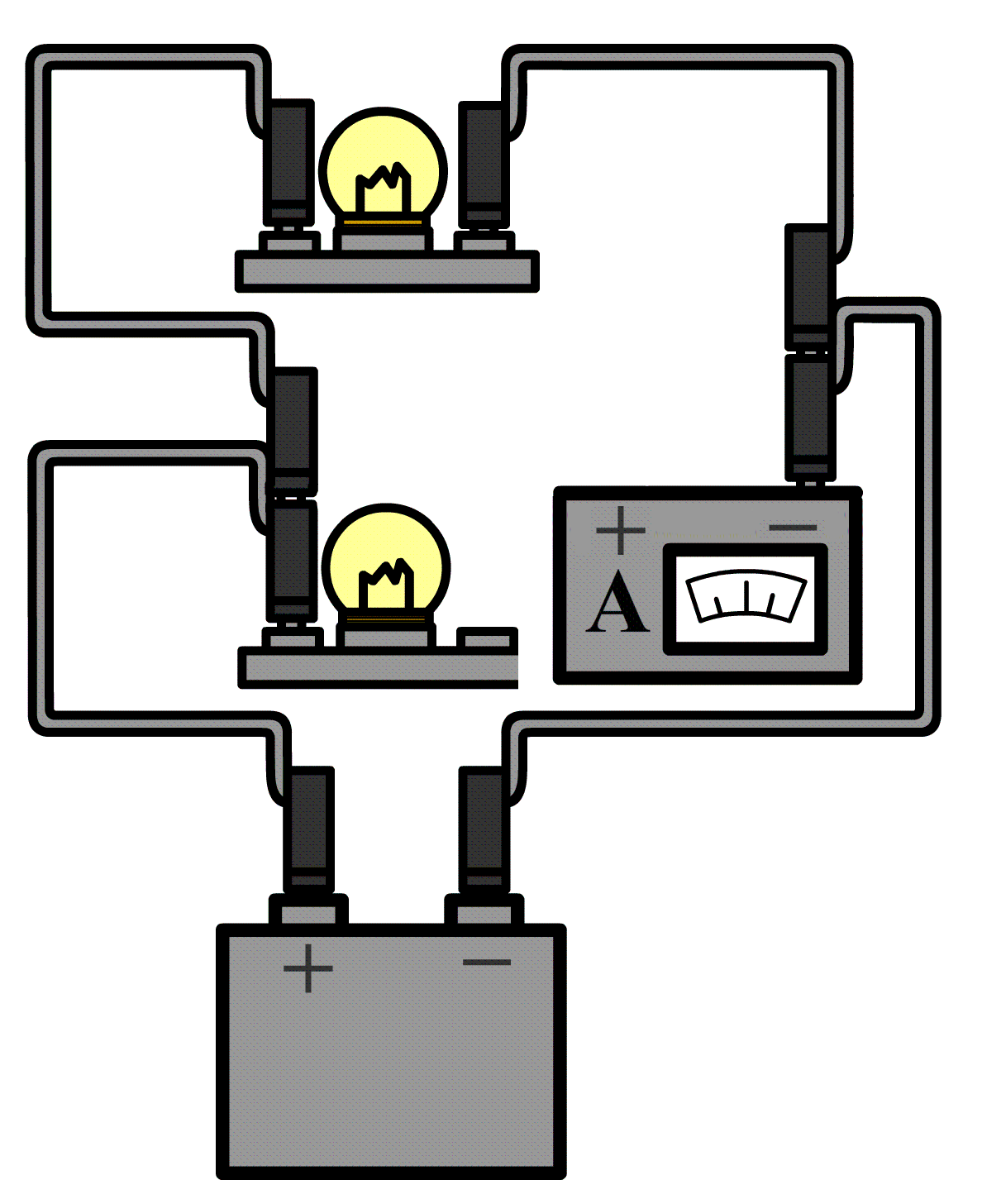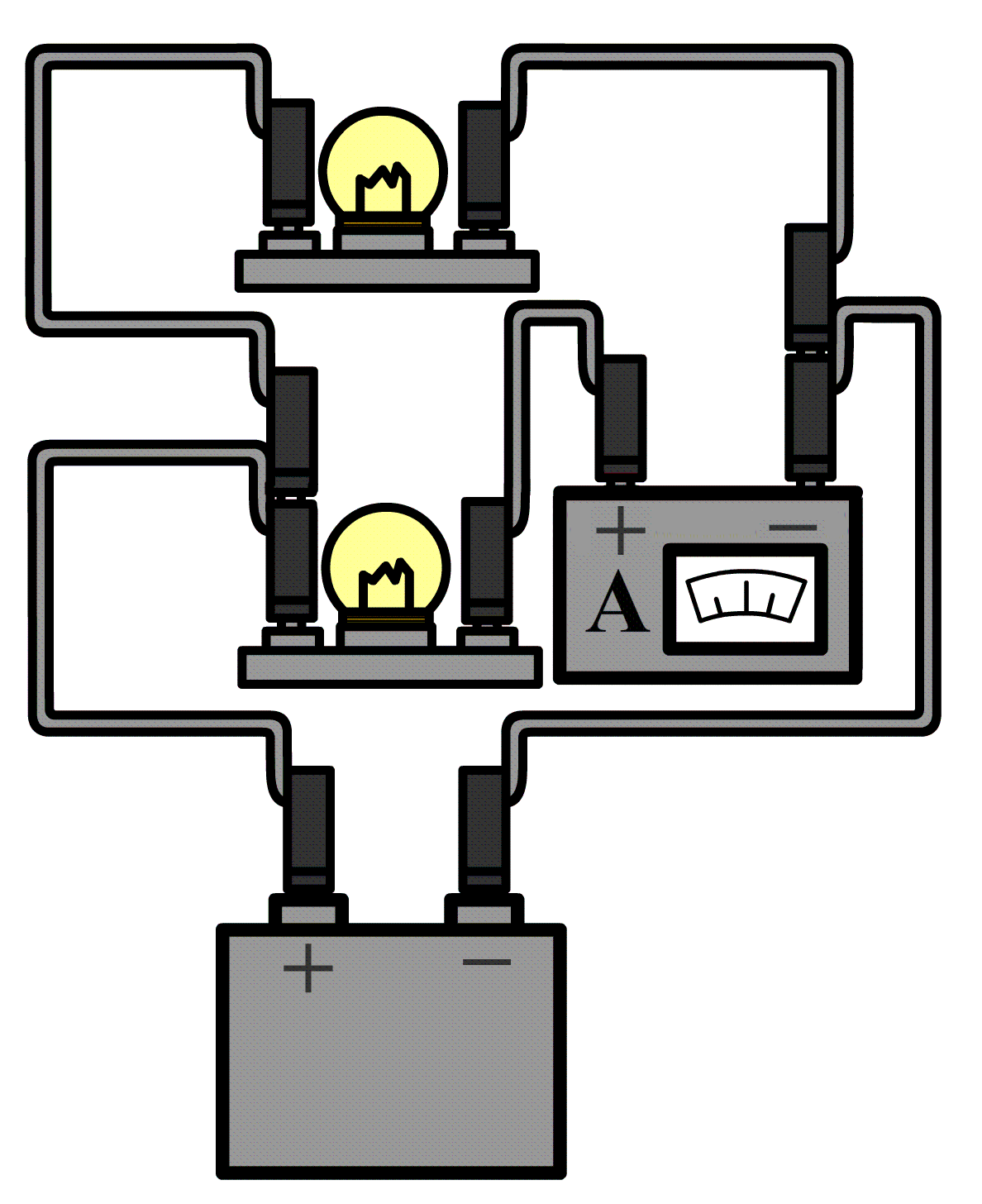
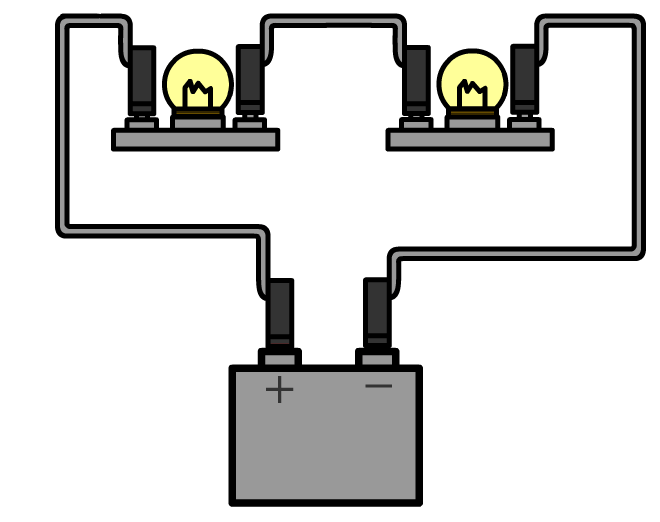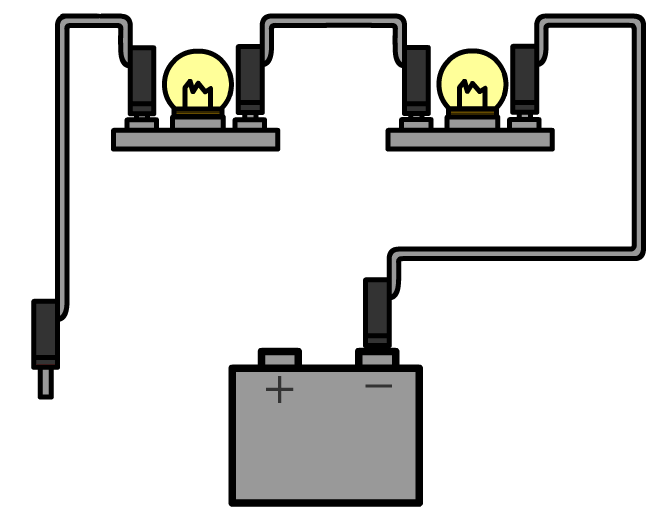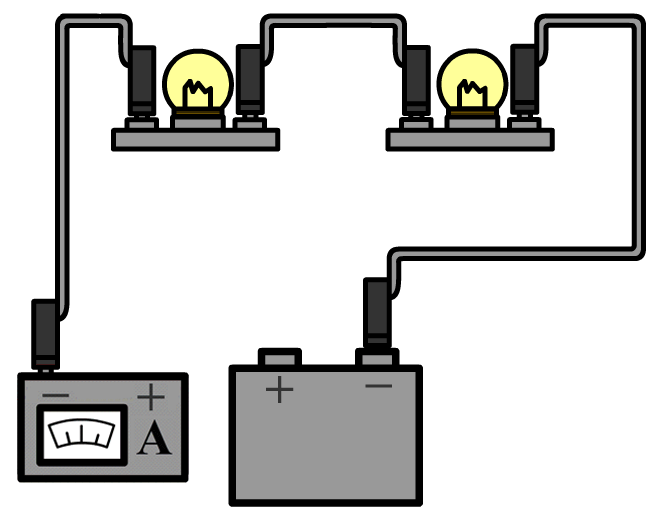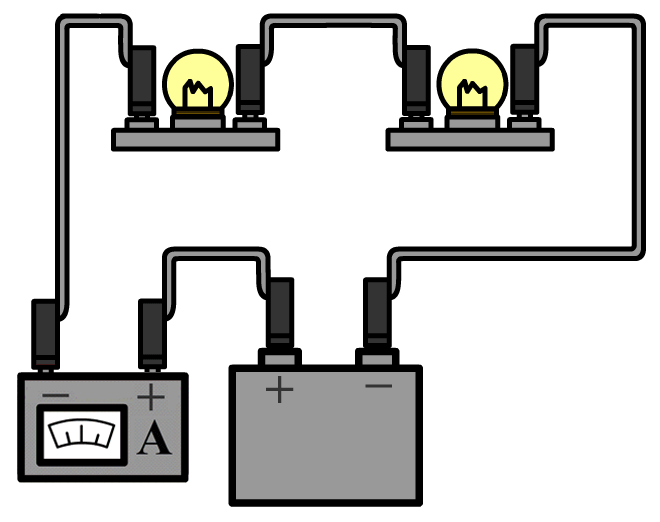
Ampèremeters zijn zo gemaakt dat ze de rest van de schakeling niet beïnvloeden. Voor de ampèremeter betekent dit dat ze een weerstand hebben van (zo goed als) 0 Ω. Op deze manier kan de stroom er ongestoord doorheen stromen.

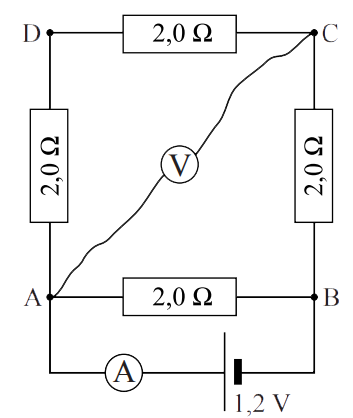
De spanning meten we met een zogenaamde voltmeter (ook wel spanningsmeter genoemd). De voltmeter sluit je parallel aan over het onderdeel waarvan je de spanning wilt meten. Dit doe je door de voltmeter aan beide kanten van een onderdeel aan te sluiten (zie de onderstaande afbeelding). Merk wederom op dat de pluspool van de spanningsbron verbonden is met de pluspoort van de voltmeter en de minpool met de minpoort.

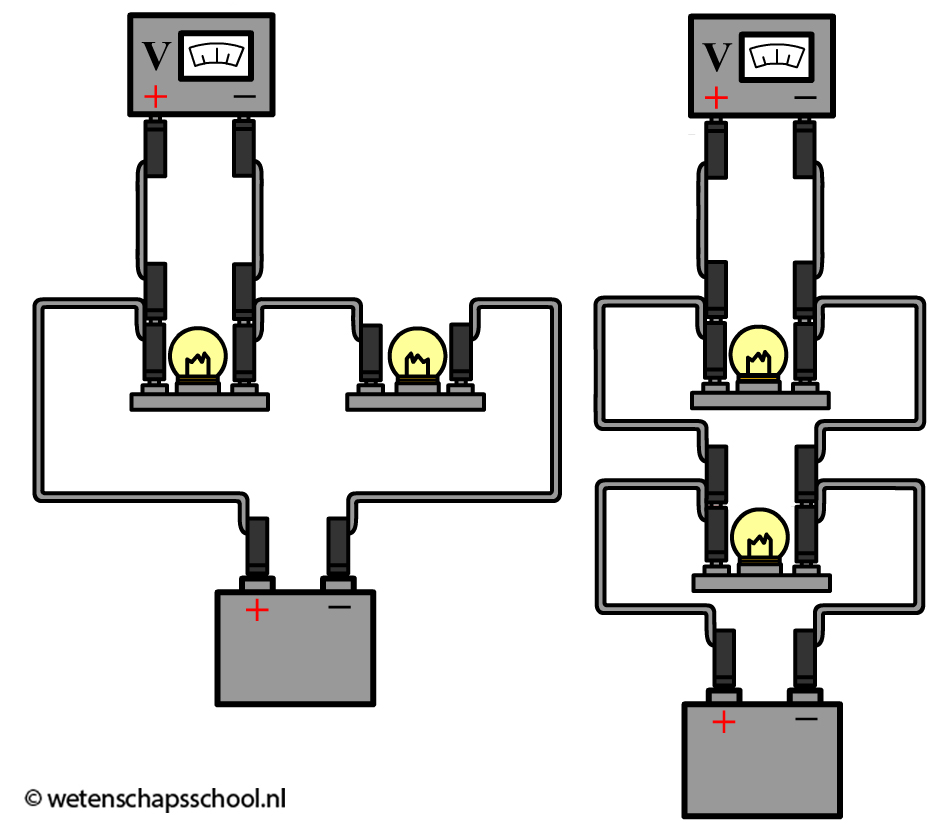
Ook de voltmeters zijn zo gemaakt dat ze de rest van de schakeling niet beïnvloeden. Voor voltmeters betekent dit dat ze een weerstand moeten hebben van (zo goed als) oneindig Ω. Op deze manier gaan de ladingen niet door de voltmeter heen en kunnen de ladingen ongestoord door het onderdeel stromen waarvan je de spanning wilt meten.

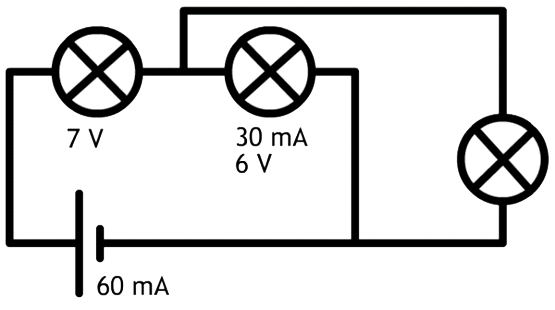
In sommige gevallen worden voltmeters niet direct over één onderdeel aangesloten. In dat geval is het van belang dat we iets beter snappen wat een voltmeter eigenlijk meet. In de volgende afbeelding zien we aangegeven hoeveel volt een lading op verschillende plekken over heeft. Let erop dat we hier weer 'doen alsof' de stroom van plus naar min stroomt.

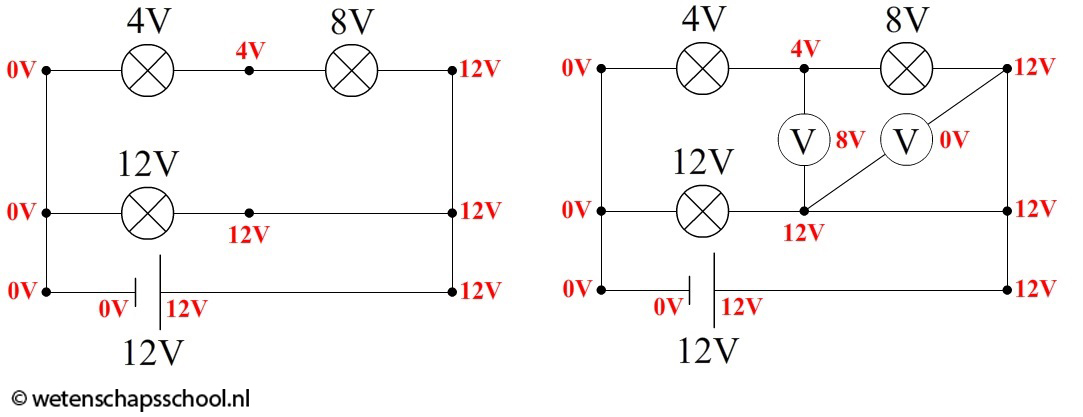
Als we een voltmeter op twee punten aansluiten, dan meet de voltmeter het spanningsverschil tussen deze twee punten. De linker voltmeter in de rechter afbeelding zit bijvoorbeeld tussen een spanning van 4V en een spanning van 12 V in. De voltmeter geeft daarom dus 12 - 4 = 8 V aan. Bij de rechter voltmeter is de spanning aan beide uiteinden 12 V. De voltmeter geeft hier dus 12 -12 = 0 V aan.

De stroom loopt altijd van hoge spanning naar lage spanning. In het linker voorbeeld gaat de stroom dus omhoog door de voltmeter. In het rechter voorbeeld is geen spanningsverschil. Hier loopt dus geen stroom doorheen.

       Correct aansluiten van stroom- en spanningsmeters

Een persoon wil metingen verrichten aan een parallelschakeling met twee lampen.

Teken de schakeling drie keer. In de eerste schakeling voeg je een ampèremeter toe om de stroomsterkte van het ene lampje te meten en in de tweede schakeling voeg je een ampèremeter toe om de stroomsterkte van het andere lampje te meten. In de derde schakeling laat je zien hoe je de stroomsterkte kan meten van de spanningsbron zelf.

(3p) Voer nogmaals opdracht a uit, maar nu door de onderstaande onderdelen op de correcte manier met elkaar te verbinden. De linker ingang van de ampèremeter is de plusingang en de rechter ingang de miningang.


Herhaal nu vraag a, maar dan met spanningsmeters.

(3p) Herhaal nu vraag b, maar dan met spanningsmeters.


       Aflezen van de voltmeter met behulp van het spanningsverschil

Een leerling maakt de onderstaande schakeling.

(1p) Leg uit dat de stroommeter in deze schakeling een weerstand van ongeveer 0 Ω moet hebben om de schakeling niet te beïnvloeden.

(5p) Bereken de stroomsterkte die de stroommeter aanwijst.

(1p) De leerling sluit nu ook een spanningsmeter aan tussen de punten A en C.
Leg uit welke weerstand de spanningsmeter moet hebben om de schakeling niet te beïnvloeden.

(2p) Bereken de spanning die de spanningsmeter aanwijst.
(bron: examen HAVO 2013-1)

Een leerling heeft een zonvolgsysteem gemaakt. Dit is een opstelling met een zonnepaneel dat meedraait met de zon, zodat het zonnepaneel steeds loodrecht op de invallende zonnestralen staat. Het zonvolgsysteem bevat onder andere twee exact dezelfde LDR's met daartussen een schotje. Als de zon niet recht boven de twee LDR's staat, valt er een schaduw van het schotje op één van de twee LDR's. Dit is in de onderstaande afbeelding schematisch weergegeven:
De leerling plaatst de twee LDR's in de volgende schakeling met een elektromotor die de opstelling kan laten draaien.

(3p) Leg uit dat de motor niet werkt als er evenveel licht op beide sensoren valt.

(4p) Na een tijdje is de zon een beetje gedraaid en valt er een schaduw over LDR₂. Hierdoor neemt de weerstand van de LDR toe. Leg uit of de stroom gaat lopen van punt B naar C of van punt C naar B.
(bron: examen VWO 2017-1)

§5 Vervangingsweerstand

In deze paragraaf gaan we leren de totale weerstand van een schakeling te bepalen. We doen dit met het concept vervangingsweerstand.

Eerder in dit hoofdstuk hebben we gelezen dat de spanningsbron zelf geen weerstand heeft. Toch kunnen we wel spreken van de totale weerstand van een schakeling. We gebruiken hiervoor het begrip vervangingsweerstand (R_v). In de onderstaande afbeelding zien we bijvoorbeeld links twee weerstanden in serie. Rechts zijn deze twee weerstanden vervangen door één vervangingsweerstand.

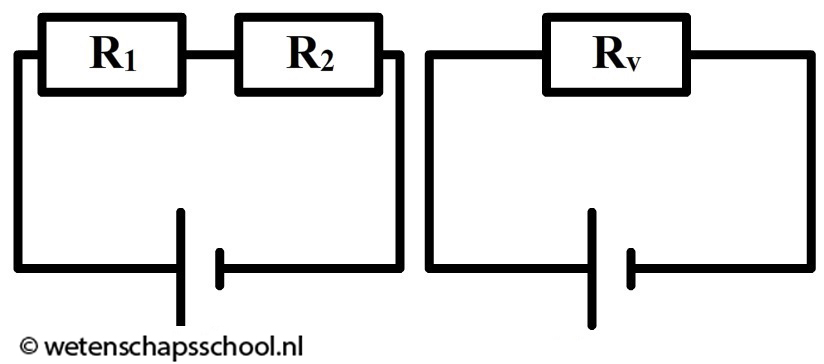
De vervangingsweerstand van twee weerstanden in serie is gelijk aan:

$$ R_v = R_1 + R_2 \;\;\;\;\;\;\;\;\;\; \mathrm{(serie)} $$

Vervangingsweerstand (R_v)

ohm (Ω)

Weerstand van onderdeel 1 (R₁)

ohm (Ω)

Weerstand van onderdeel 2 (R₂)

ohm (Ω)

Ook twee parallelle onderdelen kunnen we vervangen door een vervangingsweerstand:

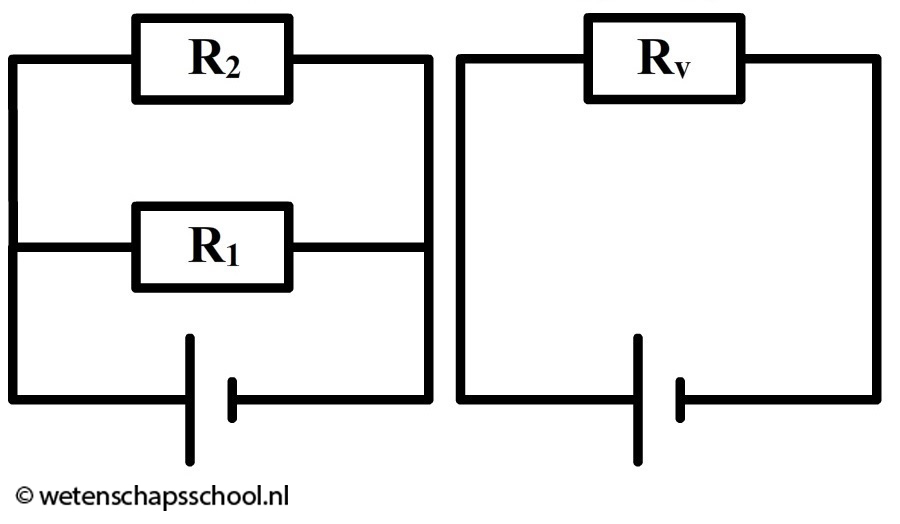
In dat geval geldt:

$$ \frac{1}{R_v} = \frac{1}{R_1} + \frac{1}{R_2} \;\;\;\;\;\;\;\;\;\; \mathrm{(parallel)} $$

Ook van gemengde schakelingen kunnen we de vervangingsweerstand uitrekenen, maar dan moeten we dit in meerdere stappen doen. Kijk bijvoorbeeld eens naar de linker onderstaande schakeling. Eerst vervangen we de twee weerstanden in serie door een vervangingsweerstand R_v,12 (zie de middelste afbeelding). Omdat deze weerstanden in serie staan, gebruiken we:

$$ R_{v,12} = R_1 + R_2 $$

We hebben de gemengde schakeling nu vereenvoudigd tot een gewone parallelschakeling. De totale vervangingsweerstand berekenen we dan als volgt:

$$ \frac{1}{R_v} = \frac{1}{R_3} + \frac{1}{R_{v,12}} $$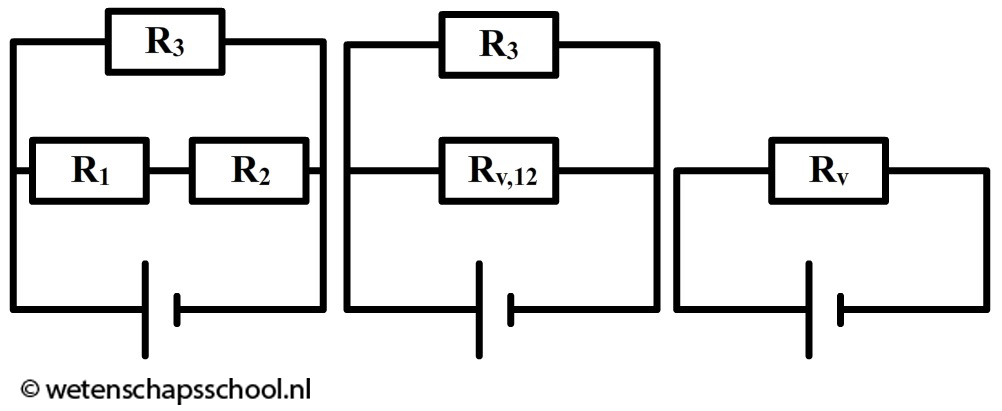

Voorbeeld

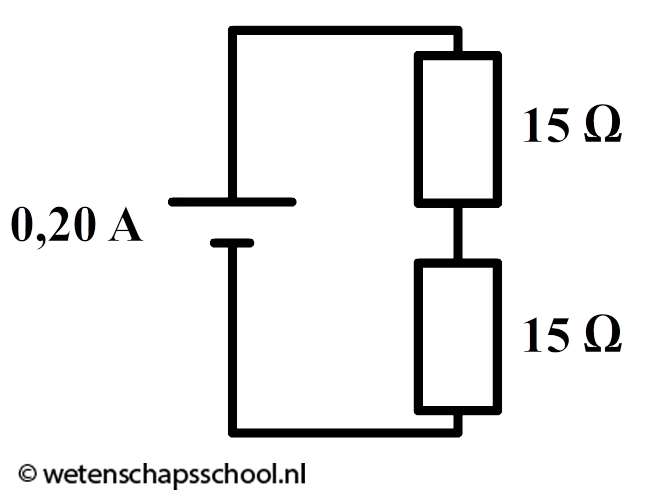
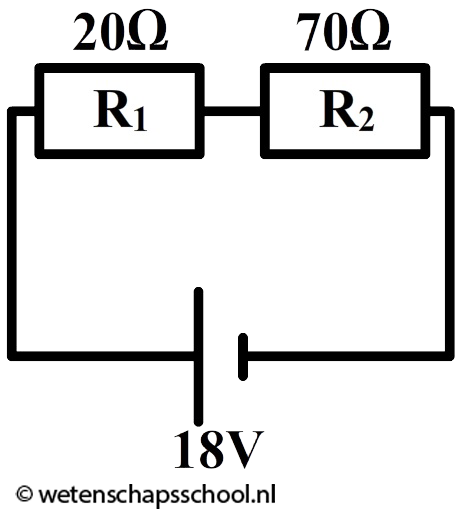
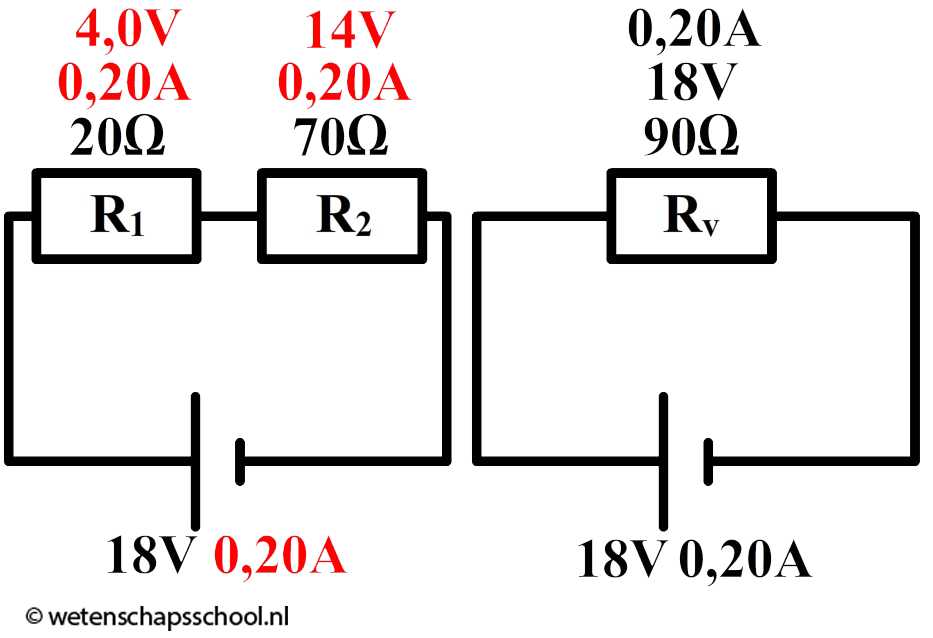
Vraag:

In een serieschakeling zijn twee weerstanden opgenomen. Eén van de weerstanden heeft een waarde van 20 Ω en de ander van 70 Ω. De spanning over de spanningsbron is 18 V. Bereken de spanning over de linker weerstand.

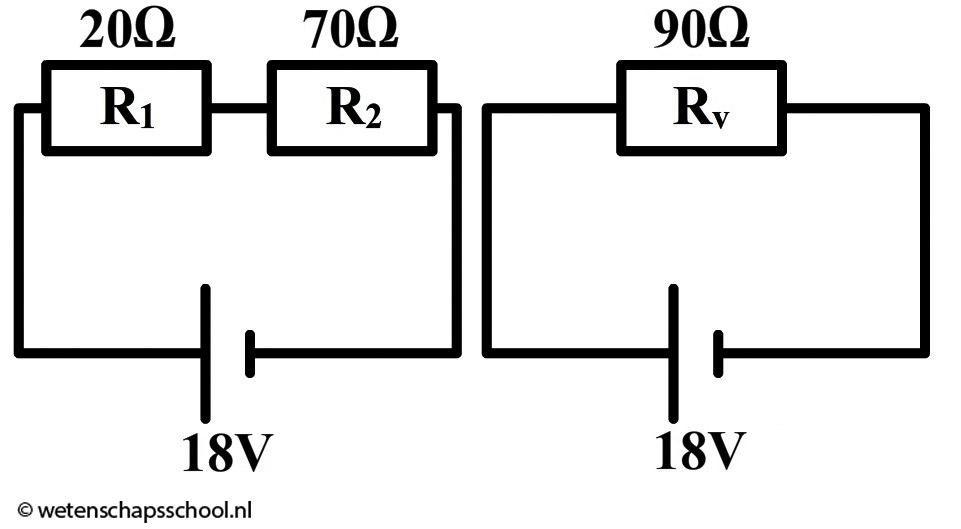
Antwoord:

Eerst berekenen we de vervangingsweerstand:
$$ R_v = R_1 + R_2 $$ $$ R_v = 20 + 70 = 90 \;\Omega $$

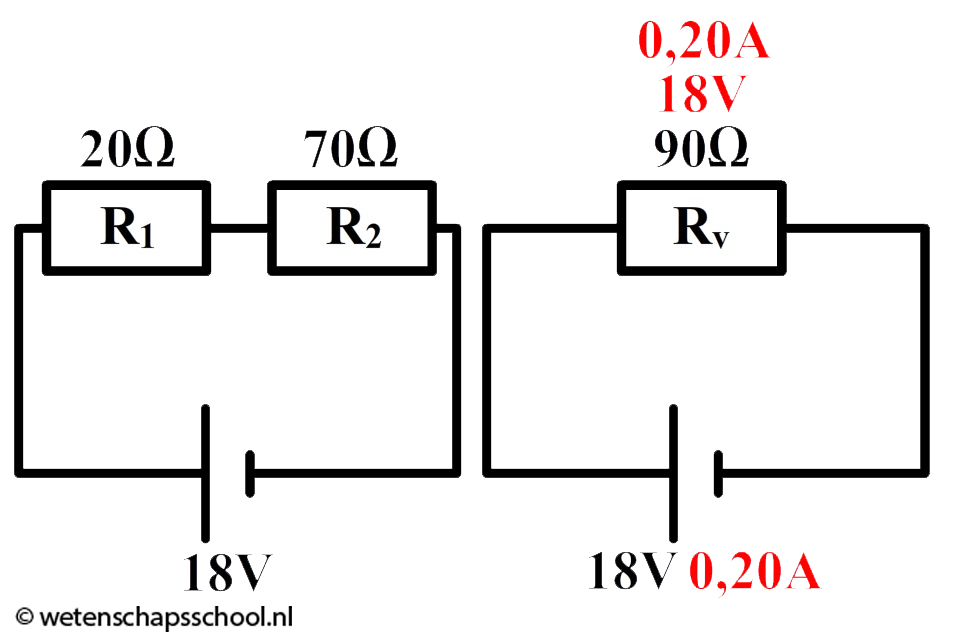
Met de vervangingsweerstand is de schakeling simpeler geworden (zie de onderstaande schakeling). Als gevolg kunnen we nu de stroomsterkte van de spanningsbron uitrekenen:
$$ I = \frac{U}{R} $$ $$ I = \frac{18}{90} = 0,20 \text{ A} $$

Met dit gegeven kunnen we verder gaan rekenen aan de oorspronkelijke schakeling. Omdat de stroomsterkte in een serieschakeling overal gelijk is, weten we dat de stroomsterkte door de linker weerstand ook 0,20 A is. De spanning over deze weerstand wordt dus:
$$ U_1 = IR_1 $$ $$ U_1 = 0,20 \times 20 = 4,0 \text{ V} $$

Omdat het vaak voorkomt dat we willen weten hoe de spanning zich verdeelt over twee weerstanden in serie, is het handig om het resultaat van het vorige voorbeeld sneller te kunnen vinden. De verhouding tussen de linker weerstand (20 Ω) en de vervangingsweerstand (90 Ω) blijkt gelijk aan de verhouding tussen de linker spanning en de spanning over de bron:

$$ \frac{U_1}{U_{bron} } = \frac{R_1}{R_v} $$

Dit kunnen we omschrijven naar:

$$ U_1 = \frac{R_1}{R_v}\times U_{bron} $$

In dit geval vinden we:

$$ U_1 = \frac{20}{90} \times 18 = 4 \text{ V} $$

Voorbeeld

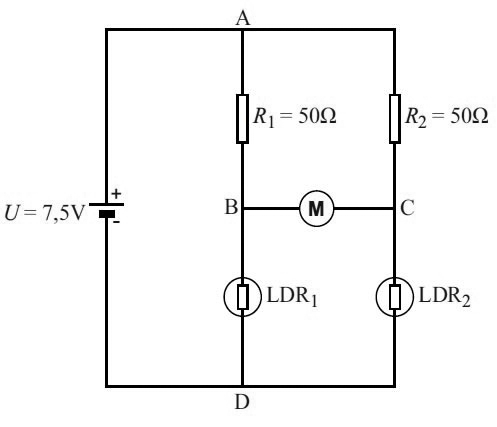
Vraag:

In een parallelschakeling zijn twee lampjes opgenomen. Eén van de lampjes heeft een weerstand van 20 Ω en het andere lampje heeft een weerstand van 50 Ω. Bereken de vervangingsweerstand van deze schakeling.

Antwoord:

We rekenen de vervangingsweerstand als volgt uit:
$$ \frac{1}{R_v} = \frac{1}{R_1} + \frac{1}{R_2} $$ $$ \frac{1}{R_v} = \frac{1}{20} + \frac{1}{50} $$ $$ \frac{1}{R_v} = 0,05 + 0,02 = 0,07 $$ $$ R_v = \frac{1}{0,07} = 14 \;\Omega $$
De vervangingsweerstand van de parallelschakeling is dus 14 Ω.

Zoals je kunt zien is de vervangingsweerstand kleiner dan de weerstanden van de componenten! Dit klinkt verrassend, maar is goed te begrijpen. Door twee parallelle weerstanden gaan namelijk meer elektronen dan door één afzonderlijke weerstand. De vervangingsweerstand laat dus meer ladingen door dan de afzonderlijke weerstanden en heeft dus een kleinere weerstand!

Voorbeeld

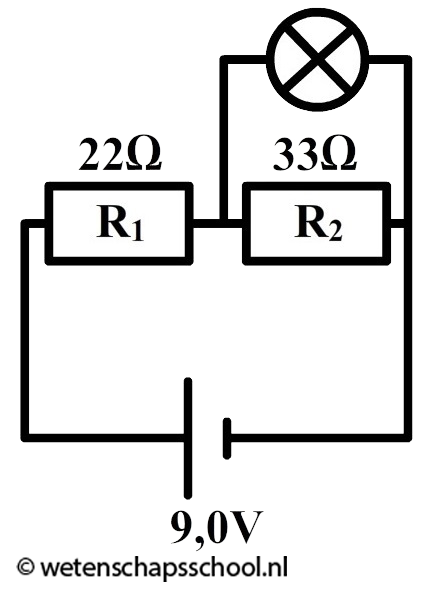
Vraag:

Twee weerstanden worden in serie aangesloten op een spanningsbron. Dan wordt parallel aan de rechter weerstand een extra lampje toegevoegd. Laat zien of dit ervoor zorgt dat de spanning over de rechter weerstand groter wordt, kleiner wordt of gelijk blijft.

Antwoord:

Als we het lampje parallel aansluiten, dan wordt de vervangingsweerstand van de gehele schakeling automatisch kleiner (zie het vorige voorbeeld). Als gevolg wordt de stroomsterkte die de spanningsbron levert groter.

Weerstand R₁ staat in serie met de spanningsbron. De stroomsterkte door de spanningsbron is dus gelijk aan de stroomsterkte door weerstand R₁. Met een vaste weerstand en een toenemende stroomsterkte vinden we met de formule U = IR dat de spanning over weerstand R₁ toeneemt.

De spanning over R₁ en R₂ tezamen moet gelijk zijn aan de spanning van de spanningsbron (U_bron = U₁+U₂). Omdat de spanning over R₁ stijgt en de spanning van de bron gelijk blijft, moet de spanning over weerstand R₂ dalen. De spanning over weerstand R₂ wordt dus kleiner op het moment dat we het extra lampje parallel aansluiten.

Rekenen met de vervangingsweerstand

Ga naar deze opdracht op de website of maak het stencil aan het eind van de paragraaf.

Maak de onderstaande opdracht:

Twee lampjes met een weerstand van 10 Ω worden eerst parallel en dan in serie aangesloten.

(3p) Bereken in beide gevallen de vervangingsweerstand.

(1p) De vervangingsweerstand in de parallelschakeling is kleiner dan de weerstanden van de lampjes. Verklaar hoe dit kan.

(6p) Een leerling maakt de volgende schakeling:
Bereken de stroomsterkte door elk onderdeel van de schakeling.

(3p) De leerling bouwt de schakeling zoals hieronder is weergegeven. In deze schakeling worden zes snoeren gebruikt met elk een weerstand van 0,023 Ω. De leerling wil dat de stroomsterkte door de stroommeter gelijk wordt aan 20 A. Bereken de spanning die dan over de voeding moet staan.

(bron: examen VWO 2013-2)

(5p) In de onderstaande afbeelding zien we een verlengsnoer dat om een haspel gewikkeld is. Het verlengsnoer omvat een aanvoerende en afvoerende draad. Deze worden de aders genoemd. Eerst wordt een lamp aangesloten op het verlengsnoer en daarna wordt ook een kachel parallel aangesloten op het verlengsnoer. De schakeling is hieronder weergegeven. Bij het aansluiten van de kachel blijkt de lamp iets minder fel te branden. Leg uit waarom.

(bron: examen HAVO 2007-1)

Een leerling wil zelf een temperatuursensor in elkaar zetten. Hij wil dat de sensor bij een hogere temperatuur een hogere spanning geeft. Hij bedenkt hiervoor de volgende drie schakelingen:
Uiteindelijk blijkt alleen schakeling C te doen wat de leerling wil. Hieronder zien we de grafiek van de sensorspanning tegen de temperatuur geschetst behorende bij deze schakeling.

(3p) Leg uit hoe het komt dat schakeling C bij een hogere temperatuur een hogere sensorspanning geeft.

(2p) Schets in het bovenstaande diagram de grafieken van de sensorspanning van schakeling A en schakeling B. Licht je keuzes toe. (bron: examen VWO 2010-1)

(VWO) Een leerling wil krachten meten in een aantal attracties in een attractiepark. Hij maakt daarvoor zelf een eenvoudige krachtsensor. De elektrische schakeling van de krachtsensor staat hieronder weergegeven. Op de druksensor ligt een knikker die bij beweging in een attractie met een bepaalde kracht tegen de drukweerstand drukt. De batterij levert een spanning van 9,0 V.
Hieronder zien we in het linker diagram hoe de waarde van de drukweerstand afhangt van de kracht die de knikker uitoefent. In het rechter diagram zien we het verband tussen de uitgangsspanning van de sensor en de kracht.

(3p) Laat met een beredenering zien dat de sensorspanning in het rechter diagram overeenkomt met de spanning over aansluitpunten B en C (en niet A en B).

(5p) Bepaal de waarde van de weerstand R in de schakeling.
(bron: examen VWO 2014-1)

(VWO) In de onderstaande afbeelding zien we een zogenaamde spanningsdeler. Dit is een schakeling waarbij we de spanning van de spanningsbron kunnen omzetten naar een lagere spanning. We gebruiken hiervoor een variabele weerstand.

(2p) Beredeneer dat hoe groter deel R₁ van de variabele weerstand is, hoe groter de spanning over aansluitingen A en B moet zijn.

(3p) De spanning over aansluitingen A en B wordt gegeven door: $$ U_{AB} = \frac{U_{bron}}{R_v} R_1 $$ Leid deze formule af met behulp van formules uit BINAS.

(VWO, 2p) Op een elektrische gitaar zijn zogenaamde elementen gemonteerd die de mechanische trillingen van de snaren omzetten in elektrische trillingen. De spanning die over deze elementen ontstaat noemen we de uitgangspanning. Deze uitgangsspanning wordt met behulp van twee draden over een variabele weerstand gezet (zie de onderstaande schakeling). Aan deze weerstand zit een knop waarmee het volume van de elektrische gitaar geregeld kan worden. Dit werkt als volgt. Door aan de knop te draaien kan de gitarist de grootte van de spanning regelen die naar de versterker (en dus naar de luidspreker) gaat. Leg uit in welke richting, linksom (L) of rechtsom (R), de knop gedraaid moet worden om het volume van de gitaar zachter te zetten.

(bron: examen VWO 2019-2)

STENCIL VERVANGING

§6 Soortelijke weerstand

In deze paragraaf gaan we de weerstand van een draad bepalen.

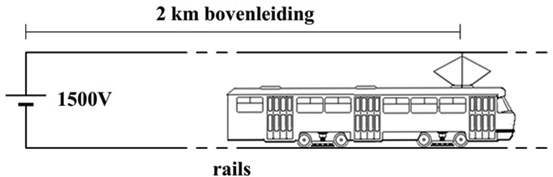
Tot nu toe hebben we alleen gekeken naar de weerstand van lampjes, maar niet van de bedrading zelf. Dit komt omdat de weerstand van een korte draad verwaarloosbaar is ten opzichte van de weerstand van bijvoorbeeld een lampje. Als draden echter heel lang worden, dan gaat de weerstand wel een rol spelen. Denk bijvoorbeeld aan hoogspanningskabels (zie de onderstaande afbeelding).

We kunnen de weerstand van een draad uitrekenen met deze formule:

$$ R = \frac{\rho\;l}{A} $$

Weerstand (R)

ohm (Ω)

Soortelijke weerstand (ρ)

ohm-meter (Ωm)

Lengte (l)

meter (m)

Doorsnede (A)

vierkante meter (m²)

De soortelijke weerstand (ρ) is een materiaaleigenschap die we voor verschillende stoffen in BINAS kunnen vinden (niet te verwarren met de dichtheid, waar we hetzelfde teken voor gebruiken!). In beide gevallen wordt immers van het symbool ρ gebruik gemaakt. De doorsnede (A) van de draad is het oppervlak dat je vindt als je de draad zou doorsnijden (zie de rechter onderstaande afbeelding). Met behulp van de doorsnede kan de straal (r) en de diameter (d) van de draad berekend worden met deze formules:

$$ A = \pi r^2 $$ $$ d = 2r $$

Rekenen met de formule voor de soortelijke weerstand

(5p) Een metaaldraad met een lengte van 80 cm en een diameter van 2,19 mm heeft een weerstand van 9,1 mΩ. Laat met een berekening zien van welk metaal deze draad gemaakt is.

(4p) Een constantaandraad heeft een lengte van 5,0 m en een diameter van 0,20 mm. Bereken de weerstand van de draad.

(7p) Een elektrische boiler is aangesloten op de netspanning. Het verwarmingselement van de boiler is gemaakt van nichroomdraad met een lengte van 45 m en een diameter van 0,89 mm. Bereken hoeveel kWh aan elektrische energie er in de boiler verbruikt wordt als deze 5,0 uur aan staat.

(4p) Een gloeidraad van een gloeilamp is gemaakt van wolfraam. De weerstand bij kamertemperatuur van deze draad is 70 Ω. De lengte van de draad is 45 cm. Bereken de diameter van de draad in micrometer.

(5p) In een tl-buis loopt een stroom door een gas. De inwendige diameter van de buis is 8,5 mm en de lengte is 40 cm. Het vermogen van de buis is 9,0 W en de buis is aangesloten op de netspanning. Bereken de soortelijke weerstand van het gas.

Redeneren met de formule voor de soortelijke weerstand

(1p) Beredeneer wat er gebeurt met de weerstand van een draad als de draad 2,0× zo lang wordt.

(2p) Beredeneer wat er gebeurt met de weerstand van een draad als de draad 2,0× zo dik wordt.

(1p) Beredeneer wat er gebeurt met de soortelijke weerstand van een draad als de draad 2,0× zo dik wordt.

(VWO) Om te controleren of een brug niet te zwaar belast wordt, maakt men gebruik van sensoren. In zo'n sensor zit een zogenoemd rekstrookje, dat op een kabel van de brug is geplakt. In zo'n rekstrookje is een lange, dunne constantaandraad verwerkt. Deze draad heeft een weerstand van 350 Ω.

(3p) Als er veel verkeer op de brug is, rekt de kabel een beetje uit en hierdoor verandert de weerstand van het rekstrookje. Door deze weerstandsverandering te meten, weet men of de kabel te veel uitrekt. Als het strookje uitrekt, wordt de weerstand van de constantaandraad groter. Geef twee redenen hiervoor.

(5p) De weerstandsverandering van het rekstrookje kan bepaald worden met de volgende schakeling:

Als de weerstand van het rekstrookje 1,0 Ω groter wordt, verandert de spanning die de spanningsmeter aangeeft minder dan een half procent. Toon dat aan.

(3p) Dit is een erg kleine verandering. Om de weerstandsverandering beter te meten, wordt de volgende schakeling gebruikt:
Als het rekstrookje niet is uitgerekt, geeft de spanningsmeter 0,000 V aan. Leg dit uit.

(2p) Bereken welke spanning de voltmeter in deze schakeling aangeeft als we de weerstand van het rekstokje met 1,0 Ω vergroten.
(bron: examen VWO 2012-2)

De spanning van een batterij van 1,5 V zakt langzaam naarmate de batterij verder leeg raakt. Op sommige batterijen zit daarom een tester om te zien hoe 'vol' de batterij nog is. De tester bestaat uit geleidende strip metaal met temperatuurgevoelige verf. Als je met twee vingers op de tester drukt, maakt hij contact met de beide polen van de batterij. Doordat er dan een stroom door de tester loopt, wordt deze warm. Hierdoor verkleurt de temperatuurgevoelige verf. In de onderstaande afbeelding is de strip schematisch weergegeven. We kunnen ons de strip voorstellen als vijf strookjes metaal die overal even dik zijn maar sprongsgewijs breder worden.

Het dunste deel is 1,0 mm breed en heeft een weerstand van 1,3 Ω. De volgende strookjes zijn achtereenvolgens 2,0 mm, 3,0 mm, 4,0 mm en 5,0 mm breed.

(4p) Bereken de weerstand van de gehele strip.

(3p) Als de batterij niet helemaal vol is, kleurt de strip aan de ene kant lichter dan aan de andere kant. Aan de ene kant van de strip is de temperatuur kennelijk hoger dan aan de andere. Leg uit of de temperatuur aan de smalle of aan de brede kant van de strip het hoogst wordt.

(4p) De fabrikant wil het ontwerp van de tester aanpassen, zodat deze geschikt wordt voor een batterij van 9,0 V. De fabrikant wil dezelfde temperatuurgevoelige verf blijven gebruiken, maar kan wel de strip aanpassen. Noem twee manieren waarop dit gedaan kan worden.
(bron: examen VWO 2011-1)

BINAS:
16	Electrotechnische symbolen
8-12	Soortelijke weerstand
7	Elektronlading
5	Kilowattuur

Hoofdstuk 7 Elektriciteit

§1 Lading

§2 Stroomsterkte en spanning

§3 De Wet van Ohm

§4 Stroom- en spanningsmeters

§5 Vervangingsweerstand

§6 Soortelijke weerstand

Hoofdstuk 7
Elektriciteit