Hoofdstuk 6
Modelleren (VWO)
§1 Modelleren
In dit hoofdstuk gaan we de computer gebruiken voor het beschrijven van natuurkundige processen. We doen dit met behulp van natuurkundige modellen. In deze paragraaf introduceren we een programma waarmee dergelijke modellen te maken zijn.
In dit hoofdstuk gaan we leren modelleren. Laten we met een simpel voorbeeld van een model beginnen. Stel een leerling heeft op een bepaald tijdstip 15 euro in zijn spaarpot en krijgt elke week 2 euro zakgeld. Met een model kunnen we dan een grafiek maken waarbij we de hoeveelheid geld in zijn spaarpot uitzetten tegen de tijd. Klik op 'play' om het resultaat te zien:
Links van de grafiek zien we twee kolommen. In de rechter kolom vullen we de zogenaamde startwaarden in. Hier vullen we voor alle relevante grootheden de beginwaarde in. Ook noteren we hier constanten die we nodig hebben. Met de eerste regel zorgen we dat we de tijd starten op tijdstip t = 0. Met de tweede regel bepalen hoe groot een tijdstapje dt is. Met de laatste twee regels bepalen we hoeveel geld er aan het begin in de spaarpot zit en hoeveel zakgeld elke week gegeven wordt.
In de linker kolom noteren we de zogenaamde modelregels. Hier schrijven we een aantal wiskundige operaties op, waarmee het programma kan uitrekenen wat de waarde van de relevante grootheden gaat zijn een tijdstapje dt later. Elk tijdstapje worden al deze regels dus doorlopen. We noemen dit herhaaldelijk doorlopen van de regels een iteratief proces.
Bij dit model lezen we:
- t = t + dt
- spaarpot = spaarpot + zakgeld
In de eerste regel wordt de tijd t een tijdstapje dt vooruitgezet. Het '='-teken dat we in deze modelregels zien heeft niet de gebruikelijke betekenis. Bij modelleren staat het '='-teken voor het woord 'wordt'. In woorden is de eerste modelregel dus:
- De nieuwe tijd t wordt gelijk aan de huidige tijd t plus een tijdstapje dt
De tweede modelregel vertelt ons dat de nieuwe waarde in de spaarpot gelijk wordt aan de huidige waarde plus het zakgeld.
Nog een voorbeeld. Een leerling heeft 50 euro en koopt hiervan elke dag een broodje van 3,40 euro. Als hij echter minder dan 20 euro over heeft, dan gaat hij iets zuiniger aan doen en koopt hij een broodje van slechts 1,40 euro. Als zijn geld op is, dan kan hij natuurlijk niks meer uitgeven. Op dit moment willen we dan ook dat de grafiek stopt. Het model ziet er dan als volgt uit:
Bij de modelregels wordt nu gebruik gemaakt van de als-dan-anders-stelling:
- als(spaarpot > 20)
- dan{kosten = 3.4}
- anders{kosten = 1.4}
Hier staat dat als er meer dan 20 euro in de spaarpot zit, dat de gemaakte kosten per dag dan 3,4 euro zijn. Als er minder dan 20 euro in de spaarpot zit, dan worden de kosten 1,4 euro. In de regel die hierop volgt wordt uitgerekend hoeveel geld de persoon na deze tijdstap nog overhoudt:
- spaarpot = spaarpot - kosten
Merk op dat de volgorde hier belangrijk is! Eerst moeten de kosten per dag bepaald worden en pas dan kan je uitrekenen hoeveel geld de persoon aan het eind van die dag overhoudt.
Uiteindelijk geven we het stop-commando als het geld op is:
- als(spaarpot < 0)
- dan{stop}
Let op dat we hier gebruik maken van een '<'-teken en niet van het '='-teken. Dit doen we omdat we werken in tijdstapjes dt en de kans klein is dat na een van deze tijdstapjes de persoon precies nul euro over zal hebben. Als gevolg zou bij gebruik van het '='-teken de grafiek gewoon doorlopen onder de horizontale as. Het '<'-teken zorgt ervoor dat het proces stopt zodra er een negatieve waarde bereikt wordt.
Hieronder vind je een lijstje met wiskundige symbolen die je bij het modelleren kan gebruiken:
|
Vermenigvuldigen |
* |
|
Delen |
/ |
|
Macht |
^ |
|
Wortel |
sqrt |
 Beheersen van de basisoperaties van modelleren
Beheersen van de basisoperaties van modelleren
|
|
§2 De vrije val
In deze paragraaf bestuderen we een model waarmee we een vrije val kunnen beschrijven.
Hieronder zien we het model van een steen die we met een snelheid van 40 m/s omhoogschieten vanaf hoogte x = 0. We verwaarlozen de wrijvingskrachten en spreken daarom van een vrije val:
Laten we eerst naar de startwaarden kijken:
- t = 0
- dt = 0.05
- x = 0
- v = 40
- g = -9.81
De hoogte x zetten we aan het begin op 0. De snelheid zetten we aan het begin op 40. De versnelling van een voorwerp dat een vrije val ondergaat is gelijk aan de valversnelling g = -9,81 m/s2. Het minteken geeft hier aan dat de versnelling naar beneden gericht is.
Nu de modelregels. De eerste drie regels zijn:
- t = t + dt
- v = v + g*dt
- x = x + v*dt
Met de tweede regel wordt elk tijdstapje de nieuwe snelheid van de steen berekend. Hoe komen we aan deze formule? Voor een vrije val geldt:
$$ g = \frac{\Delta v}{\Delta t} $$Dit kunnen we herschrijven tot:
$$ \Delta v = g \times \Delta t $$Δv staat voor de toename van de snelheid tijdens het tijdstapje Δt. Om de nieuwe snelheid uit te rekenen hebben we daarom de volgende regel nodig:
- v = v + dv
In woorden staat hier:
- De nieuwe snelheid v wordt gelijk aan de huidige snelheid v plus de toename van de snelheid dv .
Omdat dv = g*dt, wordt de regel:
- v = v + g*dt
Bij de modelregel x = x + v*dt gebeurt iets soortgelijks. Hier maken we gebruik van:
$$ v = \frac{\Delta x}{\Delta t} $$Dit schrijven we om tot:
$$ \Delta x = v \times \Delta t $$Δx staat voor de verplaatsing van de steen tijdens het tijdstapje Δt. Om de nieuwe hoogte uit te rekenen hebben we daarom de volgende regel nodig:
- x = x + dx
In woorden staat hier:
- De nieuwe hoogte x wordt gelijk aan de huidige hoogte x plus de toename van de hoogte dx .
Omdat dx = v*dt, wordt de regel:
- x = x + v*dt
In dit model hebben we ook nog een als-dan-stelling toegevoegd:
- als(x < 0)
- dan{stop}
Deze stelling zorgt ervoor dat de grafiek stopt als de steen de grond raakt. Het voorwerp raakt de grond als x = 0, maar we hebben hier toch gekozen voor de modelregel x < 0. Dit komt omdat het programma rekent in tijdstapjes van grootte dt en het dus mogelijk is dat de grafiek de tijd-as passeert zonder dat x ooit precies nul wordt.
 Modelleren van de vrije val
Modelleren van de vrije val
|
|
§3 De val met wrijving
In deze paragraaf voegen we de luchtwrijvingskracht toe aan het model.
In deze paragraaf voegen we wrijvingskracht toe aan ons model van een vallend voorwerp. In het onderstaande model laten we een steen vallen vanuit stilstand van een hoogte van 100 m. De steen heeft een massa van 1 kg, een frontaal oppervlak van 0,5 m2 en een wrijvingscoëfficiënt van 0,1. De dichtheid van de lucht maken we 1 kg/m3. Merk op dat de snelheid in de grafiek eerst toeneemt, maar uiteindelijk constant wordt. Dit is natuurlijk precies wat we verwachten bij een val met luchtwrijvingskracht.
Laten we de modelregels stap voor stap doornemen. In de tweede en de derde regel wordt de zwaartekracht en de wrijvingskracht gedefinieerd. Deze formules kunnen we vinden in het hoofdstuk 'kracht'. Bij modelleren maken we krachten die naar boven of naar rechts werken positief en krachten die naar beneden of naar links werken negatief. Omdat de zwaartekracht naar beneden werkt, moet deze dus negatief zijn. Hier wordt al automatisch aan voldaan, omdat we de valversnelling g negatief hebben gemaakt. De wrijvingskracht werkt in dit geval omhoog en moet dus positief zijn.
Met de individuele krachten kunnen we dan de resulterende kracht vinden. Omdat we al rekening gehouden hebben met de richting van de krachten, kunnen we hier de individuele krachten gewoon bij elkaar optellen:
- Fres = Fw + Fz
Nu we de resulterende kracht hebben kunnen we de tweede wet van Newton gebruiken om de versnelling van de steen te berekenen:
- a = Fres/m
Met de versnelling kunnen we dan de nieuwe snelheid vinden en met de nieuwe snelheid kunnen we de nieuwe hoogte vinden op de gebruikelijke manier (zie de vorige paragraaf):
- v = v + a*dt
- x = x + v*dt
Bij het maken van dit model hebben we de volgende stappen doorlopen:
- Bereken de individuele krachten
- Bereken de resulterende kracht
- Bereken de versnelling
- Bereken de nieuwe snelheid
- Bereken de nieuwe positie
De volgorde van deze stappen is van groot belang. De individuele krachten kunnen we direct uitrekenen met behulp van de startwaarden. Pas nadat we deze krachten hebben gedefinieerd, kunnen we de resulterende kracht berekenen. Pas daarna kunnen we met de tweede wet de versnelling berekenen etc.
Hieronder is het model uitgebreid om ook het omhooggooien van een voorwerp te kunnen beschrijven. Hier is het resultaat:
We hebben hier de volgende modelregels toegevoegd:
- als(v > 0)
- dan{Fw = -Fw}
Om deze regels te begrijpen moeten we nadenken over de richting van de wrijvingskracht tijdens de beweging. De luchtwrijvingskracht wijst altijd tegen de bewegingsrichting in. Als het voorwerp omhoog gaat, dan is de snelheid dus positief en als gevolg is de wrijvingskracht negatief (naar beneden). Als het voorwerp omlaag gaat, dan is de snelheid negatief en als gevolg is de wrijvingskracht positief (omhoog). Dit is precies wat we in de bovenstaande modelregels hebben gedaan. Als de snelheid positief is, dan wordt de wrijvingskracht negatief.
 Modelleren van een valbeweging met luchtwrijvingskracht
Modelleren van een valbeweging met luchtwrijvingskracht
|
|
§4 De worp
In deze paragraaf gaan we een model maken van een voorwerp dat we onder een hoek wegschieten.
In het onderstaande model wordt een worp van een steen beschreven. Voor het gemak is de wrijvingskracht verwaarloosd. Bij de startwaarden kan je zien dat de steen met een snelheid v van 8 m/s is weggeschoten onder een hoek h van 45 graden.
Bij de startwaarden hebben we de beginsnelheid opgedeeld in een horizontale component (vx) en een verticale component (vy). Deze componenten zijn in de rechter afbeelding te zien en ze zijn te berekenen met de sinus en de cosinus:
- vx = v*cos(h)
- vy = v*sin(h)
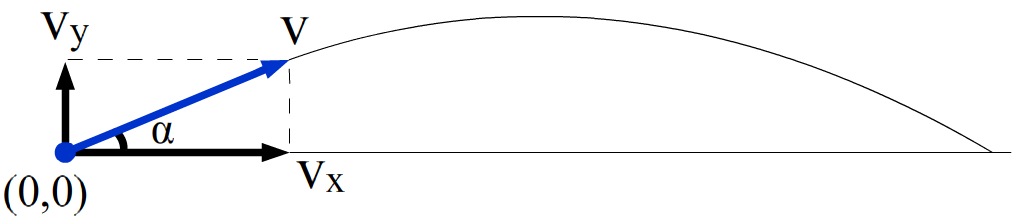
De zwaartekracht werkt alleen in de y-richting. De snelheid in de x-richting zal dus tijdens de beweging niet veranderen. We hebben dus alleen een modelregel nodig om vy elk tijdstapje aan te passen. Dit doen we op de gebruikelijke manier (zie paragraaf 2):
- vy = vy + g*dt
De positie verandert natuurlijk wel in zowel de x- als de y-richting:
- x = x + vx*dt
- y = y + vy*dt
 Modelleren met de worp
Modelleren met de worp
|
|
§5 De gravitatiekracht modelleren
In deze paragraaf gaan we een model maken van objecten in een baan om een hemellichaam.
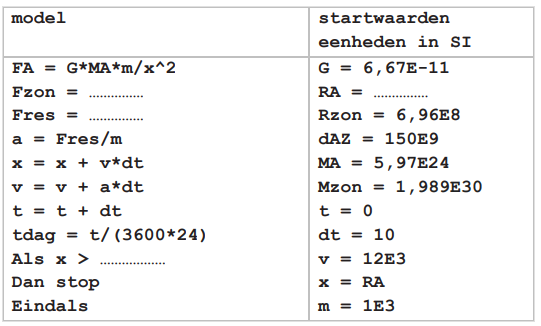
Het onderstaande model beschrijft de beweging van een planeet om een ster. We gebruiken hiervoor een x,y-diagram, waarbij we de ster op positie (0,0) plaatsen. De beginpositie van de planeet noemen we (x,y). De afstand van de ster tot de planeet noemen we 'r'. We kunnen r berekenen met de stelling van Pythagoras:
$$ r = \sqrt{x^2 + y^2} $$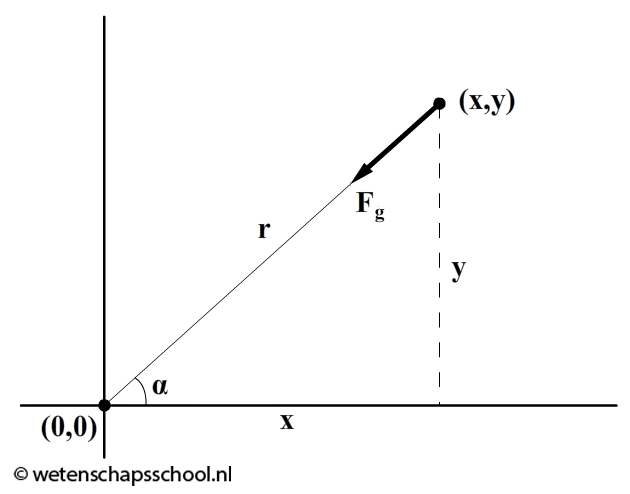
De formule voor de gravitatiekracht is geïntroduceerd in het hoofdstuk 'gravitatie'. Deze kracht wordt gegeven door:
$$ F_g = \frac{GMm}{r^2} $$Voor dit model willen we deze kracht opdelen in een x- en een y-component (zie de onderstaande afbeelding). Dit kunnen we doen met behulp van de sinus en de cosinus:
$$ \cos\alpha = \frac{\text{aanliggende zijde}}{\text{schuine zijde}} = \frac{F_{g,x}}{F_g} $$ $$ \sin\alpha = \frac{\text{overstaande zijde}}{\text{schuine zijde}} = \frac{F_{g,y}}{F_g} $$Deze formules kunnen we omschrijven tot:
$$ F_{g,x} = -F_g \cos\alpha $$ $$ F_{g,y} = -F_g \sin\alpha $$De mintekens zijn toegevoegd omdat de componenten naar links en naar beneden wijzen (die de onderstaande afbeelding).
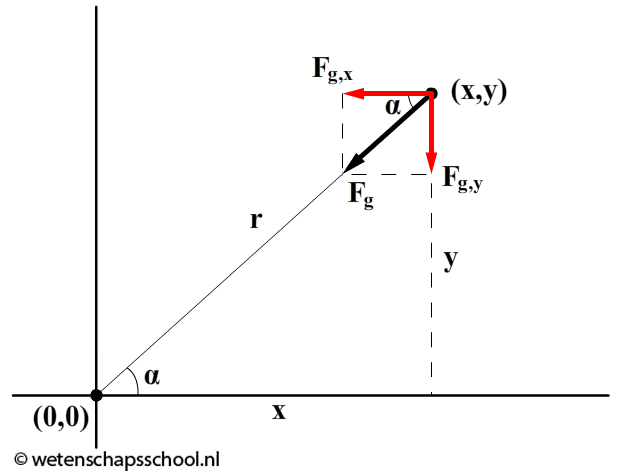
In de bovenstaande afbeelding kunnen we ook zien dat sin(α) = y/r en cos(α) = x/r. We kunnen hiermee de bovenstaande formules herschrijven tot:
$$ F_{g,x} = -F_g \frac{x}{r} $$ $$ F_{g,y} = -F_g \frac{y}{r} $$Met de tweede wet van Newton kunnen we nu voor beide componenten de versnelling uitrekenen:
$$ a_x = \frac{F_{g,x}}{m} $$ $$ a_y = \frac{F_{g,y}}{m} $$Met deze componenten van de versnelling kunnen we de nieuwe snelheid en positie van de planeet uitrekenen. Het volledige model staat hieronder gegeven:
Zoals je in het model kan zien, maakt de planeet een ellipsbaan om de ster. De planeten in ons zonnestelsel bewegen ook in ellipsbanen om de zon. In het hoofdstuk 'gravitatie' hebben we telkens aangenomen dat deze beweging bij benadering gelijk is aan een cirkelbaan.
 Modelleren met de gravitatiekracht
Modelleren met de gravitatiekracht
|
|