Hoofdstuk 2
Astrofysica

§1     Spectraalanalyse

In dit hoofdstuk gaan we eigenschappen van sterren bestuderen. Dit doen we door het licht afkomstig van deze sterren te analyseren. In deze eerste paragraaf gaan we met dit licht achterhalen uit welke stoffen sterren bestaan.

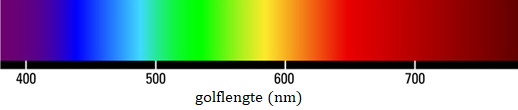
Als we licht van een gloeilamp door een prisma schijnen, dan krijgen we een volledige 'regenboog' aan kleuren te zien. We noemen dit een continu spectrum (zie de onderstaande afbeelding).

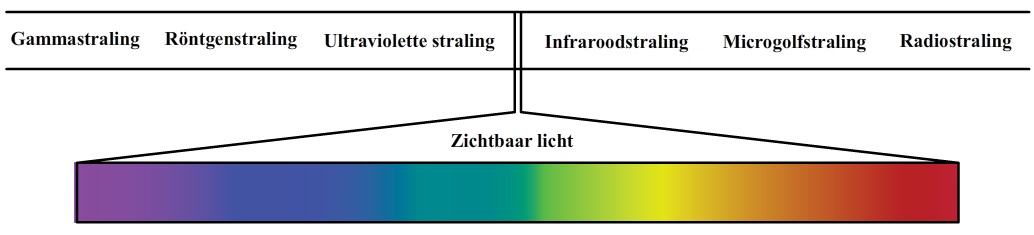
Naast het zichtbare deel van het spectrum, is er ook straling die we met onze ogen niet kunnen zien. Links van het paarse deel van het spectrum bevindt zich bijvoorbeeld ultravioletstraling, röntgenstraling en gammastraling. Rechts van het rode deel van het spectrum hebben we infrarood straling, microgolfstraling en radiostraling. Zoals je in de onderstaande afbeelding kan zien, is het zichtbare deel van het spectrum maar een klein deel van het gehele spectrum.

Licht bestaat uit kleine deeltjes die we fotonen noemen. Het verschil tussen verschillende kleuren licht zit hem in de frequentie (f) van de fotonen. Elk foton met een bepaalde frequentie heeft ook zijn eigen fotonenergie (E_f). Deze energie kan als volgt berekend worden:

$$E_f = hf$$ Energie (Ef) joule (J) Constante van Planck (h) 6,62606957 x 10-34 Js Frequentie van foton (f) hertz (Hz)

In het hoofdstuk trillingen hebben we gezien dat f = v/λ. Deze formule kunnen we ook toepassen op het foton. Als we voor de snelheid de lichtsnelheid (c) invullen, dan vinden we:

$$E_f = h\frac{c}{\lambda}$$ Energie (Ef) joule (J) Constante van Planck (h) 6,62606957 x 10-34 Js Lichtsnelheid (c) 2,99792458 x 108 m/s Golflengte van foton (λ) meter (m)

Als we licht van een gloeilamp op waterstof schijnen, dan zal het meeste licht hier dwars doorheen schijnen. Alleen licht met specifieke frequenties zal worden geabsorbeerd. Als gevolg worden er in het spectrum van het licht een aantal zwarte lijnen zichtbaar (zie de onderstaande afbeelding). We noemen dit absorptielijnen en het bijbehorende spectrum noemen we een absorptiespectrum.

Het geabsorbeerde licht wordt later in willekeurige richting weer uitgezonden. Het spectrum van dit licht is hieronder afgebeeld. We noemen dit een emissiespectrum en de lijnen worden spectraallijnen genoemd.  Zoals verwacht vinden we in dit spectrum alleen de frequenties licht die geabsorbeerd waren uit de lichtbron.

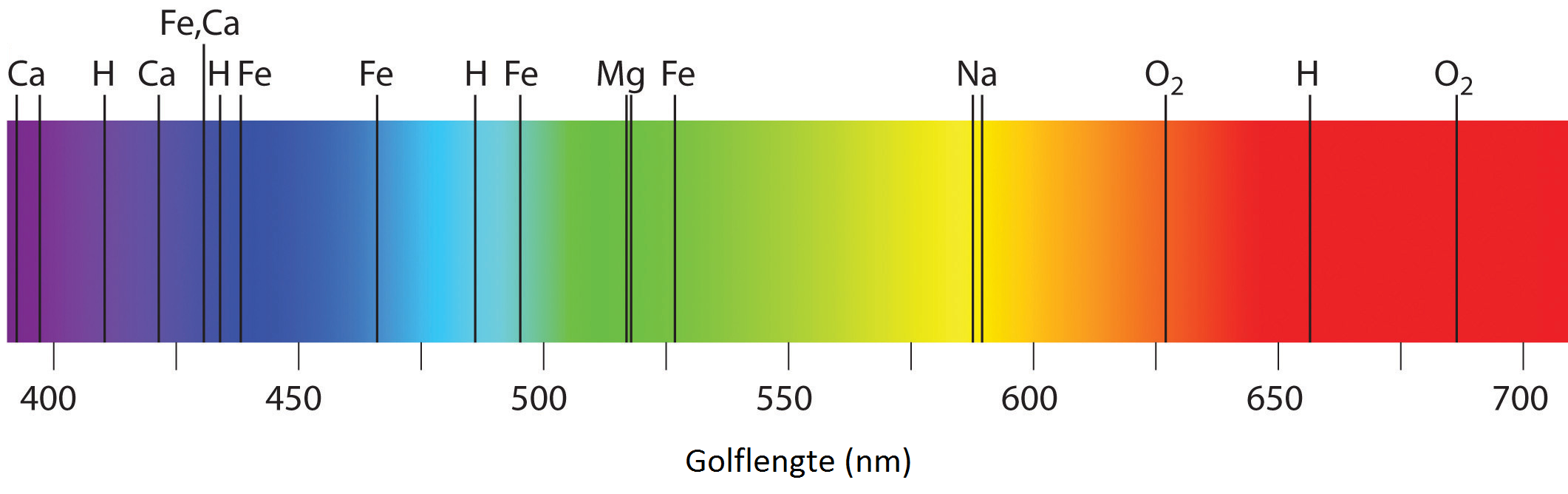
Elke stof heeft zijn eigen unieke spectrum van spectraallijnen. Als gevolg kunnen we aan de hand van het spectrum achterhalen door welke stoffen het licht geschenen is. Deze techniek wordt bijvoorbeeld gebruikt om te achterhalen uit welke stof de zon bestaat. In de kern van de zon wordt met behulp van kernfusie een continu spectrum aan licht geproduceerd. Als dit licht zich echter door de zon naar buiten werkt, worden een aantal frequenties geabsorbeerd. Hierdoor ontstaan spectraallijnen in het zonnespectrum. We noemen deze lijnen de Fraunhoferlijnen. Hieronder zien we de meest prominente absorptielijnen in het visuele gedeelte van het spectrum van de zon.

Voorbeeld

Vraag: Door een LED-lamp loopt een stroom van 50 mA. Sommige elektronen die door de LED stromen zorgen voor het uitzenden van een blauw foton met een golflengte van 470 nm. Het totale vermogen van het uitgezonden licht is 0,075 W. Bereken hoeveel procent van de elektronen een blauw foton heeft uitgezonden. Antwoord: Ten eerste kunnen we het aantal elektronen uitrekenen dat door de draad stroomt. In BINAS vinden we dat de lading van een elektron gelijk is aan e = 1,602 × 10-19 C. Daarnaast betekent een stroomsterkte van 0,050 A dat er 0,050 coulomb per seconde door de LED stroomt. Het totaal aantal elektronen dat per seconde door de LED stroomt, is dus gelijk aan: $$\frac{0,050}{1,602 \times 10^{-19}} = 3,12 \times10^{17} \text{ elektronen per seconde}$$ We kunnen ook uitrekenen hoeveel fotonen er per seconde vrijkomen. Hiervoor berekenen we eerst de energie van één blauw foton: $$E_f = h\frac{c}{\lambda}$$ $$E_f = 6,63\times 10^{-34}\times \frac{ 3,00\times 10^8}{470\times 10^{-9}}=4,23\times 10^{-19} \text{ J}$$ Een vermogen van 0,075 W vertelt ons dat er 0,075 joule per seconde aan licht vrijkomt. Hiermee kunnen we het aantal fotonen per seconde uitrekenen: $$\frac{0,075}{4,23\times 10^{-19}} = 1,8 \times 10^{17} \text{ fotonen per seconde}$$ Nu kunnen we uitrekenen hoeveel procent van de elektronen een blauw foton uitzendt: $$\frac{1,8 \times 10^{17}}{3,12 \times10^{17}} = 0,57 = 57 \text{ %}$$

Rekenen met de fotonenergie en redeneren met spectraallijnen

Bereken hoeveel minuten het duurt, voordat zonlicht de aarde bereikt. Bij een ruimtereis naar de maan is een reflector geplaatst op het maanoppervlak. Door een laser vanaf de aarde naar deze reflector te schieten, kan de afstand tot de maan gemeten worden. Het laserlicht doet er 2560 ms over totdat het terug is op aarde. Bereken hiermee de afstand tot de maan. Telefonie werkt met behulp van radiosignalen. Wat is de snelheid van deze radiosignalen. Sommige schepen hebben een radarinstallatie om de afstand tot voorwerpen in de omgeving te meten. Een radarinstallatie zendt hiervoor elektromagnetische signalen uit die weerkaatst worden door het voorwerp. Door de tijd tussen het uitzenden en het ontvangen van een signaal te meten, kan de afstand tot het voorwerp bepaald worden. Een veelgebruikt type radar is de pulsradar. Dit type radar zendt een kort elektromagnetisch signaal uit en ontvangt even later de echo van dit signaal. Op een bepaald moment wordt er 0,26 ms gemeten tussen het uitzenden en het ontvangen van een signaal. Bereken de afstand tot het voorwerp. Het signaal is een puls die bestaat uit een aantal opeenvolgende elektromagnetische golven. Deze golven worden gemaakt met een vaste frequentie van 9,38 GHz. Eén puls duurt 0,100 µs. Bereken uit hoeveel golven één puls bestaat. Details met afmetingen van 10% van de golflengte zijn door de pulsradar net waar te nemen. Bereken de minimale afmeting van een voorwerp dat met deze pulsradar waar te nemen is. (bron: examen HAVO 2018-1) Twee satellieten Grace A en B draaien achter elkaar aan om de aarde. Ze zijn een afstand van 220 km van elkaar verwijderd. Bereken hoe lang het duurt om een radiosignaal van de ene naar de andere satelliet te sturen. Grace A ontvangt continu een signaal van Grace B. De frequentie van de gebruikte radiosignalen bedraagt 32,7 GHz. Bereken de golflengte van het signaal. Het signaal van Grace A wordt in Grace B vergeleken met een eigen referentiesignaal van dezelfde frequentie. Als de afstand AB niet verandert, dan lopen deze twee signalen in fase. De frequentie van de gebruikte radiosignalen bedraagt 32,7 GHz.  Als de afstand AB groter wordt, ontstaat een faseverschil tussen het ontvangen signaal en het referentiesignaal.Op een gegeven moment is het faseverschil gelijk aan 0,015. Bereken het verschil in afstand AB bij dit faseverschil. (bron: examen VWO 2013-pilot) In het spectrum van natrium zijn twee duidelijke absorptielijnen te zien. De eerste lijn wordt veroorzaakt door fotonen met een golflengte van 589,0 nm en de andere door fotonen met een golflengte van 589,6 nm. Laat met behulp van BINAS zien welke kleur deze fotonen hebben. In de onderstaande afbeelding is het spectrum van een ster weergegeven: Leg uit of het hier gaat om een absorptie- of een emissiespectrum. Leg uit hoe de spectraallijnen in deze ster ontstaan zijn. De vier zichtbare spectraallijnen worden allemaal veroorzaakt door hetzelfde element. Ga met behulp van BINAS na om welk element het hier gaat. In de onderstaande afbeelding is het spectrum van een nevel weergegeven, waaruit sterren zich kunnen vormen: Leg uit of het hier gaat om een absorptie- of een emissiespectrum. Leg uit hoe de spectraallijnen in deze nevel ontstaan zijn. Leg uit hoe je kan zien dat in deze nevel geen waterstof aanwezig is. Een stilstaand elektron absorbeert een foton met een golflengte van 500 nm. Bereken de energie van het foton. Bereken de snelheid die het elektron hierdoor zal krijgen. Elk deeltje heeft zijn eigen anti-deeltje. Het anti-deeltje van het elektron is bijvoorbeeld het positron. Dit deeltje heeft exact dezelfde eigenschappen als het elektron, maar dan met een positieve lading. Als een elektron tegen een positron botst, dan worden beide deeltjes omgezet in twee dezelfde fotonen. De energie van deze fotonen is te berekenen met: $$E=mc^2$$ Bereken de frequentie van deze fotonen. Als geleidingselektronen door de LED stromen, botsen ze tegen de atomen in de LED. Als gevolg wordt blauw licht uitgezonden met een golflengte van 470 nm. Het totale vermogen aan uitgezonden licht gelijk is aan 0,075 W. Door een LED loopt een stroomsterkte van 50 mA. Bereken hoeveel procent van de geleidingselektronen dit blauwe licht heeft uitgezonden. (bron: examen VWO 2016-1)

§2     De planckkromme

Als atomen in een voorwerp trillen, dan zenden ze een heel spectrum aan straling uit. We noemen dit het planckspectrum. In deze paragraaf gaan we leren hoe we met behulp van dit spectrum de temperatuur van sterren kunnen bepalen.

In het hoofdstuk 'warmte' hebben we geleerd dat atomen met een temperatuur boven de 0 kelvin continu aan het trillen zijn. In dat hoofdstuk hebben we echter niet besproken dat trillende atomen straling uitzenden. Omdat zo goed als elk materiaal een temperatuur heeft boven de 0 K, kunnen we dus stellen dat zo goed als elk materiaal in het universum straling uitzendt. Meestal zit deze straling echter buiten het zichtbare spectrum. De aarde en ook wijzelf geven bijvoorbeeld voornamelijk infraroodstraling af.

Als de temperatuur van een voorwerp hoog genoeg wordt, dan komt er een moment dat de straling wel zichtbaar wordt. Dit zien we bijvoorbeeld in de onderstaande afbeelding. Een stuk metaal is hier sterk verwarmd en begint hierdoor te gloeien in het rode deel van het spectrum. De regenboog in de grafiek stelt het zichtbare deel van het spectrum voor.

Het licht dat op deze manier ontstaat heeft een karakteristiek stralingsspectrum, genaamd de planckkromme of het planckspectrum. Hieronder is dit spectrum voor een aantal temperaturen weergegeven. We geven dit spectrum hieronder weer met op de horizontale as de golflengte van de straling en op de verticale as de intensiteit van deze straling.

Bij een lage temperatuur zit de straling bijna volledig in het infrarode deel van het spectrum. Als gevolg kunnen we deze straling niet waarnemen met onze ogen. Als de temperatuur hoger wordt, dan komt er een moment dat er genoeg rood licht wordt geproduceerd, zodat we dit met onze ogen kunnen zien. Als we de temperatuur nog meer verhogen, dan komt er een moment dat er in het hele zichtbare spectrum veel licht wordt uitgezonden. Als we alle kleuren licht tegelijk in onze ogen krijgen, dan zien we dit als wit licht. Als de temperatuur nog hoger wordt, dan gaat op een gegeven moment het blauwe licht domineren.

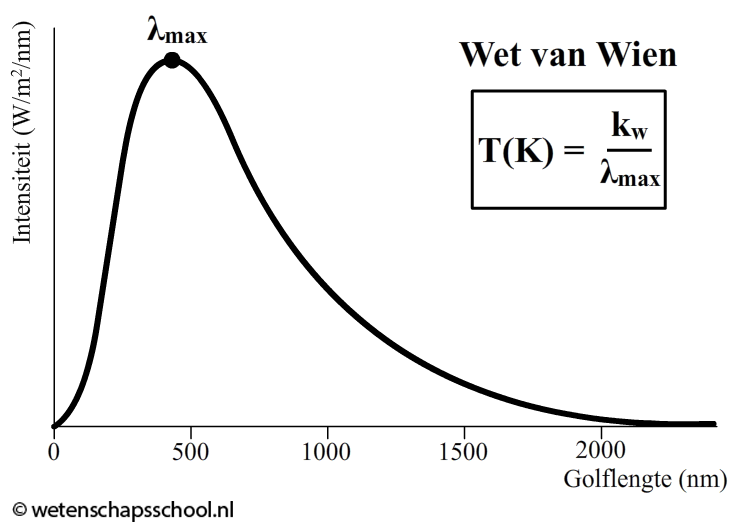
Hoe hoger de temperatuur van een object, hoe meer de piek van de planckkromme zich naar links verplaatst (naar een kleinere golflengte). Een blauwe ster heeft dus een hogere temperatuur dan een witte ster en een witter ster heeft een hogere temperatuur dan een rode ster. De relatie tussen de golflengte van de piek en de temperatuur noemen we de wet van Wien:

$$\lambda_{max} = \frac{k_w}{T}$$ Golflengte bij de piek (λmax) meter (m) Constante van Wien (kw) 2,8977721 x 10-3 Km Oppervlaktetemperatuur (T) kelvin (K)

De temperatuur moet in deze formule worden gegeven in kelvin. Er geldt:

$$T(K) = T(^\circ C) + 273$$

Met deze formule kunnen we bijvoorbeeld de oppervlaktetemperatuur van de zon berekenen. De piek van het stralingsspectrum van onze zon ligt bij de 500 nm. De oppervlaktetemperatuur is dus:

Met het oppervlak onder een planckkromme kunnen we de totale intensiteit van een lichtbron berekenen. In de onderstaande afbeelding is bijvoorbeeld alleen het zichtbare deel van een planckkromme afgebeeld. Als we de totale intensiteit van dit zichtbare gedeelte willen weten, dan willen de intensiteit van alle golflengtes in dit gebied bij elkaar optellen en dat is gelijk aan het oppervlak onder de grafiek.

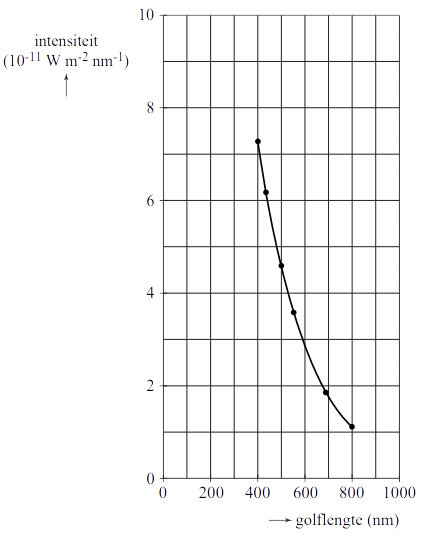
De SI-eenheid van de intensiteit (I) is W/m². Dit staat voor de hoeveelheid joule die per seconde op een vierkante meter valt. De intensiteit is te relateren aan het totale vermogen (P) dat een lichtbron uitzendt. We noemen het vermogen als het gaat om een lichtbron ook wel de lichtsterkte (L). Er geldt:

$$I = \frac{P_{bron}}{4\pi r^2} = = \frac{L}{4\pi r^2}$$ Intensiteit (I) watt per vierkante meter (W/m2) Vermogen van de bron (Pbron) watt (W) De lichtsterkte (L) watt (W) Straal vanaf het centrum van de bron (r) meter (m)

We zien aan de formule dat de intensiteit kwadratisch afneemt met de afstand tot de bron. We noemen deze formule daarom ook wel de kwadratenwet. In de onderstaande afbeelding is goed te zien waarom de intensiteit op deze manier afneemt. Hoe verder de straling komt, over hoe groter oppervlak de straling verdeeld wordt.

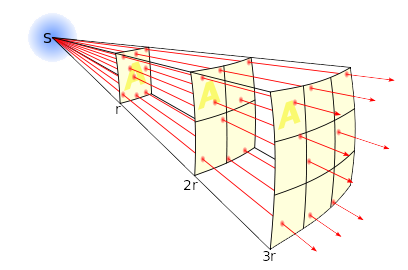
De intensiteit van de zon op aarde noemen we de zonneconstante. De waarde hiervan is te vinden in BINAS 32C. Ook de lichtsterkte van de zon is in deze tabel te vinden. We gebruiken voor de lichtsterkte van de zon het symbool L_☉.

We kunnen het vermogen (P) van een lichtbron ook relateren aan de oppervlaktetemperatuur (T). Deze relatie wordt de wet van Stefan-Boltzmann genoemd:

$$P_{bron} = L = \sigma A T^4 $$ Vermogen van de bron (Pbron) watt (W) Lichtsterkte (L) watt (W) De constante van Stefan-Boltzmann (σ) 5,670373 × 10-8 W/m2/K4 Oppervlak van de bron (A) vierkante meter (m2) Oppervlaktetemperatuur (T) kelvin (K)

Ter afsluiting nog een paar veelgebruikte afstandsmaten in de sterrenkunde. Afstanden in het zonnestelsel meten we vaak in astronomische eenheden (AE). 1 AE is gelijk aan de afstand van de aarde tot de zon, oftewel 1,49598 × 10¹¹ m. Afstanden tot sterren worden vaak gemeten in lichtjaar. Dit is de afstand die licht in een jaar aflegt, oftewel 9,461 × 10¹⁵ m. Beide afstanden kan je ook opzoeken in BINAS.

Rekenen met de wet van Wien

Welke gegevens van een ster kan je achterhalen met een absorptiespectrum? Hieronder zien we het spectrum van onze zon. Bepaal hieruit de oppervlaktetemperatuur van de zon in graden Celsius. Het menselijk lichaam zendt infraroodstraling uit. Laat met behulp van een schatting en een berekening zien dat dit het geval is. Bij een brandende gloeilamp heeft de gloeidraad een temperatuur van 2,5 × 103 K. Leg met een berekening uit waarom het rendement van een gloeilamp zo laag is. De temperatuur van een gloeidraad is te bepalen door het uitgezonden stralingsspectrum te vergelijken met de planck-kromme van dezelfde temperatuur. In de onderstaande figuren is de onderste kromme steeds van de gloeidraad en de bovenste kromme een planck-kromme. Leg uit in welke figuur de planck-kromme met dezelfde temperatuur als de gloeidraad staat. Bepaal de temperatuur van de gloeidraad in graden Celsius. (bron: examen VWO 2017-2) Van de ster Wega is de stralingsintensiteit in het zichtbare gebied als functie van de golflengte bepaald (zie de onderstaande afbeelding). Toon met behulp van het diagram aan dat de temperatuur van Wega hoger is dan 7000 K. De stralingsintensiteit die we van Wega meten is 2,9 × 10-8 Wm-2. Een percentage hiervan ligt in het zichtbare gebied. Bepaal dit percentage. (bron: examen VWO 2011-pilot) De WMAP doet metingen aan de zogenaamde kosmische achtergrondstraling. Dit is straling die overal in het universum te meten is. Hieronder zijn de metingen in een diagram weergegeven: Bereken de orde van grootte van de hoeveelheid fotonen met een golflengte tussen 1,0 en 2,0 mm, die per seconde op een vierkante meter terechtkomen. Bereken de temperatuur behorend bij de achtergrondstraling. (bron: examen VWO 2015-pilot)

Rekenen met de wet van Stefan-Boltzmann en de kwadratenwet

In een gloeilamp met een vermogen van 25 W zit een gloeidraad met een lengte van 25 mm en een diameter van 0,20 mm. Bereken de temperatuur van de gloeidraad. Een gloeilamp brandt eerst met een temperatuur van 2000 K en dan met 4000 K. Beredeneer met welke factor het vermogen is toegenomen. Op aarde ontvangen we maximaal 1,368 × 103 W/m2 aan licht van de zon. Dit wordt de zonneconstante genoemd. Gebruik de afstand tot de zon en reken hiermee uit hoeveel energie de zon per seconde omzet. De zon zendt per seconde 2,0 × 1038 neutrino's uit. Bereken hoeveel neutrino's er per seconde op de aarde terecht komen. De ster Wega heeft gemeten vanaf de aarde een intensiteit van 2,9 x 102 W/m2. Het uitgestraald vermogen van Wega is groter dan dat van de zon. Bereken hoeveel maal zo groot. Een ster met dezelfde kleur als de zon heeft een 81x zo grote lichtsterkte. Beredeneer hoeveel groter de diameter dan deze ster is ten opzichte van de zon. De ster Betelgeuze heeft ongeveer dezelfde temperatuur als de ster Proxima Centauri. Toch is Betelgeuze vanaf de aarde gezien 109x feller. Bereken hoeveel keer de straal van Betelgeuse groter is ten opzichte van Proxima Centauri.

§4     Dopplereffect

Als voorwerpen naar je toe bewegen of van de je af bewegen terwijl ze golven uitzenden, dan is een verandering in de frequentie van deze golven meetbaar. We noemen dit het dopplereffect. In deze paragraaf gaan we dit effect bestuderen.

In de onderstaande animatie zien we een voorwerp dat golven uitzendt. In de animatie op de website is een voorwerp te zien dat golven uitzendt. Als het voorwerp beweegt, dan kan je zien dat de golven in de bewegingsrichting dichter op elkaar zitten en de golven tegen de bewegingsrichting in verder van elkaar af. Als je de golven ontvangt als het voorwerp naar je toe beweegt, dan zal je dus een kleinere golflengte en een grotere frequentie meten. Als je de golven ontvangt als het voorwerp van je af beweegt, dan zal je dus een grotere golflengte en een kleinere frequentie meten. Dit wordt het dopplereffect genoemd. In het dagelijks leven merken we dit effect bijvoorbeeld als een ambulance met sirene langsrijdt. De toon klinkt hoger als de ambulance naar je toe rijdt en lager als de ambulance van je wegrijdt.

Ook bij licht kunnen we het dopplereffect meten. Voor zichtbaar licht zorgt dit voor een kleine kleurverandering. Als een lichtbron naar je toe komt, dan wordt de golflengte kleiner en als gevolg schuift het licht meer op naar de blauwe kant van het spectrum. We noemen dit blauwverschuiving. Als een lichtbron van je af beweegt, dan wordt de golflengte groter en als gevolg schuift het licht meer op naar de rode kant van het spectrum. We noemen dit roodverschuiving.

Dit effect is nauwkeurig te meten door naar de verplaatsing van de absorptielijnen te kijken. Deze schuiven namelijk ook mee met het spectrum. Dit zien we bijvoorbeeld in het onderstaande spectrum:

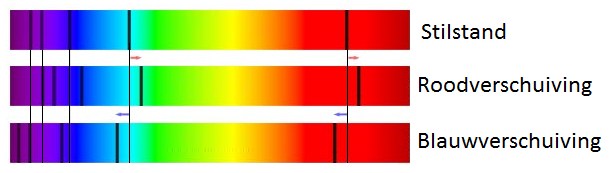
Door te meten hoeveel de spectraallijnen verplaatst zijn, kunnen we de snelheid bepalen waarmee lichtbronnen van ons af of naar ons toe bewegen. Er geldt:

$$v_{rad} = \frac{\Delta \lambda}{\lambda_0}c $$ De radiële snelheid van het voorwerp (vrad) meter per seconde (m/s) Toename van de golflengte (Δλ) meter (m) De oorspronkelijke golflengte (λ0) meter (m) Snelheid van het licht (c) 3,0 × 108 m/s

Let er op dat we met deze formule alleen de component van de snelheid berekenen waarmee een lichtbron van ons af of naar ons toe beweegt. We noemen deze component ook wel de radiële snelheid (zie de onderstaande afbeelding). Zijwaartse beweging van een ster kunnen we met het dopplereffect dus niet waarnemen.

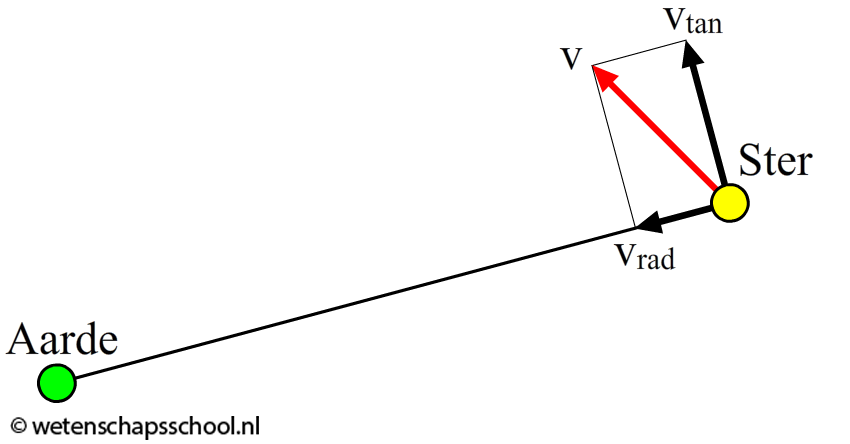
Voorbeeld

De helft van de sterren die we 's nachts zien blijken bij nadere inspectie dubbelsterren te zijn (twee sterren die om elkaar heen draaien). De sterren zitten in sommige gevallen zo dicht bij elkaar dat we ze zelfs met een telescoop niet direct van elkaar kunnen onderscheiden. Dankzij het dopplereffect kunnen we dit onderscheid wel maken. Als twee sterren om elkaar heen draaien, dan kan het zijn dat telkens de ene ster naar de aarde toe beweegt en de andere ster van de aarde af (zie de onderstaande linker afbeelding). Dankzij het dopplereffect zien we dan telkens twee absorptielijnen, waar we er normaal maar één zouden verwachten. De ene is door roodverschuiving de ene kant op verschoven en de andere is door blauwverschuiving de andere kant op verschoven. In het rechter diagram zijn de posities van twee van deze absorptielijnen in de tijd weergegeven: Vraag a: Op sommige momenten staan beide absorptielijnen in het diagram op dezelfde plek. Leg uit wanneer dit gebeurt. In de onderstaande situatie beweegt geen van de sterren van de aarde af of naar de aarde toe. De radiële snelheid is hier dus nul en als gevolg is er voor beide sterren geen dopplereffect te meten. Op deze momenten zijn beide absorptielijnen dus op hun oorspronkelijke locatie te vinden. Vraag b: Geef een moment aan in het diagram dat overeenkomt met de positie van de sterren zoals links naast het diagram is afgebeeld. In deze positie is de snelheid van beide sterren volledig radieel (ster A beweegt naar de aarde toe en ster B beweegt van de aarde af). De radiële snelheid is op dat moment dus maximaal en het dopplereffect is hier dus ook maximaal. Ster A beweegt naar de aarde toe. De golflengte van het signaal dat op aarde aankomt zal hier dus maximaal verkleint zijn. Dit gebeurt o.a. op tijdstip t = 0 s. Vraag c: Bereken met het diagram de baanstraal van ster A. Eerst berekenen we de snelheid van ster A: $$v_A = \frac{\Delta \lambda}{\lambda}c$$ $$v_A = \frac{410,21 - 410,17}{410,17}\times 3,0\times 10^8 = 2,9 \times 10^4 \text{ m/s}$$ De trillingstijd kunnen we aflezen uit het diagram (T = 1,4 × 106 s). Met deze trillingstijd kunnen we de baanstraal berekenen: $$v = \frac{2\pi r}{T}$$ $$r = \frac{vT}{2\pi}$$ $$r_A =\frac{2,9 \times 10^4 \times 1,4 \times 10^6}{2\pi} = 6,5 \times 10^9 \text{ m}$$

Als we naar verre melkwegstelsels kijken, dan blijken deze eigenlijk allemaal roodverschoven te zijn. Verre melkwegstelsels bewegen dus allemaal van ons af. Ook geldt dat hoe verder deze stelsels van ons af staan, hoe sneller ze van ons af bewegen. Wetenschapper Edwin Hubble concludeerde uit deze metingen dat het heelal aan het uitdijen is. Met behulp van Einsteins algemene relativiteitstheorie werd duidelijk dat het de ruimte zelf is die uitzet en alle melkwegstelsels uit elkaar drijft. Als licht zich door een uitdijende ruimte beweegt, wordt het opgerekt. De golflengte neemt hierdoor toe en het licht wordt daardoor roder.

Het feit dat melkwegstelsels van elkaar af bewegen, wil zeggen dat ze vroeger veel dichter bij elkaar zaten. De ruimte was vroeger dus ook veel kleiner. Wetenschappers denken nu dat de hele ruimte ooit vanuit één punt ontstaan is. Deze theorie wordt de oerknal genoemd.

Rekenen en redeneren met het dopplereffect

Een ambulance met sirene rijdt eerst in jouw richting en rijdt dan van je weg. Leg in beide situaties uit hoe de frequentie, de toonhoogte en de trillingstijd van het waargenomen geluid verandert. Leg uit wanneer roodverschuiving en blauwverschuiving plaatsvindt. Leg uit of je blauw- of roodverschuiving verwacht door de uitdijing van het heelal. Een gaswolk beweegt met grote snelheid door de ruimte. Het UV-licht dat door deze wolk uitgezonden wordt, wordt op aarde als paars licht waargenomen. Leg uit of we hier te maken hebben blauw- of roodverschuiving. Leg uit of de gaswolk van ons af of naar ons toe beweegt. Een spectraallijn van calcium bevindt zich bij stilstand op 393,3 nm. In een ver melkwegstelsel is deze lijn verschoven naar de 392,0 nm. Leg uit of dit melkwegstelsel van ons af of naar ons toe beweegt. Bereken de radiële snelheid van dit melkwegstelsel. Een leerling beweert dat de kans groot is dat de werkelijke snelheid van het melkwegstelsel hoger ligt dat de snelheid die in de vorige vraag berekend is. Leg uit dat deze leerling gelijk heeft. In de onderstaande afbeelding is een deel van het spectrum van de ster Arcturus en van de zon te zien. Leg uit of Arcturus van ons af of naar ons toe beweegt. Bereken hiermee de radiële snelheid van Arcturus. Sommige melkwegstelsel bevatten veel hete gassen die zorgen voor emissielijnen. We zien dit bijvoorbeeld in de onderstaande afbeelding. De lijn H-α is de eerste lijn uit de balmerserie van waterstof. Deze lijn is in het lab te vinden bij de 656 nm. Bereken de radiële snelheid van de gassen in dit melkwegstelsel. Met hoeveel procent van de lichtsnelheid beweegt dit melkwegstelsel van ons af? De meeste sterren roteren om hun as. Dit heeft als gevolg dat de spectraallijnen van deze sterren breder worden. Leg uit hoe dit komt. Een spectraallijn heeft in het lab een golflengte van 12,0000 cm. Dezelfde spectraallijn wordt gevonden in het spectrum van een melkwegstelsel. Aan de linkerkant van dit melkwegstelsel zit de lijn bij 21,1588 cm, in het midden bij 21,1536 cm en aan de rechter kant bij 21,1484 cm. Leg uit dat deze gegevens doen suggereren dat het melkwegstelsel roteert om zijn eigen as. Bereken de radiële snelheid waarmee dit melkwegstelsel in zijn geheel van ons af beweegt. Bereken de radiële rotatiesnelheid van het melkwegstelsel. Als twee sterren om elkaar heen draaien, dan kan het zijn dat telkens de ene ster naar de aarde toe beweegt en de andere ster van de aarde af (zie de onderstaande linker afbeelding). Dankzij het dopplereffect zien we dan telkens twee absorptielijnen, waar we er normaal maar één zouden verwachten. In het rechter diagram zijn de posities van twee absorptielijnen in de tijd weergegeven: Leg uit waarom er twee absorptielijnen zichtbaar zijn. Op sommige momenten staan beide absorptielijnen in het diagram op dezelfde plek. Leg uit wanneer dit gebeurt. Geef een moment aan in het diagram dat overeenkomt met de positie van de sterren zoals links naast het diagram is afgebeeld. Bereken met het diagram de baanstraal van ster A. Maak hiervoor o.a. gebruik van: $$v_{baan} = \frac{2\pi r_{baan}}{T}$$

§5     Het HR-diagram

In deze paragraaf bestuderen we het spectrum dat afkomstig is van sterren. Met informatie uit dit spectrum kunnen we een zogenaamd Hertzsprung-Russell diagram maken. In dit diagram is de evolutie van sterren goed zichtbaar.

Als we een diagram maken waarin we de temperatuur en de lichtsterkte van sterren tegen elkaar uitzetten, dan vinden we vast patroon. Dit diagram is hieronder afgebeeld en wordt het Hertzsprung-Russell diagram genoemd. Op de horizontale as staat de logaritme van de temperatuur (log(T)). De inverse van de logaritme is de tienmacht. Als we bijvoorbeeld een ster aflezen bij log(T) = 4,0, dan vinden we als volgt de bijbehorende temperatuur:

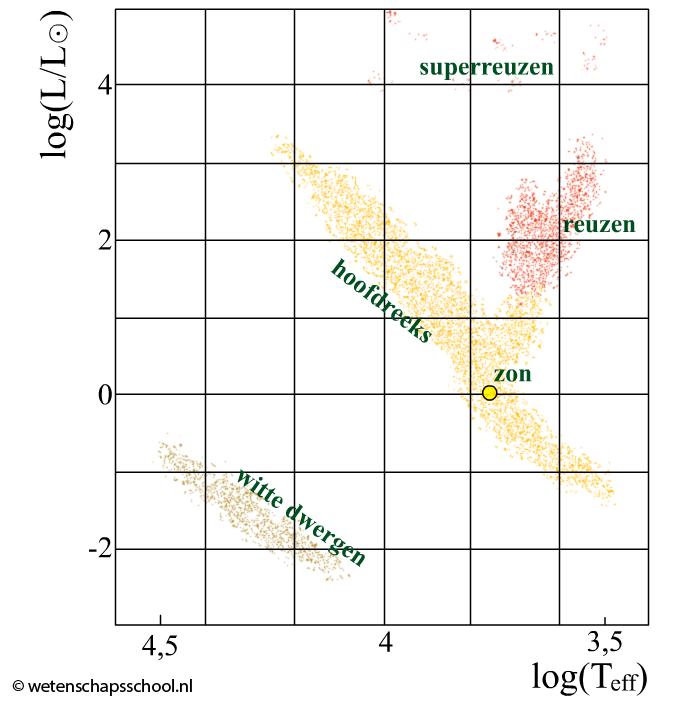
Op de verticale as staat log(L/L_☉). L/L_☉ is de lichtsterkte van de ster gedeeld door de lichtsterkte van de zon en geeft dus aan hoeveel de lichtsterkte groter is dan de zon. Als we een ster aflezen bij log(L/L_☉) = 2,6, dan vinden we:

Deze ster heeft dus een intensiteit die 4,0 × 10² keer zo groot is als de zon.

De zon is begrijpelijker wijs getekend bij log(L/L_☉) = 0. Hier geldt namelijk:

We vinden hier een resultaat dat we hadden kunnen verwachten. De lichtsterkte van de zon is gelijk aan 1x de lichtsterkte van de zon.

In het diagram kunnen we ook de straal van de sterren aflezen. Ook dit werkt met een logaritmische schaal:

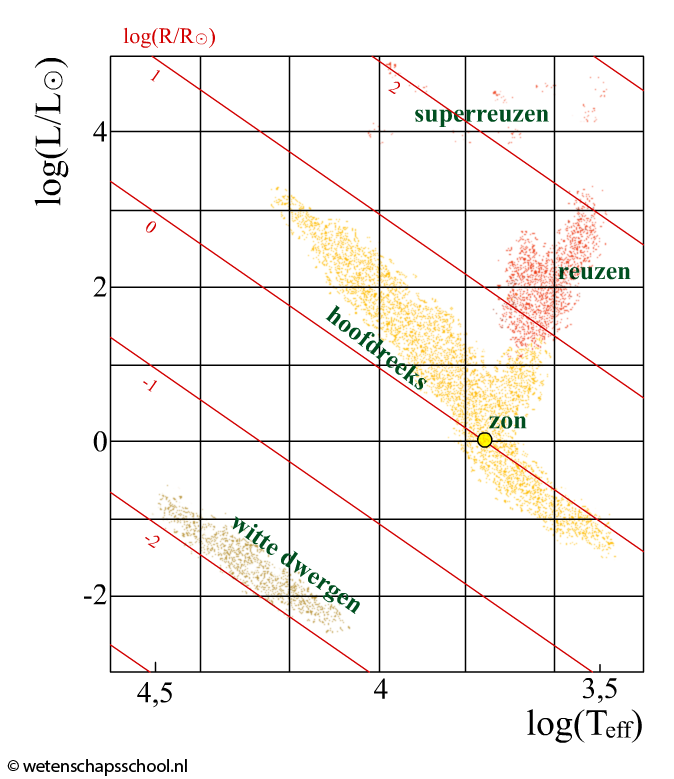
Stel een ster bevindt zich op log(R/R_☉) = 1,2, dan geldt er:

Deze ster heeft dus een straal 16x zo groot als de straal van de zon.

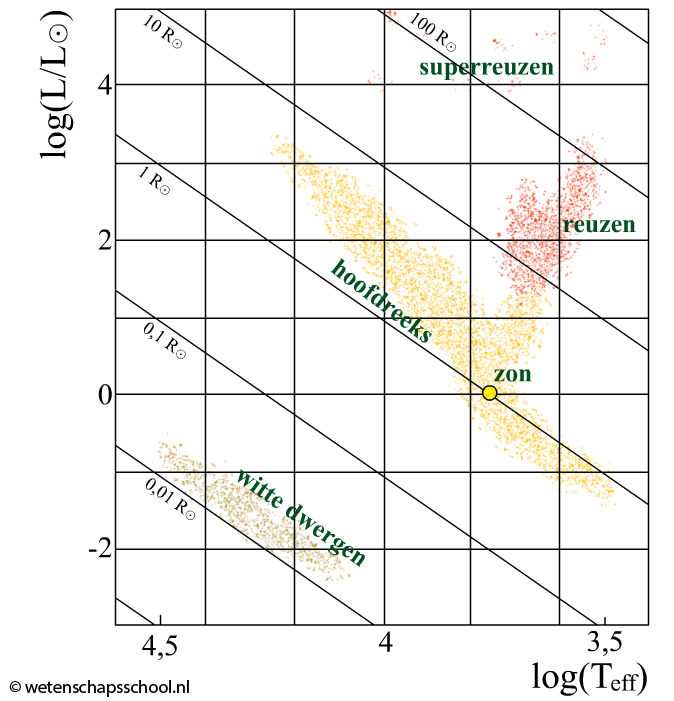
Let erop dat deze logaritmische schaal in BINAS is weergegeven zoals hieronder is weergegeven. Let er echter op dat de bovenstaande notatie nodig is om de straal van een ster af te lezen tussen de lijnen in.

Sterren in verschillende fase van hun ontwikkeling zijn te vinden op verschillende plekken in het diagram. Sterren ontstaan uit grote gas- en stofwolken die we nevels noemen. Als de ster eenmaal stabiel is, zit hij in de zogenaamde hoofdreeks. Ook de zon bevindt zich, samen met 90% van de sterren, in deze hoofdreeks.

Gedurende deze fase wordt waterstof in de kern van de ster gefuseerd tot helium. Als het waterstof op is, stort de ster in elkaar. Dit zorgt voor een enorme toename van de temperatuur waardoor helium in de kern kan fuseren tot koolstof en zuurstof. Hier komt zoveel energie bij vrij, dat de ster enorm uitzet. Door het extreme uitzetten koelt de ster zo ver af dat deze rood licht gaat uitzenden. Een lichte ster noemen we in deze fase een rode reus en een zware ster noemen we in deze fase een rode superreus (zie het bovenstaande diagram en de onderstaande afbeelding).

Als ook de helium opraakt, stort de ster geheel in elkaar. Bij een lichte ster, zoals de zon, wordt de kern in elkaar gedrukt tot een klein zwaar object dat een witte dwerg wordt genoemd. De buitenste lagen schieten naar buiten en worden een planetaire nevel genoemd.

Als een superreus ineenstort, is de implosie veel krachtiger. Nu wordt de kern ineengedrukt tot een neutronenster (waarin alle protonen en elektronen zijn samengedrukt tot neutronen) of een zwart gat (een object dat zo zwaar is dat zelfs licht er niet aan kan ontsnappen). De buitenste lagen worden met enorm veel energie de ruimte ingeschoten. Dit wordt een supernova genoemd.

Aflezen van het HR-diagram

We bestuderen de ster Aldebaran in het Hertzsprung-Russell diagram. Bereken met behulp van het diagram de temperatuur van de ster. Bereken met behulp van het diagram de lichtsterkte van de ster ten opzichte van de zon. Bereken met behulp van het diagram de straal van de ster ten opzichte van de zon. We bestuderen de ster Sirius in het Hertzsprung-Russell diagram. Bereken met behulp van het diagram de temperatuur van de ster. Bereken met behulp van het diagram de lichtsterkte van de ster ten opzichte van de zon. Bereken met behulp van formules uit BINAS de straal van de ster. Kijk daarna of deze waarde overeenkomt met de waarde in het Hertzsprung-Russell diagram.

§3     Draadloze communicatie

Radiostraling kan worden gebruikt voor draadloze communicatie. Denk bijvoorbeeld aan telefonie en wifi. In deze paragraaf gaan we dit type communicatie bestuderen.

Draadloze communicatie werkt met behulp van radiogolven. Dit type straling wordt bijvoorbeeld gebruikt voor satelliet tv, mobiele telefoons en wifi. Net als geluid, heeft radiostraling als voordeel dat het een relatief grote golflengte heeft en als gevolg gemakkelijk om obstakels heen buigt. Als gevolg zijn radiogolven zelfs met veel obstakels in de buurt goed te ontvangen. Dit is niet het geval bij zichtbaar licht, omdat dit een veel kleinere golflengte heeft. Daarnaast kunnen radiogolven, net als geluidgolven, ook door muren heen. Ten opzichte van geluid, hebben radiogolven het voordeel dat ze een groter bereik hebben en ook in vacuüm (dus in de ruimte) gebruikt kunnen worden.

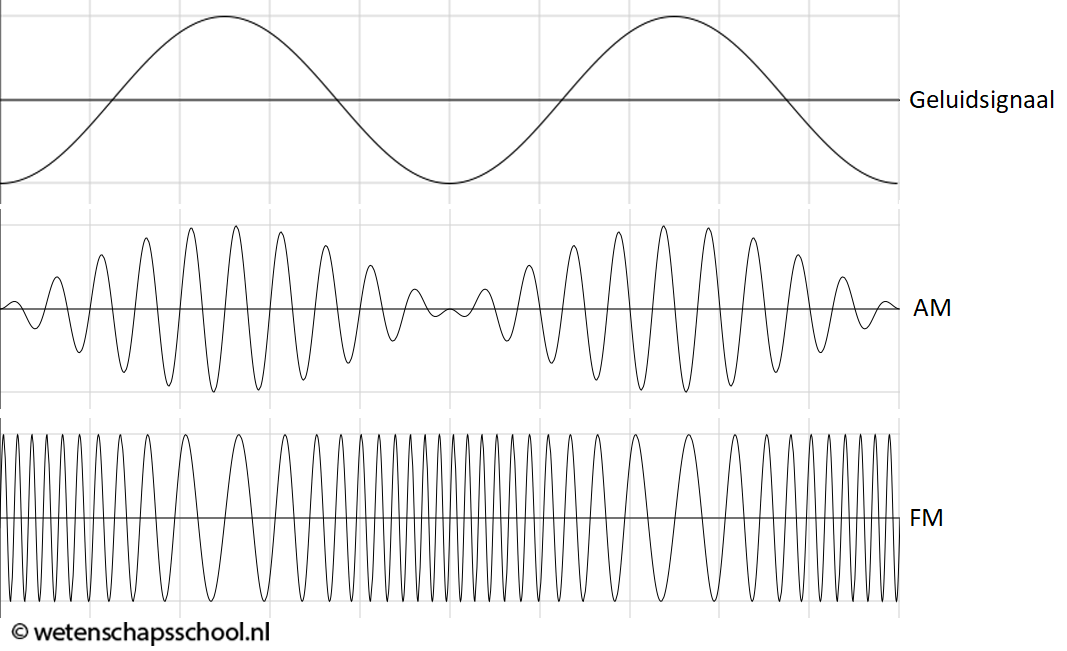
Door de vorm van een radiogolf aan te passen, kunnen we er informatie in verstoppen. Stel dat we bijvoorbeeld een telefoongesprek willen versturen. In dat geval moeten we de geluidsgolven van het gesprek verstoppen in het radiosignaal. De simpelste manier waarop we dit kunnen doen is door de amplitude van de radiogolf aan te passen, zodat het radiosignaal gaat lijken op het oorspronkelijke geluidssignaal. We noemen dit amplitudemodulatie (AM). Het resultaat hiervan is te zien in de onderstaande afbeelding. Een andere methode is door niet de amplitude, maar de frequentie van de radiogolf te variëren. We spreken in dit geval van frequentiemodulatie (FM). In het onderstaande voorbeeld zien we dat hoe hoger de grafiek van het oorspronkelijke signaal is, hoe kleiner de frequentie van het FM-signaal is.

Met het menselijk oor kunnen we tot ongeveer een frequentie van 20 kHz horen. Als we muziek willen versturen, dan moeten we daar dus een frequentiegebiedje van 20 kHz voor reserveren. We zeggen dan dat het verstuurde signaal een bandbreedte heeft van 20 kHz.

De oorspronkelijke radiogolf noemen we de draaggolf. Stel we hebben een draaggolf van 45000 kHz (45 MHz). Als we een signaal met een bandbreedte van 20 kHz aan de draaggolf toevoegen, dan bestrijkt het uiteindelijke signaal een frequentiegebiedje van 45000 + 10 = 45 010 kHz tot 45000 - 10 = 44990 kHz.

Omdat er continu meerdere signalen worden verstuurd en we niet willen dat deze signalen met elkaar interfereren, moet elk signaal zijn eigen frequentiegebiedje hebben. Dit wordt kanaalscheiding genoemd en elk frequentiegebiedje wordt een kanaal genoemd.

De geluidsignalen die we tot nu toe hebben besproken zijn analoog. We kunnen hier echter ook digitale signalen van maken, bestaande uit een reeks enen en nullen. Als we een 1 willen versturen, dan zetten we het radiosignaal aan en willen we een nul versturen, dan zetten we het radiosignaal uit. We noemen dit het digitaliseren van een signaal.

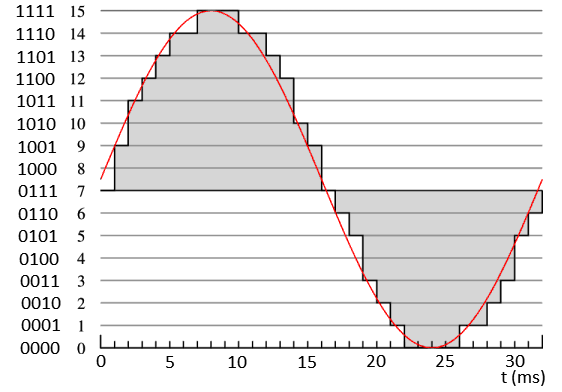
Elke 0 of 1 in deze reeks wordt een bit genoemd. Een signaal van één bit kan maar twee waarden aannemen (0 of 1). Een signaal van twee bit kan wel vier waarden aannemen (00, 01, 10, 11). Een signaal van n bit, kan 2ⁿ waarden aannemen. Een signaal van 4 bit kan dus 2⁴ = 16 waarden aannemen. Als we een geluidsgolf digitaal willen versturen in 4 bit, dan delen we deze golf verticaal op in 16 stukjes met elk een eigen binaire code (zie de onderstaande afbeelding). Om de zoveel tijd wordt dan de binaire code verstuurd die de geluidsgolf het dichtst benadert.

De binaire code moet ook verzonden en ontvangen worden en ook dit kost tijd. Het aantal bits dat per tijdseenheid verzonden kan worden, noemen we de datatransfer rate. Het wordt uitgedrukt in bits per seconde (bps).

Vaak wordt naast bit ook de eenheid byte gebruikt. Een byte is gelijk aan 8 bits.

Redeneren met AM en FM

Een radiozender zendt het onderstaande signaal uit. Leg uit of dit een AM of FM signaal is. Hieronder zien we een signaal van een breedbandradar uitgezet tegen de tijd. Geef aan of hier sprake is van frequentiemodulatie of van amplitudemodulatie. (bron: examen HAVO 2018-1) Hieronder is een gemoduleerd signaal weergegeven: Bepaal de frequentie van de draaggolf. Bepaal de frequentie van het signaal waarmee de draaggolf is gemoduleerd.

Rekenen met kanaalscheiding en datatransfer

Radiozenders op de FM zenden uit op frequenties tussen 87,50 MHz en 108,00 MHz. Reken uit hoeveel kanalen met een bandbreedte van 200 kHz in dit frequentiegebied passen. De ruimtesonde Pioneer-10 kan met de aarde communiceren via radiocommunicatie. Hiertoe zendt men vanaf de aarde een draaggolf van 2,11 GHz uit (uplink) met een bandbreedte van 40 MHz. De ruimtesonde vermenigvuldigt de frequentie dan met een factor 240 / 221 en zendt het signaal daarna terug (downlink). De factor zorgt ervoor dat de uplink- en de downlink-signalen in gescheiden kanalen zitten. Leg uit waarom dit belangrijk is. Toon met een berekening aan dat de kanalen inderdaad gescheiden zitten. (bron: examen VWO 2011-pilot) Een erg kleine antenne kan signalen met 2,0 × 104 bits per seconde verzenden. Een digitale foto bevat 5 megabyte (MB) aan informatie. In het dataverkeer is 1 byte gelijk aan 8 bits. Bereken hoeveel uur het zou duren om de foto te verzenden. Leg uit dat een hogere bemonsteringsfrequentie over het algemeen zorgt voor een nauwkeuriger signaal. Leg uit dat een hogere bemonsteringsfrequentie op een gegeven moment niet meer helpt als het aantal bits te klein is. Leg uit dat een hoger aantal bits over het algemeen zorgt voor een nauwkeuriger signaal. Leg uit dat een hoger aantal bits op een gegeven moment niet meer helpt als de bemonsteringsfrequentie te klein is. Het uploaden van een bestand van 128 MB naar de cloud kost 45 seconden. Bereken de datatransfer rate. De 'American Standard Code for Information Interexchange' (ASCII) bestaat uit 128 binaire gecodeerde karakters. Deze codes worden voor tekst in computers gebruikt. Bereken het aantal bits dat per karakter nodig is. Een computer genereert 125.000 karakters per seconde. Bereken de datatransfer rate. Een leerling stuurt een afbeelding van 20 MB door naar een klasgenoot. De internetverbinding heeft een snelheid van 15 Mbps. Bereken hoe lang het duurde om het bestand weg te sturen. Een webcam maakt video's van 1920 bij 1080 pixels, met 8 bits per pixel. De webcam maakt 20 frames per seconde. Bereken de datatransfer rate.