Hoofdstuk 2
Radioactiviteit
§1 De bouw van atomen
In dit hoofdstuk gaan we bestuderen wat radioactiviteit precies is en wat de gevaren zijn. Ook gaan we een aantal medische toepassingen bestuderen. Voordat we dit alles kunnen begrijpen, moeten we eerst atoomkernen bestuderen. Dat gaan we in deze eerste paragraaf doen.
Atomen bestaan uit allerlei kleine deeltjes. Elk atoom heeft in zijn centrum een atoomkern, bestaande uit positief geladen deeltjes die we protonen (p) noemen en neutraal geladen deeltjes die we neutronen (n) noemen. Om de kern heen bevindt zich een wolk van negatieve deeltjes die we elektronen (e) noemen. Een atoom is altijd neutraal en bevat dus evenveel protonen als elektronen. Als het aantal protonen en elektron niet gelijk is, dan spreken we niet van een atoom, maar van een ion.
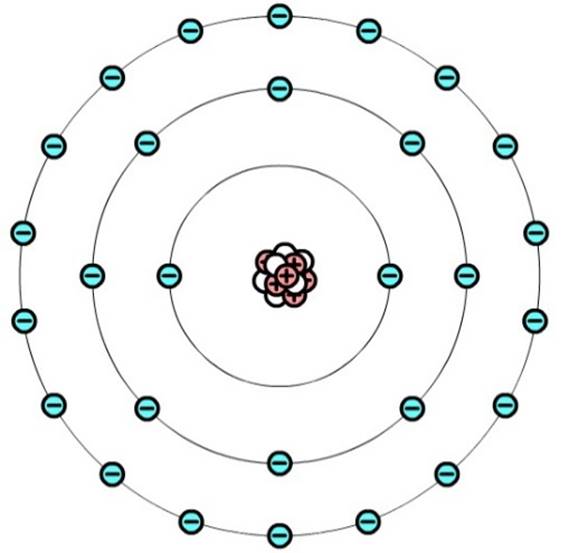
De materie om ons heen bestaat uit 118 soorten atomen. De symbolen behorende bij deze 118 atoomsoorten vinden we in de onderstaande tabel. We noemen dit het periodiek systeem.

Elk atoomsoort wordt gekenmerkt door een vast aantal protonen in de kern. Het aantal protonen in de kern wordt ook wel het atoomnummer genoemd. In het periodiek systeem staat het atoomnummer linksonder elk element genoemd.
Hieronder zien we de eerste 8 atomen uit het periodiek systeem. Waterstof heeft een atoomnummer van 1 en heeft dus 1 proton in de kern. Om hier een neutraal atoom van te maken moet er ook één elektron om de kern bewegen. Helium heeft een atoomnummer van 2 en heeft dus twee protonen in de kern en dus ook twee elektronen om de kern heen. Etc.

Het aantal protonen en neutronen samen noemen we het massagetal. Het massagetal wordt vaak achter de naam van het element genoemd. Fluor-19 heeft dus een massagetal van 19. Omdat fluor volgens het bovenstaande periodiek systeem 9 protonen heeft, moet het dus ook nog 10 neutronen bevatten (omdat 9 + 10 = 19). Waterstof-1 heeft een atoomnummer van 1 en bevat dus slechts 1 proton. Het massagetal van waterstof is ook 1, dus waterstof bevat 0 neutronen (omdat 1 + 0 = 1).
Het massagetal wordt ook geregeld linksboven het symbool van het element genoemd. Het atoomnummer en massagetal schrijven we dan als volgt op:
$$^{\;\;\;\text{ massagetal}}_{\text{atoomnummer}}\text{Element}$$
De massagetallen staan niet in het periodiek systeem genoemd en daar is een goede reden voor. Het massagetal van een atoomsoort staat namelijk niet vast. Zo heb je bijvoorbeeld koolstof-12 en koolstof-14. In het periodiek systeem kunnen we zien dat koolstof altijd 6 protonen in de kern heeft. Om op het juiste massagetal uit te komen moet koolstof-12 nog 6 neutronen in de kern hebben (want 6 + 6 = 12) en moet koolstof-14 nog 8 neutronen in de kern hebben (want 6 + 8 = 14).
Atomen met hetzelfde aantal protonen, maar met een verschillend aantal neutronen noemen we isotopen. Koolstof-12 en koolstof-14 zijn dus twee isotopen van koolstof.
$$^{12}_{\;6}C \;\;\;\;\;\; ^{14}_{\;6}C$$
Ook het proton, het neutron en het elektron kunnen we in deze notatie opschrijven. Het proton bestaat uit 1 proton 0 neutronen, dus het atoomnummer is 1 en het massagetal is ook 1. Het neutron bestaat uit 0 protonen en 1 neutron, dus het atoomnummer is 0 en het massagetal is 1. Het elektron vormt een uitzondering op de regel. Een elektron bevat natuurlijk 0 protonen, maar omdat het een lading van -1 heeft, zeggen we dat het atoomnummer -1 heeft. Het massagetal van een elektron is 0.
|
… $$^1_1p \;\;\;\;\;\;\;\; ^1_0n \;\;\;\;\;\;\;\; ^{\;\;0}_{-1}e$$
|
|
|
|
1. Alledaagse voorwerpen als stoelen en tafels bestaan uit geladen deeltjes zoals protonen en elektronen. Hoe komt het dat we hier in de praktijk niks van merken?
2. Een atoom bevat 16 protonen. Om welk soort atoom gaat het hier?
3. Een atoom bevat 79 protonen. a. Hoeveel elektronen bevat dit atoom? Leg je keuze uit. b. Welke atoomsoort is dit?
4. Teken een magnesium-24 atoom. Geef hierin duidelijk de protonen, de neutronen en de elektronen weer.
5. Reken bij de volgende atomen uit hoeveel protonen en hoeveel neutronen er in de atoomkern zitten: a. Helium-4 b. Koolstof-14 c. IJzer-56 d. Waterstof-1 6. Hoeveel protonen bevat één watermolecuul?
7. Een atoom X heeft atoomnummer 35 en massagetal 79. Een ander atoom Y heeft een massagetal van 81. Beide atomen zijn isotopen van elkaar Hoeveel protonen, neutronen en elektronen zitten er in atoom X en Y?
|
§2 Kernverval
In deze paragraaf gaan we onze kennis over atoomkernen uit de vorige vraag gebruiken om kernreacties te beschrijven.
In deze paragraaf bespreken we kernreacties. We spreken van een kernreactie als de atoomkern een verandering ondergaat. Een voorbeeld van een kernreactie is kernverval. Dit is het spontaan uit elkaar vallen van een atoomkern. Stoffen waarbij dit gebeurt noemen we radioactief. Bij kernverval schiet er vaak een deeltje met behoorlijke snelheid uit het atoom weg. We noemen dit straling. Als een atoom straling uitgezonden heeft, dan zeggen we dat het atoom vervallen is. De oorspronkelijke radioactieve kern noemen we de moederkern en de kern die na de straling overblijft noemen we de dochterkern. In sommige gevallen zijn de dochterkernen zelf ook weer radioactief. Er bestaan ook atoomkernen die geen straling uitzenden. We noemen deze isotopen stabiel.
Het is belangrijk goed onderscheid te maken tussen kernreacties en chemische reacties. Bij een chemische reactie worden elektronen tussen atomen uitgewisseld of gedeeld. De kernen van de atomen blijven bij chemische reacties onaangetast. Bij kernreacties is het juist de kern die verandert.
Er kunnen bij kernreacties een aantal soorten straling vrijkomen. De eerste soort wordt alfastraling genoemd. Hierbij breekt een helium-4-kern af van de kern van een atoom. Een heliumkern bevat twee protonen en twee neutronen:
|
… $$^4_2He \;\;\;\;\;\;\;\; (\alpha)$$ |
Hier zien we een voorbeeld van een vervalvergelijkingen waarbij α-straling vrijkomt. Het gaat hier om het verval van polonium-214:
$$^{214}_{84}\text{Po} \rightarrow ^{210}_{82}\text{Pb} + ^{4}_{2}\text{He}$$
Let op dat de som van de atoomnummers voor de reactie gelijk is aan de som van de atoomnummers na de reactie. Hetzelfde geldt voor de massagetallen. Het behoud van atoomnummer is een gevolg van het behoud van lading. Het behoud van massagetal is het gevolg van het behoud van massa. In het bovenstaande geval wordt door het verliezen van de heliumkern het nieuwe atoomnummer 82 en het nieuwe massagetal 210. In tabel 25 kan je zien dat bij deze waarden de stof Pb-210 hoort.
De tweede soort straling is bètastraling. Er zijn twee typen β-straling. De zogenaamde β+- en β--straling. Bij β--straling komt er een elektron uit de kern. Dit type straling wordt vaak ook gewoon β-straling genoemd. Bij β+-straling komt er een positron uit de kern. Een positron heeft dezelfde eigenschappen als het elektron alleen met een positieve lading. We noemen dit het antideeltje van het elektron.
|
…
|
Maar hoe kunnen er elektronen en positronen uit de kern komen? Het blijkt dat elektronen ontstaan als protonen of neutronen vervallen:
|
…
|
Hieronder zien we een voorbeeld van de twee typen β-straling:
$$^{40}_{19}\text{K} \;\rightarrow\; ^{40}_{20}\text{Ca} \;+\; ^{0}_{-1}\text{e}^-$$
$$^{22}_{11}\text{Na} \;\rightarrow\; ^{22}_{10}\text{Ne} \;+\; ^{0}_{1}\text{e}^+$$
In de eerste vergelijking is een neutron vervallen tot een proton en een elektron. Het atoomnummer is door het extra proton groter geworden. Het massagetal is gelijk gebleven, omdat in plaats van een neutron nu een proton in de kern zit. In de tweede vergelijking is het atoomnummer juist afgenomen. Dit gebeurt als een proton is vervallen in een neutron en een positron. Ook hier is het massagetal gelijk gebleven.
De laatste soort straling is gammastraling (γ-straling). Gammastraling bestaat uit fotonen (lichtdeeltjes) met een frequentie buiten het zichtbare spectrum. We schrijven:
|
… $$^0_0\gamma$$ … |
In BINAS tabel 25 kan je bij een aantal isotopen lezen welk type straling er wordt uitgezonden en met hoeveel (kinetische) energie de straling wordt weggeschoten.
Tot nu toe hebben we het gehad over reacties die spontaan plaatsvinden. We kunnen kernreacties echter ook kunstmatig opwekken. Een voorbeeld is het beschieten van een uraniumatoom met een neutron. Het neutron wordt ingevangen door de kern, waarna de kern in een aantal stukken uiteenvalt:
$$^{235}_{\;92}U \;+\; ^1_0n \;\rightarrow \;^{99}_{42}Mo \;+\; ^{134}_{\;50}Sn + 3^1_0n$$
Zoals je kunt zien komen bij deze reacties weer nieuwe neutronen vrij en deze neutronen kunnen weer tegen andere uraniumatomen botsen. De kans dat zo'n botsing plaatsvindt hangt o.a. af van de snelheid van deze neutronen. Te snelle neutronen zijn maar kort in de buurt van de volgende atoomkern en hebben daarom een kleinere kans om deze kern te doen splijten. In een kerncentrale wordt dit probleem opgelost met een moderator. Dit is een stof die ervoor zorgt dat neutronen afremmen. De juiste hoeveelheid hiervan kan een kettingreactie op gang brengen waarbij heel veel energie vrijkomt. Een gecontroleerde versie van zo'n kettingreactie vindt plaats in een kernreactor. Een ongecontroleerde versie vindt plaats bij het ontploffen van een kernbom.
Naast kernverval bestaat ook kernfusie. Hier fuseren atoomkernen samen. Ook bij dit proces kan energie vrijkomen. Dit gebeurt bijvoorbeeld in de zon. Hier wordt waterstof gefuseerd tot helium. De energie die hierbij vrij komt zorgt voor het licht dat de zon geeft.
|
|
|
1. Uit welke deeltjes bestaat α-, β+-, β-- en γ-straling.
2. Bij β--straling komt een elektron uit de kern van het atoom. Maar in de atoomkern zitten toch alleen protonen en neutronen? Leg uit hoe dit dan toch kan gebeuren.
3. Een α-deeltje verandert meestal in een heliumatoom. Wat moet er nog gebeuren om van een α-deeltje een heliumatoom te maken?
4. Wat is het verschil tussen een chemische reactie en een kernreactie?
5. Beschrijf de werking van een kettingreactie in een kerncentrale.
6. Beschrijf ook de functie van de moderator in een kerncentrale.
7. Medische artikelen zoals injectiespuiten mogen na gebruik niet meteen weggegooid worden, omdat ze verontreinigd kunnen zijn met schadelijke bacteriën. Daarom worden ze eerst gesteriliseerd met behulp van gammastraling. Een medewerker van het ziekenhuis is bang dat na de bestraling de bacteriën misschien wel dood zijn, maar dat de artikelen nu straling uitzenden. Leg uit of ze gelijk heeft.
|
|
|
|
8. Noteer de reactievergelijking van francium-221. Gebruik hiervoor de de laatste kolom in tabel 25.
9. Een ander atoom verandert onder uitzending van een α-deeltje in een radium-224-atoom. Wat was het oorspronkelijke deeltje waaruit dit isotoop van radium ontstaan is?
10. Noteer de vervalvergelijking van plutonium-240.
11. Noteer de vervalvergelijking van gallium-72.
12. Noteer de vervalvergelijking van barium-137.
13. Noteer de twee mogelijke reactievergelijkingen van Broom-80.
14. Noteer de vervalvergelijking tin-121-kern.
15. Uranium-233 vervalt o.a. doormiddel van K-vangst. Bij dit proces valt een elektron uit de eerste schil in de atoomkern. a. Geef de bijbehorende kernvervalvergelijking. b. Bij K-vangst gaat het elektron dat in de kern valt een reactie aan met een proton en samen vormen ze een neutron. Laat zien hoe je dit aan de vervalreactie bij vraag a kan zien.
16. De stof tritium (H-3) kan worden verkregen door lithium-6 te beschieten met een neutron. Bij deze stof komt naast tritium ook nog een ander deeltje vrij. Schrijf de bijbehorende kernreactievergelijking op.
17. Als splijtstof in een kernreactor wordt uranium-235 gebruikt. De kern hiervan splijt als er een neutron wordt ingevangen. Bij een bepaalde splijting ontstaan drie nieuwe neutronen en is barium-147 een van de splijtingsproducten. Geef de reactievergelijking van deze splijting.
18. De kernfusies die in de zon plaatsvinden, staan bekend onder de naam 'proton-proton-chain'. Hieronder zien we dit proces afgebeeld.
a. Bij de eerste reactie ontstaat waterstof-2 en een nog een ander deeltje. Leg uit om welk deeltje het hier gaat. b.
Bij de laatste reactie ontstaat een heliumkern en nog twee dezelfde
andere deeltjes. Leg uit om welke deeltjes het hier gaat.
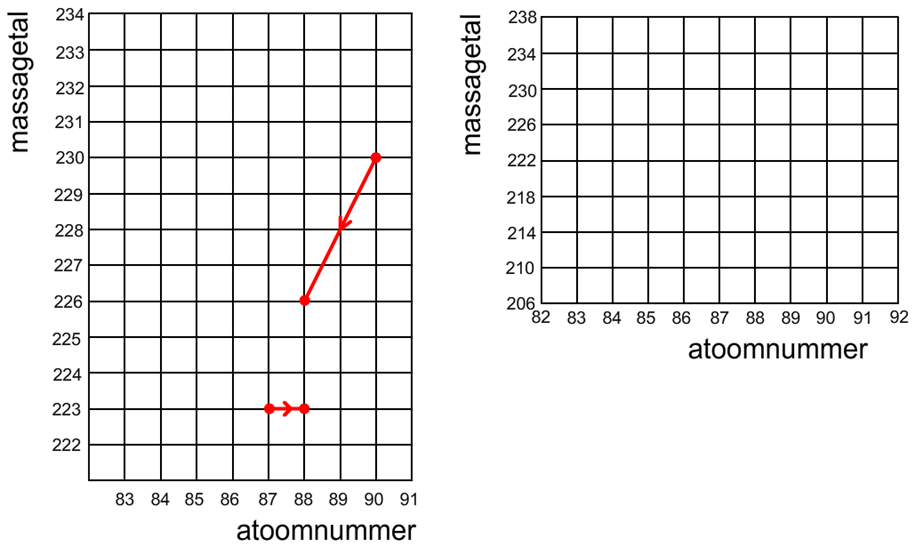
19. In het volgende linker diagram zijn twee vervalprocessen beschreven:
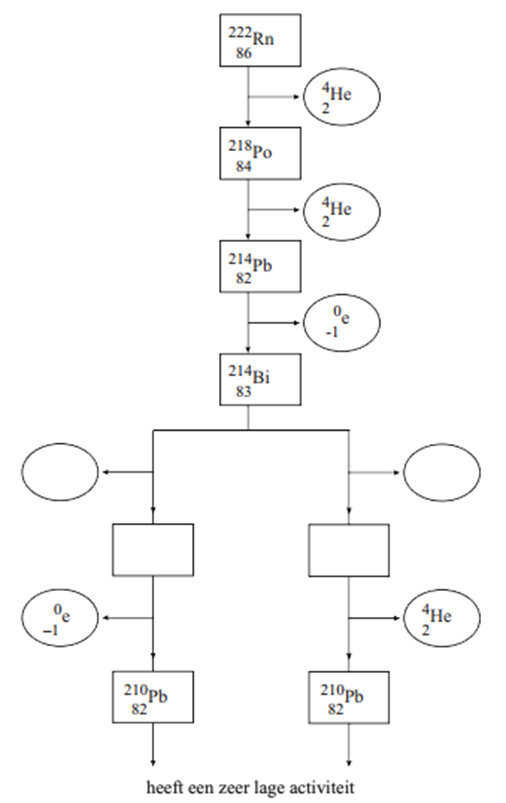
a. Leg uit welk type verval wordt weergegeven door nummer 1 en 2? b. Sommige isotopen vervallen niet één keer, maar meerdere keren. Bij deze isotopen blijft na het uitzenden van straling een dochterkern over die zelf ook weer instabiel is en straling uit zal zenden. We noemen deze ketting aan vervalreacties een vervalreeks. Teken in het rechter diagram de vervalreeks van uranium-238. De vervalreeks eindigt op het moment dat een stabiel element ontstaat. Laat Po-214 vervallen door middel van alfaverval en Bi-214 en Bi-210 door middel van bètaverval.
|
§3 Halveringstijd
In deze paragraaf gaan we bestuderen hoe het aantal radioactieve deeltjes in een bron afneemt in de tijd. We gebruiken hiervoor het begrip halveringstijd. Dit is de tijdsduur waarna de helft van de kernen vervallen is.
In de vorige paragraaf hebben we gezien dat radioactieve atoomkernen naar verloop van tijd straling uitzenden. Als dit gebeurt is, dan zeggen we dat het atoom vervallen is. De tijdsduur waarna de helft van het aantal deeltjes in de bron vervallen is, noemen we de halveringstijd of de halfwaardetijd (t1/2).
In het onderstaande (N,t)-diagram zien we het aantal radioactieve deeltjes in een bron (N) uitgezet tegen de tijd (t). In dit geval zien we dat het aantal radioactieve kerndeeltjes elke 10 uur halveert. Voor deze bron geldt dus een halveringstijd van 10 uur.
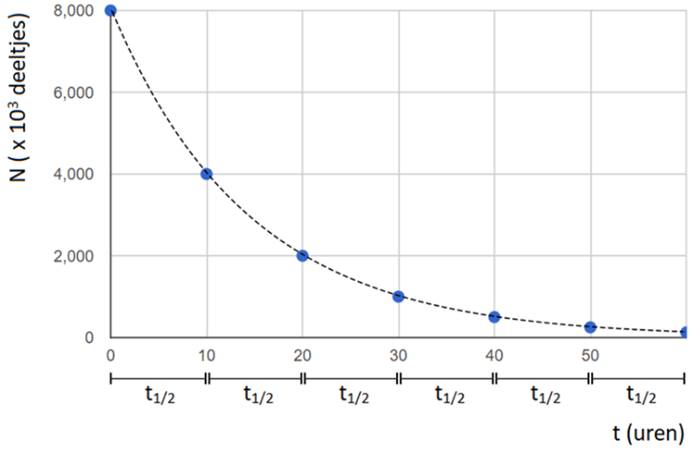
Elke radioactieve isotoop heeft zijn eigen halveringstijd en deze kan variëren van een fractie van een seconde tot miljoenen jaren. Voor een aantal isotopen is de halveringstijd te vinden in BINAS tabel 25. In deze tabel vinden we bijvoorbeeld dat Koolstof-14 een halveringstijd heeft van 5730 jaar. Na 5730 jaar is dus nog maar de helft van de koolstof-14 over. Na 2 × 5730 = 11 460 jaar is nog slechts 25% over en na 3 × 5730 = 17 190 jaar nog 12,5%. Etc.
Het aantal radioactieve deeltjes waaruit een bron bestaat op tijdstip t = 0 noemen we N0. Het aantal radioactieve deeltjes dat nog over is een tijdstip t later noemen we Nt. Als een stof in deze tijd bijvoorbeeld 3x gehalveerd is, dan geldt:
$$N_t = N_0 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} $$
Dit korten we af tot:
$$N_t = N_0 \left( \frac{1}{2} \right)^{3}$$
Een algemene formule voor het aantal radioactieve deeltjes op tijdstip t wordt dus:
|
… $$N_t = N_0 \left( \frac{1}{2} \right)^{n}$$
|
|
VWO |
||||||
|
|
||||||
|
… $$\frac{\log{(N_t/N_0)}}{ \log{(1/2) }} = n$$
|
||||||
|
|
Als we het aantal halveringen met de halveringstijd vermenigvuldigen, dan vinden we de tijd t die er voorbij is gegaan:
|
… $$t = n \times t_{1/2}$$
|
Je bent in deze formule voor de tijd en de halveringstijd niet gebonden aan de seconde.
Je kan beide tijdens dus ook best in bijvoorbeeld dagen of jaren invullen.
De formule wordt ook vaak herschreven tot:
|
… $$\frac{N_t}{N_0} = \left( \frac{1}{2} \right)^{n}$$ … |
De linkerkant van de vergelijking geeft nu de fractie van deeltjes dat
op tijdstip t nog over is. Als we de fractie met 100 vermenigvuldigen, dan
vinden we het percentage dat over is. Als op een bepaald moment geldt dat Nt/N0
= 0,09, dan weten we dat nog 9% van de kernen over is.
De halveringstijd van stoffen kan o.a. gebruikt worden voor radiometrische datering. Het bekendste voorbeeld hiervan is C14-datering. Koolstof-14 komt in vergelijk met andere koolstof isotopen in elk levend organisme in een vaste verhouding voor. Als een organisme echter sterft, krijgt het geen nieuwe koolstof-14 meer binnen en neemt deze hoeveelheid in de tijd af door kernverval. Door te kijken hoeveel koolstof-14 er nog over is, kunnen we met de halveringstijd uitrekenen hoe lang geleden het organisme gestorven is.
|
Voorbeeld |
|
$$m = 238,05 \text{ u}$$
De u is hier de zogenaamde atomaire massa-eenheid. Als we dit willen omschrijven naar kilogram, dan gebruiken (zie BINAS 7B):
$$1 \text{ u} = 1,6605 \times 10^{-27} \text{ kg}$$
Voor het uranium-238 isotoop vinden we dan:
$$238,05 \times 1,6605 \times 10^{-27} = 3,9528 \times 10^{-25} \text{ kg}$$
Als we nu het aantal deeltjes willen weten in 12 μg Uranium-238, dan delen we deze massa door de massa van één kern. We vinden:
$$\frac{12 \times 10^{-9}}{3,9528 \times 10^{-25}} = 3,0 \times 10^{16} \text{ kernen}$$
We hebben hier gebruikt dat:
$$12 \;\mu\text{g} = 12 \times 10^{-6} \text{ g} = 12 \times 10^{-9} \text{ kg}$$
|
|
|
|
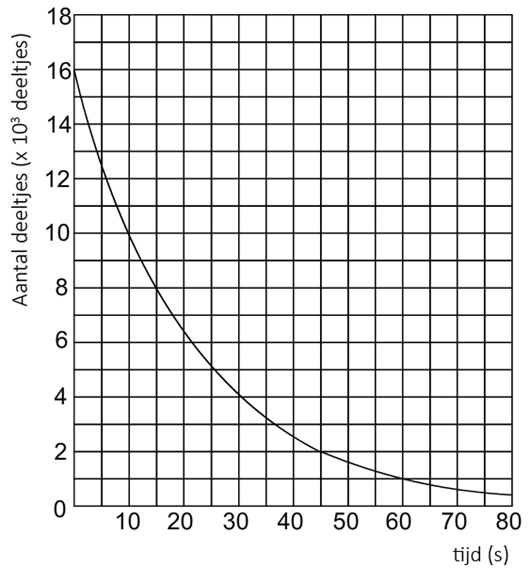
1. Hieronder zien we een diagram waarin het verval van technetium-100 wordt weergegeven.
a. Bepaal de halveringstijd van technetium-100 met behulp van de volgende grafiek. b. Stel dat je 2000 deeltjes technetium-100 hebt. Bepaal hoeveel deeltjes je nog over hebt na 1,0 minuut. c. (VWO) Stel dat je 1,0 kg technetium-100 hebt. Bepaal hoeveel gram je na 10 minuten nog over hebt.
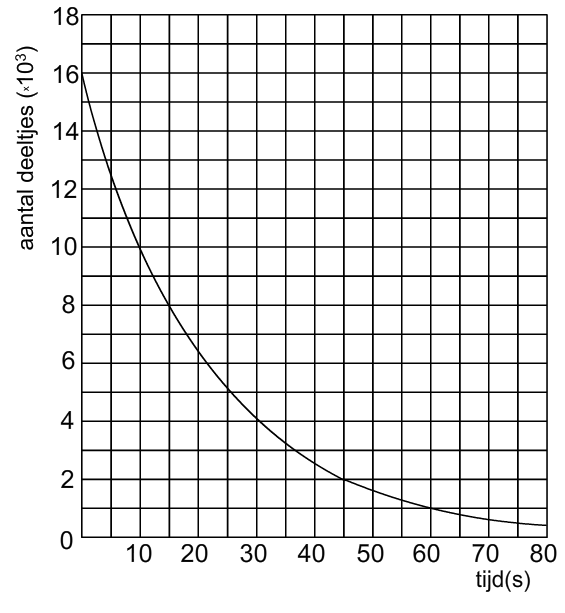
2.
In het volgende diagram wordt het
verval van een radioactieve stof beschreven. Maak het ontbrekende deel van de
grafiek af. 3. Het isotoop nikkel-63 vervalt door bètaverval in koper-63. Stel je hebt 1,60 gram nikkel-63. a. Bereken hoe lang duurt het voordat je nog slechts 0,0500 gram over hebt. b. Bereken hoeveel deeltjes er in deze tijd vervallen zijn. Zoek hiervoor eerst in tabel 25 de massa van het nikkel-63-isotoop op.
4. Het isotoop kalium-42 vervalt door bètaverval in calcium-42. Stel dat je in het begin 2,4 microgram hebt. a. Bereken hoe lang het duurt voordat je nog slechts 0,15 microgram over hebt. b. (VWO) Bereken hoe lang het duurt voordat je nog 0,025 microgram over hebt. c.
Bereken het aantal deeltjes kalium-42 die je aan het begin had en
gebruik dit voor het tekenen van een (N,t)-diagram. |
|
|
|
5. Leg uit in welke vorm de formule voor de halveringstijd geschreven moeten worden als je wil berekenen hoeveel procent van radioactief materiaal na een bepaalde tijd nog over is.
6. Een stukje tin bevat een kleine hoeveelheid tin-121. Deze isotoop vervalt onder uitzending van een bètadeeltje. Bereken hoeveel procent van het oorspronkelijke tin-121 er nog over is na 5 dagen.
7. Er worden restanten gevonden van een boom van 40.000 jaar oud. De koolstof-14 die ooit aanwezig was is voor een groot deel verdwenen. Hoeveel procent van de oorspronkelijke koolstof-14 zit er nu nog in de boom?
8. (HAVO) Een mummie wordt gevonden in een houten sarcofaag. De leeftijd van het hout wordt gevonden met behulp van koolstofdatering met behulp van het isotoop C-14. Uit een chemische analyse blijkt dat in de loop van de jaren 35% van C-14 vervallen is. Laat zien dat de mummie 3,6 x 103 jaar oud is.
9. (VWO) Een mummie wordt gevonden in een houten sarcofaag. De leeftijd van het hout wordt gevonden met behulp van koolstofdatering met behulp van het isotoop C-14. Uit een chemische analyse blijkt dat in de loop van de jaren 35% van C-14 vervallen is. Bereken hoeveel jaar voor Christus de mummie begraven is.
10. Een kerncentrale produceert een bepaalde hoeveelheid radioactief afval. De belangrijkste radioactieve stof in het afval is kobalt-60. Bereken hoe lang het duurt totdat slechts 1/250ste deel van de radioactieve stof over is gebleven.
|
§4 Activiteit
In deze paragraaf gaan we de activiteit van een radioactieve bron bestuderen. De activiteit is een maat voor de hoeveelheid kernen die per tijdseenheid vervalt.
Het aantal deeltjes dat in een bepaalde tijdseenheid vervalt noemen we de activiteit (A). De SI-eenheid van de activiteit is de Becquerel (Bq). Becquerel staat voor het aantal deeltjes dat per seconde vervalt. We kunnen de activiteit berekenen met de volgende formule:
|
… $$A = -\frac{\Delta N}{\Delta t}$$
|
De activiteit op een bepaald tijdstip kunnen we bepalen door een raaklijn te
tekenen in een (N,t)-diagram. Dit is hieronder gedaan. Omdat de raaklijn naar
beneden loopt vinden we een negatieve waarde. Door de extra min in de formule
wordt de activiteit toch positief.
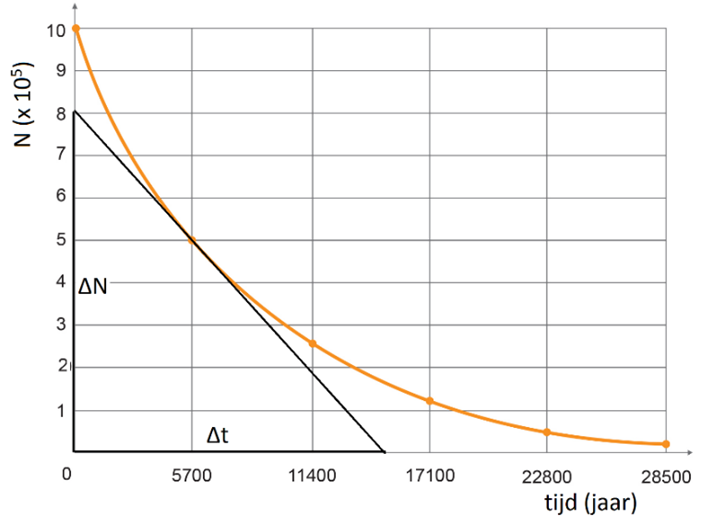
De activiteit neemt gedurende de tijd af volgens de volgende formule:
|
… $$A_t = A_0 \left( \frac{1}{2} \right)^{n}$$
|
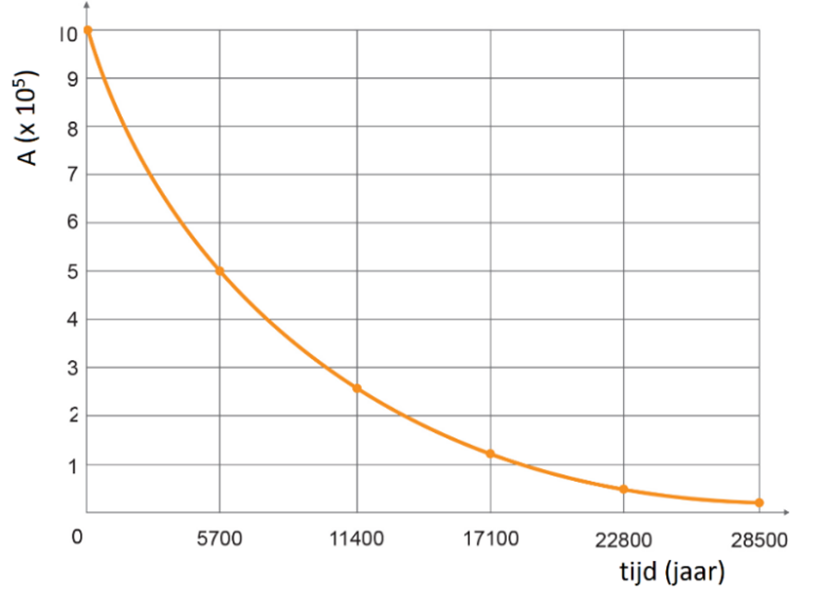
Ook bij deze formule hoort een grafiek (zie de onderstaande afbeelding). Merk op dat deze grafiek dezelfde vorm heeft als het (N,t)-diagram uit de vorige paragraaf. Het oppervlak onder een (A,t)-grafiek is gelijk aan het aantal deeltjes dat vervallen is (ΔN).
|
4 VWO |
||||||
|
|
||||||
|
… $$A = \frac{ln(2)}{t_{1/2}} N$$
|
||||||
|
Belangrijk is dat bij deze formule de tijd altijd in seconde gegeven moet worden.
|
|
|
|
1. Wat verstaan we onder de activiteit van een radioactieve bron?
2. Wat gebeurt er met de activiteit van een bron als je een halveringstijd wacht. Licht je antwoord toe.
3. Een radioactieve bron heeft een activiteit van 4,5 × 103 Bq en een grote halveringstijd. Bereken hoeveel atoomkernen vervallen in 10 minuten.
4. In een radioactieve bron vervallen in 1,0 minuut gemiddeld 3000 kernen. Bereken de gemiddelde activiteit van deze bron.
5. Hieronder zien we het (N,t)-diagram van het verval van technetium-100:
a. Bepaal de activiteit op tijdstip t = 0 s met behulp van een raaklijn. b. (VWO) Bepaal de activiteit op tijdstip t = 0 s met behulp van de formule A = N ln(2)/t1/2. Laat zien dat je op hetzelfde antwoord uitkomt. c. Bepaal de activiteit op tijdstip t = 30 s met behulp van een raaklijn. d. Bepaal de activiteit op tijdstip t = 30 s met behulp van At = A0(1/2)n. Gebruik hiervoor het antwoord van vraag a.
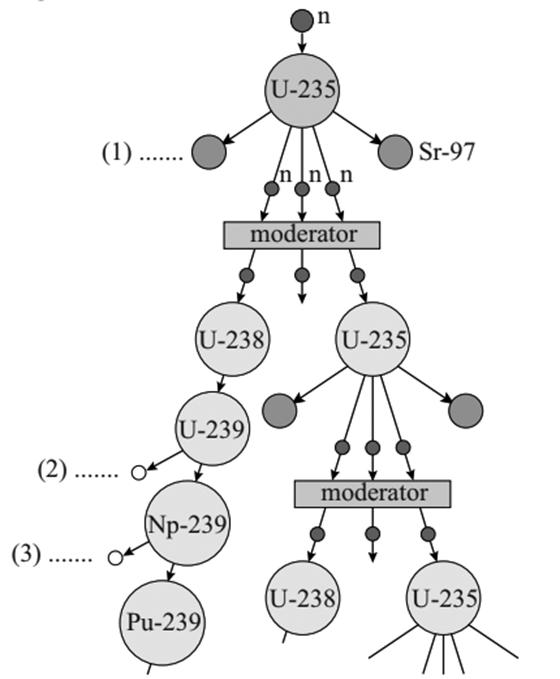
6. In het onderstaande figuur zien we het proces van kernsplijting weergegeven dat zich in een kerncentrale afspeelt.
a. Welke atoomkern of welk deeltje is ontstaan bij de (1), de (2) en de (3) in de afbeelding? b. Bij een moderne kerncentrale vervult het koelwater onder meer de functie van moderator. Leg uit wat een moderator doet. c. Aan de moderator wordt soms ook boorzuur toegevoegd. Dit heeft als gevolg dan een deel van de neutronen door boor-10-kernen ingevangen wordt. Bij deze reactie ontstaat tritium (H-3) en helium. Noteer de bijbehorende kernvervalvergelijking. d. Tritium is zelf ook weer radioactief. Op een gegeven moment zitten er 1,8 x 1022 deeltjes tritium in de moderator. Teken een (N,t)-diagram en bepaal hiermee de activiteit op tijdstip t = 0s. e.
(VWO) Beantwoord nu de vorige vraag met een berekening (dus zonder
grafiek).
7. Voor een onderzoek naar β--straling, heeft een leerling een radioactieve bron met P-32 laten maken. Hierbij is 1,0 gram P-32 gebruikt. Ten tijde van het onderzoek heeft de bron nog een activiteit van 2,5 x 1012 Bq. a. (VWO) Bereken de tijd tussen het maken van de bron en het onderzoek. b. (HAVO) Bereken hoeveel deeltjes er aan het begin in de radioactieve bron zitten. c.
(HAVO) Ten tijde van het maken van de bron heeft de stof een
activiteit van 1,6 × 1014 Bq. Bereken de tijd tussen het
maken van de bron en het onderzoek.
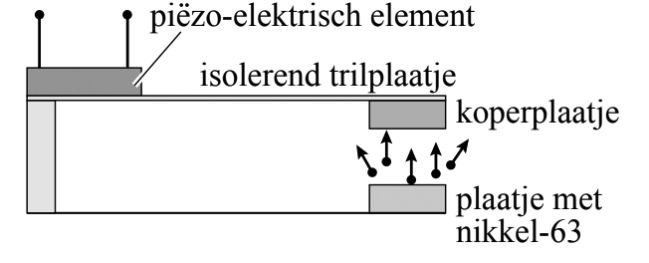
8. Nucleaire batterijen zijn spanningsbronnen die β--straling gebruiken om elektrische energie op te wekken. Door hun zeer kleine afmetingen zijn ze bijzonder geschikt voor microprocessoren in computers en in pacemakers. De β--straling komt uit een radioactieve bron die bestaat uit een plaatje met nikkel-63. a. Geef de reactievergelijking voor het verval van nikkel-63. b.
Het principe van een nucleaire batterij wordt toegelicht met behulp
van de onderstaande afbeelding. Een aantal β--deeltjes uit
het plaatje met nikkel-63 treft een koperplaatje en wordt daar geabsorbeerd.
Het koperplaatje is bevestigd aan een isolerend trilplaatje dat goed kan
buigen. Aan het isolerend trilplaatje is ook een piëzo-elektrisch element
bevestigd. Dit element geeft bij vervorming een elektrische spanning af. c. Op een gegeven moment zitten er 2,27 × 1020 deeltjes nikkel-63 in het plaatje. Bereken de massa van het nikkel-63 in het plaatje, uitgedrukt in kg. d. (VWO) De activiteit van het nikkel-63 in het plaatje is op een gegeven moment 5,0 x 1010 Bq. Bereken de massa van het nikkel-63 in het plaatje, uitgedrukt in kg. e.
Bij het verval van een nikkel-63-kern komt per vervalreactie 62 keV
aan kernenergie vrij. Het rendement van de omzetting van kernenergie naar
elektrische energie is bij dit proces 4,0%. f.
(VWO) Een nucleaire batterij is toegepast in een pacemaker. Zolang
het vermogen van de nucleaire batterij meer dan 90% is van het vermogen bij
de productie, kan hij worden gebruikt. Het rendement blijft bij het
teruglopen van het vermogen gelijk. Bereken hoe lang na de productie de
nucleaire batterij vervangen moet worden.
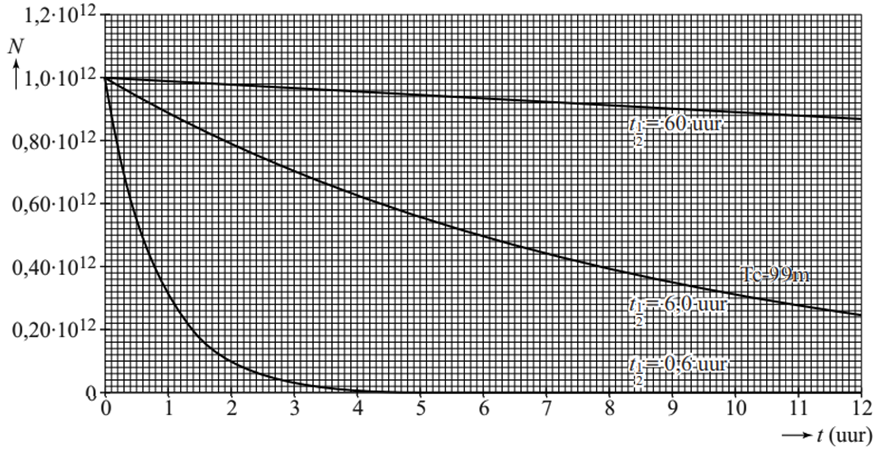
9. In Petten staat een kerncentrale waar isotopen voor medische toepassingen worden geproduceerd. Eén van de belangrijkste producten is molybdeen-99 (Mo-99). Mo-99 wordt naar ziekenhuizen getransporteerd. Ondertussen vervalt een deel tot technetium-99m, dat gebruikt wordt voor medische behandelingen. Iedere keer als men Tc-99m nodig heeft voor een behandeling, wordt dit afgescheiden van het molybdeen. In ziekenhuizen wordt wekelijks een nieuwe voorraad Mo-99 aangevoerd. a. Bereken hoeveel procent van de oorspronkelijke hoeveelheid Mo-99 er na een week nog over? b. Tc-99m is metastabiel. Dit betekent dat de protonen en neutronen in de kern van een Tc-99m atoom zich kunnen herschikken tot een toestand met een lagere energie. Bij het verval van Tc-99m naar Tc-99 komt een foton vrij. Door deze fotonen is Tc-99m geschikt als tracer. Een tracer is een radioactieve stof die in het lichaam gebruikt kan worden om bijvoorbeeld de locatie van tumoren te achterhalen. Een voorwaarde voor een radioactieve tracer is dat de totale activiteit voor de patiënt zo laag mogelijk blijft. Een arts kan voor een behandeling kiezen uit tracers met verschillende halveringstijden (zie de onderstaande afbeelding). Voor Tc-99m geldt een halveringstijd van 6,0 uur.
c.
Leg met behulp van de afbeelding uit waarom er meer tracer toegediend
moet worden bij stoffen met halveringstijden van 60 uur en 0,6 uur om tot
dezelfde activiteit te komen 3,0 uur na het toedienen.
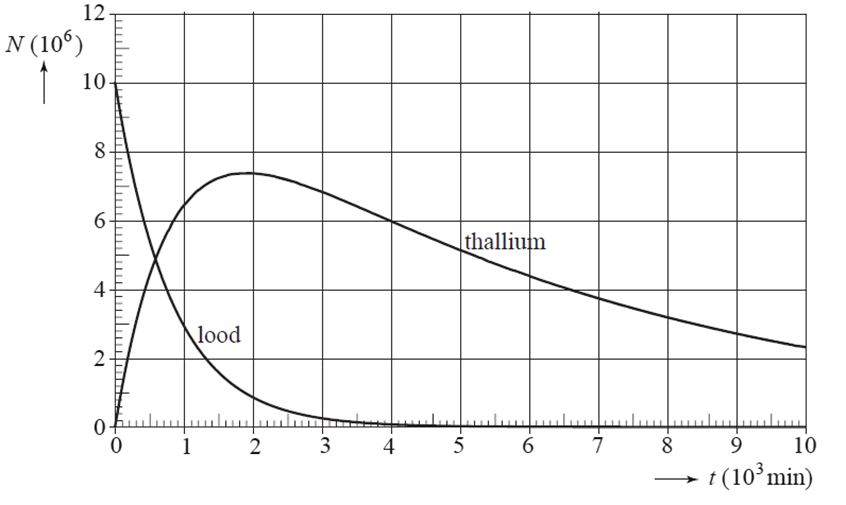
10.
(VWO) De isotoop Pb-201
wordt gebruikt in de nucleaire geneeskunde, onder andere bij de diagnose van
problemen aan het hart. Pb-201 vervalt tot Tl-201. Het Tl-201 vervalt verder,
waarbij het onder andere γ-straling uitzendt. Op het tijdstip t = 0 s
zijn er alleen kernen van Pb-201. In de onderstaande afbeelding staat het
aantal kernen Pb-201 en Tl-201 als functie van de tijd. a. Op een bepaald moment is de activiteit van het Tl-201 maximaal. Zoals je in het bovenstaande diagram kan zien loopt de grafiek hier even horizontaal. Verklaar waarom dit het geval is. b.
Bepaal met behulp van de afbeelding de grootte van de activiteit van
het Tl-201 op dat moment.
|
§5 Stralingsgevaar
In deze paragraaf bestuderen we de gevaren van straling voor de mens. Ook bespreken we twee meetinstrumenten waarmee we straling kunnen meten.
Als radioactieve straling met genoeg kinetische energie een atoomkern verlaat, dan kan het andere atomen ioniseren (dit betekent dat één of meerdere elektronen uit de atomen getrokken worden). Alfastraling kan door zijn grotere massa en lading gemakkelijker ioniseren dan bètastraling. We zeggen dan ook dat alfastraling een groter ioniserend vermogen heeft. Ioniserende straling kan schadelijk zijn voor de gezondheid. Het kan bijvoorbeeld het DNA beschadigen en dit kan het begin zijn van een tumor. Het is dus belangrijk dat we in omgang met radioactieve bronnen goede voorzorgsmaatregelen treffen.
Er zijn twee manieren waarop je schade kan ondervinden van straling. De eerste is bestraling. Bij bestraling bevindt de radioactieve bron zich buiten het lichaam en ondervindt het lichaam schade door de straling die uit deze bron schiet. Als deze deeltjes echter hun impact gemaakt hebben, dan zijn ze verder onschadelijk. Als je dus van de bron wegloopt, dan neemt de schade niet toe. De straling zelf is immer niet radioactief. Bij besmetting komt de radioactieve bron in het lichaam terecht. Het is dus niet mogelijk om van deze bron weg te lopen. Besmetting is daarom over het algemeen gevaarlijker dan bestraling.
De schadelijke gevolgen van straling zijn afhankelijk van de energie van de straling en de massa van het lichaamsdeel dat de straling ontvangt. In formuletaal schrijven we dit als volgt op:
|
… $$D = \frac{E_{straling}}{m}$$ …
|
De totale stralingsenergie is gelijk aan de energie van één deeltje maal de
hoeveelheid vervallen deeltjes:
|
… $$E_{straling} = \Delta N \times E_{deeltje}$$
|
Het stralingsenergie per deeltje is voor veel isotopen te vinden in BINAS tabel
25. De eenheid die in deze tabel gebruikt wordt voor de energie is de
elektronvolt (eV):
$$1 \text{ eV} = 1,6 \times 10^{-19} \text{ J}$$
Ook wordt vaak Mev (mega-elektronvolt) gebruikt. Hier geldt:
$$1 \text{ MeV} = 1,6 \times 10^6 \times 10^{-19} \text{ J} = 1,6 \times 10^{-13} \text{ J}$$
Naast het verschil in energie heeft alfastraling ook een groter ioniserend vermogen. Alfastraling is daardoor 20x schadelijker dan bèta- en gammastraling. De totale impact van de schade van bestraling is gevat in het begrip equivalente dosis (H). De eenheid hiervan is sievert (Sv). De formule is:
|
… $$H = w_R D$$
|
wR is de zogenaamde stralingsweegfactor. Deze factor is gelijk aan 1 voor gamma- en bètastraling en gelijk aan 20 voor alfastraling.
Voor de veiligheid zijn er stralingsbeschermingsnormen opgesteld. Dit is de maximale effectieve dosis in millisievert per jaar die is toegestaan. Deze normen zijn te vinden in BINAS.
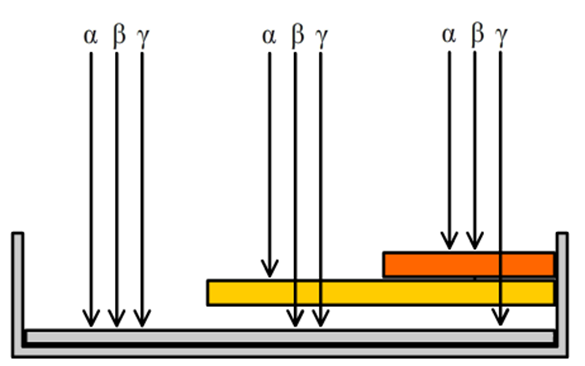
Om na te gaan hoeveel straling iemand binnenkrijgt, zijn een aantal meetinstrumenten ontworpen. De eerste die we bespreken wordt een badge genoemd. Dit is een klein meetinstrument dat mensen opgespeld krijgen op plekken waar met radioactief materiaal gewerkt wordt. Een badge maakt gebruik van het feit dat elk type straling een ander doordringend vermogen heeft. Alfastraling dringt niet ver in stoffen door. Zelfs door lucht kan alfastraling slechts enkele centimeters bewegen. Bètastraling dringt beter door en gammastraling het best. De afstand die deeltjes kunnen afleggen wordt de dracht genoemd. In de volgende afbeelding zien we een doorsnede van de badge. Het linker deel van de badge laat alle soorten straling door. Het middelste deel laat bèta- en gammastraling door en het rechter deel alleen gammastraling. De straling die doorgelaten wordt komt dan tegen een film aan die verkleurt afhankelijk van de hoeveelheid straling. Door de verkleuring op de drie plekken te vergelijken kan je van elk type straling achterhalen aan hoeveel straling de badge (en dus de persoon) heeft blootgestaan.
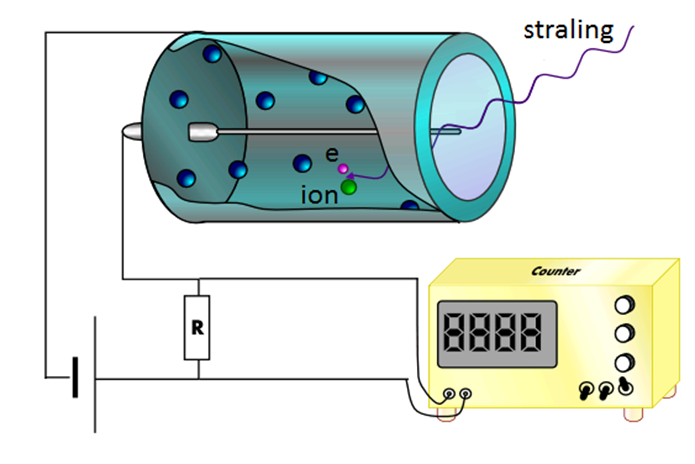
Een andere manier om ioniserende straling te meten is met een zogenaamde Geigerteller (GM-teller). Dit apparaat bestaat uit een buis met daarin een gas. Als ioniserende straling het gas binnenkomt, dan worden een aantal atomen van het gas geïoniseerd. De vrijgemaakte elektronen zorgen dan voor een kleine stroom en deze stroom zorgt in een luidspreker voor een hoorbaar piepje. Hoe meer piepjes je hoort, hoe meer straling er in de buurt is.
|
|
||||||||
|
1. Wat wordt er bedoeld met het ioniserend vermogen van straling.
2. Leg uit hoe je met een badge van elk type straling de hoeveelheid bestraling kan meten. Gebruik in je antwoord het begrip doordringend vermogen.
3. Leg uit hoe een geigerteller werkt.
4. Wat is het verschil tussen besmetting of bestraling.
5. Schrijf op hoe je elektronvolt (eV) en mega-elektronvolt (MeV) kan omrekenen naar joule (J).
|
||||||||
|
|
||||||||
|
6. Zoek in BINAS de stralingsbeschermingsnorm op voor een persoon werkende met radioactief materiaal en voor een individueel lid van de bevolking. In welke eenheid staat de norm gegeven?
7. Een werknemer heeft in een jaar 600 uur in een opslaghal gewerkt waar met radioactief materiaal wordt gewerkt. Daarbij heeft zijn gehele lichaam een gemiddeld dosis van 7,5 × 10-7 Gy per uur aan alfastraling ontvangen. Ga na of voor deze werknemer de stralingsbeschermingsnorm is overschreden.
8. Een persoon met een massa van 85 kg werkt in een kerncentrale waarin zijn hele lichaam is blootgesteld aan straling afkomstig van U-235. Hoeveel deeltjes mag deze werknemer per jaar ontvangen voordat de stralingsnormen overschreden worden.
9. In sommige granaten is wat uranium aanwezig. Deze stof wordt gebruikt vanwege zijn hoge dichtheid. Als een granaat op het slagveld ontploft, zal het aanwezige uranium verpulveren of verdampen en als stof of damp in de lucht aanwezig zijn. Veronderstel dat een soldaat een stofdeeltje inademt dat U-236 bevat. Dit stofdeeltje nestelt zich in een longblaasje. a. Leg uit dat de activiteit van het U-236 tijdens een mensenleven nauwelijks afneemt. b.
Een stofdeeltje dat door een soldaat wordt ingeademd heeft een
activiteit van 2,2 × 10-6 Bq. Bij het verval van één
uraniumkern komt een energie van 6,7 × 10-13 J vrij. Deze
vrijkomende energie wordt in 0,18 × 10-9 kg omringend weefsel
geabsorbeerd. Bereken de equivalente dosis die het bestraalde weefsel in
een jaar ontvangt.
10. Bij een bepaalde behandeling moet een stukje weefsel van 4,0 gram een stralingsdosis van 2 Gy ontvangen afkomstig van een iridiumpreparaat. De behandeling duurt 3,5 uur. De gemiddelde energie van de hierbij uitgezonden β-deeltjes is 0,6 MeV. Neem aan dat alle uitgezonden straling door het stukje weefsel wordt opgenomen. a. Bereken de gemiddelde activiteit die het ingebrachte iridium moet hebben. b.
(VWO) De activiteit van het iridium-192 daalt in de loop van de tijd.
Met hetzelfde iridiumpreparaat wordt de behandeling precies vier weken later
herhaald. Men wil dan dezelfde stralingsdosis toedienen aan hetzelfde stukje
weefsel. Bereken hoe lang de behandeling dan moet duren.
11. In een mijn is radon-222 aanwezig. De activiteit van het Rn-222 in de mijn bedraagt 65 Bq per liter lucht. De α-straling wordt vooral door het longweefsel geabsorbeerd. In de longen van een bepaalde persoon bevindt zich (gemiddeld) 6,0 liter lucht. Als gevolg van het verval van één Rn-222-kern absorbeert het longweefsel 3,1 x 10-12J stralingsenergie. Per uur absorbeert het longweefsel hierdoor 4,4 x 10-6J stralingsenergie. a. Toon met een berekening aan dat het longweefsel per uur de genoemde hoeveelheid stralingsenergie absorbeert. b.
Iemand verblijft tijdens zijn therapie 32 uur in de mijn. De massa
van zijn longen is 9,5 x 102 g.
12. Per splijting van een uranium-235-kern in een kerncentrale komt gemiddeld een hoeveelheid energie vrij van 190 MeV. Deze energie wordt met een rendement van 35% omgezet in elektrische energie. In één jaar vinden 2,93 x 1027 splijtingen in de kerncentrale plaats. Bereken het gemiddeld elektrisch vermogen in gigawatt dat de kerncentrale levert in dat jaar.
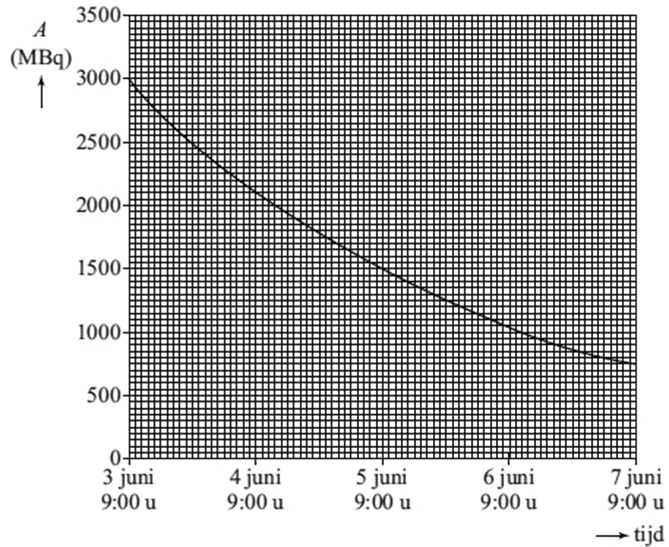
13. Cassie, een acht jaar oude hond met een tumor in een bot, is onlangs als eerste hond ter wereld succesvol behandeld met samarium-153. a. Samarium-153 komt niet in de vrije natuur voor. Het wordt gemaakt door samarium-152-kernen te beschieten met een bepaald soort deeltjes. Leg uit met welk deeltje een samarium-152-kern beschoten moet worden om samarium-153 te vormen? b. Samarium-153 zendt zowel β--straling als γ-straling uit. Het kan daarom zowel voor een behandeling tegen tumoren gebruikt worden als voor een scan. Geef de vervalreactie van samarium-153. c. Samarium hecht zich beter aan geïnfecteerd botweefsel dan aan gezond botweefsel. Daarom kan er tijdens de behandeling ook een scan gemaakt worden van de hond waarin zieke botdelen als lichte vlekken te zien zijn (zie de onderstaande foto). Welk soort straling wordt gebruikt om een scan te maken en van welke eigenschap van die straling wordt dan gebruikgemaakt? - β--straling, want deze straling heeft een klein doordringend vermogen - β--straling, want deze straling heeft een groot doordringend vermogen - γ-straling, want deze straling heeft een klein doordringend vermogen - γ-straling, want deze straling heeft een groot doordringend vermogen d. Het medicijn, met productiedatum 3 juni 9.00 uur, wordt aangeleverd in een flesje met een inhoud van 15 mL. De activiteit van het geleverde samarium-153 is hieronder weergegeven:
e.
Cassie is op 4 juni om 9.00 uur 's ochtends ingespoten met het medicijn.
Volgens de arts moet er 37 MBq per kg lichaamsgewicht geïnjecteerd worden.
Cassie heeft een massa van 30 kg. f.
De tumor in het bot van Cassie werd bestraald met de β--deeltjes
die door het samarium-153 zijn uitgezonden. Elk deeltje had een energie van
233 keV. Tijdens de behandeling heeft het geïnfecteerde bot een
stralingsdosis ontvangen van 86,5 Gy ten gevolge van de β--deeltjes. De
massa van het geïnfecteerde bot is 10 g. g.
Een deel van het bij Cassie ingespoten samarium is uitgescheiden met
de urine. De urine van Cassie werd daarom opgevangen en gedurende 10
halveringstijden bewaard. Bereken hoeveel procent van de activiteit van
het samarium in de opgevangen urine er na die tijd nog over was.
14. In de eerste helft van de vorige eeuw was het gebruikelijk om bij sommige aandoeningen een behandeling met radioactief radium-226 te ondergaan. Een patiënt moest dan een warm bad nemen waarin radiumzout aan het badwater was toegevoegd. Volgens sommige artsen uit die tijd kon de straling die bij het verval van radium vrijkwam door de huid van de patiënt heen gaan. a. Leg met behulp van de vervalreactie van radium-226 uit of die artsen gelijk hadden. b. Leg uit waarom het nemen van zo'n bad geen goed idee is. c. (HAVO) Op een bepaald moment bevat het badzout 1,16 × 1016 deeltjes. Bereken hoeveel microgram radium-226 dit potje badzout bevatte. d. (VWO) De activiteit van het radium-226 in het badzout was 1,6 x 105 Bq. Bereken hoeveel microgram radium-226 dit potje badzout bevatte. e.
Over het bad was een zeil gespannen, waar een buis doorheen stak. Via
de buis kon het radongas, dat bij het verval van het radium was ontstaan,
worden ingeademd. Het radongas vervalt in de longen en de
vervalproducten komen zo in het bloed en bij de organen terecht. In het
onderstaande figuur is een deel van de vervalreeks van radon-222 gegeven. In
deze reeks ontbreken twee vervalreacties. Vul het diagram aan. f. Vanuit het radium ontstaan 1,6 x 105 radonatomen per seconde. De activiteit hiervan is constant, tijdens het nemen van een bad. Er komt 25% van het radongas in het lichaam terecht. De energie van het α-verval van radon wordt, samen met de energie van het verval van alle dochterkernen, geabsorbeerd door het lichaam. Per ingeademd radondeeltje komt er 24,7 MeV aan energie vrij door α-verval. Veronderstel dat iemand van 80 kg gedurende 45 minuten in zo'n radiumbad zit. Bereken hoe vaak deze persoon maximaal jaarlijks zo'n bad zou kunnen nemen zonder dat de jaarlijkse effectieve totale lichaamsdosis wordt overschreden. g.
Bij plaatselijke klachten was het ook mogelijk om een kompres met
radium-226 op de pijnlijke plek te leggen. In 2006 werd een container
onderschept waarin een radiumkompres uit 1951 zat. Bij de productie in 1951
had dit kompres een activiteit van 7,4 MBq. Leg uit of de activiteit van
het radium in dit kompres in 2006 veel groter, bijna even groot of veel
kleiner was dan 7,4 MBq.
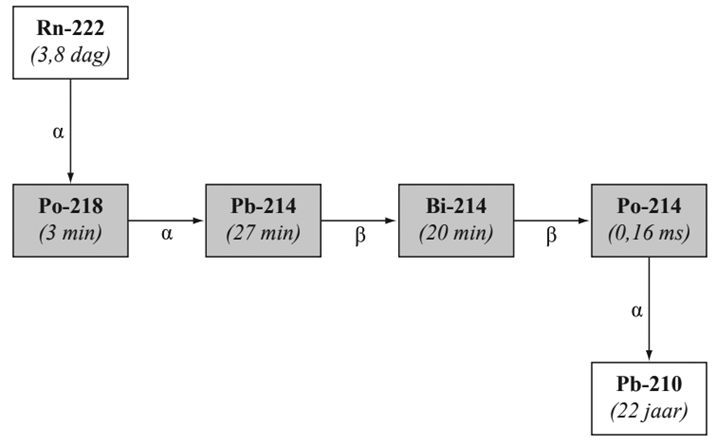
15. (VWO) Radon is een radioactief edelgas dat uit de bodem en uit bouwmaterialen kan ontsnappen en terecht kan komen in kelders en kruipruimtes die slecht geventileerd worden. De meest voorkomende isotoop van radon is radon-222. Radioactieve isotopen met atoomnummers tussen 82 en 90 komen in de natuur voor omdat ze voortdurend aangemaakt worden. Er bestaan in de natuur twee zogenoemde 'radioactieve reeksen'. De ene reeks begint bij thorium-232, de andere bij uraan-238. a. Beredeneer of radon-222 ontstaat uit thorium-232 of uit uraan-238. Beschouw daartoe het aantal nucleonen van de kernen. Hint: het is niet nodig om de vervalvergelijkingen op te schrijven. b.
In de volgende afbeelding zijn het verval van radon-222 en de daarop
volgende vervalstappen weergegeven. Bij elke isotoop is de halfwaardetijd
gegeven. c. Leg uit dat elk van de radondochters dan dezelfde activiteit heeft als radon-222. d.
Een persoon die een tijdje in zo'n kelderruimte verblijft, ademt
lucht in met de daarin aanwezige isotopen. Stel dat een persoon tijdens zijn
verblijf in de kelderruimte 1 m3 lucht inademt. De persoon
ademt het radon weer uit omdat het een edelgas is. De microscopische
stofdeeltjes met de radondochters blijven achter in de longen. Bij het verval
hiervan worden de longen (totale massa van 2,5 kg) bestraald. In de
onderstaande tabel staat het aantal kernen in 1 m3 lucht van
elk van de radondochters in de kelderruimte:
Bereken
de stralingsdosis die de longen ontvangen ten gevolge van alfastraling.
|
§6 Medische beeldvorming
Radioactieve stoffen worden o.a. gebruikt in ziekenhuizen bij het maken van scans van de binnenkant van het menselijk lichaam. Denk bijvoorbeeld aan de PET-scan. In de paragrafen bespreken we ook een aantal andere typen scans, waaronder de MRI-scan, de röntgenscan en de echo.
Kennis van atoomkernen wordt in de medische wetenschap veel toegepast. Een veelvoorkomende techniek is dat chemische verbindingen ingespoten worden in het lichaam waarbij één of meerdere atomen zijn vervangen door een radioactieve isotoop. We noemen een dergelijke stof een tracer. Deze stoffen hopen zich in bepaalde plekken van het lichaam op en zenden daar gammastraling uit. Een deel van deze straling zal het lichaam verlaten en kan gedetecteerd worden. We noemen deze techniek scintigrafie.
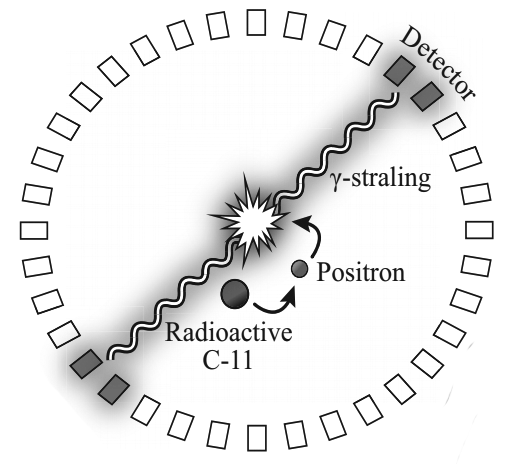
Een belangrijk voorbeeld hiervan is de PET-scan. De tracer zendt in dit geval positronen uit. Als een positron tegen een elektron in het lichaam botst, dan worden beide deeltjes geheel omgezet in twee fotonen die in tegengestelde richting wegschieten. We noemen dit annihilatie:
$$e^- + e^+ \;\;\;\rightarrow\;\;\; \gamma + \gamma$$
Omdat fotonen een grotere dracht hebben, zal een groot aantal hiervan het lichaam verlaten. Deze fotonen worden dan gedetecteerd door een cirkelvormige detector, zoals hieronder is weergegeven. Door het verschil in tijd te meten tussen de aankomst van beide fotonen, kan met Δx = cΔt de positie van de annihilatie bepaald worden.
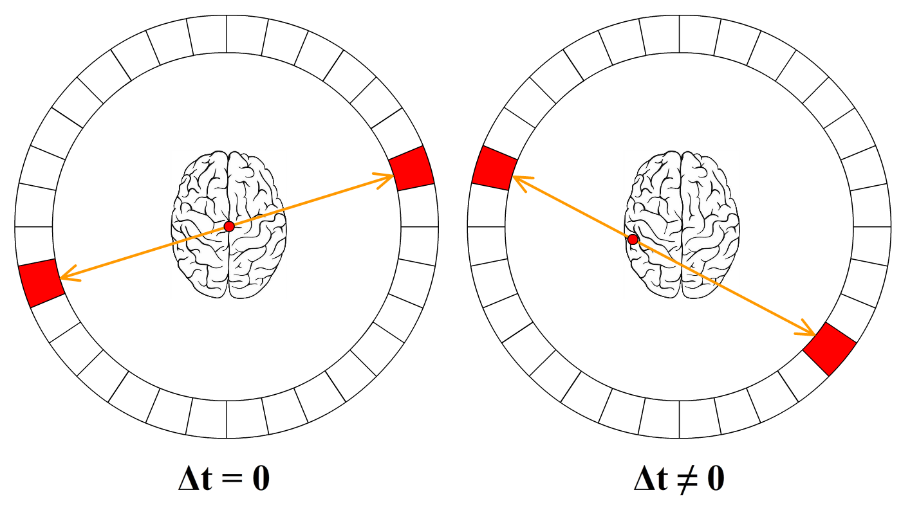
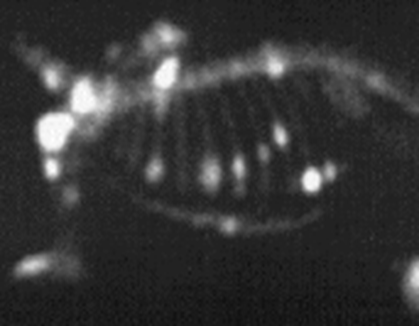
Hieronder zien we een voorbeeld van een PET-scan van de hersenen. Er is in dit geval als tracer glucose gebruikt met daarin een radioactief isotoop. Hersendelen die meer actief zijn nemen meer glucose op en als gevolg lichten deze delen meer op in de PET-scan. Op deze manier kunnen we dus een idee krijgen van hersenactiviteit.
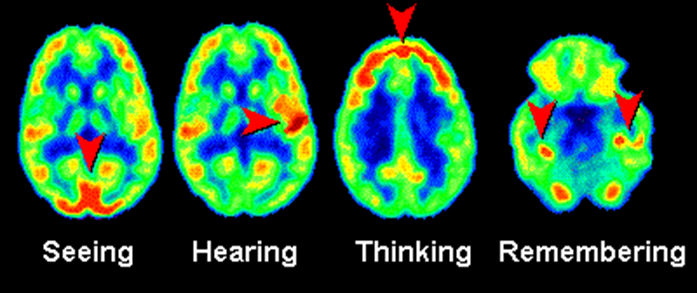
Deze methode kan ook gebruikt worden bij het lokaliseren van tumoren. Een bekend voorbeeld is het gebruik van een jood-tracer voor het onderzoek naar de schildklier. De schildklier neemt relatief veel jood op als gevolg is deze goed zichtbaar met een PET-scan.
VWO |
|
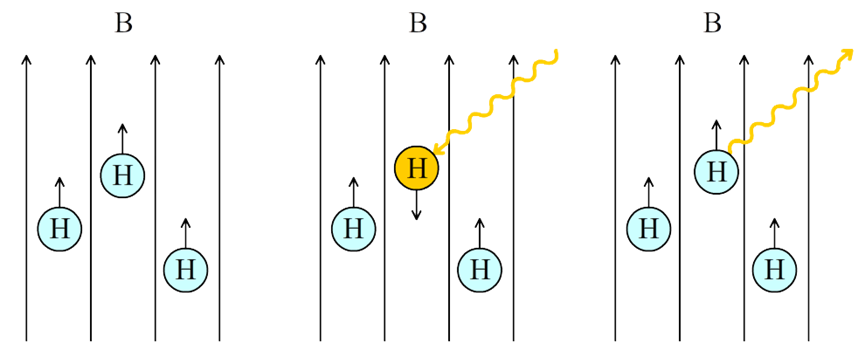
Na een korte tijd zal het waterstofatoom weer terugvallen naar zijn grondtoestand en hierbij wordt hetzelfde foton weer uitgezonden (zie de rechter afbeelding). Een deel van deze fotonen wordt buiten het lichaam gedetecteerd en hiermee wordt de foto gemaakt.
Waterstof atomen komen o.a. voor in water. Hoe meer water dus in een deel van het lichaam zit, hoe meer fotonen hier dus vandaan zullen komen. Met behulp van verschillen in de waterstofdichtheid kan het lichaam hiermee nauwkeurig in kaart worden gebracht (zie de onderstaande afbeelding).
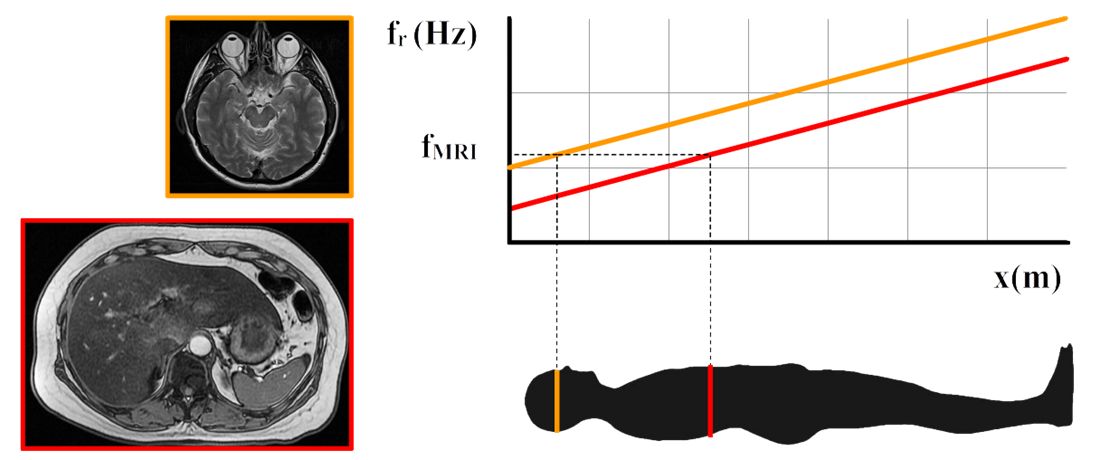
Om een foto te maken willen we echter alleen fotonen ontvangen van een twee-dimensionale 'slice' van het menselijk lichaam. Dit wordt gedaan door de sterkte van het magneetveld te variëren langs het menselijk lichaam. Als gevolg krijgt elk deel van het menselijk lichaam ook zijn eigen resonantiefrequentie. Waterstofatomen zullen nu alleen aangeslagen worden op de plek waar de frequentie van de gebruikte fotonen (fMRI) gelijk is aan de resonantiefrequentie (fr). Door het magneetveld te versterken of verzwakken, kunnen we op deze manier verschillende delen van het lichaam in kaart brengen (zie de onderstaande afbeelding).
|
Bij echoscopie wordt gebruik gemaakt van geluidsgolven om het menselijk lichaam in kaart te brengen. Hieronder zien we bijvoorbeeld een echo van een foetus. Deze foto is gemaakt door korte geluidspulsen de buik van een zwangere vrouw in te sturen. Een deel van deze geluidsgolven reflecteert op het moment dat ze van het ene naar het andere type weefsel overgaan. Doordat de golven vaak door meerdere lagen weefsel trekken, krijg je ook meerdere pulsen terug. Door te meten hoe lang het duurt voordat de verschillende pulsen terugkomen, kan een beeld gemaakt worden van de foetus. Door ook te meten hoeveel van de golf gereflecteerd is, kan ook iets worden gezegd over het type stof waartegen de geluidgolven reflecteren.
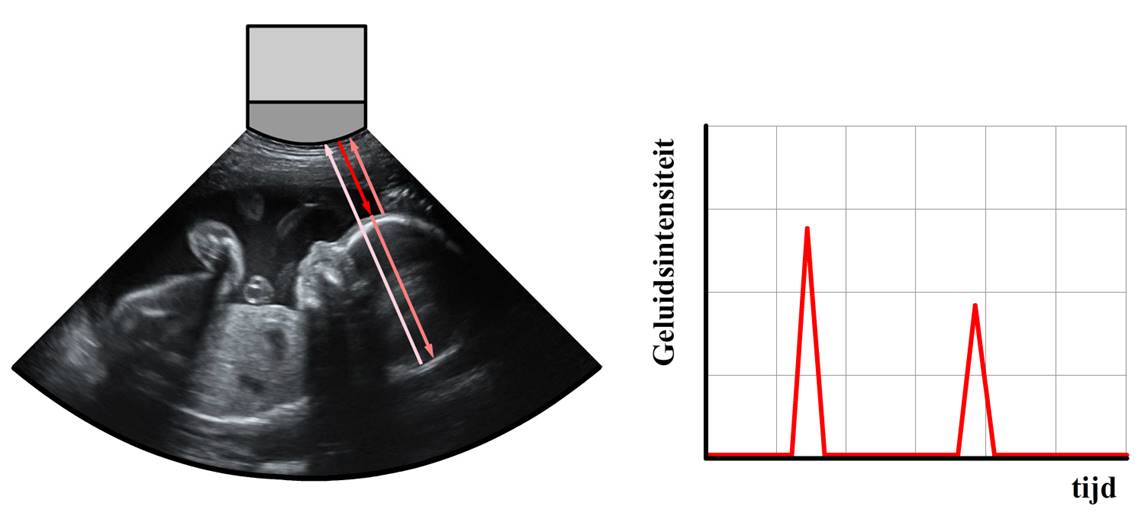
Voor het maken van een echo kan geen geluid gebruikt worden dat met het menselijk oor hoorbaar is. Dit gelijk heeft namelijk een golflengte die veel groter is dan de details die we met een echo willen zien. In het hoofdstuk kwantum hebben we gezien dat golven in dat geval om het voorwerp heen zullen buigen en er dus geen scherp beeld meer gemaakt kan worden. Een geluidsgolf van bijvoorbeeld 5,0 MHz kan wel gebruikt worden. Bij een temperatuur van ongeveer 40 graden Celsius is de geluidsnelheid in water gelijk aan 1,5 × 103 m/s. De bijbehorende golflengte is dan:
$$\lambda = \frac{v}{f}$$
$$\lambda = \frac{1,5 \times 10^3}{5,0 \times 10^6} = 0,30 \text{ mm}$$
Dit wil zeggen dat we met deze frequentie details kunnen waarnemen van zo'n 0,30 mm. Dit levert het 'pixel-achtige' beeld op dat in de bovenstaande afbeelding te zien is.
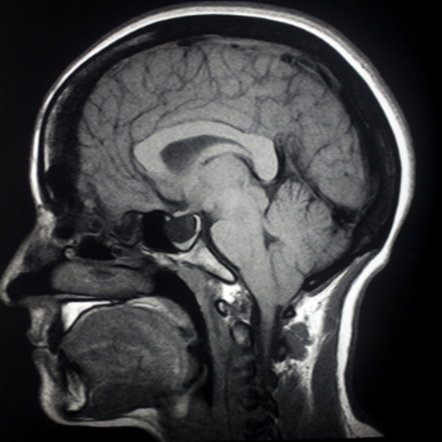
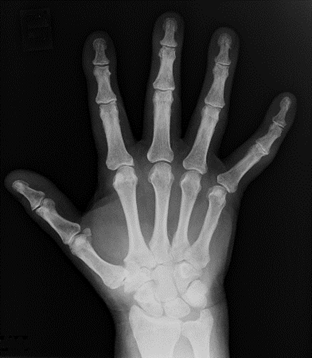
Een andere methode is het maken van röntgenfoto's (zie de foto linksonder). Hierbij wordt röntgenstraling door het lichaam geschenen. Als deze straling het lichaam in geschenen wordt, dan zal een deel worden geabsorbeerd en een deel worden doorgelaten. Hoeveel er wordt geabsorbeerd hangt af van het soort stofwaar de straling doorheen gaat en van de dikte van deze stof. Door de doorgelaten straling op te vangen op een fotografische plaat kan dan een röntgenfoto worden gemaakt. Doordat spierweefsel bijvoorbeeld meer röntgenstraling doorlaat dan bot, kunnen we de botten in het menselijk lichaam hiermee duidelijk in kaart brengen.
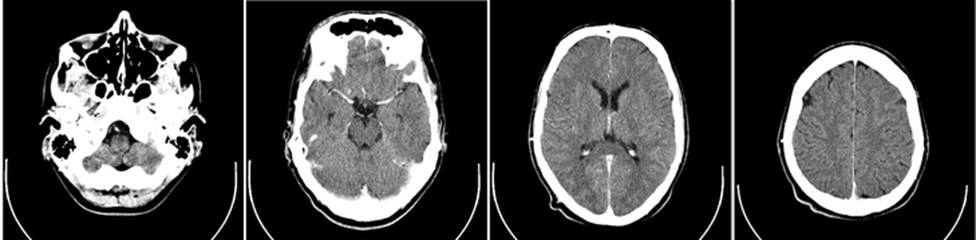
Ook bij een CT-scan wordt gebruik gemaakt van röntgenstraling. Hier worden meerdere metingen gecombineerd om een doorsnedefoto van het menselijk lichaam te maken. Series van deze doorsnedes kunnen gecombineerd worden tot een 3D weergaven van het menselijk lichaam. Hieronder zien we bijvoorbeeld doorsnedes van de hersenen.
Hoeveel straling er wordt doorgelaten bij het maken van een röntgenfoto hangt af van de halveringsdikte van verschillende materialen. De halveringsdikte van bot is bijvoorbeeld kleiner dan dat van spierweefsel en dit zorgt voor het contrast op de foto.
De halveringsdikte staat voor de afstand die straling kan afleggen door het materiaal totdat de helft van de straling geabsorbeerd is. De intensiteit van de straling neemt dus elke halveringsdikte met 50% af. In formuletaal wordt dit:
|
… $$I_d = I_0 \left( \frac{1}{2} \right)^{n} \;\;\;\;\; \text{met:} \;\; d = n \times d_{1/2}$$
|
De halveringsdikte hangt niet alleen af van het soort stof, maar ook van de energie van de straling. Een aantal halveringsdiktes zijn te vinden in BINAS 28F voor verschillende hoeveelheden energie. Let erop dat de halveringsdikte hier wordt gemeten in centimeter.
|
VWO |
||||||
|
|
||||||
|
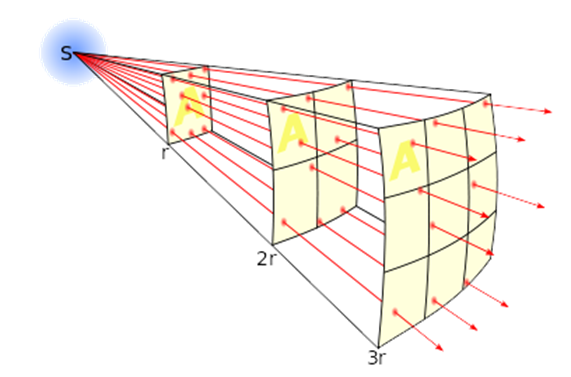
$$I = \frac{P_{bron}}{4\pi r^2}$$
|
||||||
|
De eenheid
van de intensiteit is hier joule per seconde per vierkante meter. Dit staat
dus voor de hoeveelheid joule die per seconde op een vierkante meter valt op
een bepaalde afstand r van de bron.
|
|
|
|
1. Zoek de halveringsdikte op van röntgenstraling dat door water heen schijnt met een kinetische energie van 0,1 MeV. Noteer ook in welke eenheid de halveringsdikte wordt gegeven.
2. Thalliumscintigrafie is een techniek die gebruikt wordt om de doorbloeding van de hartspier te onderzoeken. In het onderzoek wordt thallium-201 gebruikt. Deze isotoop ontstaat via twee reacties. Eerst wordt thallium-203 beschoten met een proton. Bij deze reactie ontstaat de isotoop lood-201. Uit het radioactieve verval van lood-201 ontstaat vervolgens thallium-201. a. Geef van beide kernreacties de reactievergelijking. b. De isotoop thallium-201 is radioactief en vervalt via een proces dat K-vangst heet. Bij K-vangst neemt een atoomkern een elektron op uit de binnenste elektronenschil. Bij dit proces komt alleen γ-straling vrij. Ook bij andere radioactieve stoffen die vervallen onder uitzending van α-straling of β-straling kan γ-straling vrijkomen. Toch wordt er in dit onderzoek gekozen voor een radioactieve stof die vervalt via K-vangst. Leg uit waarom. c.
(VWO) De hoeveelheid radioactieve stof die in het onderzoek gebruikt
wordt, heeft een activiteit van 56 MBq. Thallium-201 heeft een halveringstijd
van 3,04 dag. d.
In de patiënten-informatie over thalliumscintigrafie
staat: 'Na afloop van het onderzoek blijft de radioactieve stof nog enige
tijd in uw lichaam, waardoor u een minimale hoeveelheid straling uitzendt. Om
personen in uw omgeving niet onnodig aan straling bloot te stellen, is het belangrijk
dat u op de dag van het onderzoek een armlengte afstand tot andere mensen
bewaart'.
e.
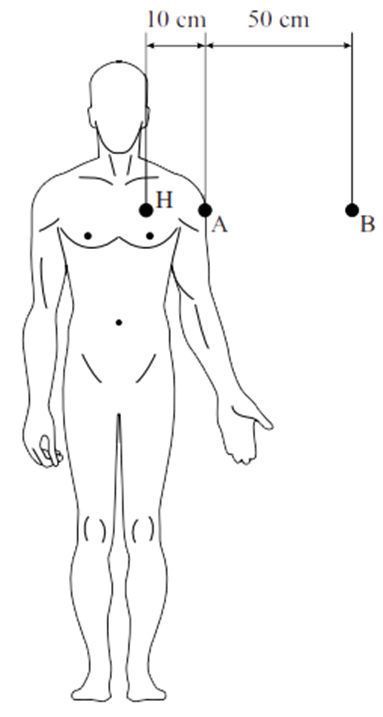
(VWO) Behalve door absorptie neemt de
stralingsintensiteit ook af dankzij de kwadratenwet. Bereken met welke factor
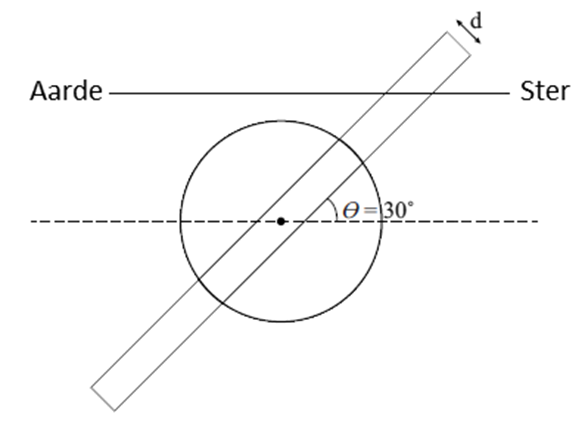
de stralingsintensiteit in punt B is afgenomen in vergelijking met punt A. 3.
Hieronder zien we een
schematische afbeelding van het zijaanzicht van de planeet Saturnus met zijn
ringen. Zoals je kunt zien bevinden de ringen zich gezien vanaf de aarde
onder een hoek van 30 graden.
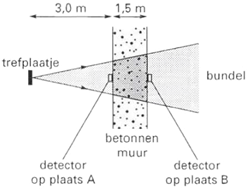
4. In een behandelkamer waarin röntgenstraling wordt gebruikt, is het de bedoeling dat zo weinig mogelijk van deze straling doordringt tot buiten de kamer. De kamer is daarom voorzien van betonnen wanden van 1,5 m dikte. Als een evenwijdige bundel röntgenstraling op deze wand zou vallen, is de sterkte van de straling achter deze wand 1,0 x 104 maal zo zwak als die voor de wand. a.
b.
(VWO) Uit het trefplaatje komt geen evenwijdige,
maar een divergerende bundel straling (zie de rechter afbeelding). De bron
staat op 3,0 m afstand van de muur. Bereken de verhouding van de stralingssterkte
voor en achter de muur zoals deze gemeten wordt door detectoren op plaats A
en B (zie de afbeelding). Houd hier rekening met de absorptie van het beton
en met de afname van de intensiteit van de straling door het divergeren van
de bundel. 5. (VWO) In deze opgave bekijken we een patiënt waarbij de botten in de benen worden onderzocht. Hierbij gebruikt men calcium omdat dit gemakkelijk door het lichaam opgenomen en getransporteerd wordt naar de botten. De patiënt krijgt een hoeveelheid van de instabiele isotoop calcium-47 toegediend. De vervalreactie van calcium-47 is:
$$^{47}\text{Ca} \rightarrow ^{47}\text{Sc} + \beta^- + \gamma$$
De gammastraling kan buiten het lichaam gedetecteerd worden. De arts kan zo zien of er met de botten iets bijzonders aan de hand is. a. Bij het begin van het onderzoek krijgt de patiënt een hoeveelheid calcium-47 toegediend met een activiteit van 2,5 MBq. Bereken de massa in kg van het calcium-47. b.
De benen van de patiënt worden onder een apparaat
gelegd dat de gammastraling meet. Als deze gammastraling van het bot naar de
detector beweegt, moet het door een stuk weefsel en een stuk lucht heen en
als gevolg wordt een deel van de straling geabsorbeerd. Hiervoor moet worden
gecorrigeerd met een correctiefactor. c.
(VWO) Een nadeel van deze onderzoeksmethode is de
stralingsbelasting van het bot. Deze ontstaat voornamelijk door absorptie van
β--deeltjes. Deze zijn niet alleen afkomstig van calcium-47 maar ook van
scandium-47 (dat ontstaat bij het verval van calcium-47). Hieronder zien we
het verloop van de gezamenlijke activiteit van beide isotopen in het bot van
het bovenbeen. Ga ervanuit dat op tijdstip t = 0 de calcium aankomt in het
bot.
|
|
|
|
6. Bij onderzoek naar de ziekte van Alzheimer wordt de PET-scan gebruikt. Daarbij spuit men bij de patiënt een speciale stof in die het C-11-isotoop bevat. Deze stof bindt het C-11-isotoop aan plaatsen in de hersenen waar de ziekte van Alzheimer zit. Het C-11-isotoop verkrijgt men door versnelde protonen op N-14 te schieten. a. Geef de kernreactievergelijking van de productie van het C-11-isotoop uit N-14. b.
Het C-11-isotoop vervalt onder uitzending van een
positron. Het positron dat ontstaat remt in het hersenweefsel af tot (bijna)
stilstand, en annihileert dan met een elektron. Daarbij worden twee gamma-fotonen
met dezelfde frequentie in tegengestelde richting uitgezonden (zie de
onderstaande afbeelding).
|
| BINAS: | |
| 5 | Elektronvolt |
| 7 | Massa van proton, neutron en elektron |
| 7 | Atomaire massa-eenheid (u) |
| 25 | Isotopen (halveringstijd, type straling en stralingsenergie per deeltje) |
| 27D2 | Stralingsnormen |
| 28F | Halveringsdiktes |
| 29 | Beknopte beschrijving methoden medische beeldvorming |