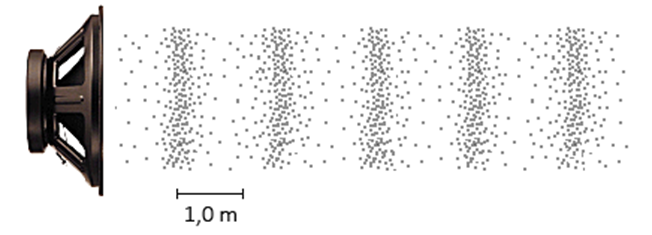Hoofdstuk 3
Geluid
§1 Geluid
In dit hoofdstuk gaan we trillingen en golven bestuderen. Hiermee kunnen we o.a. geluid begrijpen. In deze paragraaf bestuderen we het verschil tussen trillingen en golven.
Een trilling is het simpel heen en weer bewegen van een voorwerp. Een voorbeeld hiervan is het zogenaamde massa-veersysteem. Dit systeem bestaat uit een blokje aan een veer die heen en weer beweegt over een wrijvingsloos horizontaal oppervlak (zie de onderstaande afbeelding).
Zoals je kan zien beweegt het blokje heen en weer om het punt 'u = 0 m'. We noemen deze positie de evenwichtsstand. Als het blokje hier bevindt, dan bevindt de veer zich in zijn neutrale positie. Rechts van dit punt is de veer uitgerekt. Links van dit punt is de veer ingedrukt. De afstand van het midden van het blokje tot deze evenwichtstand noemen we de uitwijking (u). De maximale uitwijking die het blokje tijdens de beweging behaald noemen we de amplitude (A).
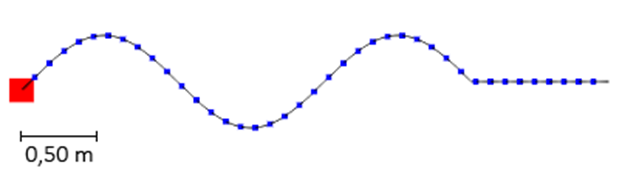
Hieronder zie je een animatie van een golf. Als je naar de website gaat, dan vind je de onderstaande afbeelding in de vorm van een animatie. Het oranje blokje aan de linkerkant beweegt in deze animatie omhoog en naar beneden. Aan het blokje zit een touw bevestigd. De trilling van dit blokje zorgt ervoor dat de rest van het touw ook in beweging komt. Elk stukje van het touw brengt het volgende stukje in beweging. We noemen een dergelijke kettingreactie een golf. Omdat de golf zich naar rechts verplaatst door het touw spreken we van een lopende golf.
Hoewel de golf zelf naar rechts beweegt, doen de deeltjes waaruit het touw bestaat dit niet. In de animatie kan je goed zien dat de deeltjes alleen op en neer bewegen. Elk deeltje voert dus een trilling uit en al deze trillingen samen vormen een golf. In de bovenstaande animatie staat de beweging van de deeltjes dus loodrecht op de beweging van de golf. Dit type golf wordt een transversale golf genoemd.
Net als in een touw, kunnen ook in de lucht golven ontstaan. Dit worden geluidsgolven genoemd. Deze golven ontstaan als we een voorwerp in de lucht in trilling brengen. Een voorbeeld is het trillen van de conus van een speaker, het trillen van een gitaarsnaar of het trillen van stembanden.

Op de website kan je een animatie van geluidsgolven zien. Het trillende
voorwerp (links) botst tegen de omliggende luchtdeeltjes en deze luchtdeeltjes
botsen weer tegen de volgende deeltjes etc. De beweging van de luchtdeeltjes zorgt ervoor dat er gebieden
ontstaat met een hoge dichtheid (veel deeltjes) en met een lage
dichtheid (weinig deeltjes). Deze gebieden van hoge en lage dichtheid
vormen de golf die in de animatie naar rechts beweegt. Het trommelvlies in ons
oor is gevoelig voor deze dichtheidsverschillen en zo nemen we geluid
waar.

Als je de deeltjes in de animatie volgt, dan zie je dat alle deeltjes naar links en naar rechts bewegen om een evenwichtsstand. Elk deeltje voert dus een trilling uit. De beweging van al deze deeltjes samen zorgt voor een lopende golf die naar rechts beweegt. De deeltjes bewegen in dit geval evenwijdig aan de richting van de golf. We noemen dit longitudinale golven.
Geluidsgolven komen niet alleen in lucht voor. In elk materiaal kunnen geluidsgolven ontstaan. In metalen, bijvoorbeeld, kunnen geluidsgolven zelfs nog sneller voortplanten dan in de lucht. De stof waarin de geluidsgolven zich verplaatsen noemen we het medium. Als een ruimte geen medium bevat, dan spreken we van een vacuüm. In een vacuümruimte kan geluid niet voortplanten.
|
|
|
1. Noem minstens drie geluidsbronnen.
2. Waarom heeft geluid een medium nodig?
3. Leg uit wat het verschil is tussen een trilling en een golf.
4. Geluid wordt veroorzaakt door trillende voorwerpen. Wat trilt er als we spreken? En wat trilt er we een mug horen zoemer?
5. Een bel wordt aangezet in een ruimte die langzaam vacuüm wordt gepompt. Leg uit wat er met het geluid gebeurt?
6. Is een wave in een voetbalstadium een longitudinale of een transversale golf.
|
§2 Trillingen
In deze paragraaf gaan we een aantal eigenschappen van de trilling bestuderen, waaronder de trillingstijd en de frequentie.
In de vorige paragraaf hebben we gelezen dat geluid wordt veroorzaakt door het trillen van luchtdeeltjes. We kunnen deze trillingen zichtbaar maken met een oscilloscoop (zie de onderstaande afbeelding). De lijn in het oscilloscoopbeeld kan worden opgevat als een grafiek. Op de horizontale as staat de tijd (t) en op de verticale as de uitwijking (u). We spreken hier daarom ook wel van een (u,t)-diagram.
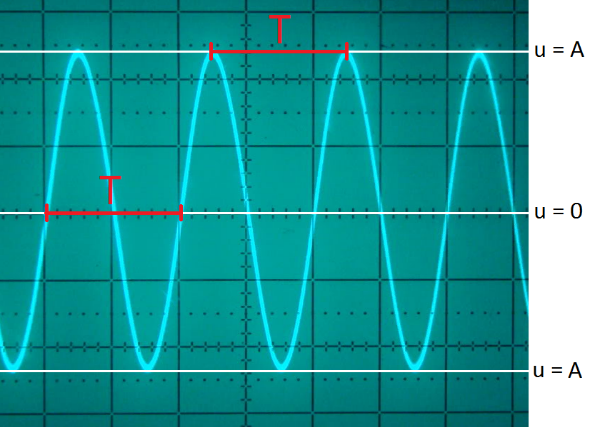
De bovenstaande trilling herhaalt zich in de tijd. We noemen een dergelijke beweging een periodieke beweging. De trillingstijd (T) geeft aan hoe lang het duurt voordat de beweging zich herhaalt. We noemen de trillingstijd ook wel de periode. In de bovenstaande afbeelding zien we twee manieren om de trillingstijd te meten.
De grootte van elk hokje op de horizontale as kan je instellen op de oscilloscoop en wordt gemeten in ms/div. Een waarde van 10 ms/div betekent bijvoorbeeld dat elk hokje op de horizontale as overeenkomt met 10 milliseconden.
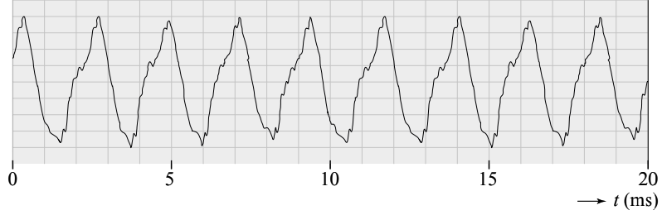
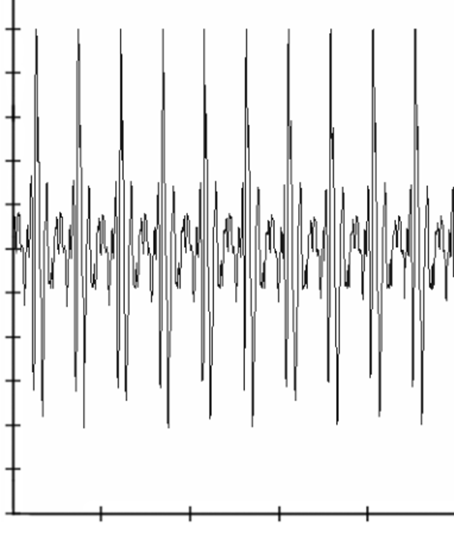
Hieronder zien we een ander voorbeeld van een periodieke beweging. In dit geval kijken we naar een toon geproduceerd door een saxofoon. De oscilloscoop is ingesteld op 10 ms/div. De tijdsduur behorende bij één trilling is in dit geval lastig nauwkeurig af te lezen. Het is hier daarom noodzakelijk om de trillingstijd van zoveel mogelijk trillingen tezamen te meten. Als we hier netjes meten, dan vinden we dat 9 trillingen 42 ms geduurd hebben (ga dit zelf na!). De trillingstijd is dus 42 / 9 = 4,7 ms = 0,0047 s.
Met de trillingstijd kunnen we ook de frequentie (f) bepalen. We meten de frequentie in hertz (Hz) en dit komt overeen met het aantal trillingen per seconde. Hier geldt:
|
… $$ f = \frac{1}{T} \,\,\,\,\,\textbf{(SI-eenheden)} $$…
|
Let erop dat je de trillingstijd in deze formule altijd in seconden invult. In het voorbeeld van de saxofoon vinden we:
$$ T = 4,7 \text{ ms} = 0,0047 \text{ s} $$
$$ f = \frac{1}{T}=\frac{1}{0,0047}= 2,1 \times 10^2 \text{ Hz}$$
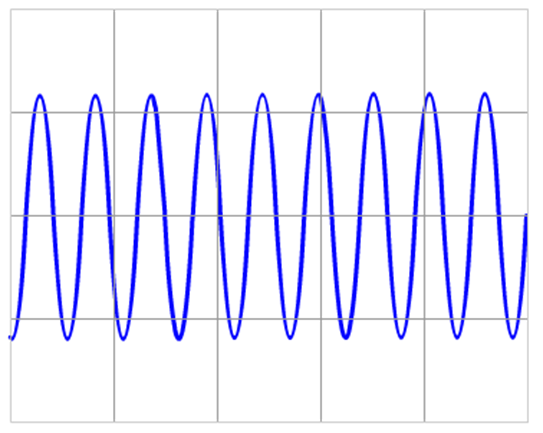
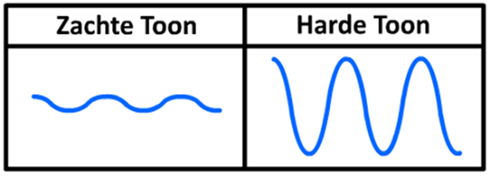
Laten we eens het oscilloscoopbeeld van een aantal tonen vergelijken. Hieronder zien we een oscilloscoopbeeld van een zachte en een harde toon. Zoals je kunt zien heeft een zachte toon een kleine amplitude en heeft de harde toon een grote amplitude. De 'hardheid' van het geluid noemen we in de natuurkunde de geluidsterkte. We meten de geluidsterkte in decibel (dB).
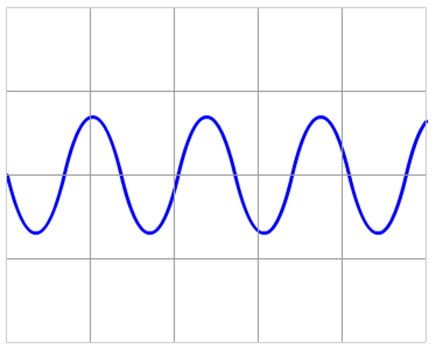
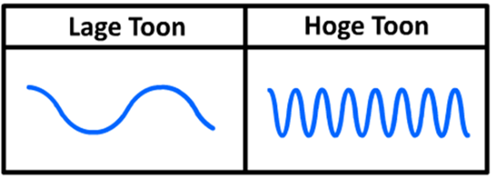
Hieronder zien we een oscilloscoopbeeld van een lage en een hoge toon. Zoals je kunt zien heeft een lage toon een lage frequentie (en een grote trillingstijd) en heeft een hoge toon een hoge frequentie (en een lage trillingstijd). De frequentie van een toon bepaald dus de toonhoogte van het geluid.
Bij muziekinstrumenten wordt de toonhoogte meestal niet met behulp van de frequentie weergegeven, maar met noten. De noot a heeft bijvoorbeeld een frequentie van 440 Hz. Hieronder zien we de frequentie van een aantal noten.
|
Noot |
Frequentie (Hz) |
|
C |
261,63 |
|
D |
293,66 |
|
E |
329,60 |
|
F |
349,23 |
|
G |
392,00 |
|
A |
440,00 |
|
B |
493,88 |
|
|
|
1. Een luidspreker produceert een toon van 2035 Hz. Bereken de trillingstijd van deze toon in milliseconden.…
2. Een stemvork trilt 1000 keer in 5 seconden. Bereken de frequentie en de trillingstijd van deze trilling.
3. Een boom waait 5x heen en weer in 10 seconden. Bereken de trillingstijd en de frequentie.
4. Een kolibrie beweegt tijdens het vliegen zijn vleugels erg snel op en neer. Hierdoor is een zoemend geluid te horen met een frequentie van 55 Hz. a. Hoelang duurt één trilling met zijn vleugels? b. De beweging wordt vastgelegd met een camera die 1100 beelden per seconde kan maken. In hoeveel frames wordt één trilling van de vleugel van de kolibrie vastgelegd?
5. Een saxofonist speelt twee tonen. De tweede toon heeft een grotere frequentie. Leg uit of de trillingstijd van de tweede toon groter of kleiner is.
6. Bij het aflezen van een oscilloscoopbeeld is het gebruikelijk om de tijdsduur van meerdere trillingen tegelijk op te meten. Vertel waarom dit zo is.
7. Gezoem van een mug heeft een hogere toonhoogte dan het gezoem van bijvoorbeeld een hommel. Welk insect beweegt zijn vleugels vaker op en neer?
8. Een pianotoets wordt eerst hard en dan zacht aangeslagen. a. Leg uit of de frequentie verschilt. b. Leg uit of de trillingstijd verschilt. c. Leg uit of de amplitude verschilt.
9. Een saxofonist speelt twee tonen. De eerste toon is laag en heel hard. De tweede toon is juist hoog en zacht. Teken hoe de twee tonen eruit zien op de oscilloscoop.
10. Een stemvork wordt aangeslagen. Na een tijdje wordt de toon steeds zachter hoorbaar. a. Leg uit of de frequentie verandert tijdens het zachter worden van het geluid. b. Leg uit of de amplitude verandert tijdens het zachter worden van het geluid.
11. Teken het (u,t)-diagram van een trillend voorwerp met een frequentie van 3,5 Hz en een amplitude van 2,5 cm.
12. Hieronder zien we het
oscilloscoopbeeld van een zuivere toon. De tijdsbasis is 5 ms/div. a. Bereken de frequentie van deze toon. b. Dezelfde toon heeft een octaaf lager een twee keer zo kleine frequentie. Teken het oscilloscoopbeeld van deze toon met dezelfde tijdsbasis.
13. Hieronder zien we het
oscilloscoopbeeld van een zuivere toon. De tijdsbasis is 0,2 ms/div. a. Bereken de frequentie van deze toon. b. Teken dezelfde toon als we de tijdsbasis op 0,4 ms/div zouden zetten.
14. Bepaal met behulp van BINAS de toon die hieronder is weergegeven:
|
§3 Golven (VWO)
In deze paragraaf gaan we rekenen met de golfsnelheid en de golflengte.
De snelheid van een golf meten we net als elke andere snelheid met de volgende formule uit het hoofdstuk ‘beweging’:
$$ v_{golf} = \frac{\Delta x}{\Delta t} $$
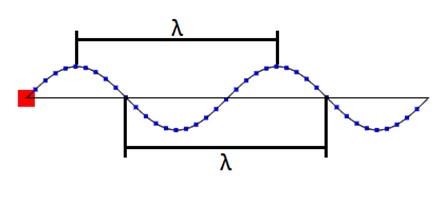
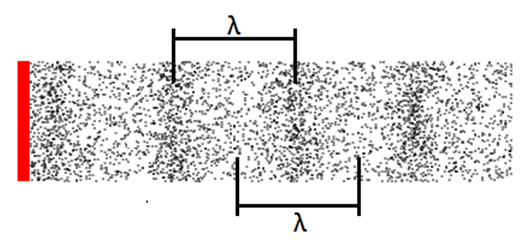
We kunnen deze formule ook nog herschrijven in twee andere vormen. We hebben hiervoor het begrip golflengte nodig. De lengte van een golf noemen we de golflengte (λ). Hieronder is de golflengte aangegeven bij zowel een golf in een touw als een geluidsgolf. Bij geluidsgolven is de golflengte gelijk aan de afstand tussen twee opeenvolgende plekken met een maximale of een minimale dichtheid.
Met de golflengte kunnen we de formule voor de golfsnelheid schrijven als:
|
… $$ v_{golf} = \frac{\lambda}{T} $$
|
Omdat f = 1/T, kunnen we deze formule ook schrijven als:
|
… $$ v_{golf} = \lambda f $$
|
In BINAS kan je voor een aantal stoffen de geluidsnelheid opzoeken. Deze geluidsnelheid is afhankelijk van de temperatuur. In de onderstaande tabel kan je bijvoorbeeld de geluidsnelheid in lucht vinden bij verschillende temperaturen. Let erop dat de temperaturen gegeven zijn in kelvin.
|
Temperatuur (K) |
Geluidsnelheid in lucht (103 m/s) |
|
233 |
0,307 |
|
253 |
0,319 |
|
273 |
0,332 |
|
293 |
0,343 |
|
313 |
0,354 |
|
333 |
0,365 |
Als in de vraag een temperatuur genoemd wordt, is dit dus vaak een aanwijzing dat de geluidsnelheid opgezocht moet worden.
|
|
|
1. Zoek de geluidsnelheid op in BINAS bij een temperatuur van 20 graden Celsius.
2. Je ziet tijdens een hevige storm een bliksemflits. 8 seconden later hoor je pas de bijbehorende knal. Bereken hoe ver de bliksem van je vandaan was. De temperatuur van de lucht is 20 oC.
3. Ook door gesteenten kunnen golven voortbewegen. De snelheid van deze golven is 5000 m/s. Het zijn deze golven die voor aardbevingen zorgen. Stel dat het epicentrum van een aardbeving 450 km van je vandaan ligt. Bereken hoelang het duurt voordat de aardbeving je bereikt.
4. In het wilde westen kwam het nog wel eens voor dat iemand zijn oor op de stalen trainrails legde om een trein van verre te horen aankomen (let op, tegenwoordig staan sommige rails onder stroom!). De geluidsnelheid in staal is 17× sneller dan de geluidsnelheid in lucht bij 20 oC. Bereken hoelang het duurt voordat het geluid van een trein op 5 km afstand hoorbaar is.
5. Met behulp van echo kan men bepalen hoe diep de zeebodem is. Men stuurt aan de onderkant van een schip een geluidspuls naar beneden en meet hoelang het duurt voordat de puls tegen de bodem reflecteert en terug komt bij het schip. Stel dat de echo er 0,59s over doet. Hoe diep is in dat geval de zeebodem.
6. Een persoon heeft zichtzelf per ongeluk opgesloten in een grote stalen kluis met een deur met een dikte van 20 cm. Buiten de kluis bevindt zich op 6,0 meter van de deur een bewaker. Om de aandacht van de bewaker te trekken, begint de persoon op de deur te kloppen. Bereken hoelang het heeft geduurd voordat de bewaker het geklop hoort.
7.
Hieronder zie je een golf die is ontstaan in een touw. De persoon die
de golf maakt beweegt het touw op en neer met een frequentie van 0,4 Hz.
Bereken de golfsnelheid van de golf in het touw.
8.
Hieronder zie je een geluidsgolf in een onbekend gas. De afbeelding
is 25× kleiner weergegeven dan ware grootte. De luidspreker produceert een
toon van 150 Hz. Bereken de geluidsnelheid in dit gas.
|
| BINAS: | |
| 15 | Geluidsnelheden |