Extra stof
Radiocommunicatie
In deze extra paragraaf gaan we radiocommunicatie begrijpen. Behalve bij de ouderwetse radio, gebruiken we radiocommunicatie o.a. bij mobiele telefonie en wifi. We gaan leren hoe je een schakeling kan maken waarmee je een zwak signaal uit de lucht kan versterken en hoe je van alle signalen die kriskras door elkaar door de lucht gaan, precies het juist kanaal kan ontvangen.
De wisselspanning
We beginnen met hoe we een radiosignaal kunnen detecteren. Radiostraling is een type licht dat buiten het zichtbare deel van het spectrum valt. Maar dan is de vraag, wat is licht? Licht is een elektromagnetisch golf. Als een lichtgolf tegen een stuk metaal komt, dan zorgt het elektrisch veld van de golf dat de vrije elektronen in het metaal heen en weer geduwd worden (zie de onderstaande animatie). Als gevolg ontstaat er een wisselspanning, waarbij de plus- en de minpool telkens omdraaien.
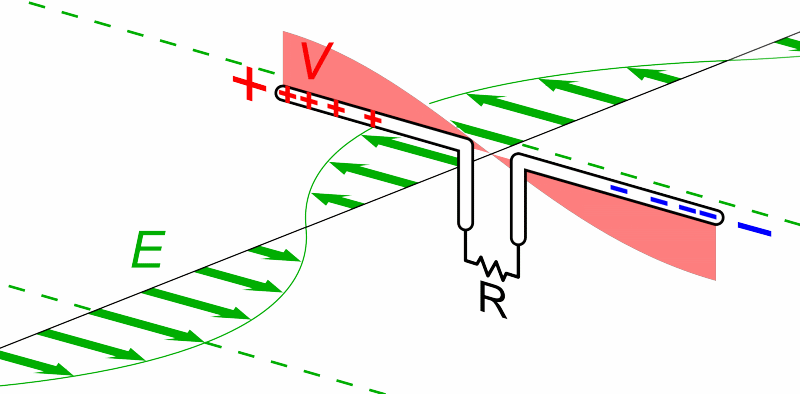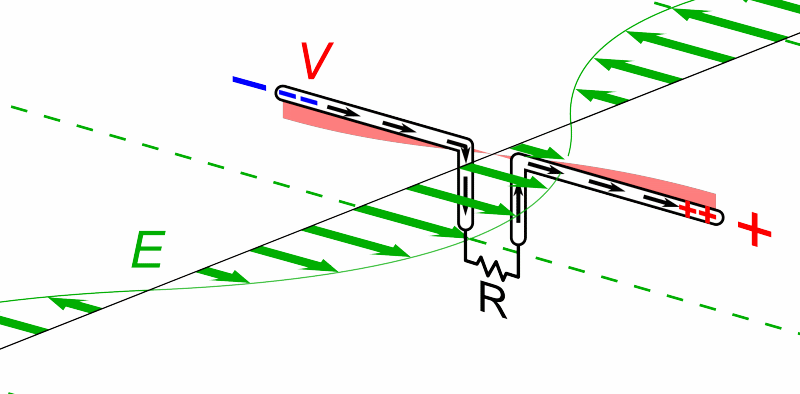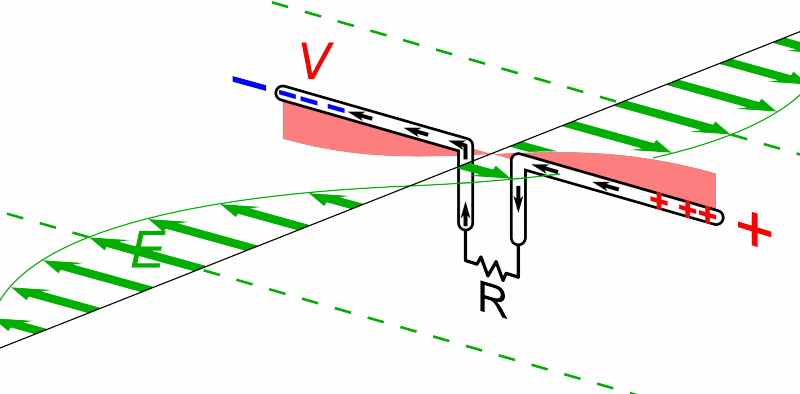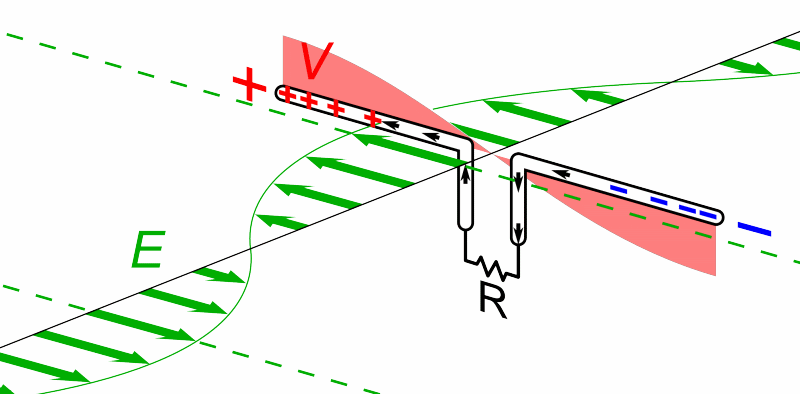
Wiskundig beschrijven we een wisselspanning als volgt:
| $$ u_{bron} = U_{bron} \cos(360^\circ f t) $$ |
In de onderstaande afbeelding zien we de bijbehorende grafiek. We zien hier hoe de spanning van de bron (ubron) varieert in de tijd (t). De letter "f" in de formule staat voor de frequentie. Dit geeft ons het aantal trillingen per seconde en wordt gemeten in hertz (Hz). Voor de cosinus vinden we de amplitude van de trilling. In dit geval is de amplitude gelijk aan de maximale spanning van de bron (Ubron). We gebruiken hiervoor de grote letter U.
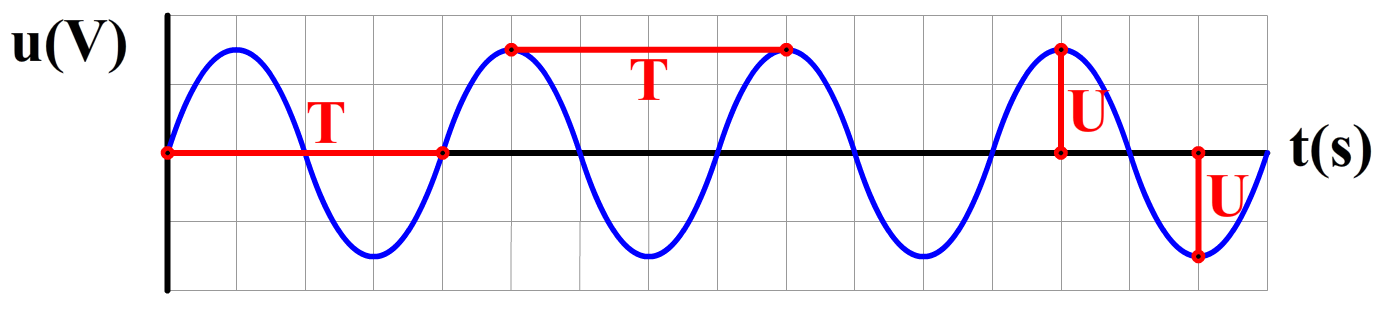
Om we de term "360° f" de hele tijd tegen gaan komen, is het handig dit beknopter op te schrijven als met behulp van de hoekfrequentie (ω):
$$ \omega = 360^\circ f $$De formule wordt dan:
| $$ u_{bron} = U_{bron} \cos(\omega t) $$ |
De weerstand
Laten we de wisselspanning eens aansluiten op een weerstand. Met de wet van Ohm (i = u/R), vinden we:
$$ i_R = \frac{u_R}{R} = \frac{U_R}{R} \cos(\omega t) $$Met I = U/R kunnen we dit omschrijven tot:
| $$ i_R = I_R \cos(\omega t) $$ |
Het blijkt handig om deze cosinusbewegingen weer te geven met behulp van een vector die roteert om de oorsprong met frequentie f en met een lengte gelijk aan de ampltide. Hieronder zien we dit gedaan voor zowel de stroomsterkte als de spanning. De plek waar de stippellijn de horizontale as raakt geeft de waarde van de stroomsterkte of de spanning op een bepaald tijstip.
Omdat zowel de stroomsterkte als de spanning dezelfde cosinusterm bevat, roteren beide vectoren synchroon. We zeggen dat de trillingen in fase bewegen.
De condensator
Het volgende onderdeel dat we nodig hebben is de condensator. Een condensator bestaat uit twee metalen plaatjes die elkaar net niet raken. Je kan dit onderdeel o.a. gebruiken als een simpele batterij. Als je een spanningsbron aansluit op een condensator, dan wordt de ene plaat positief en de andere plaat negatief (zie de onderstaande linker afbeelding). Als we daarna de spanningbron loskoppelen, dan blijven de ladingen op de condensator zitten zie de middelste afbeelding). Op deze manier kunnen we een beetje lading opslaan in de condensator. Als we dan bijvoorbeeld een lamp aansluiten, dan ontlaat de condensator en gaat de lamp branden (zie de rechter afbeelding). Als je de condensator flink hebt opgeladen, dan kan je hiermee een behoorlijke lichtpuls maken. Deze techniek wordt bijvoorbeeld gebruikt bij de flits van een camera.
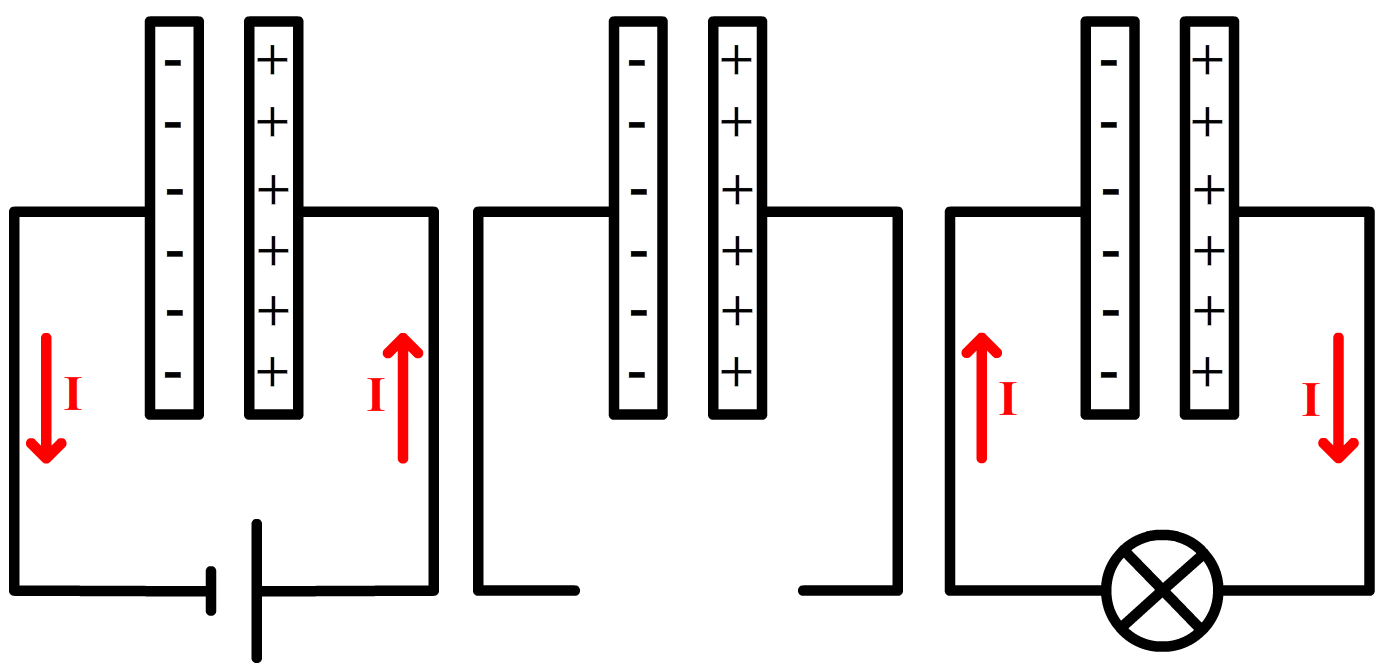
De spanning over de condensator hangt o.a. af van het oppervlak van de platen (A) en de afstand tussen de platen (d). Deze gegevens zitten verstopt in een grootheid die we de capaciteit (C) noemen. Er geldt:
$$ C = \frac{\epsilon_0 A}{d} $$De spanning hangt natuurlijk ook af van de hoeveelheid lading (q) die zich op de platen bevindt. Er geldt:
$$ u_C = \frac{q_C}{C} $$Als we deze formule omschrijven, en de spanning uitschrijven met uC = UCcos(ωt), dan vinden we:
$$ q_C = CU_{C}\cos(\omega t) $$De stroomsterkte kunnen we berekenen met de formule i = dq/dt. De stroomsterkte is dus de afgeleide van de lading naar de tijd. We vinden:
$$ i_C = \frac{dq_C}{dt} = \frac{d}{dt} \left( CU_C\cos(\omega t) \right) = -\omega CU_C\sin(\omega t) $$Met de wiskundige gelijkheid cos(x + 90°) = -sin(x), kunnen we de sinus weer terugschrijven naar een cosinus:
$$ i_C = \omega CU_C \cos(\omega t + 90^\circ) $$De term voor de cosinus is gelijk aan de amplitude van de stroomsterkte. We kunnen dit dus herschrijven als:
| $$ i_C = I_C \cos(\omega t + 90^\circ) $$ |
Als we de bovenste twee formules vergelijken, dan vinden we:
$$ I_C = \omega CU_C $$ $$ I_C = \frac{U_C}{X_C} $$Aan de formule I = ICcos(ωt + 90°) zien we ook dat de stroomsterkte 90° voorloopt op de spanning. Dit is goed te zien in de onderstaande animatie. Hoe komt dit? Als spanning over de condensator maximaal is, dan is de spanning dus even constant en stroomt er geen extra lading meer naar de condensator. De stroomsterkte is dan dus nul. Als de spanning maximaal aan het toenemen is (dat gebeurt bij de 0 V), dan neemt de lading op de condensator toe en hebben we dus een maximale stroomsterkte. De stroomsterkte en de spanning lopen dus niet meer in fase.
Laten we nu een weerstand en een condensator in serie aansluiten op een wisselspanning. We noemen dit een RC-schakeling (zie de onderstaande afbeelding).
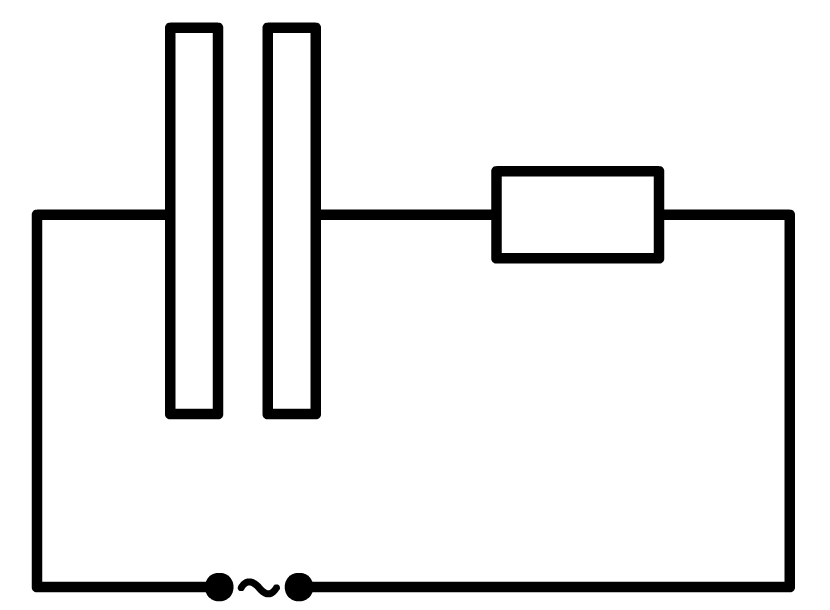
De maximale totale spanning Utotvinden we door de vectoren UR en UC uit de bovenstaande animatie bij elkaar op te tellen. Dit doen we met behulp van een parallellogram. In de animatie kan je het resultaat zien door de checkbox "Utot" aan te klikken. Omdat de vectoren loodrecht op elkaar staan, kunnen we de stelling van Pythagoras gebruiken om de totale spanning te vinden:
$$ U_{bron}^2 = U_R^2 + U_C^2 $$De spoel
Als laatste onderdeel hebben we een spoel nodig. Een spoel is een rondgewikkeld stukje draad. Om de werking van de spoel te begrijpen moet je weten dat om elke stroomvoerende draad een klein magneetveldje vormt. Als we een draad vaak omwikkelen, dan versterken deze magneetveldjes elkaar. Hoe sterk dit magneetveld wordt hangt o.a. af van het aantal windingen van de spoel (N) en de lengte van de spoel (l). Deze gegevens zitten verstopt in een grootheid die we de zelfinductie (L) noemen:
$$ L = \frac{\mu_0N^2}{l} $$De spanning hangt ook nog af van het volgende. Als de stroomsterkte door de spoel varieert, dan varieert ook het magneetveld dat ontstaat. Een varierend magneetveld zorgt voor het ontstaan van een elektrisch veld en dit elektrische veld geeft de ladingen in de spoel een extra duw. Als gevolg neemt de spanning over de spoel toe. De spanning is dus ook afhankelijk van de verandering van de stroom. Er geldt:
$$ u_L = L\frac{di_L}{dt} $$Als we aan beide kanten de integraal nemen en de spanning uitschrijven met uL = ULcos(ωt), dan vinden we:
$$ \int U_L\cos(\omega t) \text{ dt} = Li_L $$Als we de integraal uitvoeren, dan vinden we:
$$ \frac{U_L}{\omega} \sin(\omega t) = Li_L $$Dit kunnen we omschrijven tot:
$$ i_L = \frac{U_L}{\omega L} \sin(\omega t) $$Met sin(x) = cos(x - 90°) vinden we:
$$ i_L = \frac{U_L}{\omega L} \cos(\omega t - 90^\circ) $$De term voor de cosinus is gelijk aan de amplitude van de stroomsterkte:
| $$ i_L = I_L \cos(\omega t - 90^\circ) $$ |
Als we de bovenste twee formules vergelijken, dan vinden we:
$$ I_L = \frac{U_L}{\omega L} $$Aan de formule i = ILcos(ωt - 90°) zien we ook dat de stroomsterkte 90° achterloopt op de spanning. Dit is goed te zien in de onderstaande animatie. Hoe komt dit? Aan de formule uL = Ldi/dt zien we dat als de spanning maximaal is, dat dan de stroomsterkte door de spoel maximaal toeneemt (dit gebeurt bij de 0 A). Ook zien we dat als de spanning over de spoel nul is, dat de stroomsterkte dat niet verandert. Dit gebeurt als de stroomsterkte maximaal is. Ook hier lopen de stroomsterkte en de spanning dus niet in fase.
De RLC-schakeling
Laten we nu een serieschakeling maken waarin een weerstand, een condensator en een spoel zijn aangesloten op een wisselspanning. We noemen dit een RLC-schakeling (zie de onderstaande afbeelding).
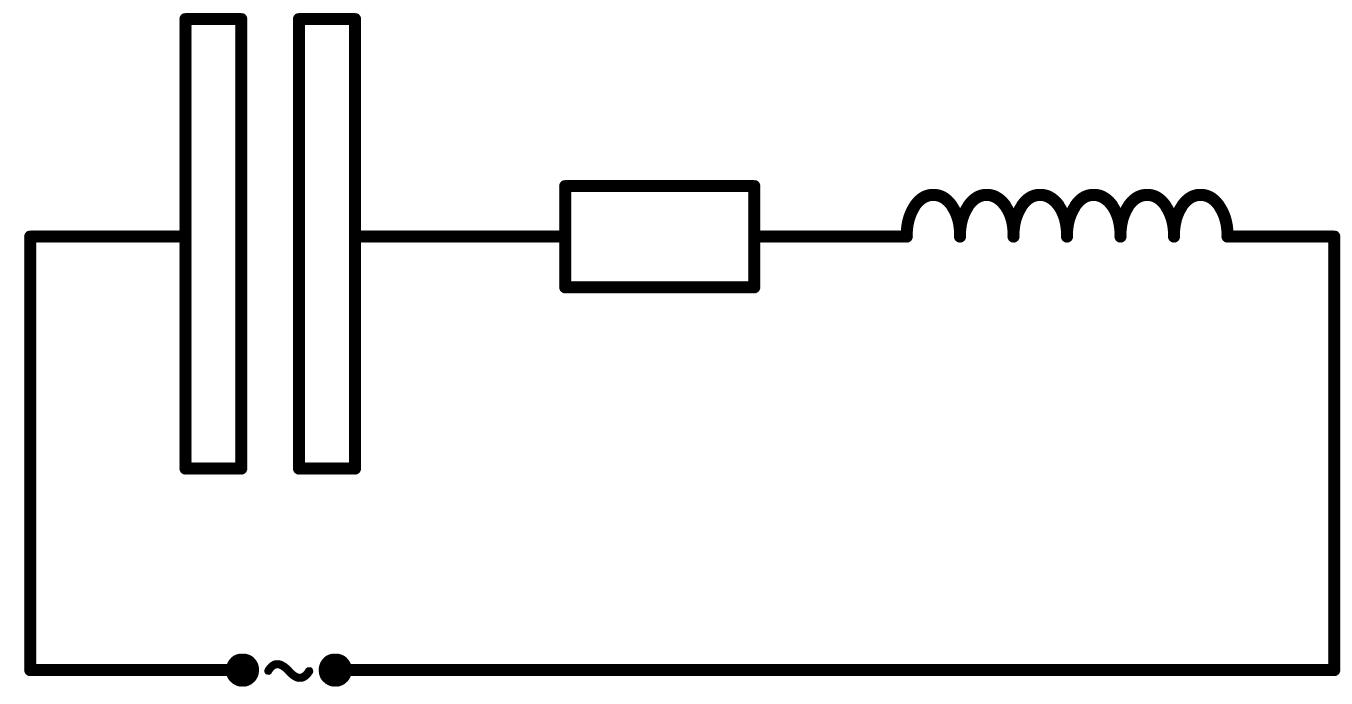
De maximale totale spanning Utot vinden we door de vectoren UR, UC en UL uit de bovenstaande animatie bij elkaar op te tellen. Dit kunnen we in twee stappen doen. Eerst tellen we de twee vectoren UL en UC bij elkaar op. In de bovenstaande animatie zien we dat deze vectoren precies in tegengestelde richting lopen. We zeggen dat ze in tegenfase lopen. Als gevolg heffen ze elkaar deels op (UL - UC). De resultante van deze twee vectoren kunnen we daarna met een parallellogram optellen bij UR. Er geldt:
$$ U_{bron}^2 = U_R^2 + (U_L-U_C)^2 $$We vullen hier nu in dat UR=IR, UC=I/(ωC) en UL=IωL:
$$ U_{bron}^2 = I^2R^2 + (I\omega L - I/(\omega C))^2 $$Dit kunnen we omschrijven tot:
| $$ I = \frac{U_{bron}}{\sqrt{R^2 + (\omega L - 1/(\omega C))^2}} $$ |
De radio
Aan de bovenstaande formule zien we dat de stroomsterkte I maximaal wordt als de de term "(ωL - 1/(ωC))2" minimaal is. Door het kwadraat kan deze term nooit negatief worden. De minimale waarde ervan is dus nul. Er geldt dan dus:
$$ \omega L - \frac{1}{\omega C} = 0 $$Dit kunnen we omschrijven tot:
| $$ \omega_{eigen} = \frac{1}{\sqrt{LC}} $$ |
Hieronder zien we de formule geplot met op de horizontale as de frequentie en op de verticale as de stroomsterkte:
Als je het hoofdstuk "Trillingen en Golven" bestudeerd hebt, dan herken je dit als een resonantiepiek. Laten we even kort bespreken wat dit is. Als je een schommel eenmalig een zetje geeft, dan gaat de schommel met een vaste frequentie trillen. We noemen dit de eigenfrequentie van de schommel. Als we de schommel precies in dit ritme een duwtje geven, dan zal de schommel binnen de kortste keren een grote amplitude krijgen. Bij elke andere frequentie zal je de schommel soms afremmen en soms versnellen en als gevolg bereik je nu niet een grote amplitude. Alleen als je de schommel (of welk ander trillend systeem dan ook) aandrijft in zijn eigenfrequentie neemt de amplitude drastisch toe. Dit noemen we resonantie.
Dan rest de vraag waarom hier sprake is van resonantie. Dit kunnen we begrijpen met de onderstaande animatie. We laden een condensator op en ontladen deze over een spoel. Normaalgesproken als we een condensator ontladen, bewegen de negatieve ladingen kortstondig naar de positieve plaat en daarna is de schakeling neutraal. In dit geval gebeurt iets anders. Eerder in dit hoofdstuk hebben we gelezen dat als de stroom door een spoel toeneemt, dat het magneetveld dat ontstaat zorgt voor een extra duwtje tegen de elektronen. Als gevolg worden zoveel negatieve ladingen naar de positieve plaat geduwd, dat deze plaat negatief wordt. Daarna ontlaadt de de condensator de andere kant op en geeft de spoel weer een extra duwtje, etc. De ladingen voeren in dit systeem dus een trilling uit met een bepaalde eigenfrequentie.
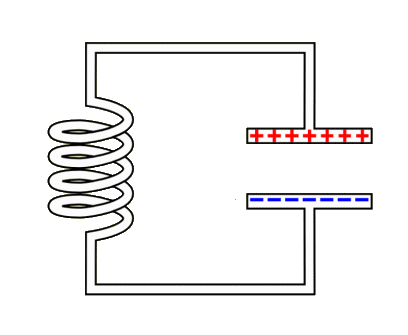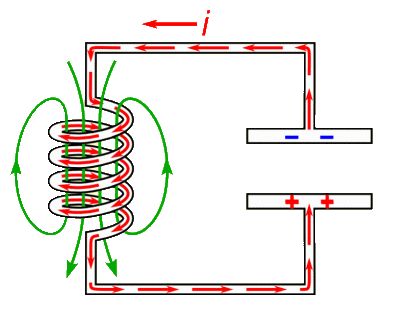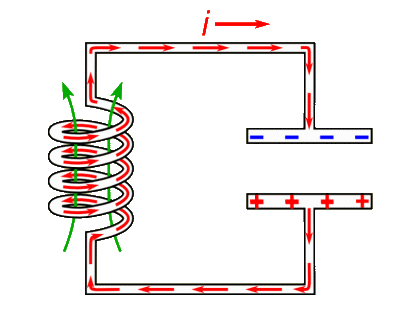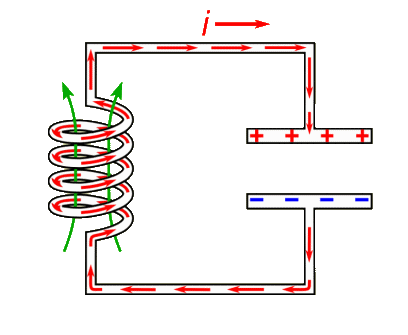
Nu komt de truc. Er zitten op elke moment een grote hoeveelheid verschillende elektromagnetische radiogolven in de lucht, elk met een andere frequentie. Als we onze schakeling afstellen, zodat de eigenfrequentie van onze schakeling gelijk is aan de frequentie van het signaal, dan zal dit signaal worden versterkt, terwijl de andere signalen worden gedempt, net als bij het aanduwen van de schommel.
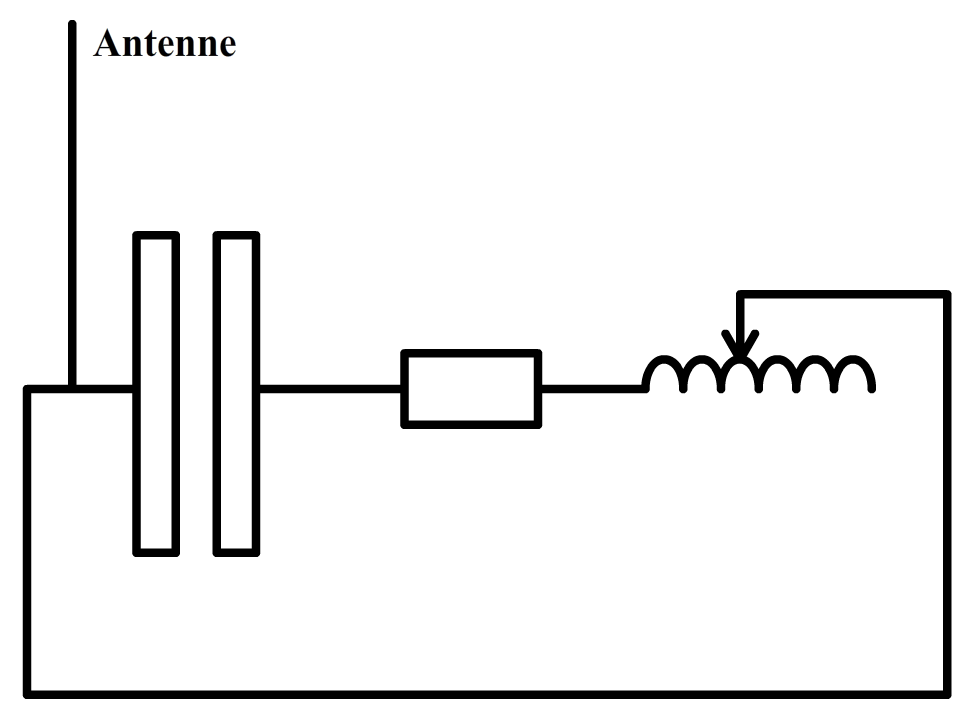
Eerder in deze paragraaf hebben we gezien dat de eigenfrequentie van een RLC-schakeling afhangt van de L en de C. De L kunnen we bijvoorbeeld veranderen door het aantal windingen van de spoel te variërenl. In de onderstaande afbeelding zien we een schakeling waarbij dit mogelijk is. Ook hebben we hier in plaats van het gebruikelijke tekentje voor de wisselspanning een antenne getekend. Dit is niets anders dan een lange draad waarmee we veel van het radiosignaal kunnen opvangen.