Poolcoördinaten

Bewegings vergelijkingen

Behoudswetten

Wetten van Kepler

Lagrangiaanse mechanica

Golfvergelijking

Fourier transformaties

Maxwell vergelijkingen

Bohratoom

Schrödinger vergelijking

Dirac vergelijking

Padintegralen

De ideale gaswet

wetenschaps filosofie

Statistiek

Radiocommunicatie

Extra stof hoofdstuk warmte
Druk

In het hoofdstuk kracht hebben we gelezen dat als we op de grond staan, dat we dan een zwaartekracht uitoefenen op de grond. De grootte van deze kracht wordt gegeven door:

$$ F_z = mg $$

Als we met beide beneden op de grond staan, dan wordt deze kracht verdeeld over de oppervlakte van onze voeten. Als we echter op onze tenen gaan staan, dan wordt dezelfde zwaartekracht verveeld over een veel kleiner oppervlak en dat voelt daarom een stuk minder fijn aan. Als we slechts op één teen zouden staan zou het helemaal pijnlijk zijn.

Behalve de kracht is het dus ook belangrijk over welk oppervlak deze kracht verdeeld wordt. We hebben dus een maat nodig voor de kracht die op een bepaald oppervlak wordt uitgeoefend en het begrip dat we hiervoor gebruiken is de druk. De formule voor de druk is:

De eenheid van de druk is newton per vierkante meter (N/m²), maar meestal wordt deze eenheid opgeschreven als Pascal (Pa). Newton per vierkante meter betekent letterlijk de hoeveelheid kracht er op een vierkante meter wordt uitgeoefend.

Laten we een aantal voorbeelden noemen die we met het begrip druk kunnen verklaren. We hebben allemaal wel eens gehoord dat als je op het ijs aan het lopen bent en het ijs gaat scheuren, het verstandig is om op je buik te gaan liggen en zo naar de kant te gaan. Dit komt omdat de zwaartekracht dan verspreid wordt over een groter oppervlak en de druk op het ijs dus kleiner wordt. Bij het snijden van een stokbrood willen we dat ons mes heel scherp is. Hoe scherper het mes is, hoe kleiner het oppervlak dat in contact komt met het brood en hoe groter de druk. We kunnen dan met een beetje kracht gemakkelijk snijden.

Laten we ook een rekenvoorbeeld bespreken. Stel dat een kubus met een massa van 100 kg en met zijdes van 50 cm stil ligt op de grond. Hoe groot is in dat geval de druk die de kubus op de grond uitoefent? Eerst berekenen we de zwaartekracht:

$$ F_z = mg = 100 \times 9,81 = 981 \text{ N} $$

De druk wordt:

$$ p = \frac{F}{A} = \frac{981}{0,50^2} = 3,9 \times 10^3 \text{ Pa} $$

Zelfs gassen kunnen een druk uitoefenen op voorwerpen. Het bekendste voorbeeld hiervan is de luchtdruk. De luchtdruk is groter dan mensen vaak denken. Lucht heeft een kleine dichtheid (slechts 1,23 kg/m³), maar de volledige massa van de atmosfeer boven ons is behoorlijk groot. De massa van de lucht boven een vierkante meter heeft een massa van ongeveer 10 000 kg! Als gevolg ervaren we per vierkante meter een luchtdruk van:

$$ p = \frac{F}{A} = \frac{10 000 \times 9,81}{1} \approx 1,0 \times 10^5 \text{ Pa} $$

Onder normale omstandigheden is de luchtdruk dus 10 × 10⁵ Pa.

Hoe hoger je in de atmosfeer komt, hoe lager de luchtdruk wordt. Dit komt omdat verder van de aarde de lucht moeilijker vastgehouden wordt door de zwaartekracht. In het onderstaande diagram kan je zien hoe de luchtdruk verandert met de hoogte. Deze grafiek wordt op een slimme manier gebruikt in een vliegtuig. Aan de buitenkant van het vliegtuig bevindt zich een drukmeter. Met de luchtdruk kan je dan in de grafiek aflezen hoe hoog het vliegtuig zich bevindt.

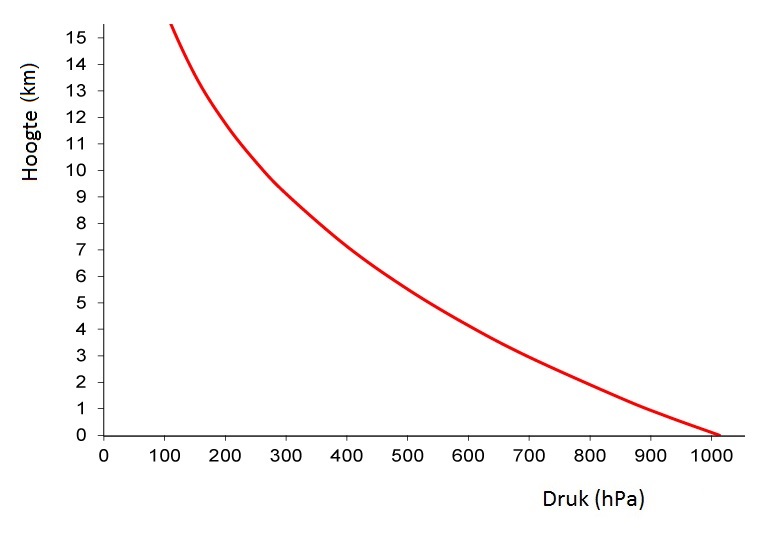
De luchtdruk is dus vrij groot, maar toch merken we er in het dagelijks leven relatief weinig van. Dit komt doordat de luchtdruk zichzelf meestal in evenwicht houdt. De luchtdruk die bijvoorbeeld op de bovenkant van de arm werkt, is even sterk als de luchtdruk die op de onderkant van je arm werkt etc.

Met een simpel experiment kunnen we demonstreren hoe sterk de luchtdruk daadwerkelijk is. In de volgende afbeelding zien we twee halve bollen die losjes tegen elkaar aan gelegd zijn. De lucht van buiten duwt de halve bollen tegen elkaar aan, maar de lucht aan de binnenkant biedt een even grote tegendruk, waardoor je in dit geval niets van de luchtdruk merkt. We kunnen de halve bollen daarom moeiteloos weer van elkaar af halen.

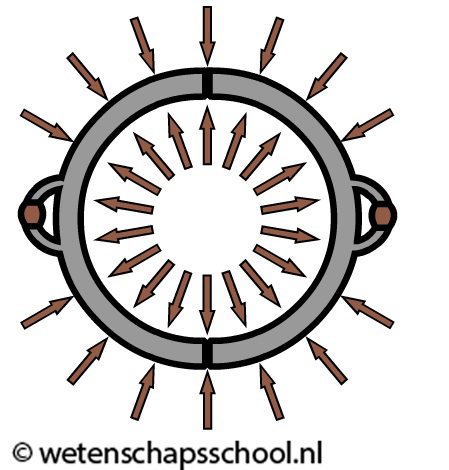
Als we echter de lucht aan de binnenkant wegpompen, dan ontstaat er aan de binnenkant van de bol een vacuüm. Een vacuüm is een lege ruimte zonder atomen. In deze ruimte zit dus zelfs geen lucht, want lucht bestaat uit atomen. De lucht drukt nu alleen nog vanaf buiten tegen de halve bollen. De tegendruk is weggevallen. Nu de luchtdruk niet meer in evenwicht is, kunnen we de echte kracht van de luchtdruk ervaren. Stel dat je aan beide kanten van de bol touwen verbindt en met een hele klas de bollen uit elkaar probeert te trekken, dan zal dit niet lukken. Dit is de kracht van de luchtdruk!

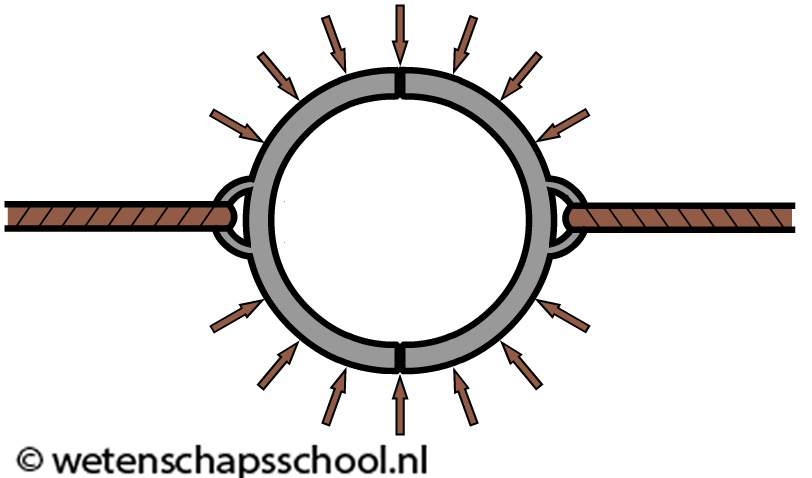
In de 17^de eeuw is dit experiment in het groot uitgevoerd. Zoals je in de onderste afbeelding kan zien werden zestien paarden ingeschakeld om de bollen uit elkaar te trekken, maar ook dit lukte niet. Zestien paarden tezamen zijn dus niet sterker dan de luchtdruk!

Eenzelfde soort effect zien we als we bijvoorbeeld een ballon in een vacuümruimte stoppen (zie het volgende filmpje). Doordat de luchtdruk van buitenaf wegvalt, neemt de druk van binnen in de ballon de overhand. Hierdoor zet de ballon uit.

Laten we ook een rekenvoorbeeld uitvoeren over het vacuüm. Stel we bevestigen een zuignap met een diameter van 10 cm tegen een plafond en we willen weten hoeveel massa we maximaal aan deze zuignap kunnen hangen zonder dat deze losschiet.

Over het algemeen werken er drie krachten op de zuignap. De zwaartekracht van het blok naar beneden, de luchtdruk naar boven tegen de zuignap aan en de normaalkracht naar beneden. Omdat het systeem in evenwicht is, moet dus gelden dat:

$$ F_{lucht} = F_z + F_N $$

Als we de massa steeds groter maken, dan wordt de zwaartekracht groter en om dit evenwicht in stand te houden, moet dan de normaalkracht kleiner worden. Bij de maximale is de normaalkracht nul. Er geldt dan:

$$ F_{lucht} = F_z $$

Voor de luchtdruk geldt:

$$ F_{lucht} = p_{lucht}A = p_{lucht} \times \pi \times r^2 $$ $$ F_{lucht} = 100 000 \times \pi \times 0,050^2 = 8,0 \times 10^2 N $$

De zwaartekracht is dus ook gelijk aan 8,0 × 10² N. De massa van het blok is dus gelijk aan:

$$ m = \frac{F_z}{g} = \frac{8,0 \times 10^2}{9,81} = 81 kg $$

We kunnen de luchtdruk ook verder verhogen. Een simpele manier om dit te doen is door de lucht samen te persen. Hoe dichter luchtmoleculen op elkaar worden gedrukt, hoe sterker ze tegen voorwerpen aanduwen. Hieronder is een cilinder getekend met daarin een zogenaamde zuiger. De zuiger is een schijf die vrij naar boven en naar beneden kan bewegen in de cilinder. Er werken nu twee soorten druk op de lucht in de cilinder. Ten eerste oefent de zwaartekracht van de zuiger zelf een druk uit en de ten tweede druk ook de luchtdruk boven de cilinder de zuiger naar beneden.

Stel dat de zuiger een massa heeft van 2,0 kg en een oppervlakte aan de onderzijde heeft van 10 cm². Wat wordt in dit geval de luchtdruk in de zuiger? We beginnen met de zwaartekracht:

$$ F_z = mg = 2,0 \times 9,81 = 19,6 \text{ N}$$

Nu rekenen we ook de druk uit (gebruik 10 cm² = 0,001 m²):

$$ p = \frac{F}{A} = \frac{19,6}{0,001} = 2,0 \times 10^4 \text{ Pa} $$

De druk van de lucht boven de zuiger kennen we al. Dit is de normale luchtdruk (100 000 Pa). De totale druk die op de zuiger werkt is dus:

$$ p_z + p_{lucht\; buiten} = p_{lucht\; binnen}$$ $$ 19 620 + 100 000 = 119 620 \text{ Pa} $$

Als we de zuiger loslaten, dan oefent de zuiger dus een druk uit die groter is dan de luchtdruk in de cilinder. Als gevolg van dit drukverschil zal de zuiger inzakken. Hierdoor neemt de druk in de cilinder toe. Dit proces gaat door totdat de luchtdruk in de cilinder gelijk is aan de druk die de zuiger op deze lucht uitoefent. De krachten zijn nu in evenwicht.

Maak met behulp van de formule p = F/A duidelijk waarom:

1. ... je op het ijs moet gaan liggen als je denkt dat het ijs kan breken.
2. ... het niet handig is om met hoge hakken over het strand te lopen.
3. ... je een brood het best kan snijden met een scherp mes.

Een zware bloempot wordt op een tafel gezet. De pot heeft een massa van 40 kg. De oppervlakte van de vaas dat de tafel raakt is 1,0 dm² groot. Hoe groot is de druk die op de tafel wordt uitgeoefend?

Als je de pot nader bestudeerd blijkt dat niet de hele dm² aan de onderkant de tafel raakt. Zoals in de afbeelding hieronder te zien is, is slechts een ring van 3,0 cm in aanraking met de tafel. Hoe groot is de druk op de tafel?

De luchtdruk is gemiddeld 1,0 × 10⁵ Pa. Deze druk voelen wij elk moment tegen ons lichaam drukken. Bereken hoeveel kracht er op elke cm² van de lichaam werkt.

We hebben een zuiger met een diameter van 8,0 cm en een massa van 0,500 kg. De luchtdruk die op de zuiger werkt is 1,0 × 10⁵ Pa. Hoe groot is de druk in de zuiger?

Redeneren met luchtdruk en vacuüm.

Leg uit hoe de luchtdruk ontstaat aan de hand van het deeltjesmodel. Wat is de luchtdruk op zeeniveau en op welke hoogte is de luchtdruk nog maar de helft van deze waarde? In het hoofdstuk lezen we dat de luchtdruk erg groot is. Toch merken we in het dagelijks leven weinig van deze kracht. Waarom zorgt deze kracht er bijvoorbeeld niet voor dat onze borstkast in elkaar wordt gedrukt? Een half opgeblazen ballon wordt in een ruimte gestopt die vacuüm kan worden gepompt. Als de vacuümpomp aan wordt gezet, wordt de ballon uit zichzelf groter. Leg uit hoe dit komt. Gebruik hiervoor de begrippen druk en tegendruk. Als je met de auto van een berg rijdt, kan je last krijgen van je oren. Dit komt door het verschil in luchtdruk van de lucht buiten en binnen je oor. Aan welke kant is de druk het hoogst? Leg uit waarom water al kookt bij kamertemperatuur in een vacuüm ruimte. Heliumballonen worden gebruikt om metingen te doen hoog in de atmosfeer. Als je een heliumballon loslaat dan stijgt deze op. Tijdens het opstijgen zet de ballon flink uit. Hoe komt het dat de ballon opstijgt? Waarom zet de ballon uit bij het opstijgen? Als we een ballon verwarmen, dan zet de lucht uit. Vertel wat er gebeurt met de massa, het volume en de dichtheid van de lucht. Wat zal er gebeuren als je de ballon genoeg verwarmt (maar de ballon niet knapt)? Hieronder zien we hetzelfde flesje bij hoogte 4 km, 3 km en 300 m. Het flesje is tussen het nemen van de drie foto's niet open geweest. Verklaar wat er met het flesje is gebeurd. Een vliegtuig gebruikt een drukmeter om te achterhalen hoe hoog hij vliegt. De luchtdruk buiten het vliegtuig is op een gegeven moment 400 hPa. Wat is de hoogte van het vliegtuig op dat moment? Een ruimtepak zit vol met lucht om het lichaam onder druk te houden. Waarom is dit nodig? Waarom kan je niet gewoon met een zuurstofmasker de ruimte in?

Redeneren met luchtdruk en vacuüm.

De Wet van Archimedes

In deze paragraaf gaan we leren hoe druk in water werkt. Laten we beginnen met een experiment dat hieronder is weergegeven. In een bak water zijn twee gaten gemaakt op verschillende hoogten. Zoals je ziet schiet het water met een hogere snelheid uit het onderste gat. Er werkt hier blijkbaar een grotere druk dan bij het bovenste gat. Hoe dieper we ons dus in het water bevinden, hoe hoger de druk.

Een simpele manier een druk te meten in water is met behulp van een veer waarvan de veerconstante nauwkeurig bepaald is. Je zal dan merken dat hoe dieper dit meetapparaat zich in het water bevindt, hoe meer de veer in zal drukken. Het zal je wellicht verbazen dat de druk die je meet niet afhangt van de oriëntatie van het meetinstrument. De druk blijkt dus gelijk te zijn in alle richtingen (zie de onderstaande afbeelding).

In de onderstaande afbeelding zien we een bak met water. We bestuderen de krachten die werken op het deel van het water dat zich binnen de stippellijnen bevindt. Aan de bovenkant werkt hier de luchtdruk die het water naar beneden duwt. Aan de onderkant werkt een druk omhoog van het water. Er werken ook krachten aan de linker en rechter wand, maar deze heffen elkaar op. Als laatste werkt er ook nog een zwaartekracht op het water.

Omdat het water stilstaat moeten de krachten in evenwicht zijn. Er geldt dus:

$$ F_{diepte} = F_{lucht} + F_z $$

Met de formule p = F/A kunnen we de kracht die de lucht op dit water uitoefent schrijven als F_lucht = p_lucht × A. We kunnen de bovenstaande formule daarom schrijven als:

$$ p_{diepte} A = p_{lucht} A + mg $$

Als we beide kanten delen door A en de formule voor de dichtheid invullen voor m, dan vinden we:

$$ p_{diepte} = p_{lucht} + \frac{\rho_{water} Vg}{A} $$

Omdat V / A gelijk is aan de diepte van het water (d), vinden we:

Laten we als voorbeeld een berekening doen aan een onderzeeboot die zich op een diepte van 300 meter bevindt. Voor de dichtheid gebruiken we 1,03 × 10³ kg/m³, de dichtheid van zeewater. De formule wordt:

$$ p = 1,0 \times 10^5 + 1,03 \times 10^3 \times 9,81 \times 300 = 3,1 \times 10^6 \text{ Pa} $$

Als we dit vergelijken met de luchtdruk, dan vinden we:

$$ \frac{3,1 \times 10^6}{1,0 \times 10^5} = 31\times $$

De druk is hier dus 31x zo sterk als de luchtdruk! Dit betekent dat als je bijvoorbeeld een raam wilt bouwen in een onderzeeboot, dat je deze heel sterk moet maken om deze druk te kunnen weerstaan.

In de onderstaande afbeelding zien we een blok dat zich onder water bevindt. Omdat de onderkant van het blok zich dieper in het water bevindt, heerst hier een grotere druk dan boven aan het blok. Dit betekent dat de druk netto zorgt voor een kracht omhoog. We noemen dit de opwaartse kracht. We merken deze kracht bijvoorbeeld als we een opblaasbal onder water proberen te duwen. De opwaartse kracht levert hier een behoorlijke tegenwerking.

In de onderstaande linker afbeelding zien we links weer water dat zich bevindt binnen een stippellijn. Als het water stilstaat (en daar gaan we hier vanuit), dan moeten de krachten volgens de eerste wet van Newton op dit water in evenwicht zijn. De opwaartse kracht op dit water en de zwaartekracht op dit water moeten dus gelijk zijn:

$$ F_{op} = F_{z,water} $$

Stel dat we het water binnen de stippellijnen konden verwijderen en in plaats daarvan een voorwerp plaatsen van dezelfde grote (zie de rechter bovenstaande afbeelding). Aangezien het water buiten de stippellijn onveranderd is gebleven, oefent dit water dezelfde druk uit op dit voorwerp als dat het deed op het water binnen de stippellijn. Ook hier moet dus gelden dat de opwaartse kracht gelijk is zwaartekracht van het water (!) dat zich eerst op de plek van het blok bevond. We noemen dit het verplaatste water. Er geldt dus:

$$ F_{op} = F_{z,water} $$

Dit kunnen we uitschrijven tot:

$$ F_{op} = m_{water} g $$

Dit kunnen we uitschrijven tot de zogenaamde wet van Archimedes:

Of het blok dat we onder water hebben geplaatst zal drijven of zinken hangt af van de grote van de opwaartse kracht en de zwaartekracht van het blok zelf. Voor deze zwaartekracht geldt:

$$ F_{z,blok} = m_{blok}g = \rho_{blok} V_{blok} g $$

Er geldt dus:

$$ F_{z,blok} \lt F_{op} \;\;\;\; \text{ (drijven)} $$ $$ F_{z,blok} \gt F_{op} \;\;\;\; \text{ (zinken)} $$

Oftewel:

$$ \rho_{blok} V_{blok} g \lt \rho_{water} V_{water} g \;\;\;\; \text{ (drijven)} $$ $$ \rho_{blok} V_{blok} g \gt \rho_{water} V_{water} g \;\;\;\; \text{ (zinken)} $$

En dit kunnen we versimpelen tot:

$$ \rho_{blok} V_{blok} \lt \rho_{water} V_{water} \;\;\;\; \text{ (drijven)} $$ $$ \rho_{blok} V_{blok} \gt \rho_{water} V_{water} \;\;\;\; \text{ (zinken)} $$

Als het blok zich helemaal onder water bevindt, dan zijn V_water en V_blok aan elkaar gelijk. Het water binnen de stippellijn en het blok zelf hebben dan immers dezelfde grootte. In dat geval hangt het verschil tussen zinken en drijven dus alleen nog af van de dichtheid:

En dit is precies de regel die we in hoofstuk 1 hebben geleerd in de paragraaf 'drijven en zinken'.

Als laatste bestuderen we een voorwerp dat drijft (zie de onderstaande afbeelding). Een deel van dit voorwerp steekt boven het water uit en een deel bevindt zich onder water.

Als het voorwerp stil ligt, dan kunnen we er weer vanuit gaan dat de krachten in evenwicht moeten zijn. De zwaartekracht en de opwaartse kracht moeten dus ook hier in evenwicht zijn:

$$ F_{op} = F_{z,blok} $$

Als we dit uitwerken, dan vinden we:

$$ \rho_{water} V_{water} g = \rho_{blok} V_{blok} g $$

Dit kunnen we versimpelen tot:

$$ \rho_{water} V_{water} = \rho_{blok} V_{blok} $$

Dit kunnen we omschrijven tot:

Met deze formule kunnen we uitrekenen hoeveel procent van het voorwerp onder water zal liggen. Neem bijvoorbeeld een ijsberg. Met dit dichtheid voor ijs en zeewater vinden we:

$$ V_{water} = \frac{917}{1030} V_{ijsberg} $$ $$ V_{water} = 0,89 \times V_{ijsberg} $$

We zien hier dat slechts 89% van het volume van de ijsberg zich in het water bevindt. Een ijsberg bevindt zich dus voor het overgrote deel onder water (zie de onderstaande afbeelding).

De Ideale Gaswet

Eerder in dit hoofdstuk hebben we vertelt dat temperatuur een maat is voor de beweging van deeltjes in een stof. Ook zijn we ervan uitgegaan dat bijvoorbeeld de luchtdruk beschreven kan worden door het botsen van een onvoorstelbare hoeveelheid kleine deeltjes die we atomen noemen. Maar hoe weten we dit eigenlijk? In deze paragraaf gaan we deze essentiële vragen beantwoorden.

Hieronder is een experiment beschreven waarmee de snelheid van deeltjes in een gas gemeten kan worden. In een oven wordt een gas verwarmd en de atomen van het verwarmde gas schieten weg uit een gas door een vacuüm ruimte. In deze ruimte draaien wielen rond met daarin één kleine opening (zie de afbeelding). Afhankelijk van de snelheid waarmee deze wielen gedraaid worden kunnen alleen deeltjes met een specifieke snelheid een detector bereiken te achter het tweede wiel geplaatst is. De detector kan dan op deze manier de hoeveelheid deeltjes meten die met die specifieke snelheid aangekomen zijn. Rechts zien we een aantal grafieken waarbij we voor verschillende gassen de snelheidsverdeling zien.

Onderzoek naar deze verdeling wijst uit dat als we het kwadraat nemen van zo'n snelheidsverdeling en dan het gemiddelde van deze gekwadrateerde snelheden nemen, dat dan geldt dat:

$$ \bar{v^2} = \frac{3kT}{m} $$

Als we dit omschrijven, dan vinden we:

$$ kT = \frac{1}{3}m\bar{v^2} $$

Dit is gelijk aan: $$ kT = \frac{2}{3} E_{kin,gem} $$

Dit kunnen we omschrijven tot:

$$ E_{kin,gem} = \frac{3}{2}kT $$

We hebben hiermee laten zien dat de temperatuur dus inderdaad samenhangt met de beweging van de deeltjes (met de kinetische energie).

We hebben nu een essentiële formule gevonden, maar we hebben nog niet ontdekt waar de formule \(\bar{v^2} = 3kT/m \) nu eigenlijk vandaan komt. Dit kunnen we verklaren door deze formule te combineren met een andere formule die bij experimenteel onderzoek gevonden is - de zogenaamde ideale gaswet:

$$ PV = NkT $$

P is hier de druk van het gas, V het volume van het gas, N het aantal deeltjes in het gas, k een constante en T de temperatuur. Als we deze formule combineren met \(\bar{v^2} = 3kT/m \), dan vinden we:

$$ PV = \frac{1}{3}Nm\bar{v^2} $$

Deze formule kunnen we afleiden door de botsingen van de deeltjes in het gas te bestuderen. Volgens de paragraaf 'Newtoniaanse mechanica' in het hoofdstuk 'Mechanica' kunnen we de tweede wet van Newton schrijven als:

$$ F = \frac{\Delta p}{\Delta t} $$ $$ p = mv $$

Stel we bestuderen een gas in een doos met gelijke zijden L. Stel we bestuderen een deeltje in het gas dat heen en weer beweegt langs de x-as. Stel dat het deeltje bij de rechterwand vertrekt, botst tegen de linker wand en dan weer terugkeert naar de startpositie. Daarna begint de hele beweging weer opnieuw. Er geldt dan:

$$ \Delta p = p_{eind} - p_{begin} = (mv_x) - (-mv_x) = 2mv_x $$ De kracht die op de linker wand werkt tijdens deze beweging is dan: $$ F = \frac{2mv_x}{\Delta t} $$

Tijdens de hierboven beschreven beweging is een afstand van 2L afgelegd. Er geldt dus:

$$ \Delta t = \frac{2L}{v_x} $$

Voor de kracht bij de botsing vinden we dus:

$$ F = \frac{mv_x^2}{L} $$

Als we niet één, maar N deeltjes hebben, dan vinden we:

$$ F = \frac{mv_{x,1}^2}{L} + \frac{mv_{x,3}^2}{L} + ... + \frac{mv_{x,N}^2}{L} = \frac{m}{L}(v_{x,1}^2+v_{x,2}^2+ ... +v_{x,N}^2)$$

Als we het kwadraat van alle snelheden bij elkaar optellen en delen door het aantal deeltjes, dan vinden we het gemiddelde van het kwadraat van de snelheid:

$$ \bar{v^2} = \frac{(v_{x,1}^2+v_{x,2}^2+ ... +v_{x,N}^2)}{N} $$

Dit kunnen we herschrijven tot:

$$ N\bar{v^2} =v_{x,1}^2+v_{x,2}^2+ ... +v_{x,N}^2 $$

Als we dit in de formule voor de kracht stoppen, dan vinden we:

$$ F = \frac{Nm\bar{v^2_x}}{L} $$

De druk is gegeven door:

$$ P = \frac{F}{A} $$

De druk die alle deeltjes op de linker wand uitoefenen is dus gelijk aan:

$$ P = \frac{Nm}{AL}\bar{v^2_x} = \frac{Nm}{V}\bar{v^2_x} $$

In de laatste stap hebben we er gebruik van gemaakt dat het oppervlak van de linker wand maal de lengte van de doos het volume van de doos geeft.

We moeten nu nog één aanpassing doen. Niet elk deeltje zal een snelheidscomponent in de x-richting hebben. Een deeltje kan bijvoorbeeld ook alleen omhoog en naar beneden bewegen of naar voren en achteren door de doos. Omdat de snelheid van elk deeltje drie componenten heeft en omdat de deeltjes in willekeurige richting bewegen, zal dus slechts 1/3 van de deeltjes een component in de x-richting hebben. De druk op de linkerwand zal dus een factor 3 lager zijn dan we hierboven berekend hebben. We vinden dus:

$$ PV = \frac{1}{3}Nm\bar{v^2} $$

Dit is exact de formule die experimenteel was aangetoond! We hebben dus laten zien dat we de druk geheel kunnen begrijpen aan de hand van de botsingen tussen deeltjes met behulp van de tweede wet van Newton. Ook de begrippen temperatuur en druk kunnen dus netjes beschreven worden met Newtoniaanse mechanica.

We zijn nu ook in staat de soortelijke warmte voor de mono-atomaire gassen uit te rekenen. Neem bijvoorbeeld een mol argon. Dit heeft een massa van 39,95 gram en bestaat uit 6,022 × 10²³ deeltjes (het getal van Avogardo). Stel dat we deze deeltjes vanaf 0K opwarmen tot een temperatuur T, dan geldt:

$$ Q = mc_V \Delta T = mc_VT $$

c_v is hier de soortelijke warmte bij een constant volume (in BINAS vinden we de soortelijke warmte voor een constante druk).

Omdat deze warmte zal gaan zitten in de kinetische energie van de deeltjes, vinden we ook dat:

$$ Q = NE_{kin,gem} = \frac{3}{2}Nk_BT $$

Als we deze formules combineren, dan vinden we:

$$ c_V = \frac{3}{2}\frac{Nk_B}{m} $$

Als we de soortelijke warmte uitrekenen, dan vinden we:

$$ c_V = \frac{3}{2}\frac{6,022 \times 10^{23} \times 1,381 \times 10^{-23}}{0,03995} = 312 \text{ J/kg/K} $$

Dit is precies de waarde die we vinden als we dit experiment daadwerkelijk uitvoeren!