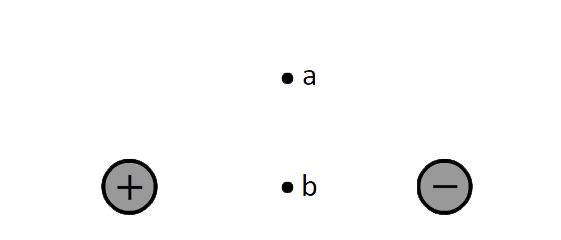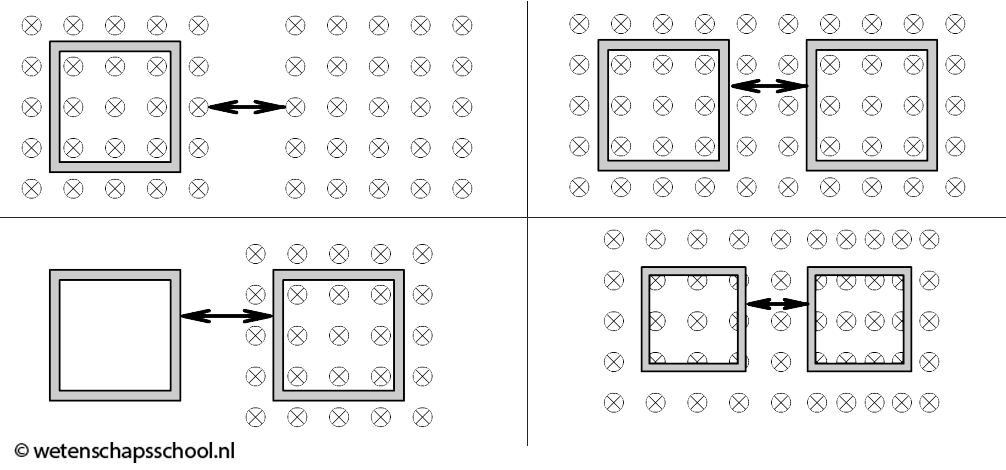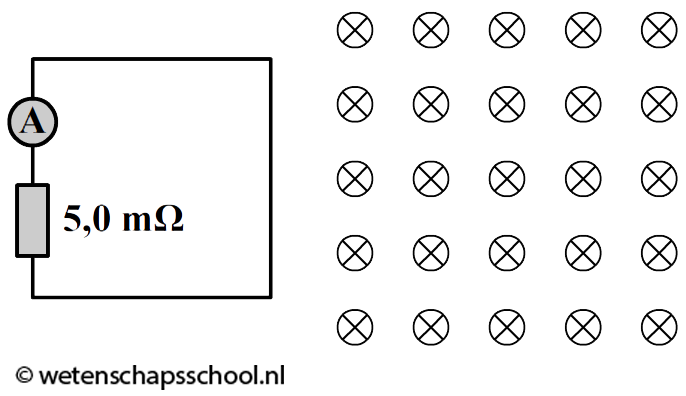Hoofdstuk 1
Magnetisme
§1 De elektrische kracht
§2 Magnetisme
§3 De lorentzkracht
§4 Inductie
§1 De elektrische kracht
In dit hoofdstuk gaan we elektrische en magnetische velden bestuderen en de krachten die deze velden kunnen uitoefenen. In deze paragraaf starten we met het elektrische veld.
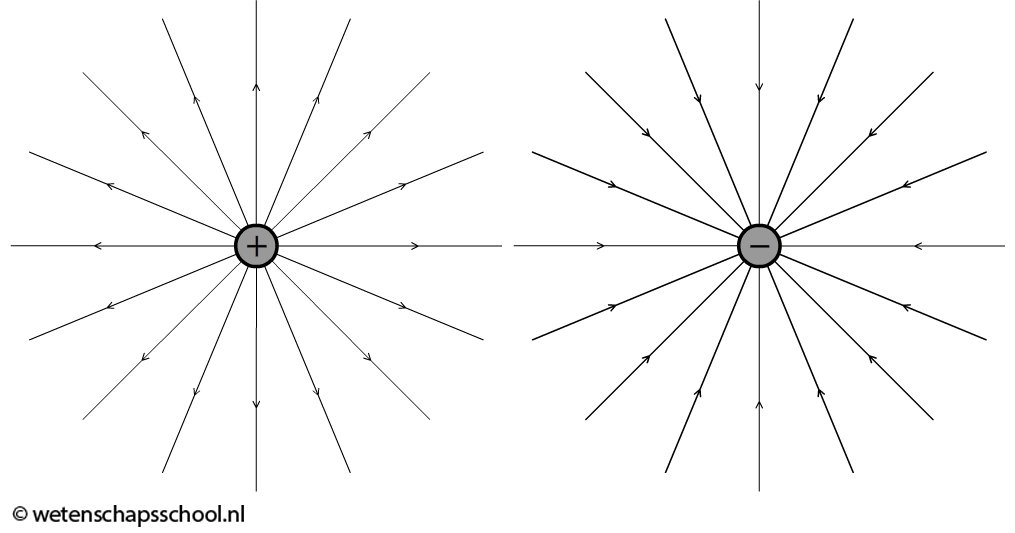
Alle voorwerpen met een lading worden omringd door een elektrisch veld. Met dit veld kunnen geladen deeltjes krachten op elkaar uitoefenen. Hieronder zien we het elektrisch veld om een positieve en een negatieve lading schematisch afgebeeld. We hebben het veld hier weergegeven met zogenaamde veldlijnen. Er geldt dat hoe dichter de lijnen op elkaar zitten, hoe sterker het veld is. In beide onderstaande gevallen is het veld dicht bij de ladingen het sterkst. Bij een positieve lading geven we het veld weer met pijlen die van de lading af wijzen. Bij een negatieve lading wijzen de pijlen juist naar de lading toe. We noemen deze velden, waarbij de veldlijnen naar één punt toe of van één punt afwijzen, radiale velden.
De sterkte van het elektrische veld noemen we de elektrische veldsterkte (E). Als een lading zich in een elektrisch veld bevindt, dan oefent dit veld een elektrische kracht uit gegeven door:
$$ F_{elek} = qE $$
|
Elektrische kracht (Felek)
|
newton (N)
|
|
Lading (q)
|
coulomb (C)
|
|
Elektrische veldsterkte (E)
|
newton per coulomb (N/C)
|
|
We kunnen ook direct te elektrische kracht tussen twee ladingen uitrekenen. We gebruiken hiervoor de zogenaamde wet van Coulomb:
$$ F_{elek} = \frac{fq_1q_2}{r^2} $$
|
Elektrische kracht (Felek)
|
newton (N)
|
|
Constante van Coulomb (f)
|
8,987551792 × 109 Nm2C-2
|
|
Lading (q)
|
coulomb (C)
|
|
Afstand tussen de ladingen (r)
|
meter (m)
|
|
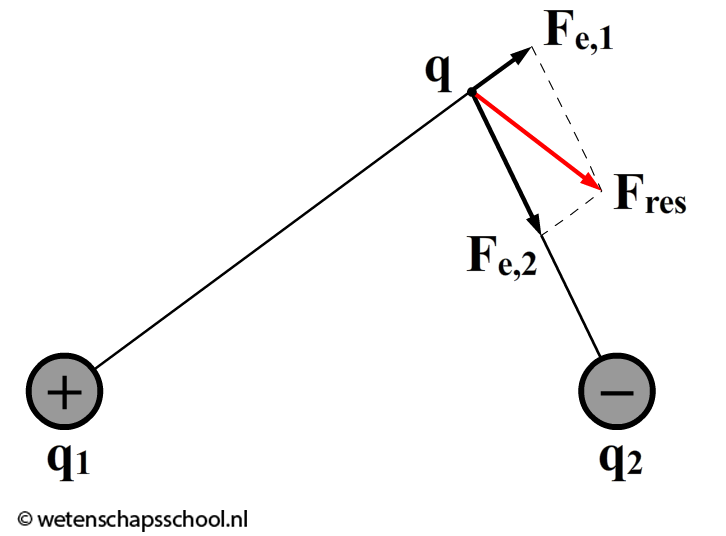
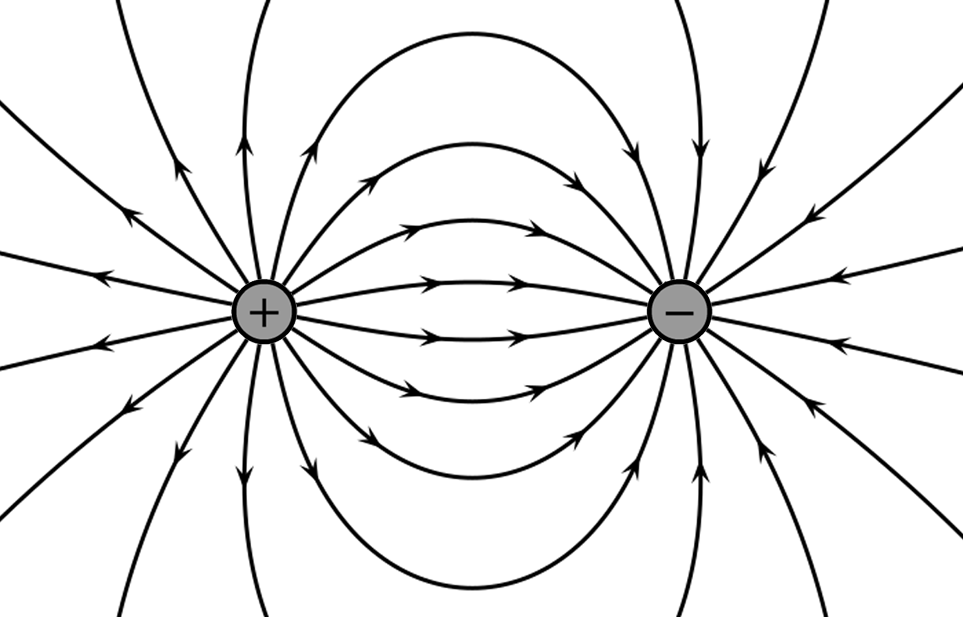
In de onderstaande linker afbeelding zien we een positieve lading q1 en een negatieve lading q2. Ook is er een positieve testlading q toegevoegd. Een testlading is een lading klein genoeg om de andere ladingen niet te beïnvloeden en wordt gebruikt om de sterkte van de elektrische kracht op een bepaald punt te meten. De testlading q ondervindt een afstotende kracht van lading q1 en een aantrekkende kracht van lading q2. Met een parallellogram kan dan de resulterende kracht op testlading q bepaald worden. Deze resulterende kracht geeft ons de richting van het elektrisch veld op de positie van de testlading. Als we dit experiment op veel punten uitvoeren, kan je hiermee de veldlijnen schetsen (zie de rechter afbeelding).
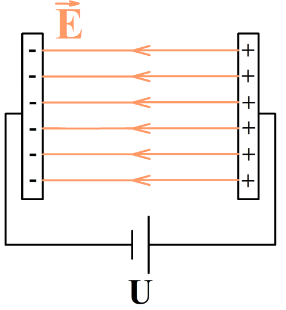
In de onderstaande afbeelding zien we het elektrisch veld dat ontstaat tussen twee condensatorplaten. Een condensator bestaat uit twee platen met op de ene een overschot aan positieve ladingen en op de andere een overschot aan negatieve ladingen. Tussen deze platen bevindt zich een homogeen elektrisch veld. Dit wil zeggen dat het elektrisch veld overal even sterk is en in dezelfde richting wijst (van de plus naar de min).
 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje is het elektrisch veld zichtbaar gemaakt voor zowel een puntlading als voor twee condensatorplaten. Het veld wordt zichtbaar door kleine stukjes griesmeel te laten drijven op olie. De stukjes griesmeel zijn aan één zijde positief geladen en de andere zijde negatief geladen. Als gevolg oefent het elektrische veld een kracht uit op de deeltjes die ze parallel laat lopen aan de veldlijnen.
|
 DEMO-VIDEO:
Elektrische velden
DEMO-VIDEO:
Elektrische velden
|
|
In de onderstaande afbeelding zien we een elektron die bij de negatieve plaat is geplaatst. Door het elektrisch veld zal het elektron naar de positieve plaat versnellen (de lading wordt immers afgestoten door de negatieve plaat en aangetrokken tot de positieve plaat). Merk op dat het elektron tegen de richting van het elektrische veld in beweegt. Een positief geladen deeltje zou juist met de veldlijnen meebewegen.
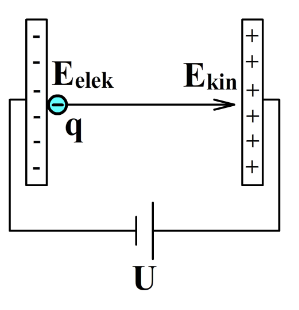
Omdat het elektron direct zal versnellen in het veld, weten we dat het elektron energie moet hebben. We noemen dit elektrische energie. De grootte van de elektrische energie wordt gegeven door:
$$ E_{elek} = qU $$
|
Elektrische energie (Eelek)
|
joule (J)
|
|
Lading (q)
|
coulomb (C)
|
|
Spanning over de platen (U)
|
volt (V)
|
|
Tijdens de beweging wordt elektrische energie omgezet in kinetische energie. Er geldt dus:
$$ E_{elek} = E_{kin} $$
 Voorbeeld
Voorbeeld
|
|
Vraag:
Bereken de snelheid van het elektron in een waterstofatoom. Ga er hierbij vanuit dat de afstand tussen het proton en het elektron in een waterstofatoom gelijk is aan 0,0529 nm.
Antwoord:
Omdat het elektron een cirkelbaan maakt om het proton, moet de elektrische kracht gelijk zijn aan de middelpuntzoekende kracht:
$$ F_{mpz} = F_{elek} $$
We kunnen deze vergelijking uitschrijven tot:
$$ \frac{mv^2}{r} = \frac{fq_1q_2}{r^2}$$
Aan beide zijden kunnen we een "r" wegstrepen:
$$ mv^2 = \frac{fq_1q_2}{r}$$
Voor de lading van het elektron en het proton gebruiken we de constante "e = 1,60218 × 10-19 J" (zie BINAS). We kunnen de rechterzijde hiermee versimpelen tot:
$$ mv^2 = \frac{fe^2}{r}$$
Als we de bovenstaande formule omschrijven, dan kunnen we hiermee de snelheid van het elektron berekenen. Voor de massa van het elektron gebruiken we "me = 9,10938 × 10-31 kg" (zie BINAS):
$$ v = \sqrt{ \frac{fe^2}{rm} } \;\;\;\;\;\;\;\;\;\;\;\;\; v = \sqrt{ \frac{ 8,98755 \times 10^9 \times (1,60218 \times 10^{-19})^2 }{9,10938 \times 10^{-31} \times 0,0529 \times 10^{-9} } } = 2,188 \times 10^6 \text{ m/s}$$
|
 INSTRUCTIE:
Elektrische kracht
INSTRUCTIE:
Elektrische kracht
 INSTRUCTIE:
Elektrische energie
INSTRUCTIE:
Elektrische energie
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je elektrische veldlijnen kan schetsen rond positieve en negatieve ladingen. Zorg dat je weet dat de veldlijnen wegwijzen van positieve ladingen en naar negatieve ladingen toewijzen.
- Zorg dat je kan rekenen met de formules "Felek = qE" en "Felek = fq1q2/r2". "f" is hier de constante van Coulomb (te vinden in BINAS) en "E" de elektrische veldsterkte in N/C.
- Zorg dat je de resulterende kracht op een testlading kan construeren met de parallellogrammethode.
- Zorg dat je weet dat tussen twee condensatorplaten een homogeen elektrisch veld vormt dat loopt van de positieve naar de negatieve plaat. Negatieve ladingen in dit veld bewegen tegen de veldlijnen in.
- Zorg dat je kan rekenen met energieomzettingen van geladen deeltjes in elektrische velden en dat je kan rekenen met de elektrische energie met behulp van de formule "Eelek = qU".
|
 Opdrachten
Opdrachten
|
-
(2p) Schets in de volgende twee afbeeldingen de elektrische veldlijnen:
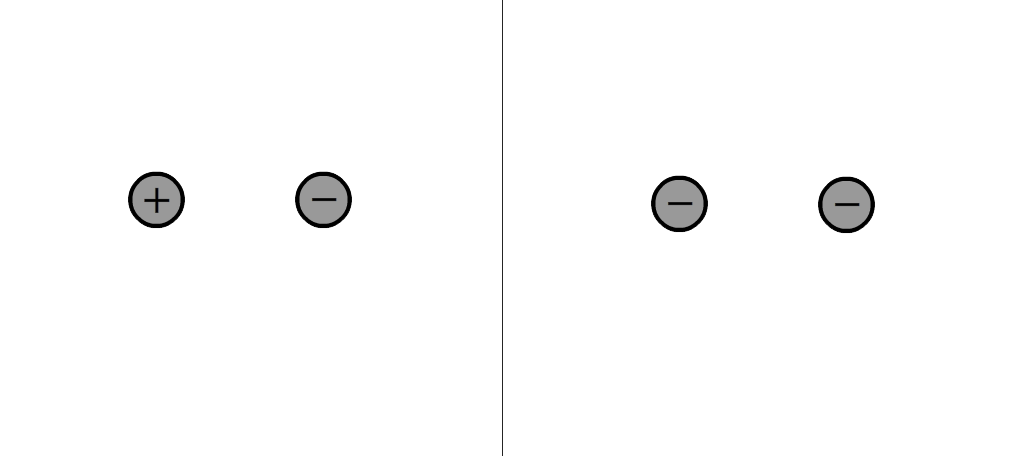
-
(6p) Hieronder zien we twee geladen bollen. De linker bol heeft twee keer zoveel lading als de rechter. Op de punten a en b wordt een positieve testlading geplaatst. Vind met een constructietekening de richting van het elektrische veld op punt a en b.
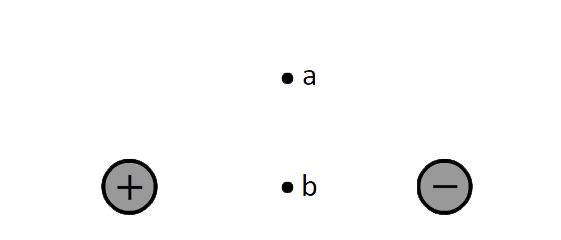
-
(3p) Hieronder zien we wederom twee geladen bollen. De linker bol heeft twee keer zoveel lading als de rechter. Vind met een constructietekening de richting van het elektrische veld op punt a.

-
Een leerling hangt twee pingpongballen op aan twee touwtjes met elk een lengte van 1,0 m. De touwtjes worden op dezelfde plek bevestigd aan het plafond. De pingpongballen worden omhuld met aluminiumfolie en worden voorzien van eenzelfde lading Q. Hierdoor stoten de twee ballen elkaar af en ontstaat er een hoek van 20 graden tussen de touwtjes (zie de onderstaande afbeelding. Deze afbeelding is niet op schaal afgebeeld). De pingpongballen met folie hebben elk een massa van 20 gram en blijven stil hangen op de plek die in de afbeelding is aangegeven.
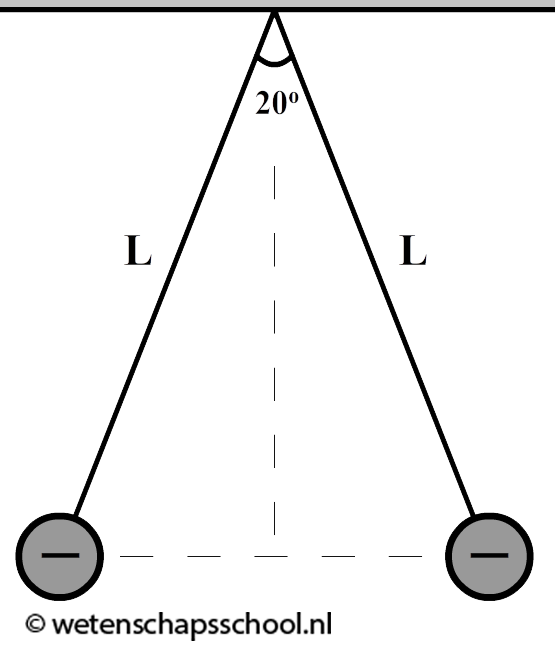
- (5p) Laat met een berekening zien dat de grootte van de elektrische kracht tussen de bollen gelijk is aan 0,034 N (Tip: teken eerst het krachtenevenwicht).
- (4p) Bereken de grootte van de lading Q.
-
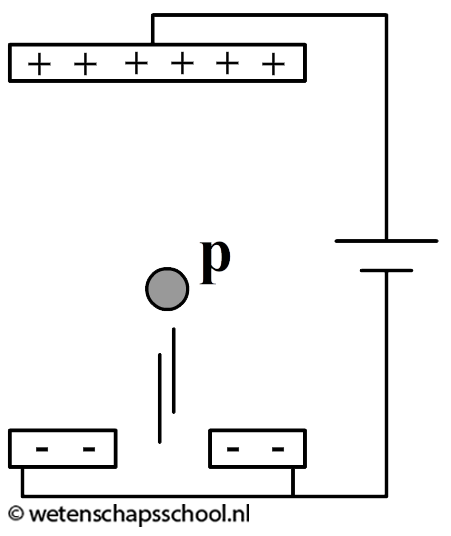
(6p) Een persoon plaatst een O2--ion met een massagetal van 16 tussen twee horizontale condensatorplaten die boven elkaar zijn geplaatst en waarover een kleine spanning van 10 nV staat (zie de onderstaande afbeelding). Voor het elektrisch veld tussen twee platen geldt:
$$ E = \frac{U}{d} $$
Bereken hoe groot de afstand tussen de platen moet worden om het zuurstof-ion te laten zweven.
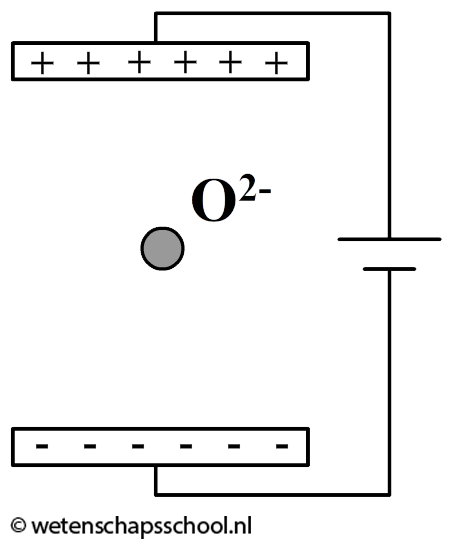
-
Een waterstofatoom bestaat uit een elektron dat in een cirkelbaan beweegt om een proton. In zijn grondtoestand maakt het elektron een cirkelbaan met een straal van 0,0529 nm.
- (4p) Bereken de grootte van het elektrische veld dat het elektron ondervindt van het proton.
- (3p) Laat zien dat de snelheid van het elektron gegeven wordt door:
$$ v = \sqrt{\frac{fe^2}{rm_e}}$$
-
(2p) Bereken hiermee de snelheid.
-
(4p) Een onderzoeker wil de snelheid van protonen meten afkomstig uit een radioactieve bron. Hij doet dit door protonen af te laten remmen in het elektrische veld tussen twee condensatorplaten (zie de onderstaande afbeelding. We bekijken deze opstellen van bovenaf).
Tussen de platen bevindt zich een diffuus gas dat oplicht als er protonen doorheen schieten. Hiermee kan worden gezien of het proton de andere zijde van de condensator kan bereiken of dat het proton eerder al tot stilstand komt. Het blijkt dat de protonen net de overkant van de condensator bereiken bij een spanning van 800 V. Bereken de oorspronkelijke snelheid van de protonen.
-
Hieronder is een röntgenbron weergegeven. De röntgenstraling wordt in dit apparaat geproduceerd doordat een gloeidraad een negatief geladen kathode verwarmd, waardoor elektronen loskomen uit het materiaal. Deze elektronen worden dan versneld richting de positieve anode. Als de elektronen tegen de anode botsen komen röntgenfotonen vrij.
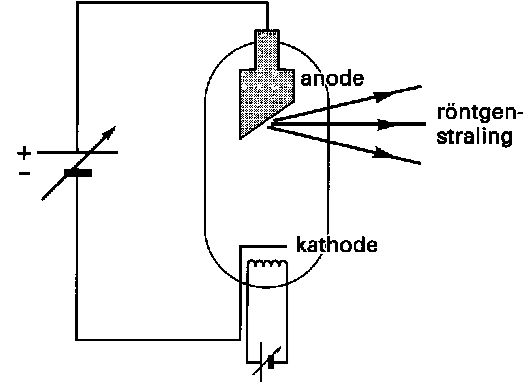
- (4p) De spanning over de kathode en de anode wordt ingesteld op 11 kV. Bereken hiermee de golflengte van de fotonen die vrijkomen en laat zien dat het inderdaad om röntgenfotonen gaat. Ga er hierbij vanuit dat elk elektron al zijn energie gebruikt voor het foton.
- (1p) Leg uit waarom de röntgenbron een groter doordringend vermogen krijgt als de spanning verhoogd wordt.
(Bron: examen HAVO 1999-1)
-
Een onderzoeker wil een calciumion versnellen. Hij doet dit met behulp van een lineaire versneller. Deze versneller bestaat uit een aantal buizen die om en om aan de polen van een wisselspanningsbron verbonden zijn (zie de onderstaande afbeelding). Als gevolg worden de buizen om en om positief en negatief geladen. Binnen in de buizen is het elektrisch veld nul.

- (1p) Leg uit of de lading van de eerste buis positief of negatief moet zijn als het calciumion zich voor de eerste buis bevindt.
- (2p) Leg uit hoe het calciumion tussen de buizen in telkens blijft versnellen.
- (1p) Leg uit waarom de buizen telkens langer moeten worden om het ion te kunnen blijven versnellen.
- (2p) Om het ion nog sterker te versnellen moet de amplitude en de frequentie van de spanningsbron aangepast worden. Leg voor zowel de amplitude als de frequentie uit of deze vergroot of verkleind moeten worden voor een grotere versnelling.
(bron: examen VWO 2005-1)
-
In 1897 ontdekte J. J. Thomson het elektron. Hij ontdekte ook dat het elektron een negatieve lading heeft. Dit deed hij door over een gas zo’n hoge spanning te plaatsen dat er een stroom van elektronen doorheen ging lopen. Hij maakte deze stroom zichtbaar door een gas te kiezen dat oplicht als er elektronen doorheen stromen. Toen plaatste Thomson een condensatorplaat aan weerszijden van de stroom (zie de onderstaande afbeelding. We bekijken de opstelling van bovenaf). Doordat de stroom afboog richting de positieve plaat, wist Thomson dat de elektronen in de stroom negatief moesten zijn.
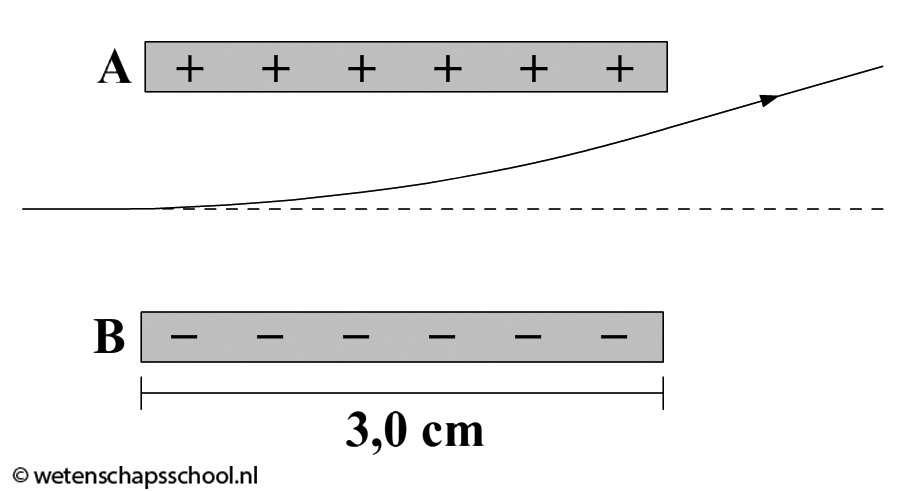
Door de afbuiging nader te bestuderen, lukte het Thomson ook om de verhouding tussen de lading en de massa van het elektron (e/m) te bepalen.
- (4p) Leid af dat de verhouding tussen de lading en de massa van een elektron gelijk is aan:
$$ \frac{e}{m} = \frac{d}{U} a_y $$
U is hier de spanning over de condensatorplaten, ay is de versnelling in de y-richting en d is de afstand tussen de condensatorplaten. Gebruik hiervoor dat de elektrische veldsterkte tussen condensatorplaten gelijk is aan:
$$ E = \frac{U}{d} $$
Je mag de wrijvingskracht en de zwaartekracht verwaarlozen.
-
(5p) De elektronen komen tussen de platen aan met een snelheid van 2,6 × 107 m/s. De lengte van de platen is 3,0 cm, de afstand tussen de platen is gelijk aan 1,2 cm en de spanning over de platen is gelijk aan 410 V. De verplaatsing van de elektronen in de y-richting is gelijk aan Δy = 0,40 cm. Bereken de verhouding tussen de lading en de massa van het elektron. Gebruik hiervoor de volgende formule:
$$ \Delta y = \frac{1}{2}a_y \Delta t^2 $$
|
§2 Magnetisme
De rest van het hoofdstuk zullen we ons focussen op magnetisme. In deze paragraaf bestuderen we het ontstaan van magneetvelden.
Als geladen deeltjes bewegen dan ontstaat er een magneetveld rondom deze deeltjes. De sterkte van dit veld noemen we de magnetische veldsterkte of de magnetische inductie (B). We zien dit bijvoorbeeld gebeuren als we stroom door een draad laten lopen. Er ontstaat dan een magneetveld dat in cirkels om de draad loopt (zie de onderstaande linker afbeelding).
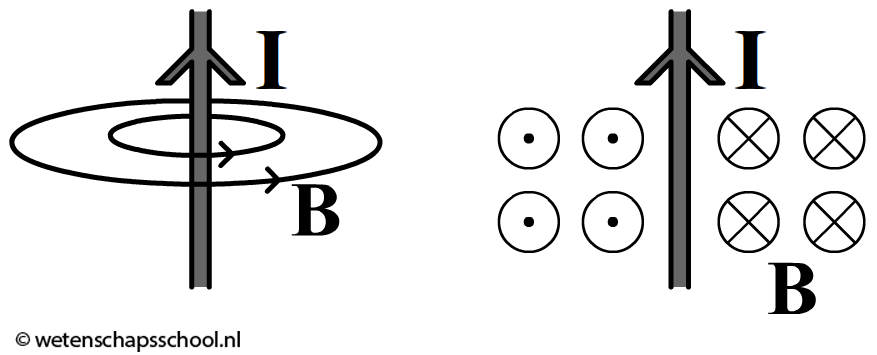
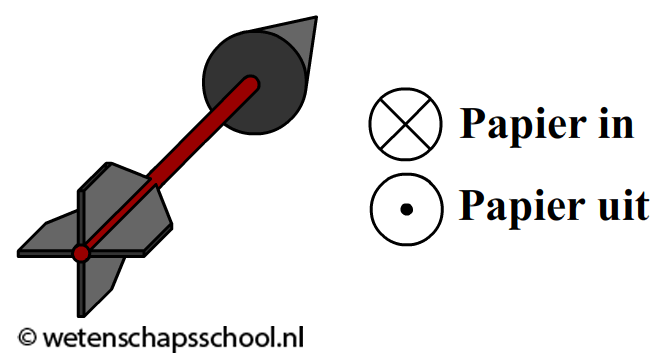
Het is niet altijd even gemakkelijk om in 3D veldlijnen te tekenen. Om dit gemakkelijker te maken, geven we veldlijnen die het papier in gaan weer met een rondje met een kruis erin. Een veldlijn die het papier uit komt geven we weer met een rondje met een stip in het midden (zie de bovenstaande rechter afbeelding). Deze notatie is goed te onthouden door een dartpijl voor te stellen die in de richting van het magneetveld prikt. Gaat de pijl het papier in, dan zien we de achterkant van de pijl—een rondje met een kruisje erin. Komt de pijl het papier uit, dan zien we de voorkant van de pijl—een rondje met een stip in het midden (zie de onderstaande afbeelding).
 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje is dit effect gedemonstreerd. Met behulp van de een raster aan kompasnaaldjes wordt het veld zichtbaar gemaakt.
|
 DEMO-VIDEO:
Magnetische velden
DEMO-VIDEO:
Magnetische velden
|
|
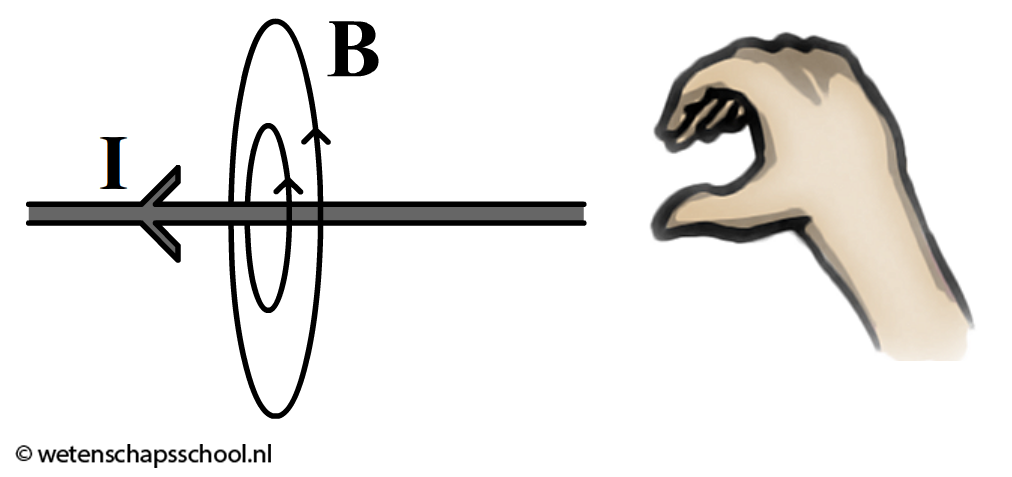
We kunnen de richting van het magneetveld bepalen met behulp van de richting van de stroom (I). De richting van het magneetveld is te vinden door de duim van je rechter hand in de richting van de stroom (I) te wijzen. De vingers van de hand krommen dan automatisch in de richting van het magneetveld (B) (zie de onderstaande afbeeldin). Het is belangrijk te onthouden dat de stroomrichting (I) loopt van de pluspool naar minpool, maar dat de elektronen juist de andere kant op bewegen (van de min naar de plus).
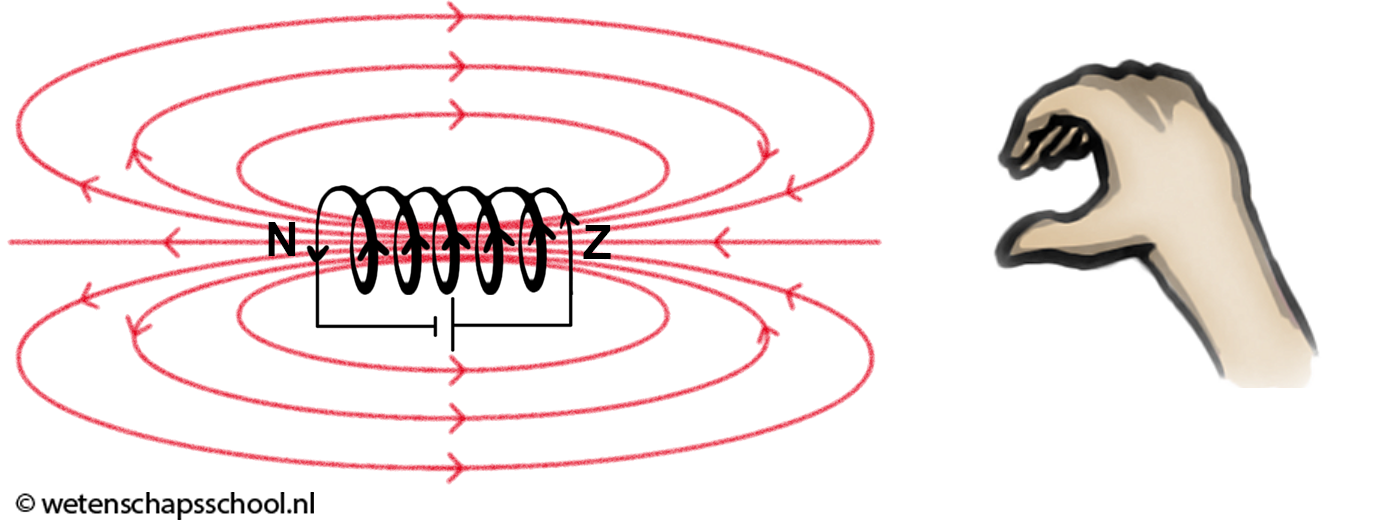
In de onderstaande afbeelding is een stroomdraad een aantal keer omgewonden tot een spoel. Als we stroom laten lopen door een spoel, dan spreken we van een elektromagneet. De richting van het magneetveld in de spoel is te vinden met de rechter hand. Als je de vingers van je hand in de richting van de stroom (I) kromt, dan wijst je duim in de richting van het magneetveld (B) in de spoel. Merk op dat het magneetveld buiten de spoel precies de andere kant op wijst. De plek waar de magneetveldlijnen uit de spoel komen noemen we de noordpool van de elektromagneet. De kant waar de veldlijnen naar binnen komen noemen we de zuidpool.
Een handige eigenschap van een elektromagneet is dat we deze aan en uit kunnen zetten door simpelweg de stroomkring te sluiten of te openen. Dit kan bijvoorbeeld handig zijn bij het sorteren van ijzeren voorwerpen in een berg afval (zie de onderstaande afbeelding). IJzer en nikkel hebben de eigenschap dat het wordt aangetrokken tot zowel de noord- als de zuidpool van een magneet. Als de elektromagneet aan staat, dan trekt het stukken ijzer aan. Als de stroom uitgezet wordt, dan vallen de stukken ijzer er weer vanaf.
 (Afbeelding: Marjory Collins; Library of Congress; PD)
(Afbeelding: Marjory Collins; Library of Congress; PD)
Naast elektromagneten bestaan er ook permanente magneten. In de afbeelding hieronder zijn wat stukjes ijzer rond een permanente magneet neergestrooid. Als kleine kompasnaaldjes gaan deze stukjes ijzer in de richting van het magnetische veld wijzen. Merk op dat het magnetische veld precies dezelfde vorm heeft als bij de elektromagneet. Net als bij de spoel wordt dit veld veroorzaakt door bewegende elektronen. In dit geval de elektronen die rondbewegen in de atomen waaruit de permanente magneet bestaat.
 (Afbeelding: Boyce Duprey; CC BY 2.0)
(Afbeelding: Boyce Duprey; CC BY 2.0)
Een magneet kan worden gemaakt door een stuk ijzer op te warmen en in een extern magneetveld te leggen. Dit magneetveld zorgt ervoor dat de elektronen allemaal in dezelfde richting gaan roteren. De optelling van de magneetvelden van al deze elektronen tezamen vormt het magneetveld van een permanente magneet. Als we de magneet nogmaals opwarmen, maar dan zonder extern magneetveld, dan trillen de elektronen in willekeurige richting en heffen de magneetvelden elkaar op. Als gevolg hiervan verdwijnen de magnetische eigenschappen.
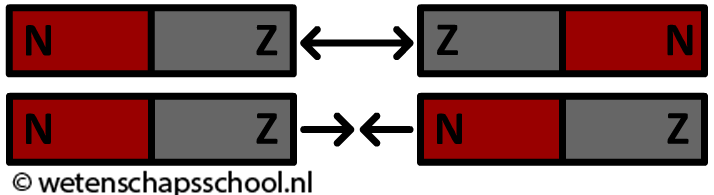
Voor zowel permanente magneten als elektromagneten geldt dat gelijke polen elkaar afstoten en verschillende polen elkaar aantrekken:
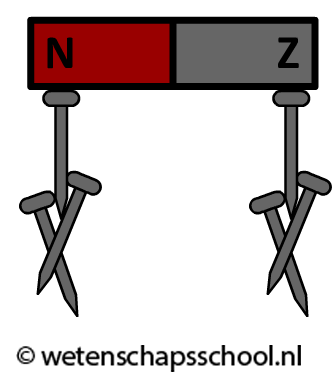
Wanneer je een ijzeren spijker in de buurt van een magneet houdt, wordt deze spijker ook magnetisch. Als gevolg wordt de spijker door de magneet aangetrokken. Deze spijker kan dan weer een volgende spijker aantrekken (zie de afbeelding linksonder). We noemen dit proces magnetische influentie. Als de spijker weer weg wordt gehaald bij de magneet, dan verdwijnen de magnetische eigenschappen weer.
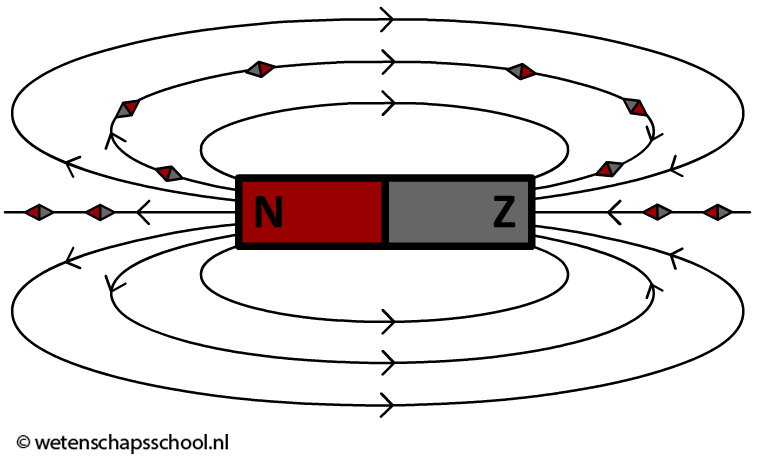
Een bekende toepassing van magnetisme is het kompas. Een kompas is niets anders dan een klein magneetje dat een kracht ondervindt van het aardmagnetisch veld. De noordpool van een kompas wijst in de richting van het magneetveld en de zuidpool tegen de richting van het magneetveld in. In de onderstaande rechter afbeelding zien we hoe kompasjes reageren op het veld van een permanente magneet.
 INSTRUCTIE:
Magnetische velden
INSTRUCTIE:
Magnetische velden
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je het magneetveld om een stroomvoerende draad kan schetsen met behulp van de rechterhandregel.
- Zorg dat je een magneetveld dat het papier in prikt aangeeft met een rondje met een kruis erin en een magneetveld dat het papier uit prikt met een rondje met een stip erin.
- Zorg dat je het magnetisch veld om een spoel of elektromagneet kan schetsen met behulp van de rechterhandregel. Zorg ook dat je weet dat de veldlijnen bij de noordpool de spoel uitkomen en bij de zuidpool de spoel inkomen.
- Zorg dat je weet dat gelijke polen van permanente magneten of elektromagneten elkaar afstoten en dat verschillende polen elkaar aantrekken. IJzer en nikkel worden aangetrokken door zowel de noord- als de zuidpool van magneten.
- Zorg dat je weet dat ijzervijlsel en kompassen in de richting van magnetische veldlijnen wijzen.
|
 Opdrachten
Opdrachten
|
-
(2p) Beschrijf de rechterhandregel voor een rechte stroomvoerende draad en de rechterhandregel voor een spoel.
-
In de onderstaande afbeelding is een stroomkring afgebeeld:
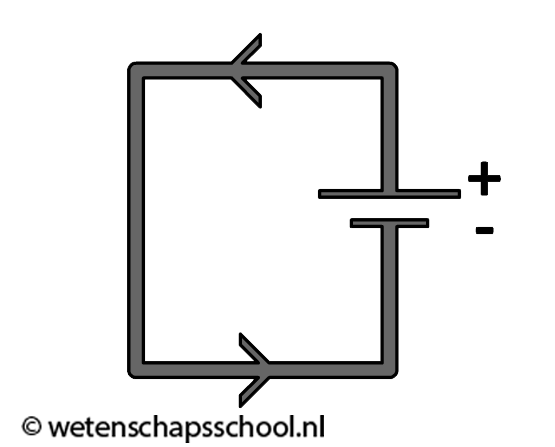
- (2p) Leg uit of de pijlen in de afbeelding de stroomrichting aangeven of de richting van de elektronenstroom.
- (2p) Teken het magneetveld van de linker draad in de schakeling.
-
(2p) Schets het magneetveld in elk van de twee onderste afbeeldingen:

-
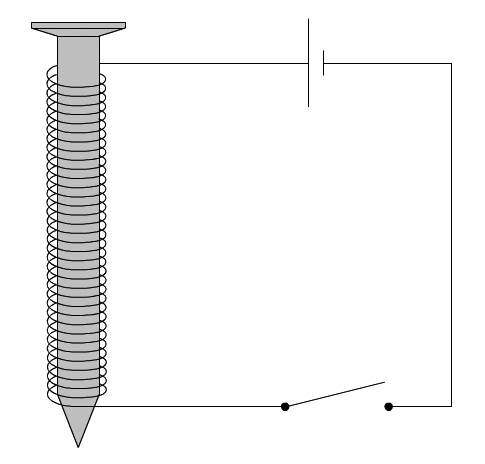
(3p) Een spijker wordt magnetisch gemaakt door er een draad omheen te wikkelen en hier stroom doorheen te laten lopen (zie de onderstaande afbeelding). Schets het magneetveld van de spoel en geef met de letters N en Z aan waar de noord- en zuidpool van de spijker zich bevinden.
-
In de onderstaande afbeelding zien we een schakeling van een schoolbel die continu blijft rinkelen zolang de schakelaar ingedrukt blijft. Bij punt A is een contactje afgebeeld dat in de afbeelding de klepel raakt. Het contactje zit echter niet vast aan de klepel.
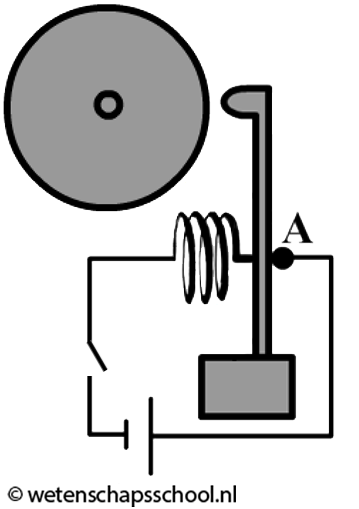
- (3p) Beschrijf de werking van de schoolbel.
- (1p) Maakt het voor de werking van de bel uit hoe om de spoel gewikkeld is?
- (2p) Met een kompas kunnen we de richting van het aardmagnetisch veld vinden. Maak een schets van het magneetveld van de aarde en teken een kompas bij de evenaar. Geef ook met de letters N en Z de noord- en de zuidpool aan van zowel de aarde als de magneet. Merk je iets vreemds op bij het tekenen van de noord en zuidpool van de aarde?
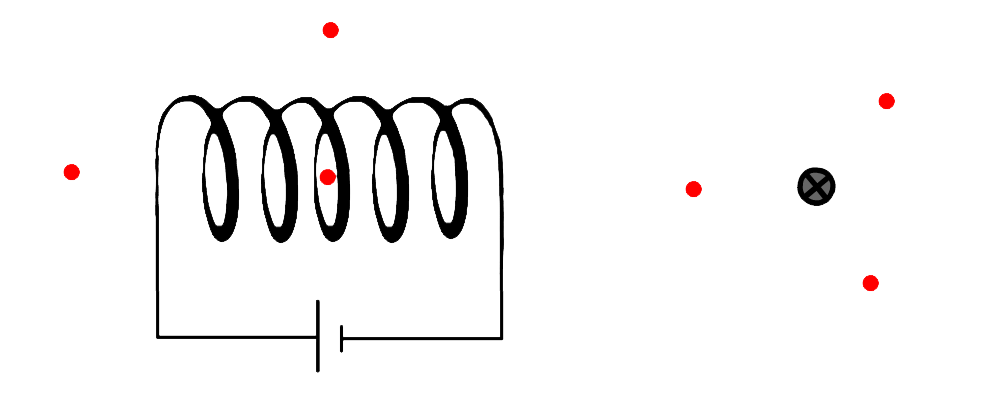
- (4p) In de onderstaande afbeelding zien we aan de linkerkant een spoel en aan de rechterkant een draad waarbij de stroomrichting het papier in loopt.
Ook zien we in beide afbeelding drie stippen. Teken bij al deze stippen een kompas.
Geef duidelijk de richting van het kompas aan en aan welke kant de noord- en de zuidpool zich bevindt.
|
§3 De lorentzkracht
In deze paragraaf bestuderen we de kracht die een magneetveld op een bewegende lading kan uitoefenen. We noemen dit de lorentzkracht. Aan het eind van de paragraaf gaan we zien hoe we met behulp van deze kracht een elektromotor kunnen maken.
In de vorige paragraaf hebben we gelezen dat bewegende lading zorgt voor een magneetveld. Een magneetveld kan op zijn beurt een kracht uitoefenen op andere bewegende ladingen. Deze kracht wordt de lorentzkracht (FL) genoemd. De grootte van de lorentzkracht werkende op een stroomdraad kan als volgt worden berekend:
$$ F_L = BIL $$
|
Lorentzkracht (FL)
|
newton (N)
|
|
Magnetische veldsterkte / inductie (B)
|
tesla (T)
|
|
Stroomsterkte (I)
|
ampère (A)
|
|
Lengte van de stroomdraad (L)
|
meter (m)
|
|
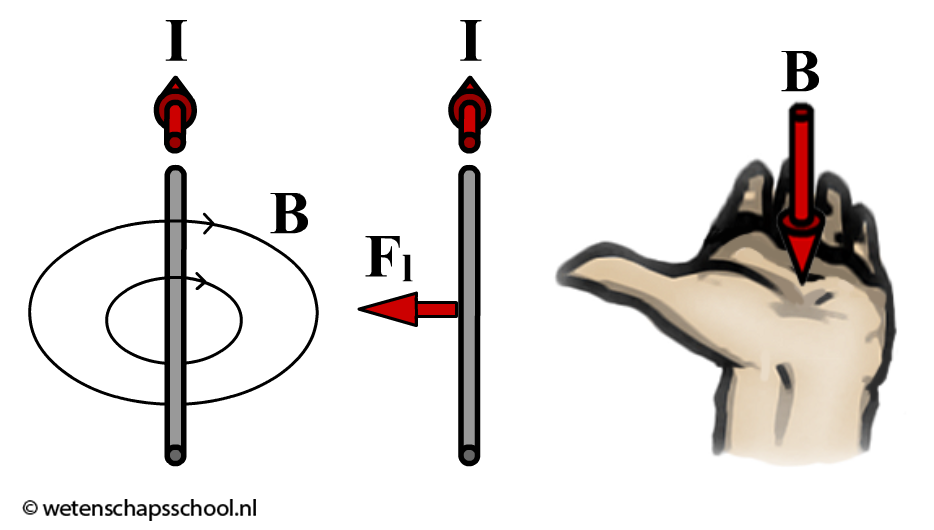
Hieronder zien we bijvoorbeeld twee stroomdraden. Met de rechterhandregel uit de vorige paragraaf vinden we dat het magneetveld om de linker draad kromt zoals hieronder is aangegeven. Dit magneetveld van de linker draad valt op de rechterdraad en oefent hier een lorentzkracht uit. Als je je vingers van je linkerhand in de richting van de stroom (I) laat wijzen en het magneetveld (B) in je palm laat prikken, dan wijst je duim in de richting van de lorentzkracht (FL). In deze afbeelding werkt de lorentzkracht op de rechter draad dus naar links. Hetzelfde kunnen we doen voor de kracht die het magneetveld van de rechter draad op de linker draad uitoefent. Als gevolg vinden we dat de draden naar elkaar toe worden getrokken.
 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje wordt dit effect zichtbaar. Twee parallelle draden waardoor stroom in dezelfde richting loopt trekken elkaar aan. Twee draden waarbij de stroom in tegengestelde richting loopt, stoten elkaar juist af.
|
 DEMO-VIDEO:
Lorentzkracht
DEMO-VIDEO:
Lorentzkracht
|
|
De lorentzkracht werkende op een enkel geladen deeltje dat beweegt met snelheid v kunnen we als volgt berekenen:
$$ F_L = Bqv $$
|
Lorentzkracht (FL)
|
newton (N)
|
|
Magnetische veldsterkte / magnetische inductie
|
tesla (T)
|
|
Lading (q)
|
coulomb (C)
|
|
Snelheid (v)
|
meter per seconde (m/s)
|
|
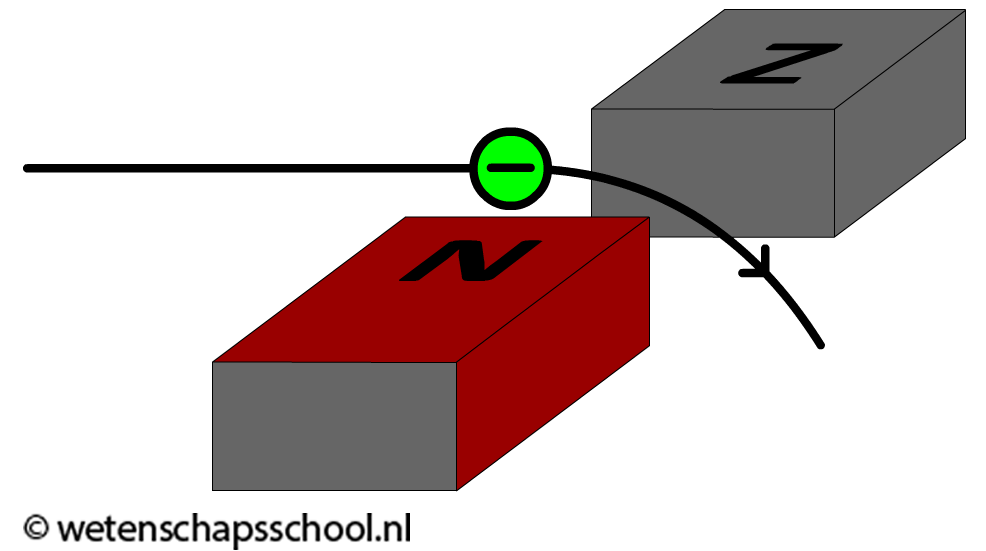
In de onderstaande afbeelding zien we een elektron dat naar rechts beweegt door een extern magneetveld. De veldlijnen van het magneetveld lopen van noord naar zuid. Ze gaan in deze afbeelding dus het papier in. Let erop dat de richting van de stroom tegen de beweging van het elektron in gaat. Met de linkerhandregel vinden we nu dat de lorentzkracht naar beneden wijst (ga dit na!). Als gevolg buigt het elektron naar beneden af.
 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje zien we dit effect:
|
 DEMO-VIDEO:
Elektronenbundel
DEMO-VIDEO:
Elektronenbundel
|
|
Wat zou er gebeuren als we een positieve lading door dit magneetveld schieten? Bij een positieve lading wijst de stroom (I) wel in de bewegingsrichting van de deeltjes en als gevolg zal de lorentzkracht naar boven wijzen (ga dit zelf na met de linkerhandregel). De positieve lading zou dan omhoog afbuigen. Neutrale deeltjes trekken zich niks aan van het magneetveld en gaan gewoon rechtdoor.
Als je een geladen deeltje een magneetveld in schiet, dan zorgt de lorentzkracht ervoor dat dit deeltje een cirkelbaan gaat uitvoeren. Bij een cirkelbaan kunnen we de lorentzkracht gelijk stellen aan de middelpuntzoekende kracht:
$$ F_L = F_{mpz} $$
Als we de formules voor de lorentzkracht en de middelpuntzoekende kracht invullen, dan vinden we:
$$ Bqv = \frac{mv^2}{r} $$
Door deze formule om te schrijven kunnen we bijvoorbeeld de massa van geladen deeltjes bepalen:
$$ m = \frac{Bqr}{v} $$
 INSTRUCTIE:
De lorentzkracht
INSTRUCTIE:
De lorentzkracht
 INSTRUCTIE:
Elektronenbundel
INSTRUCTIE:
Elektronenbundel
De belangrijkste toepassing van de lorentzkracht is de elektromotor. Een elektromotor zet elektrische energie om in kinetische energie.
 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje zien we een simpele vorm van een elektromotor. De stroom loopt hier door de magneet en zorgt voor een lorentzkracht die de magneet laat draaien.
|
 DEMO-VIDEO:
De elektromotor
DEMO-VIDEO:
De elektromotor
|
|
Hieronder zien we een meer stabiele elektromotor. Het magneetveld in de afbeelding zorgt ervoor dat er lorentzkrachten gaan werken op het stroomlusje tussen de magneten. Deze krachten roteren de lus, totdat het in een verticale positie komt te staan. Om het draad nu verder te laten roteren is het nodig dat de krachten omdraaien. Dit gebeurt in deze opstelling automatisch, doordat vanaf dit moment de stroomrichting in de draad omdraait. Dit gebeurt dankzij de collector. Dit is een cilindervormig onderdeel dat bestaat uit twee geleidende halve schijven, met daartussen een stukje isolerend materiaal. In de bovenstaande afbeelding is het ene deel van de collector verbonden met de plus en het andere deel met de min. Als de collector genoeg draait, draait de stroomrichting in de lus om en als gevolg ook de lorentzkracht. Op deze manier blijft het lusje draaien. In de animatie op de website is dit proces beter te zien. (zie de onderstaande animatie).
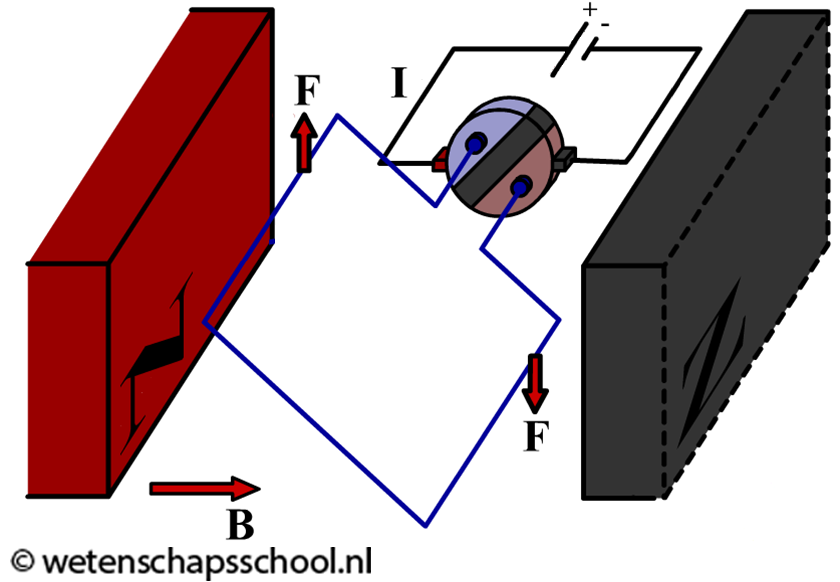
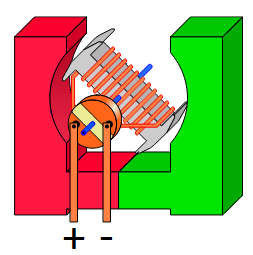
Je kan deze elektromotor een stuk krachtiger maken door in plaats van één stroomlusje een hele spoel tussen de permanente magneten te plaatsen. De lorentzkracht werkt dan op elke winding van de spoel, waardoor de resulterende kracht veel groter wordt.
 INSTRUCTIE:
De elektromotor
INSTRUCTIE:
De elektromotor
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je kan rekenen met de lorentzkracht met behulp van de formules "FL = BIl" en "FL = Bqv". De eerste formule gebruik je bij een stroomvoerende draad en de tweede bij een bewegende lading.
- Zorg dat je weet dat de lorentzkracht ontstaat als geladen deeltjes door een magneetveld bewegen. Zorg ook dat je met de linkerhandregel de richting van de lorentzkracht kan bepalen.
- Zorg dat je weet dat de stroomrichting in de bewegingsrichting wijst van positieve ladingen en tegen de bewegingsrichting van negatieve ladingen.
- Zorg dat je weet dat geladen deeltjes in een magneetveld cirkelbanen maken dankzij de lorentzkracht. In deze gevallen kan je de lorentzkracht gelijkstellen aan de middelpuntzoekende kracht.
- Zorg dat je de werking van de elektromotor begrijpt. Snap o.a. waarom de collector nodig is om elke halve rotatie de stroom van richting om te draaien.
|
 Opdrachten
Opdrachten
|
- (1p) Beschrijf het gebruik van de linkerhandregel.
- (4p) Teken in de onderstaande afbeeldingen de richting van het magneetveld om beide draden en de richting van de lorentzkracht werkende op de draden. De pijlen in de afbeelding geven de stroomrichting aan.
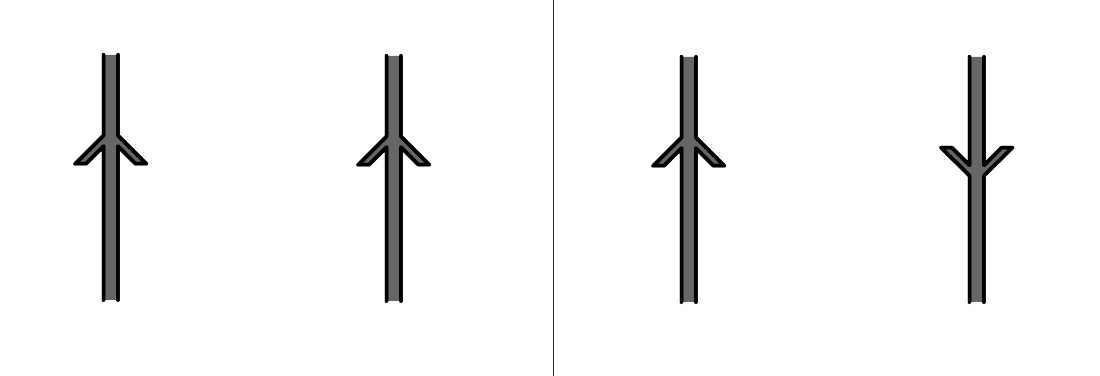
- Een leerling maakt de volgende schakeling van een zestal dezelfde draden (zie de linker onderstaande afbeelding). De ampèremeter geeft 25 A aan. In de rechter afbeelding is ingezoomd op draad 2, 3 en 4:
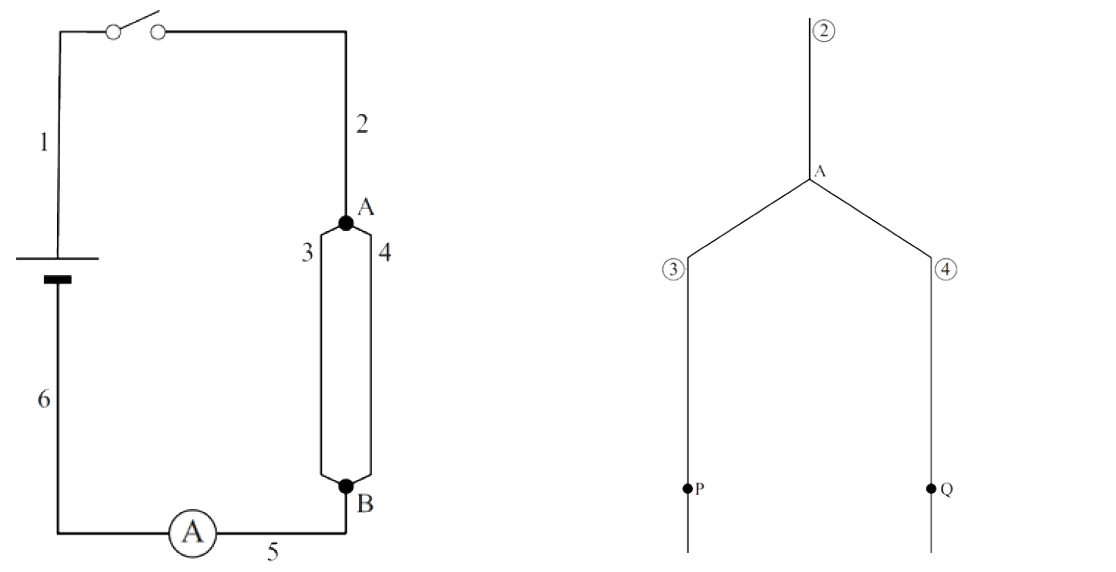
- (3p) Bepaal in welke richting de lorentzkracht werkt op punt Q. Teken hiervoor ook het relevante magneetveld en geef aan in welke richting de stroom loopt.
- (4p) De sterkte van het magneetveld om een draad wordt gegeven door:
$$ B = \frac{\mu_0I}{2\pi r} $$
μ0 is de magnetische permeabiliteit en is te vinden in BINAS tabel 7. r is de afstand tot de draad in meter. De draden 3 en 4 bevinden zich op een afstand van 4,0 cm van elkaar en hebben een lengte van 50 cm. Bereken de grootte van de lorentzkracht op draad 4.
(bron: examen VWO 2013-2)
-
Bij verval van Seleen-82 komen twee elektronen vrij (ook wel β--deeltjes genoemd). Dit weten we door het seleenatoom in een sterk extern magneetveld te plaatsten. De elektronen maken dan de baan die in de afbeelding geschetst is.
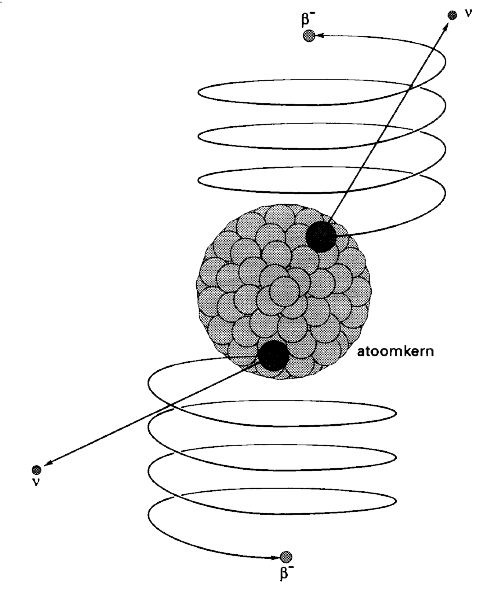
- (3p) In welke richting loopt het externe magneetveld. Licht je antwoord toe.
- (2p) Leg uit hoe het pad van een positron eruit had gezien.
(bron: examen VWO 1993-1)
- Permanente magneten en elektromagneten werken dankzij hetzelfde principe, namelijk door de vorming van magneetvelden om stromende lading.
- (1p) Wat zorgt er in een permanente magneet voor stromende lading?
- (2p) Als je een permanente magneet warm maakt, dan verdwijnen de magnetische eigenschappen. Verklaar dit.
-
In de onderstaande afbeelding zien we een schakeling bestaande uit twee metalen balkjes en een metalen cilinder die vrij kan bewegen over deze balkjes (de afbeelding is van boven af weergegeven). Tussen punt P en Q wordt een batterij aangesloten die een stroomsterkte van 1,2 A levert. We laten een magneetveld met een magnetische inductie van 0,10 T van boven naar beneden op de schakeling vallen. De balkjes zijn 20 cm lang en de afstand tussen de balkjes is 10 cm.
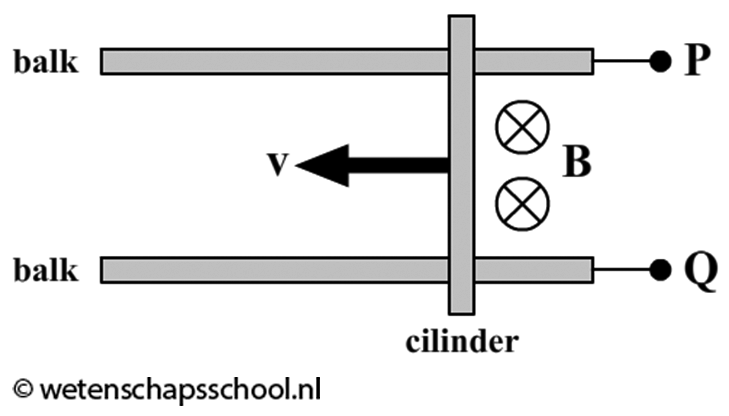
- (2p) Als de stroomkring gesloten wordt, begint de cilinder naar links te bewegen. Geef de richting van de stroom. Licht je antwoord toe.
- (3p) Bereken de lorentzkracht die op de cilinder werkt.
-
In de onderstaande afbeelding zien we de sporen van deeltjes in een zogenaamd bubbelvat. Deeltjes laten in dit vat een spoor van bubbeltjes achter die gefotografeerd kunnen worden. Over het vat staat ook een extern magnetisch veld. Dit veld zorgt ervoor dat er een lorentzkracht gaat werken op de geladen deeltjes. In het onderstaande voorbeeld zien we een foton (een lichtdeeltje) dat plotseling verandert in een elektron en een positron. De afbeelding is op ware grootte weergegeven.
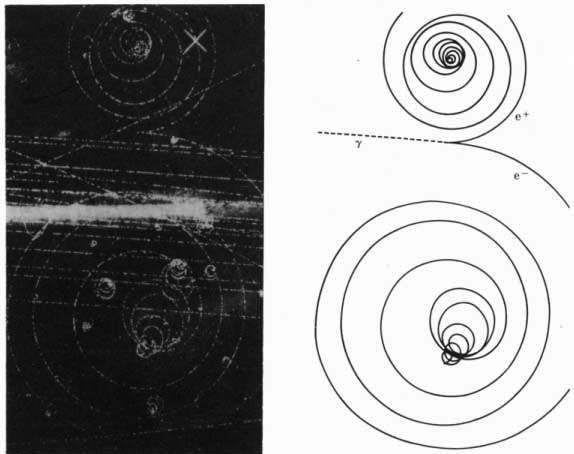
- (3p) Bepaal met behulp van de afbeelding de richting van het magneetveld.
- (5p) Nadat de deeltjes ontstaan, beginnen ze aan een cirkelbaan in het magneetveld. Door de wrijvingskracht die de deeltjes ondervinden spiraliseren ze naar binnen. In het eerste deel van de beweging heeft de wrijvingskracht echter nog weinig invloed gehad op de beweging. Bepaal met behulp van de afbeelding de oorspronkelijke snelheid van het elektron. De magnetische inductie van het externe magneetveld is 0,011 T.
-
Je haalt een ventilator uit elkaar en vindt de schakeling die hieronder schematisch getekend is:
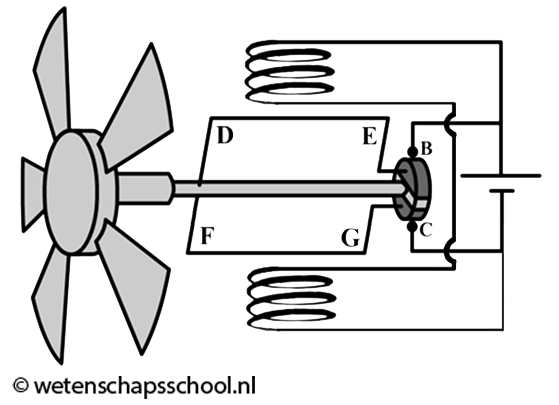
- (2p) Wat is de richting van het magneetveld tussen de twee spoelen in?
- (2p) Wat zijn de richtingen van de kracht op het draadstuk DE en FG?
- (1p) In de afbeelding is een cilindervormig apparaat afgebeeld genaamd een commutator (ook wel een collector genoemd). Waarom is het cilindervormige apparaat nodig om de ventilator in beweging te laten blijven?
- (4p) Werkt de ventilator ook als we de gelijkspanningsbron vervangen door een wisselspanningsbron. Leg je antwoord uit.
- (3p) In werkelijkheid wordt de enkele winding DEFG vervangen door een spoel met N windingen. Dit zorgt ervoor dat op zijde DE en FG van de spoel elk een lorentzkracht van 15 N wordt uitgeoefend, genoeg om de ventilator te laten draaien. De magnetische inductie is gelijk aan 10 T, draadstukken DE en FG zijn elk 3,0 cm lang en de stroomsterkte is 200 mA. Bereken het aantal windingen dat gebruikt is.
-
Lood in ertsen uit mijnen bestaat voornamelijk uit de isotopen lood-206, lood-207 en lood-208. Om na te gaan of een bepaalde isotoop in een stofmengsel aanwezig is, kan een massaspectrometer gebruikt worden. Hieronder is een massaspectrometer schematisch weergegeven:
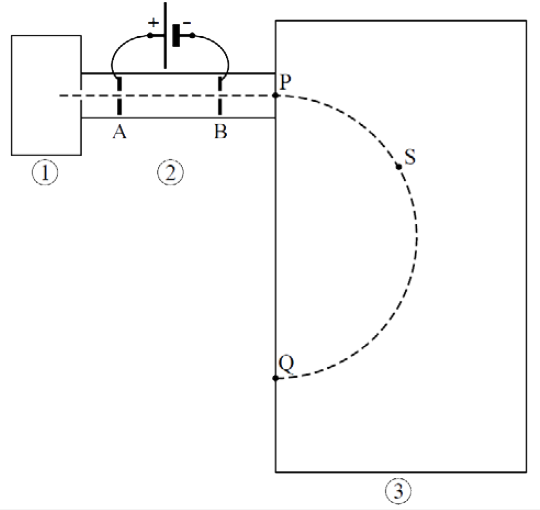
Het stofmengsel wordt eerst gasvormig gemaakt en daarna onder lage druk in de ionisatieruimte (1) gebracht. De geïoniseerde moleculen of atomen komen vervolgens in een vacuümruimte (2). Hierin worden ze door een elektrisch veld versneld. In ruimte 3 worden ze door een magnetisch veld afgebogen en ten slotte in punt Q gedetecteerd. Een mengsel met éénwaardige positieve ionen van lood-206, lood-207 en lood-208 komt met een te verwaarlozen beginsnelheid in ruimte 2.
- (4p) Beredeneer welke van de drie isotopen in P de grootste snelheid heeft.
- (3p) Vervolgens worden de deeltjes afgebogen door het magnetisch veld. De ionen doorlopen een halve cirkelbaan. Bepaal de richting van het magnetisch veld in ruimte 3. Geef daartoe eerst in punt S de richtingen aan van de snelheid en de lorentzkracht.
- (5p) In punt Q worden de ionen gedetecteerd. Uit de sterkte van het magnetisch veld (B) en de versnelspanning (UAB) kan worden afgeleid om welke isotoop het gaat. De massa van een isotoop kan worden berekend met de volgende formule:
$$ m = \frac{B^2qr^2}{2U_{AB}} $$
Leid deze formule af met behulp van formules uit BINAS.
- (3p) De sterkte van het magnetisch veld wordt ingesteld op 0,182 T. De afstand PQ bedraagt 56,0 cm. Bereken de versnelspanning waarbij lood-207-ionen in de detector in punt Q terechtkomen.
(bron: examen VWO 2010-1)
- (8p) Een Ca2+-ion met een massagetal van 48 wordt vanuit stilstand versnelt tussen twee geladen platen waarover een spanningsverschil van 2,40 kV staat. Het versnelde ion komt dan in een extern magneetveld terecht. Het ion maakt in dit magneetveld een halve cirkelbaan met een diameter van 52,6 cm. Bereken de grootte van de magnetische inductie van dit externe veld.
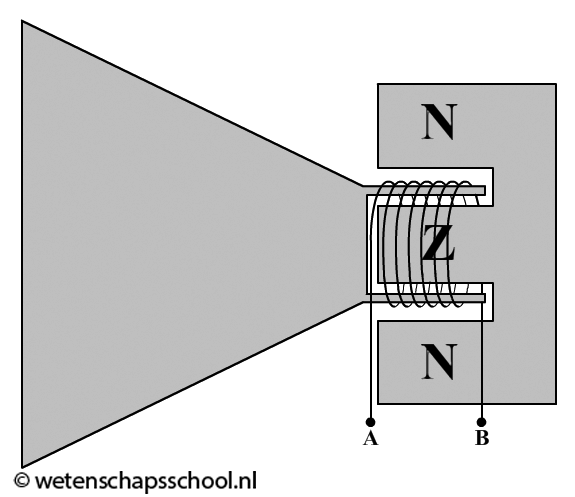
- (4p) Een leerling maakt zelf een simpele luidspreker. De luidspreker bestaat uit een papieren conus die heen en weer kan bewegen om geluidsgolven te produceren. Aan de conus is een spoel bevestigd en deze wordt over de zuidpool van een permanente magneet geschoven (zie de onderstaande afbeelding). Leg uit in welke richting de stroom moet stromen om de conus in te schuiven.
-
(LASTIG, MAAR INZICHTELIJK) In de onderstaande afbeelding zijn twee keer twee stroomkringen weergegeven, die zich boven elkaar bevinden:
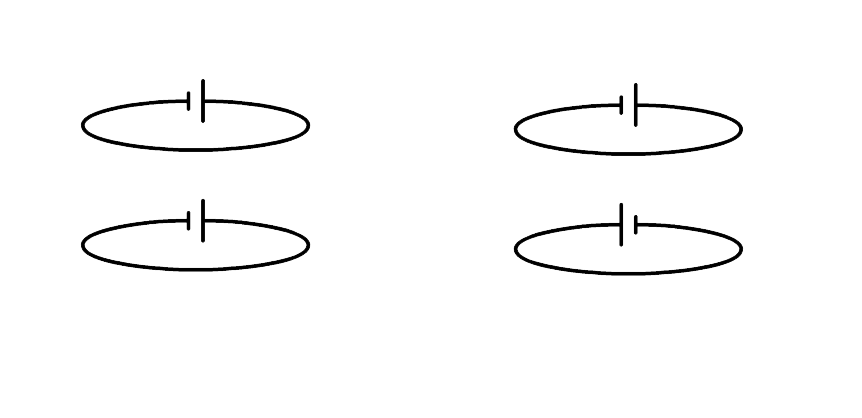
- (4p) Teken de magneetvelden die de stroomkringen genereren en de lorentzkrachten die deze magneetvelden tot gevolg hebben. Schrijf ook bij elke stroomkring waar de noord- en zuidpool zich bevinden.
- (1p) In de vorige vraag zien we waarom elektromagneten elkaar afstoten of aantrekken. Dit komt door de lorentzkracht. Permanente magneten werken op een soortgelijke manier. Leg uit welke stroom hier zorgt voor de lorentzkracht.
- (2p) Als je een permanente magneet warm maakt, dan verdwijnen de magnetische eigenschappen. Verklaar dit.
|
§4 Inductie
In de vorige paragraaf hebben we gezien hoe we met een stroom en een magneetveld een kracht kunnen opwekken. In deze paragraaf gaan we zien dat we met een veranderend magneetveld een stroom kunnen opwekken. We noemen dit inductie.
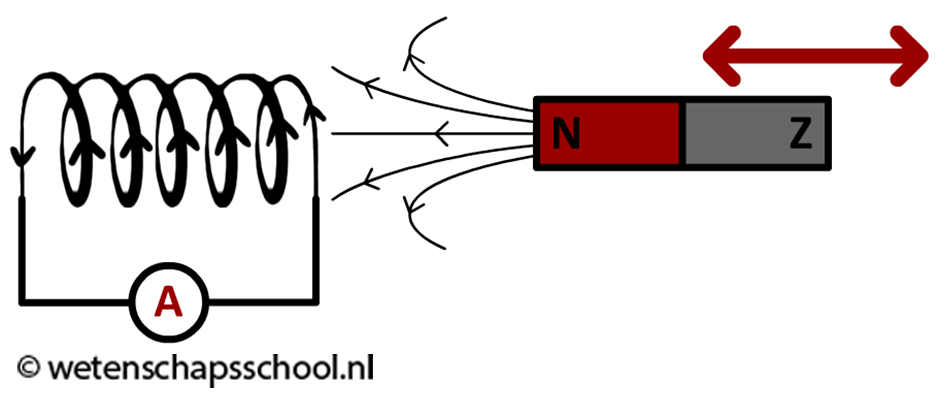
Eerder in dit hoofdstuk hebben we gelezen dat bewegende ladingen zorgen voor een magneetveld. In deze paragraaf gaan we het omgekeerde proces bestuderen: een veranderend magneetveld kan ervoor zorgen dat ladingen gaan bewegen. We kunnen dit bijvoorbeeld zien als we een magneet bewegen in de buurt van een spoel die is opgenomen in een gesloten stroomkring. Door het bewegen van de magneet gaat er een stroom lopen door de schakeling. Op deze manier kunnen we kinetische energie omzetten in elektrische energie. We noemen dit effect inductie.
 Demonstratievideo
Demonstratievideo
|
|
In de rechter video is dit effect te zien. Twee tegengesteld gerichte LED-lampen zijn aangesloten op de spoel. Zo is te zien dat de stroomrichting afhangt van of we de magneet richting de spoel of juist van de spoel af bewegen (later in dit hoofdstuk gaan we hier preciezer naar kijken).
|
 DEMO-VIDEO:
Inductie
DEMO-VIDEO:
Inductie
|
|
Inductie vindt o.a. plaats in een dynamo. De beweging van het wiel van je fiets zorgt voor de beweging van magneten in de dynamo. Deze bewegende magneten zorgen er weer voor dat er een stroom gaat lopen door een spoel en hiermee gaat je lamp branden. Ook energiecentrales werken op deze manier. In bijvoorbeeld een waterkrachtcentrale zorgt water ervoor dat een turbine gaat roteren. In een zogenaamde generator worden hiermee spoelen geroteerd binnen een magnetisch veld. Als gevolg gaat er in de spoel een stroom lopen (zie het hoofdstuk "Energie").
Om de grootte van de inductiespanning te kunnen bepalen, moeten we eerst het begrip flux (φ) begrijpen. De flux is een maat voor de hoeveelheid magnetische veldlijnen die door een oppervlak (A) steekt. Neem bijvoorbeeld een stroomdraad in de vorm van een vierkant (zie de linker onderstaande afbeelding). In de rechter drie afbeeldingen zien we deze draad van de zijkant in een extern magnetisch veld. Door de draad te kantelen kunnen we meer of minder veldlijnen door dit oppervlak laten prikken. De rode veldlijnen prikken door het stroomlusje heen en de zwarte lijnen niet. Hoe minder veldlijnen er door dit oppervlak prikken, hoe kleiner de flux. In de meest rechtse afbeelding is de flux zelfs nul.

De grootte van de flux kunnen we met de volgende formule berekenen:
$$ \phi = B_\perp A $$
|
Flux (φ)
|
weber (Wb)
|
|
Loodrechte component van de magnetische veldsterkte /
inductie (B⊥)
|
tesla (T)
|
|
Oppervlak (A)
|
vierkante meter (m2)
|
|
B⊥ staat voor de component van de magnetische inductie in de richting loodrecht op het oppervlak (zie de onderstaande afbeelding).
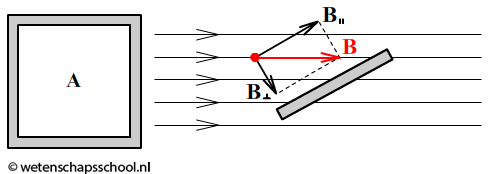
Een verandering van de flux in de tijd zorgt dat er een spanning (U) ontstaat. We noemen dit de inductiespanning (Uind). De grootte van deze spanning kunnen we als volgt berekenen:
$$ U_{ind} = -N \frac{d\phi}{dt} $$
|
Inductiespanning (Uind)
|
volt (V)
|
|
Flux (φ)
|
weber (Wb)
|
|
Tijd (t)
|
seconde (s)
|
|
Aantal windingen (N)
|
windingen
|
|
In ons vierkante stroomlusje was het aantal windingen (N) gelijk aan 1, maar deze formule kan ook gebruikt worden voor een spoel met N windingen. dφ/dt is de afgeleide van de flux naar de tijd. Er geldt dus dat hoe sneller de flux verandert, hoe groter de inductiespanning wordt. Als de flux constant is, dan wordt deze afgeleide nul en is er dus geen spanning.
Er zijn een aantal manieren om de flux te veranderen. We hebben hierboven bijvoorbeeld gezien dat dit kan door de stroomkring te roteren in een magneetveld. Een andere manier is door een stroomkring in en uit een magneetveld te bewegen (zie de eerste onderstaande afbeelding) of door het magneetveld in en uit een stroomkring te bewegen (zie de tweede afbeelding). In de derde afbeelding ontstaat geen inductiespanning. Hoewel de stroomkring beweegt in het magneetveld, blijft het aantal veldlijnen dat door de stroomkring prikt gelijk en als gevolg hebben we geen fluxverandering en dus ook geen inductiespanning.

 Demonstratievideo
Demonstratievideo
|
|
In het rechter filmpje wordt dit effect gedemonstreerd. In de tweede helft van het filmpje wordt ook een weekijzeren kern in de spoel gelegd. Dit ijzer wordt door het magneetveld van de spoel gemagnetiseerd, waardoor het veld sterker wordt.
|
|
|
Een andere belangrijke toepassing van inductie is de transformator. In de onderstaande afbeelding is te zien dat een transformator uit twee schakelingen bestaat. De linker schakeling bestaat uit een wisselspanningsbron en een spoel. De wisselspanning zorgt voor een veranderend magneetveld in de spoel. Dit veranderend magneetveld zorgt voor een fluxverandering in de spoel in de rechter schakeling en als gevolg gaat hier een inductiestroom lopen.
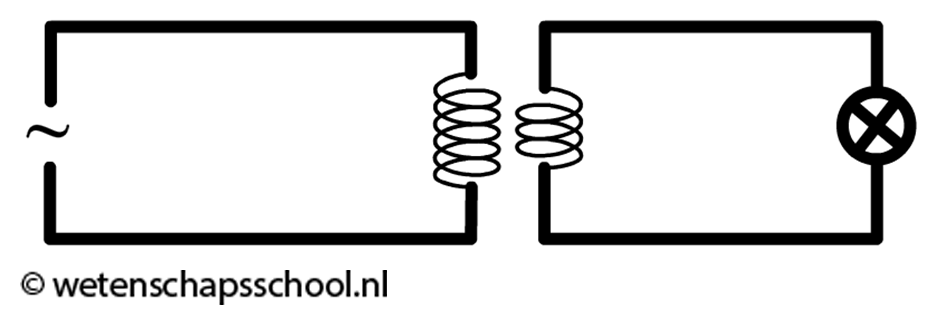
De transformator heeft een aantal nuttige toepassingen. Een transformator kan bijvoorbeeld gebruikt worden om elektrische tandenborstels op te laden zonder dat er bedrading loopt van de oplader naar de tandenborstel. Als gevolg kunnen we de tandenborstel veilig gebruiken in de badkamer zonder het risico dat er kortsluiting ontstaat.

Een transformator kan ook gebruikt worden om de spanning omhoog of omlaag te transformeren. Over een stopcontact staat bijvoorbeeld altijd een spanning van 230 V. Dit is voor veel apparaten echter veel te hoog. Laptops werken bijvoorbeeld op zo'n 20 V. Door een goede verhouding te kiezen tussen de windingen van de twee spoelen kan de spanning omhoog of omlaag getransformeerd worden.
 INSTRUCTIE:
Flux
INSTRUCTIE:
Flux
 INSTRUCTIE:
Inductie
INSTRUCTIE:
Inductie
 Leerdoelen:
Leerdoelen:
|
- Zorg dat je weet dat het bewegen van een magneet in de buurt van een spoel (of het bewegen van een spoel in de buurt van een magneet) ervoor zorgt dat er spanning wordt opgewekt in de spoel. We noemen dit inductiespanning. Bij een generator en een dynamo wordt op deze manier elektriciteit opgewekt.
- Zorg dat je kan rekenen met de flux met behulp van de formule "φ = B⊥A", waarbij "B⊥" de component van het magneetveld is die door de stroomkring wijst.
- Zorg dat je weet dat fluxverandering door een stroomkring zorgt voor een inductiespanning. Zorg dat je hiermee kan rekenen met behulp van de formule "Uind = -Ndφ/dt", waarbij "N" het aantal windingen van de stroomkring is en "dφ/dt" de verandering van de flux in de tijd.
- Zorg dat je weet dat je "dφ/dt" kan bepalen met behulp van een raaklijn in een (φ,t)-diagram (zie de opdrachten) en zorg dat je weet dat bij constante flux de inductiespanning nul is.
- Zorg dat je de werking van een transformator kan beschrijven met behulp van het begrip fluxverandering.
|
 Opdrachten
Opdrachten
|
- (2p) Leg uit hoe je een inductiestroom opwekt. Gebruik in je antwoord het woord "flux".
- (4p) Leg in elk van de onderstaande voorbeelden uit of er een inductiestroom gaat lopen of niet.
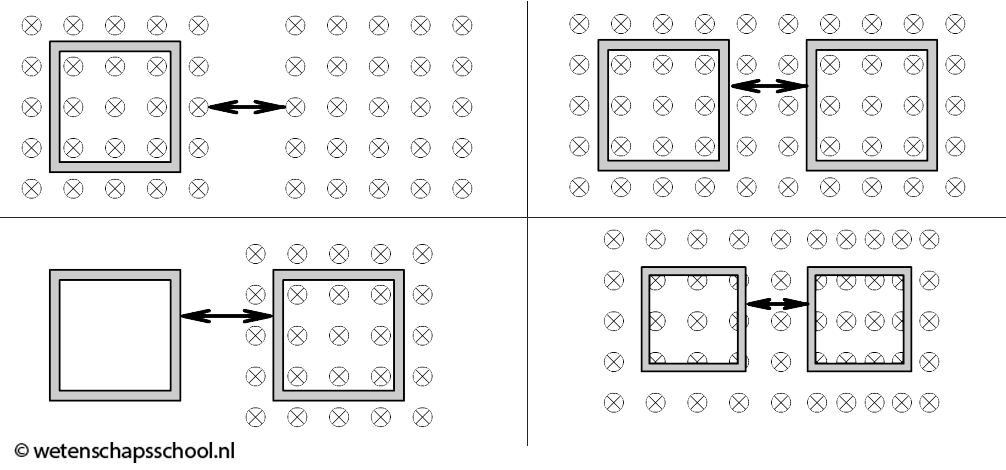
-
In de onderstaande afbeelding zien we een stroomlusje met daarin opgenomen een lampje en een metalen cilinder van 10 cm die vrij kan bewegen over twee metalen balkjes. De schakeling wordt van boven af bekeken. Over de schakeling werkt een magneetveld met een magnetische inductie van 0,10 T. Dit magneetveld wijst van boven naar beneden.
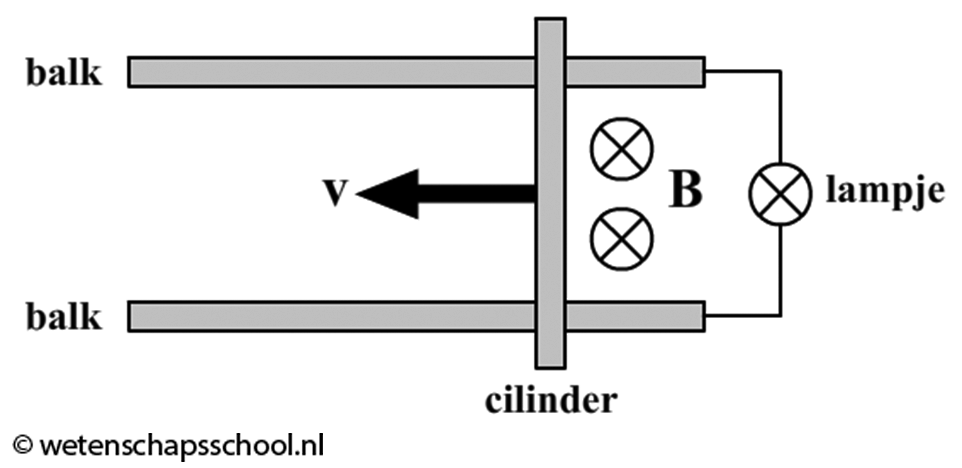
- (2p) Een persoon beweegt de cilinder handmatig naar links. Treedt er hierdoor een inductiestroom op? Leg je antwoord uit.
- (4p) Op het lampje staat dat deze optimaal brandt bij 3,0 V. Laat zien dat de cilinder met een snelheid van 300 m/s bewogen moet worden om het lampje op deze manier te laten branden. Bereken hiervoor eerst de fluxverandering die in de eerste seconde zou ontstaan.
- (4p) We zouden deze snelheid ook op een andere manier kunnen uitrekenen. Als we de cilinder weg van de lamp bewegen, dan gaat er een lorentzkracht werken op de elektronen in de cilinder. Hierdoor ontstaat aan de ene kant van de cilinder een ophoping van negatieve ladingen en aan de andere kant een ophoping van positieve ladingen. De cilinder werkt dan als een spanningsbron, waardoor er een stroom gaat lopen door het lampje. Ga na aan welke kant van de cilinder de positieve ladingen ophopen en aan welke kant de negatieve ladingen ophopen. Geef op basis van dit antwoord de stroomrichting door het lampje.
- (4p) De ophoping van ladingen aan de uiteinden van de cilinder zorgt voor een spanningsverschil. Dit spanningsverschil bouwt op totdat de elektrische kracht opgewekt door dit spanningsverschil even groot is als de lorentzkracht. Er geldt dan dus:
$$ F_{elek} = F_L $$
Bereken hiermee nogmaals de snelheid waarmee we de cilinder moeten bewegen. Gebruik hierbij dat:
$$ E = \frac{U}{d} $$
d is hier de afstand tussen de polen (oftewel de lengte van de cilinder).
-
Een spoel met 200 windingen wordt aan een krachtmeter gehangen in een homogeen magneetveld. Tussen punten P en Q wordt een spanningsbron aangesloten. In de grafiek wordt de relatie beschreven tussen de stroomsterkte in de draad en de kracht zoals deze werd afgelezen op de krachtmeter.
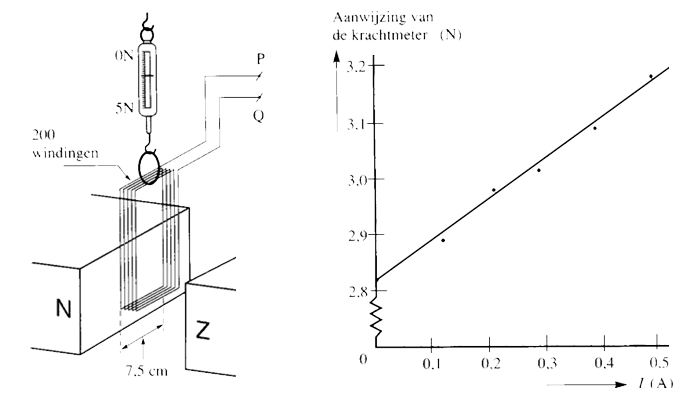
- (1p) Leg uit wat er met de spoel gebeurt als de stroomsterkte toeneemt.
- (1p) Waarom begint de grafiek niet in de oorsprong?
- (5p) Bepaal de magnetische inductie B bij een stroomsterkte van 0,4 A.
- (3p) Loopt de stroom van P naar Q of van Q naar P?
- (6p) De spanningsbron wordt afgekoppeld en de punten P en Q worden met elkaar verbonden. We trekken de spoel een stukje uit zijn evenwichtstand en laten de spoel dan los. De spoel begint hierdoor op en neer te trillen in het magneetveld. Hieronder zien we de spoel op verschillende momenten tijdens een trilling afgebeeld.
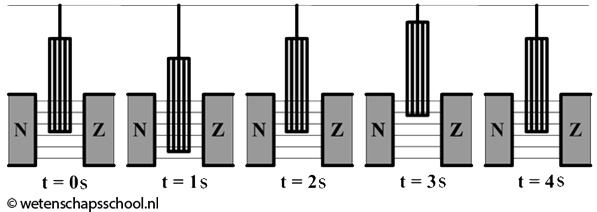
Schets een (flux,tijd)-diagram en een (spanning,tijd)-diagram, gebruikmakend van de tijden in de bovenstaande afbeelding. Geef in deze diagrammen met kruisjes aan op welke momenten de inductiestroom in de draad het grootst is.
-
(2p) Een leerling maakt een opstelling bestaande uit twee magneten en een spoel (zie de onderstaande afbeelding). De twee magneten stoten elkaar af en als gevolg blijft de tweede magneet een stuk zweven boven de eerste magneet. Door de zwevende magneet een tikje te geven, begint deze te trillen. Dankzij inductie ontstaat dan een meetbare inductiestroom in de spoel. In het rechter diagram zien we hoe deze inductiespanning verandert in de tijd. De meting is niet direct bij het loslaten van de magneet gestart.
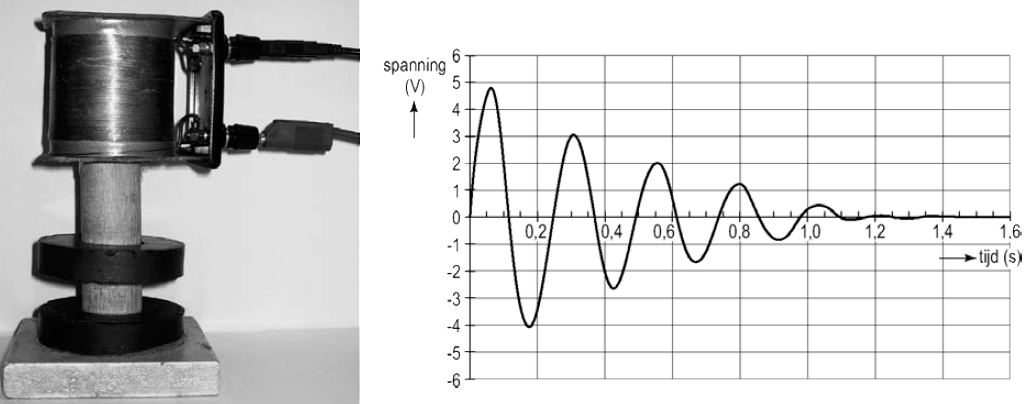
Geef in het diagram aan op welke momenten de magneet zich in zijn uiterste standen bevindt.
(bron: examen VWO 2005-2)
-
Een persoon monteert een zelfgemaakte dynamo op zijn fietswiel. De persoon doet dit door een magneet aan een spaak te bevestigen en een spoel aan de voorvork van de fiets (zie de onderstaande foto). Als het wiel ronddraait, dan beweegt de magneet periodiek langs de spoel en creëert zo een inductiespanning. In het rechter diagram is deze spanning uitgezet tegen de tijd.
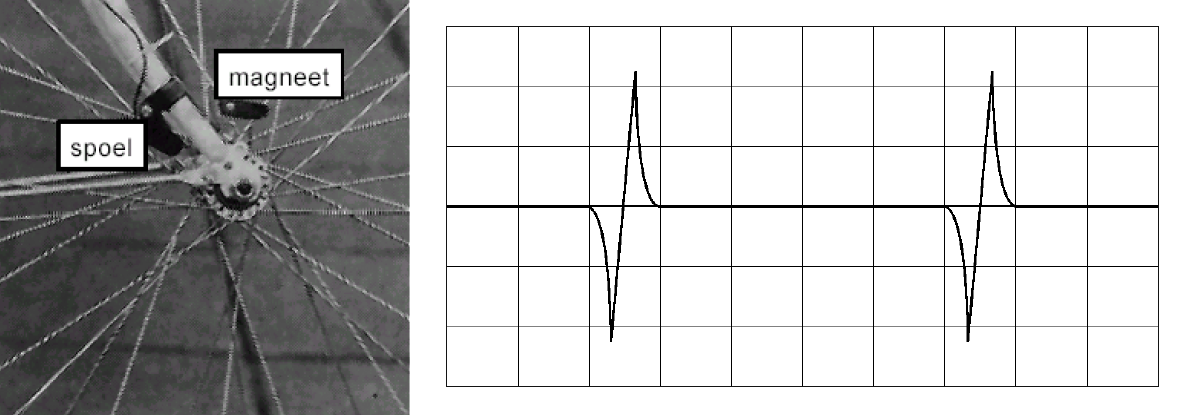
- (3p) Telkens als de magneet langskomt, wordt de spanning negatief, een moment nul en daarna positief. Leg uit waarom dit gebeurt.
- (3p) De oppervlakte onder de positieve piek is gelijk aan de oppervlakte onder de negatieve piek. Leg uit waarom dit noodzakelijk het geval moet zijn.
- (3p) Bij een inductiekookplaat wordt warmte opgewekt in de metalen bodem van een pan door middel van inductie. In de inductiekookplaat zit namelijk een spoel die aangesloten is op een wisselspanning. Leg uit hoe de pan verwarmd wordt door de inductiekookplaat.
- (4p) Een transformator kan worden gebruikt om spanning te verhogen of verlagen. Een dergelijk apparaat zit bijvoorbeeld in de adapter van een laptop. Hiermee wordt de 230 V van het stopcontact verlaagt naar een spanning waarop de laptop goed functioneert. Een transformator bestaat uit twee spoelen (zie de onderstaande afbeelding).
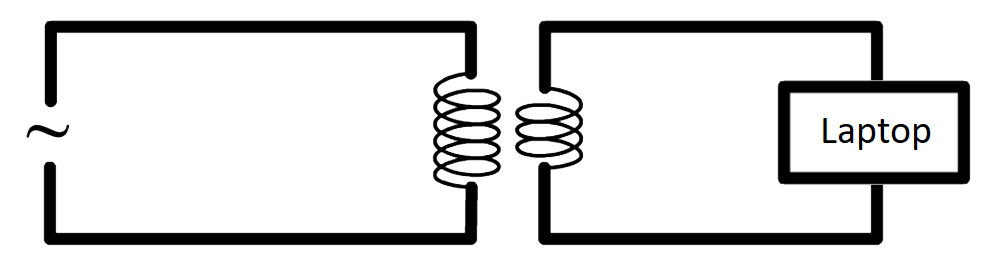
Leg uit hoe de transformator werkt. Leg ook uit waarom een transformator alleen werkt met een wisselspanning.
- (6p) Een leerling sleept een vierkant stroomlusje met zijden van 10 cm een homogeen magneetveld binnen. De sterkte van het magneetveld is 0,10 T. De leerling trekt het lusje met een snelheid van 30 cm/s het magneetveld in. In het stroomlusje is ook een weerstand van 5,0 mΩ en een ampèremeter toegevoegd. Bereken wat de ampèremeter aan zal geven.
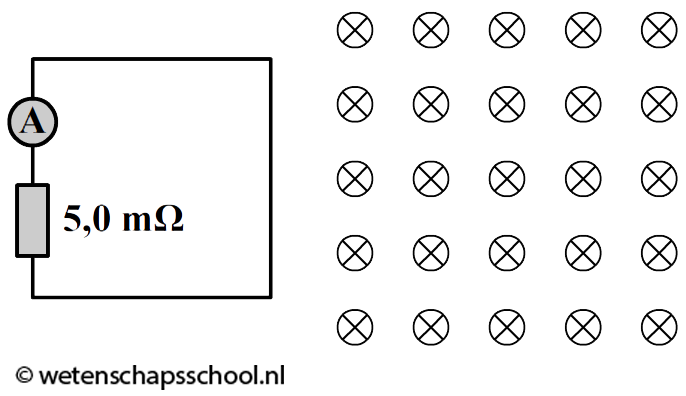
- (4p) Als we een magneet door een metalen buisje gooien, dan zal de magneet een stuk langzamer vallen dan je misschien zou verwachten. Leg uit hoe dit komt.
- (3p) Je laat een magneet door een stroomlusje vallen. In de onderstaande afbeelding zie je de magneet op verschillende momenten van de val. Schets in de onderstaande twee diagrammen hoe de flux en de spanning in de tijd zullen veranderen in de lus.
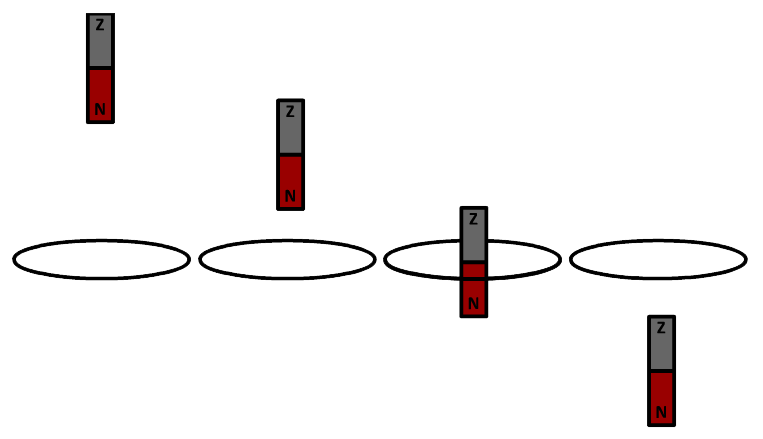

-
Een persoon roteert een vierkante stroomlus in een homogeen magneetveld (zie de onderstaande afbeelding). De magnetische inductie van het veld is 0,50 T en de stroomlus heeft zijden van elk 3,0 cm.

- (6p) Bereken (!) in de drie bovenstaande afbeeldingen de flux. In de tweede afbeelding staat de stroomlus onder een hoek van 45 graden met de horizon.
- (3p) De lus draait met een omlooptijd van 1,0 seconde. Maak een (φ,t)-diagram van een volledige omlooptijd.
- (2p) Geef aan in welk van de bovenstaande afbeeldingen de inductiespanning nul is en in welke maximaal. Licht je antwoord toe.
- (2p) Bij het roteren wordt automatisch een wisselspanning opgewekt. Leg uit dat dit het geval is.
- (5p) Maak nu een (U,t)-diagram van een volledige omlooptijd. Bedenk hiervoor eerst hoe je de maximale inductiespanning kan bepalen met behulp van de grafiek die je bij vraag b getekend hebt.
|
| BINAS: |
|
| 7 |
Constante van Coulomb en elektronlading |




 Demonstratievideo
Demonstratievideo

 Voorbeeld
Voorbeeld
 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten


 Demonstratievideo
Demonstratievideo


 (Afbeelding: Marjory Collins; Library of Congress; PD)
(Afbeelding: Marjory Collins; Library of Congress; PD)
 (Afbeelding: Boyce Duprey; CC BY 2.0)
(Afbeelding: Boyce Duprey; CC BY 2.0)



 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten

 Demonstratievideo
Demonstratievideo

 Demonstratievideo
Demonstratievideo
 Demonstratievideo
Demonstratievideo


 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten

 Demonstratievideo
Demonstratievideo



 Demonstratievideo
Demonstratievideo


 Leerdoelen:
Leerdoelen:
 Opdrachten
Opdrachten