Hoofdstuk 1
Geluid
§1 Trillingen en golven §2 Trillingstijd en frequentie §3 De oscilloscoop §4 De geluidsnelheid §5 Geluidsterkte
§1 Geluid
In dit hoofdstuk gaan we geluid bestuderen. Het is hiervoor eerst nodig iets te leren over trillingen en golven.
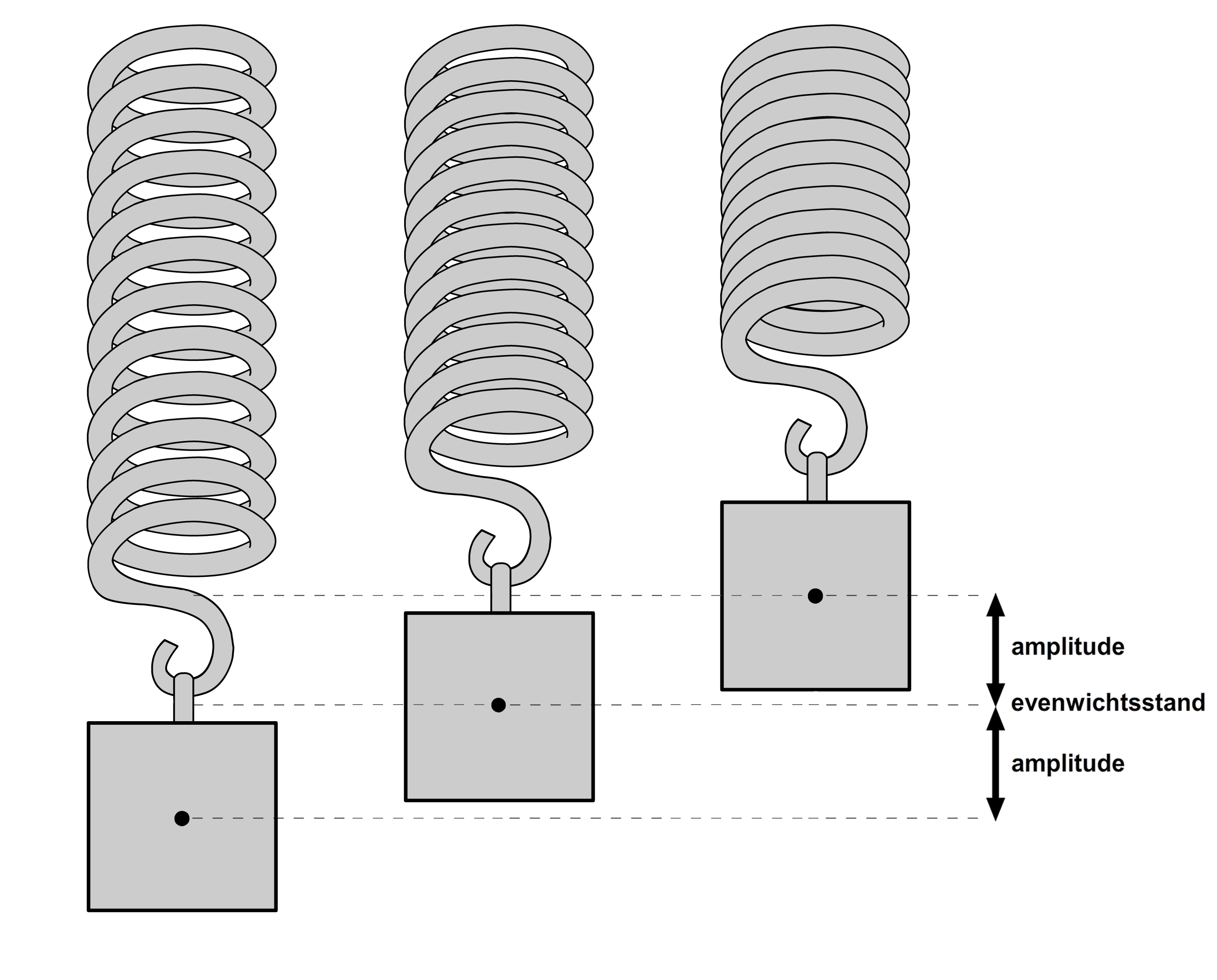
Een trilling is het simpel heen en weer bewegen van een voorwerp. Hieronder zien we twee voorbeelden. Links zien we een slinger (een balletje aan een touwtje) die heen en weer beweegt. En rechts zien we een blokje dat op en neer beweegt aan een veer (zie ook de onderstaande animatie).
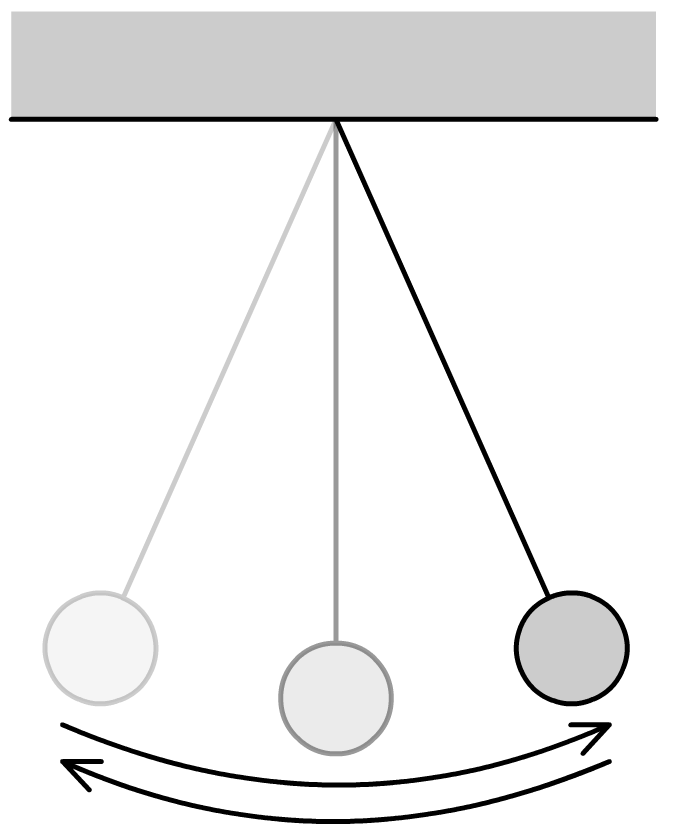
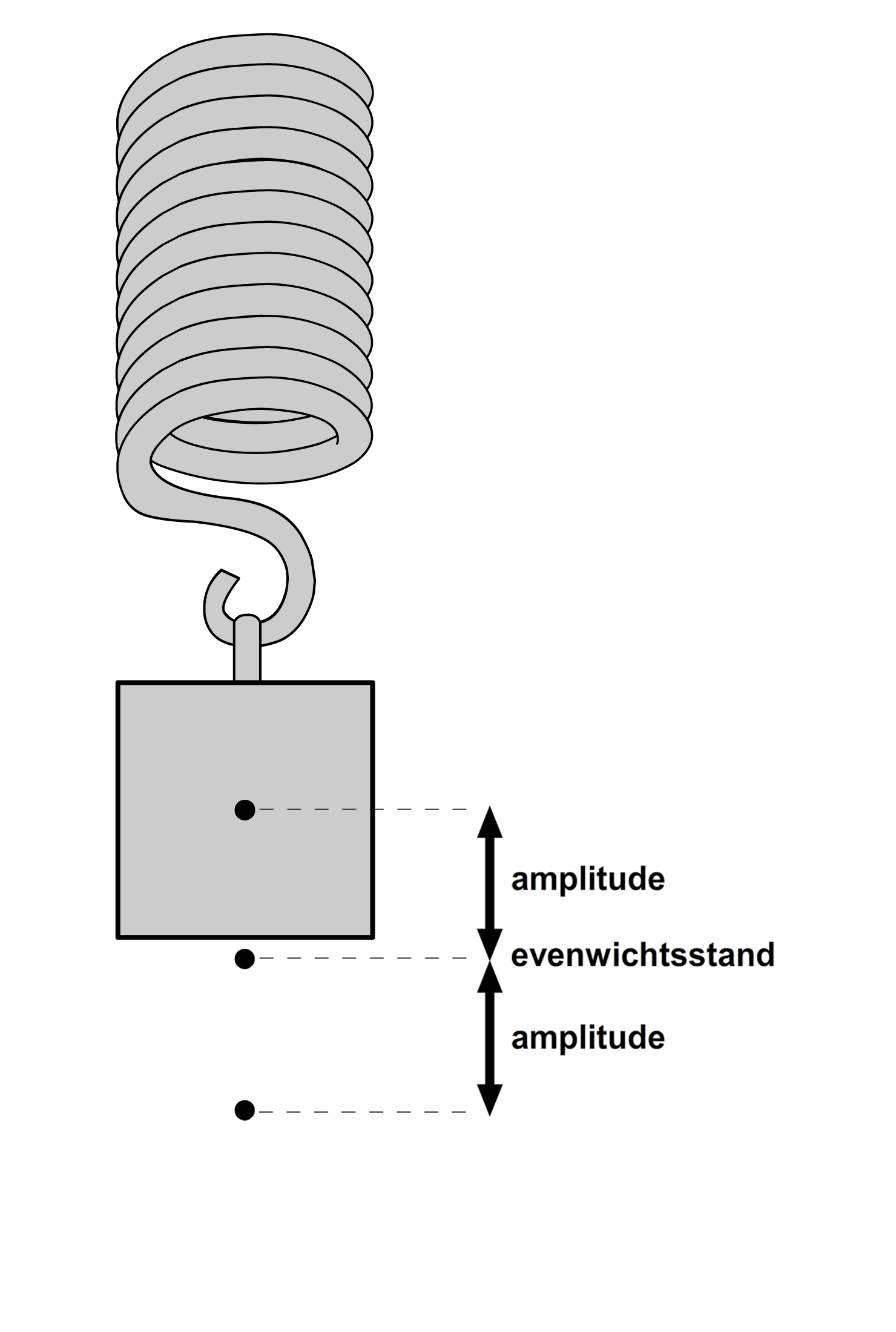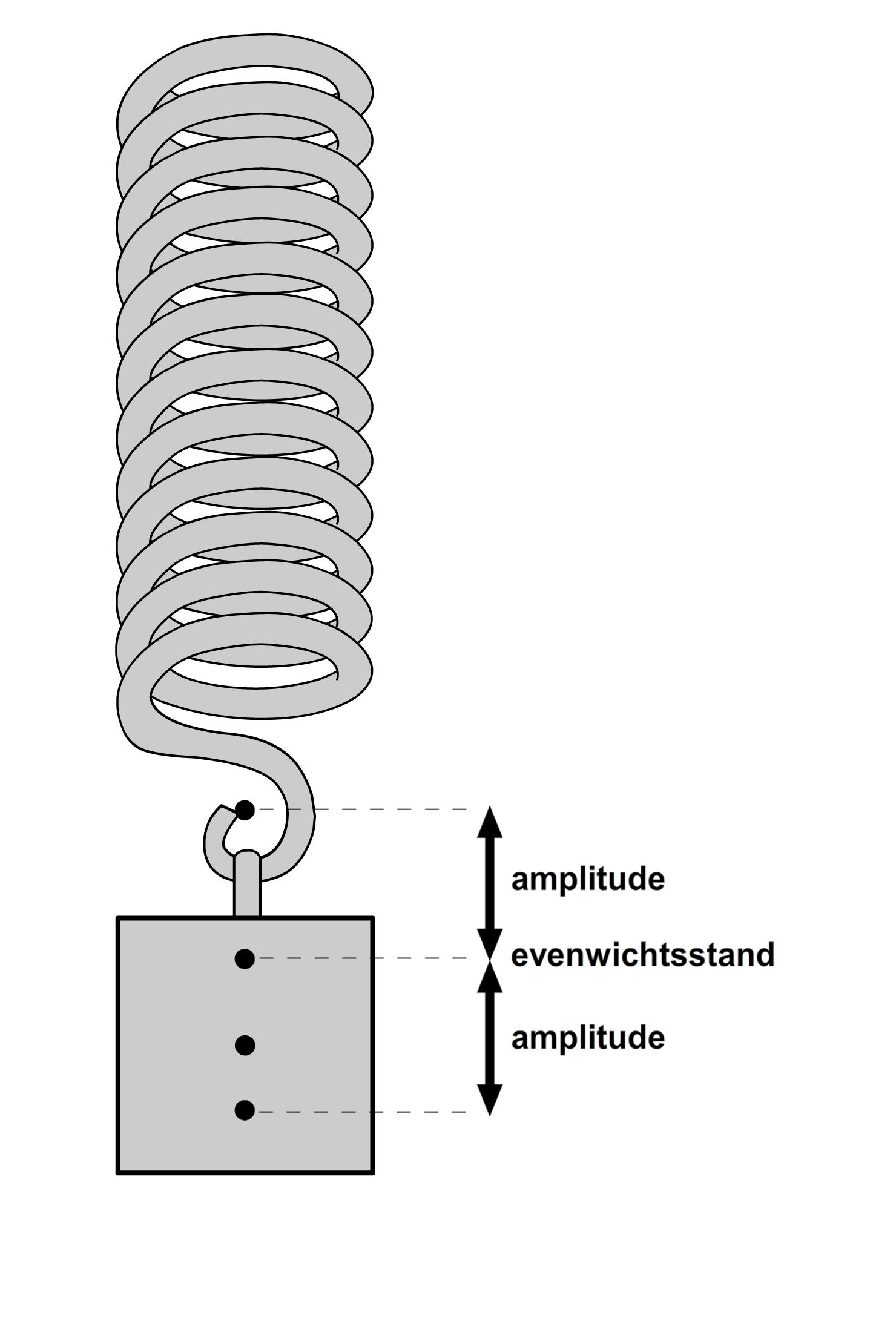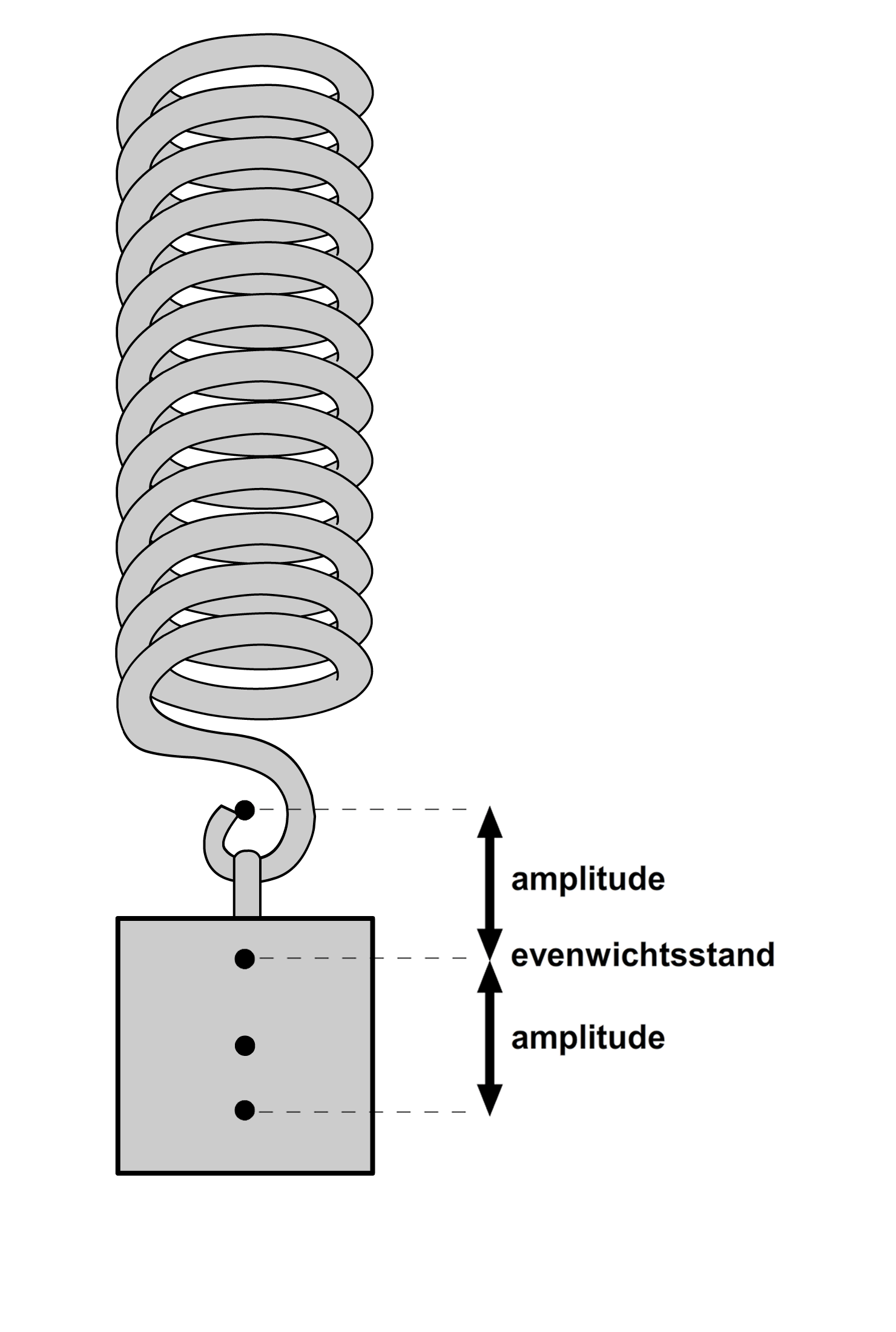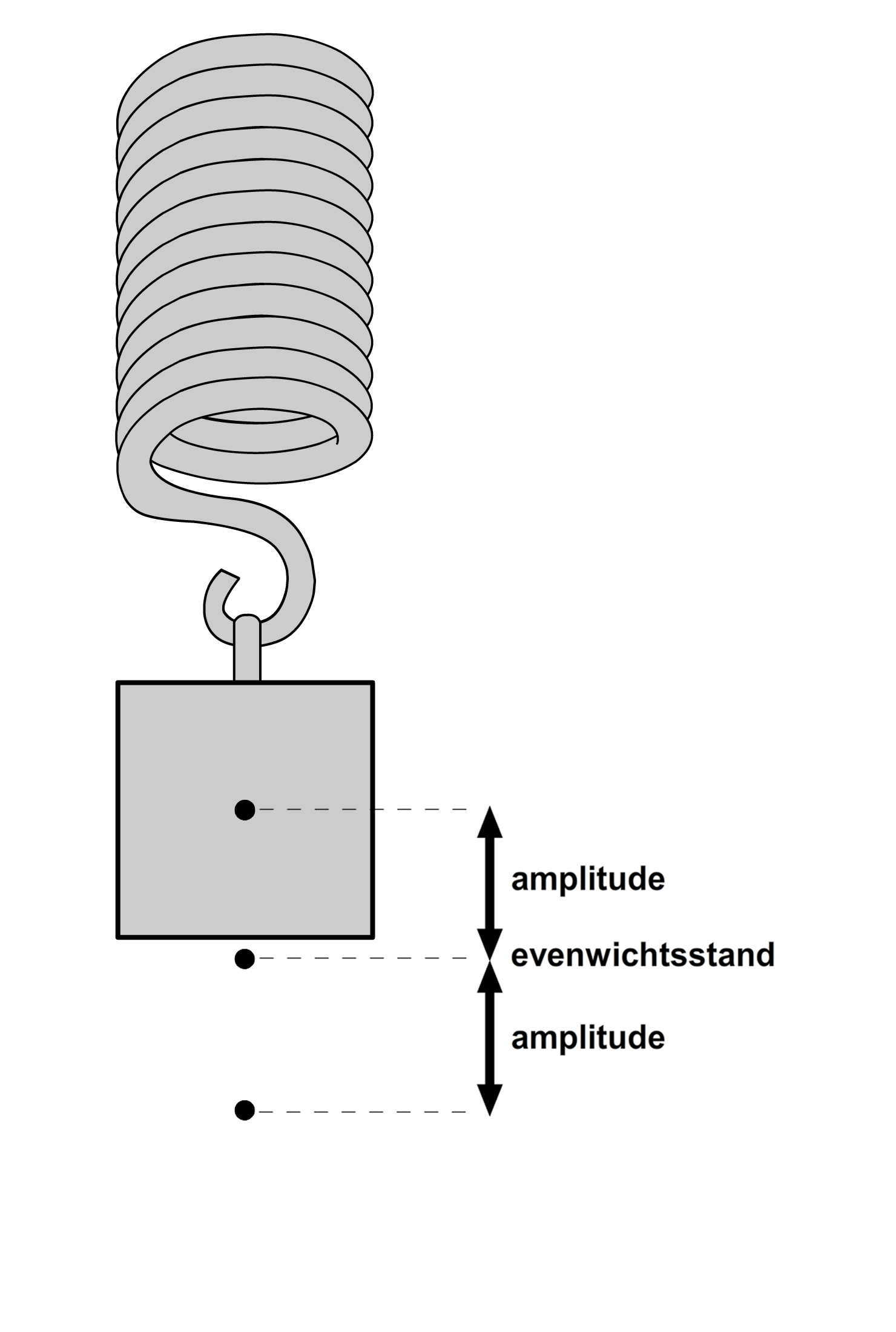
Zoals je ziet, beweegt het blokje aan de veer om een bepaald middelpunt. We noemen dit de evenwichtsstand (zie de onderstaande afbeelding). De afstand dat het blokje verwijderd is van deze evenwichtsstand noemen we de uitwijking. De maximale uitwijking van het blokje tijdens de trilling noemen we de amplitude.
Hieronder is een animatie van een golf in een touw te zien. Hieronder zien we een afbeelding van een golf. Op de website, kan je een animatie zien van het ontstaan van deze golf. Door het touw aan de linkerkant op en neer te bewegen, komt het hele touw in beweging. Elk stukje van het touw brengt het volgende stukje in beweging. We noemen de resulterende beweging een golf. Omdat de golf zich naar rechts verplaatst door het touw spreken we van een lopende golf.
Net als in een touw, kunnen ook in de lucht golven ontstaan. Dit worden geluidsgolven genoemd. Bij het waarnemen van geluid hebben we drie elementen nodig:
- Een geluidsbron
- Een tussenstof
- Een ontvanger
Laten we beginnen met de geluidsbron. Een geluidsbron bevat een trillend onderdeel dat de lucht in trilling brengt. In de onderstaande afbeelding is de geluidsbron een luidspreker (ook wel een speaker genoemd). Andere voorbeelden van geluidsbronnen zijn mmuziekinstrumenten en onze stembanden.
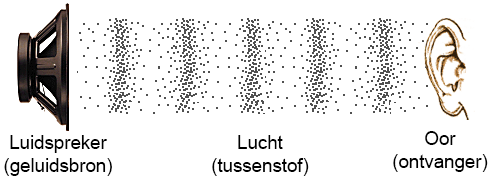
Het bewegende onderdeel in een luidspreker heet de conus. Als de conus heen en weer beweegt, dan botst het tegen de omliggende luchtdeeltjes en deze luchtdeeltjes botsen weer tegen de volgende deeltjes etc. Als gevolg ontstaat er een geluidsgolf door de lucht (zie de onderstaande animatie). De lucht noemen we in dit geval de tussenstof. Dit is de stof waardoor het geluid zich kan verplaatsten.
Lucht is trouwens niet de enige tussenstof. In elk materiaal kunnen geluidsgolven ontstaan. In metalen bijvoorbeeld, kunnen geluidsgolven zelfs nog sneller voortplanten dan in de lucht. In de ruimte is geen tussenstof aanwezig. We spreken dan van een vacuüm. In een vacuümruimte kan geluid niet voortplanten.
 Demonstratievideo
Demonstratievideo
| ||
|
We nemen geluid pas waar als geluidsgolven aankomen bij een ontvanger. Een voorbeeld is het trommelvlies in ons oor. Dit kan in trilling worden gebracht door deze geluidsgolven en zo nemen we geluid waar. Een ander voorbeeld van een ontvanger is een microfoon.
We eindigen deze paragraaf met een beschrijving van de luidspreker en de microfoon. In de onderstaande afbeelding zien we een doorsnede van een simpele luidspreker. De luidspreker bestaat uit drie onderdelen: de conus, een spoel en een magneet. Aan de conus is een spoel verbonden. Door verschillende patronen van stroompjes door de spoel te sturen, ontstaat om de spoel een wisselend magneetveld. Een permanente magneet in de speaker reageert op dit magneetveld door de conus aan te trekken en af te stoten. Als gevolg gaat de conus trillen.
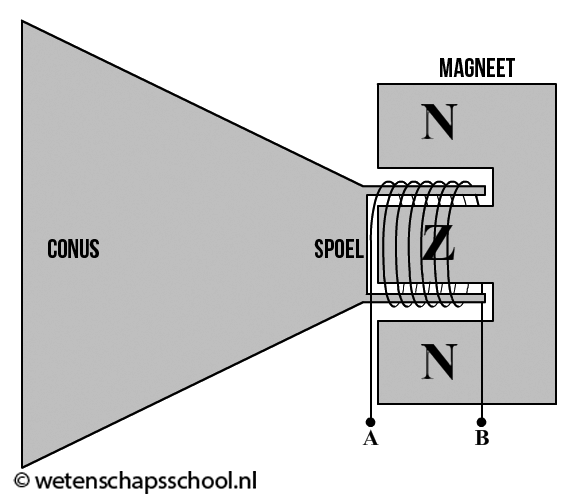
De werking van een microfoon lijkt op de werking van de speaker. In dat geval zorgen geluidsgolven in de lucht er juist voor dat de conus en dus ook de spoel gaan trillen. Als een spoel trilt in de buurt van een magneet, dan ontstaat een patroon van stroompjes. Dit patroon kan worden opgeslagen door een computer of het kan versterkt via een luidspreker weer hoorbaar gemaakt worden.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§2 Trillingstijd en frequentie
In deze paragraaf gaan we nauwkeuriger de trilling bestuderen. Dit doen we met de begrippen trillingstijd en frequentie.
In deze paragraaf gaan we het hebben over de trillingstijd (T), ook wel de periode genoemd. Zoals de naam al verklapt vertelt dit ons hoelang één trilling duurt.
Met de trillingstijd kunnen we ook de frequentie (f) berekenen. De frequentie vertelt ons hoeveel trillingen een voorwerp in een seconde maakt. We meten de frequentie meestal in hertz (Hz). Dit komt dus overeen met het aantal trillingen per seconde. Een frequentie van 100 Hz wil dus zeggen dat een voorwerp 100 keer per seconde heen en weer beweegt.
We kunnen als volgt met de frequentie en de trillingstijd rekenen:
$$ f = \frac{1}{T} \,\,\,\,\,\text{(SI-eenheden)} $$
|
Let erop dat je de trillingstijd in deze formule altijd in seconde invult. Als de trillingstijd in een vraag in bijvoorbeeld milliseconden (ms) wordt gegeven, dan moet je dit eerst nog even omschrijven naar seconde. Er geldt:
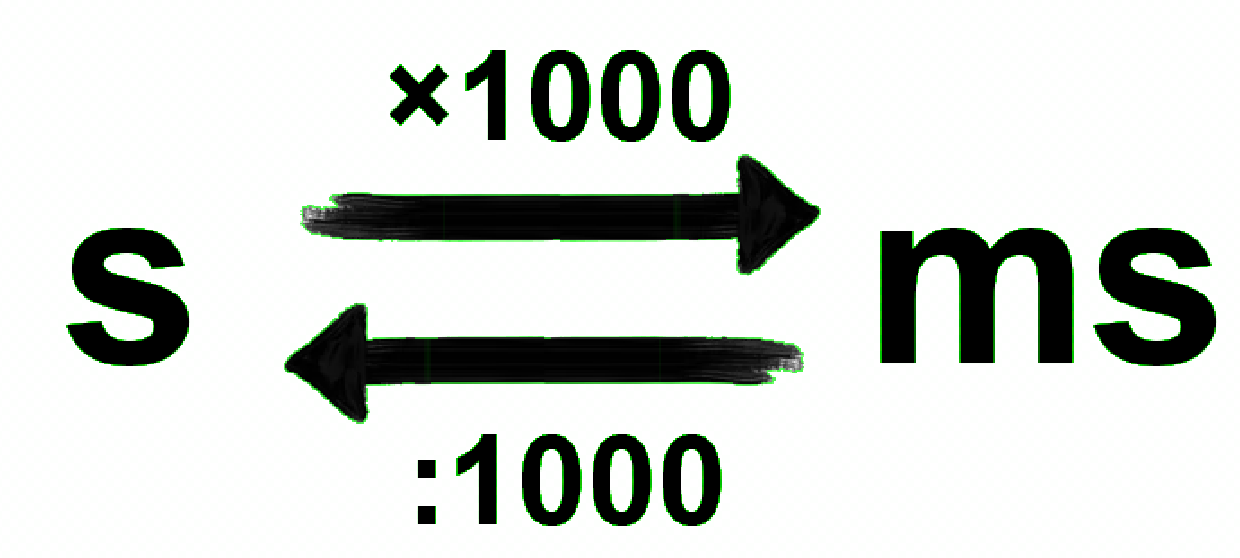
Aan de formule "f = 1/T" kan je ook zien dat een grotere frequentie altijd zorgt voor een kleinere trillingstijd en andersom. In de volgende paragraaf gaan we dit toepassen.
In de volgende voorbeelden gaan we leren rekenen met deze formule:
 Voorbeeld
Voorbeeld
|
|
Vraag: Een vlag wappert met een frequentie van 0,25 Hz heen en weer. Wat is de trillingstijd van deze beweging? Antwoord: Stap 1: Gegevens (G) f = 0,25 Hz Stap 2: Omschrijven (O) De trillingstijd moet in deze formule in seconden worden gegeven. De trillingstijd is in deze vraag echter helemaal niet gegeven. We kunnen deze stap dus overslaan. Stap 3: Formule (F) Noteer de formule in de juiste vorm. We willen de trillingstijd weten, dus we gebruiken: $$ T = \frac{1}{f} $$Stap 4: Invullen en Rekenen (IR) Vul de formule in: $$ T = \frac{1}{0,25} = 4,0 \text{ s} $$Stap 5: Eenheid (E) Check of de eenheid achter het antwoord staat. In dit geval is dit s.
|
 Voorbeeld
Voorbeeld
|
|
Vraag: Bij het aanslaan van een stemvork ontstaat een toon met een trillingstijd van 2,2727 ms. Bereken de frequentie van deze stemvork.Antwoord: Stap 1: Gegevens (G) Trillingstijd = 2,2727 ms Stap 2: Omschrijven (O) De trillingstijd moet in deze formule in seconden worden gegeven. Trillingstijd = 2,2727 / 1000 = 0,0022727 s Stap 3: Formule (F) Noteer de formule in de juiste vorm. We willen de frequentie weten, dus we gebruiken: $$ \text{frequentie} = \frac{1}{\text{trillingstijd}} $$Stap 4: Invullen en Rekenen (IR) Vul de formule in: $$ \text{frequentie} = \frac{1}{0,0022727} = 440 \text{ Hz} $$Stap 5: Eenheid (E) Check of de eenheid achter het antwoord staat. In dit geval is dit Hz.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§3 De oscilloscoop
In deze paragraaf gaan we de kennis uit de vorige paragraaf toepassen om het verschil tussen harde, zachte, lage en hoge tonen te begrijpen. We doen dit met behulp van een zogenaamde oscilloscoop.
In een eerdere paragraaf hebben we gelezen dat geluid wordt veroorzaakt door het trillen van luchtdeeltjes. We kunnen deze trillingen zichtbaar maken met een oscilloscoop. In de onderstaande afbeelding zien we rechts een oscilloscoop. Hierop is een microfoon aangesloten. Zoals we in de vorige paragraaf geleerd hebben zet een microfoon geluid om in elektrische stroompjes. Deze stroompjes worden zichtbaar gemaakt op het scherm van de oscilloscoop. Links zien we een zogenaamde stemvork. Dit is een simpel metalen instrument dat met een hamertje aangeslagen kan worden. De stemvork produceert dan de "nette" toon die op het scherm zichtbaar is.

 EXPERIMENT
EXPERIMENT
| ||
|
Het oscilloscoopbeeld kan worden opgevat als een diagram met op de horizontale as de tijd (t) en op de verticale as de uitwijking (u) (zie de onderstaande afbeelding).
De onderstaande trilling herhaalt zich in de tijd. We noemen een dergelijke beweging een periodieke beweging. Zoals we eerder hebben geleerd geeft de trillingstijd of periode aan hoelang het duurt voordat een beweging zich herhaalt. In de onderstaande afbeelding zien we twee manieren om de trillingstijd te meten. Ook is de evenwichtsstand en de amplitude aangegeven.
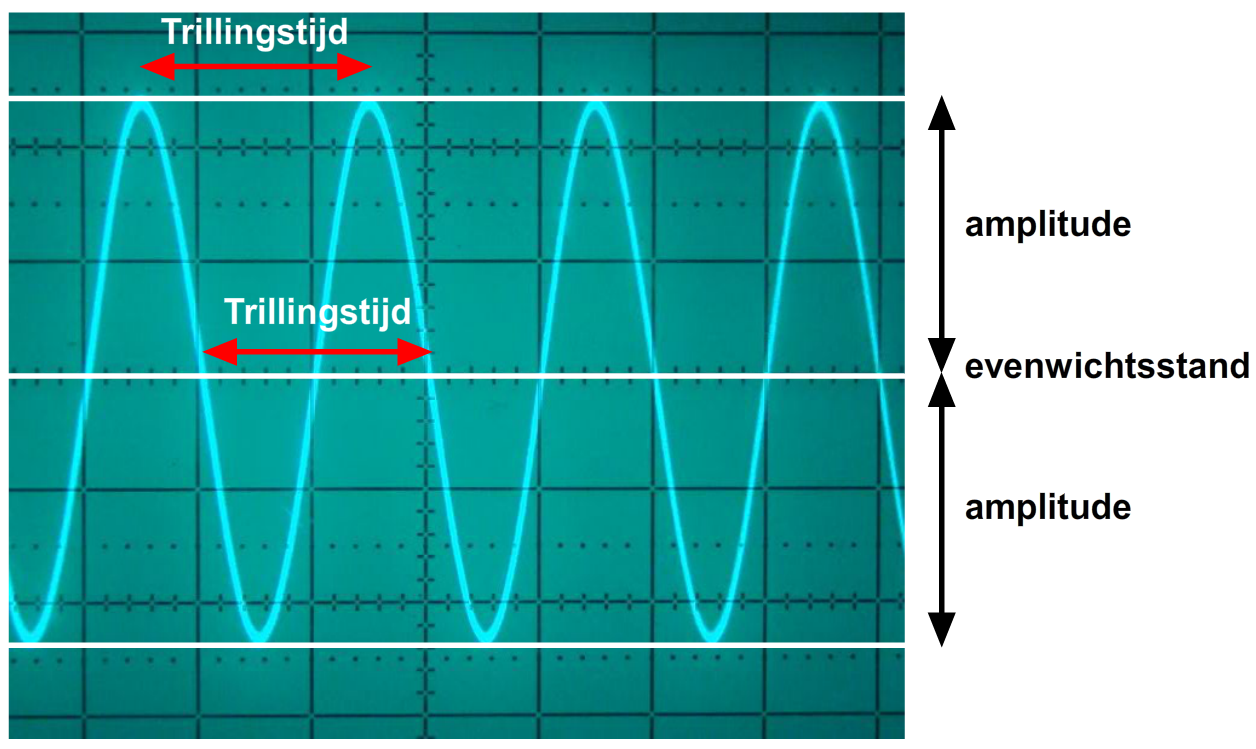
De stapgrootte op de horizontale as van het oscilloscoopbeeld wordt gegeven in ms/div. "div" staat hier voor "division", hetgeen we in het Nederlands "hokje" zouden noemen. Een waarde van 10 ms/div betekent bijvoorbeeld dat elk hokje op de horizontale as overeenkomt met 10 milliseconden.
 Voorbeeld
Voorbeeld
|
|
Vraag: Bepaal de frequentie van het onderstaande oscilloscoopbeeld van een stemvork. De oscilloscoop is ingesteld op 2 ms/div.
Antwoord: Eén trillingstijd komt hier overeen met 3,0 hokjes. Omdat de oscilloscoop is ingesteld op Dit rekenen we om naar seconde: $$ T = \frac{6,0}{1000} = 0,006 \text{ s} $$Met de formule voor de frequentie vinden we dan: $$ f = \frac{1}{T} $$ $$ f = \frac{1}{0,006}= 167 \text{ Hz} $$
|
 Voorbeeld
Voorbeeld
|
|
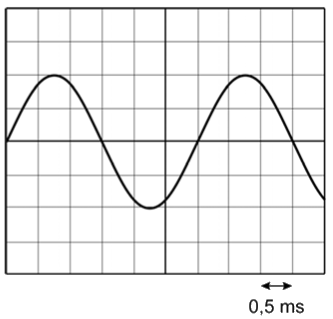
Vraag: Bepaal de frequentie van het onderstaande oscilloscoopbeeld van een saxofoon. De oscilloscoop is ingesteld op 5 ms/div.
Antwoord: De tijdsduur behorende bij één trilling is in dit geval lastig nauwkeurig af te lezen. Het is hier daarom noodzakelijk om de trillingstijd van zoveel mogelijk trillingen tezamen te meten. Als we netjes meten, dan vinden we bijvoorbeeld dat 10 trillingen overeenkomen met 4,75 hokjes (ga dit zelf na). Eén trilling komt dan overeen met: $$ \frac{4,75}{10} = 0,475 \text{ hokjes} $$Omdat de oscilloscoop is ingesteld op 5 milliseconde per hokje, vinden we: $$ 0,475 \times 5 = 2,375 \text{ ms} $$Dit rekenen we om naar seconde: $$ T = \frac{2,375}{1000} = 0,002375 \text{ s} $$Met de formule voor de frequentie vinden we dan: $$ f = \frac{1}{T} \;\;\;\;\;\;\;\; f = \frac{1}{0,002375} = 421 \text{ Hz} $$
|
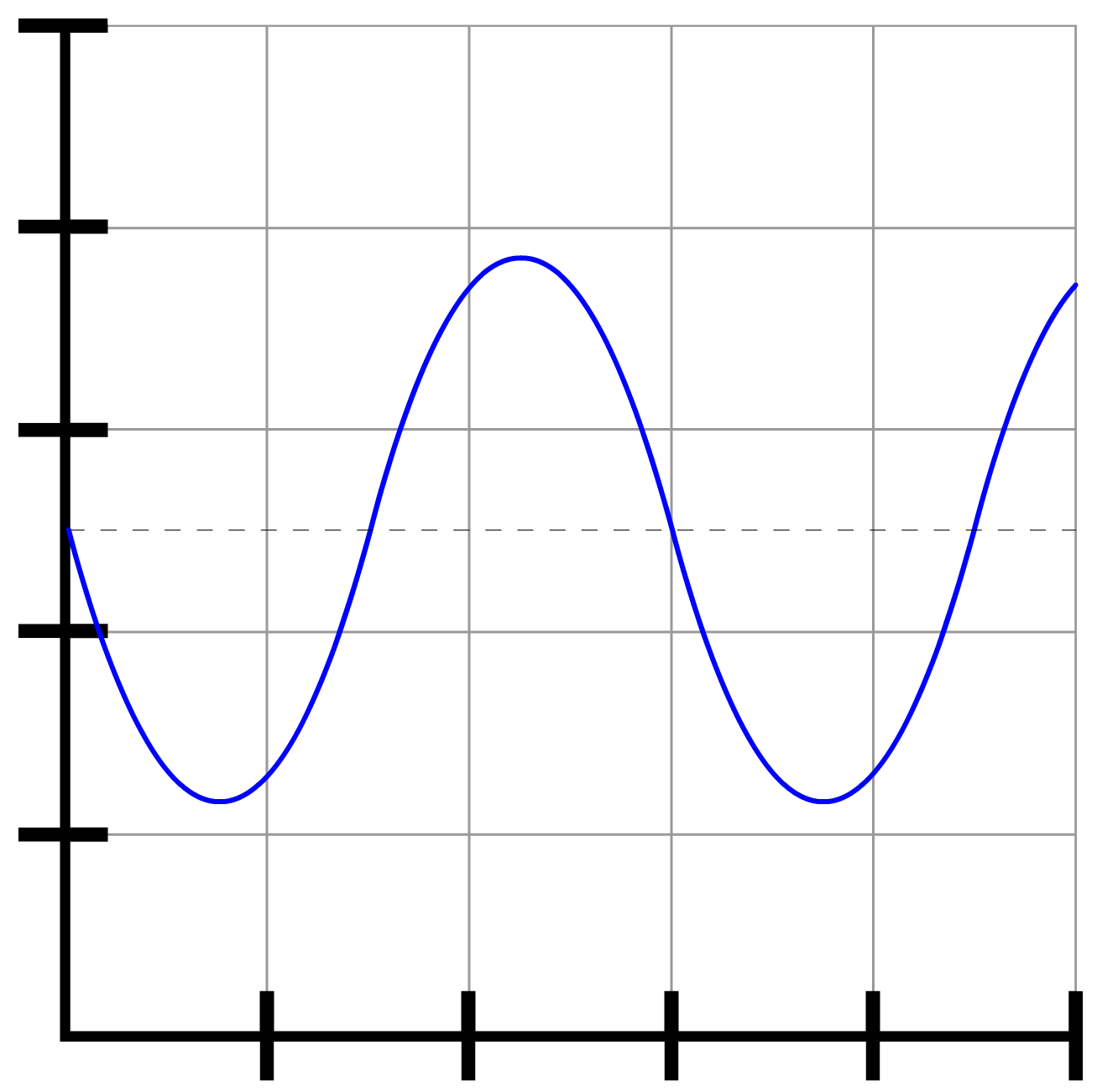
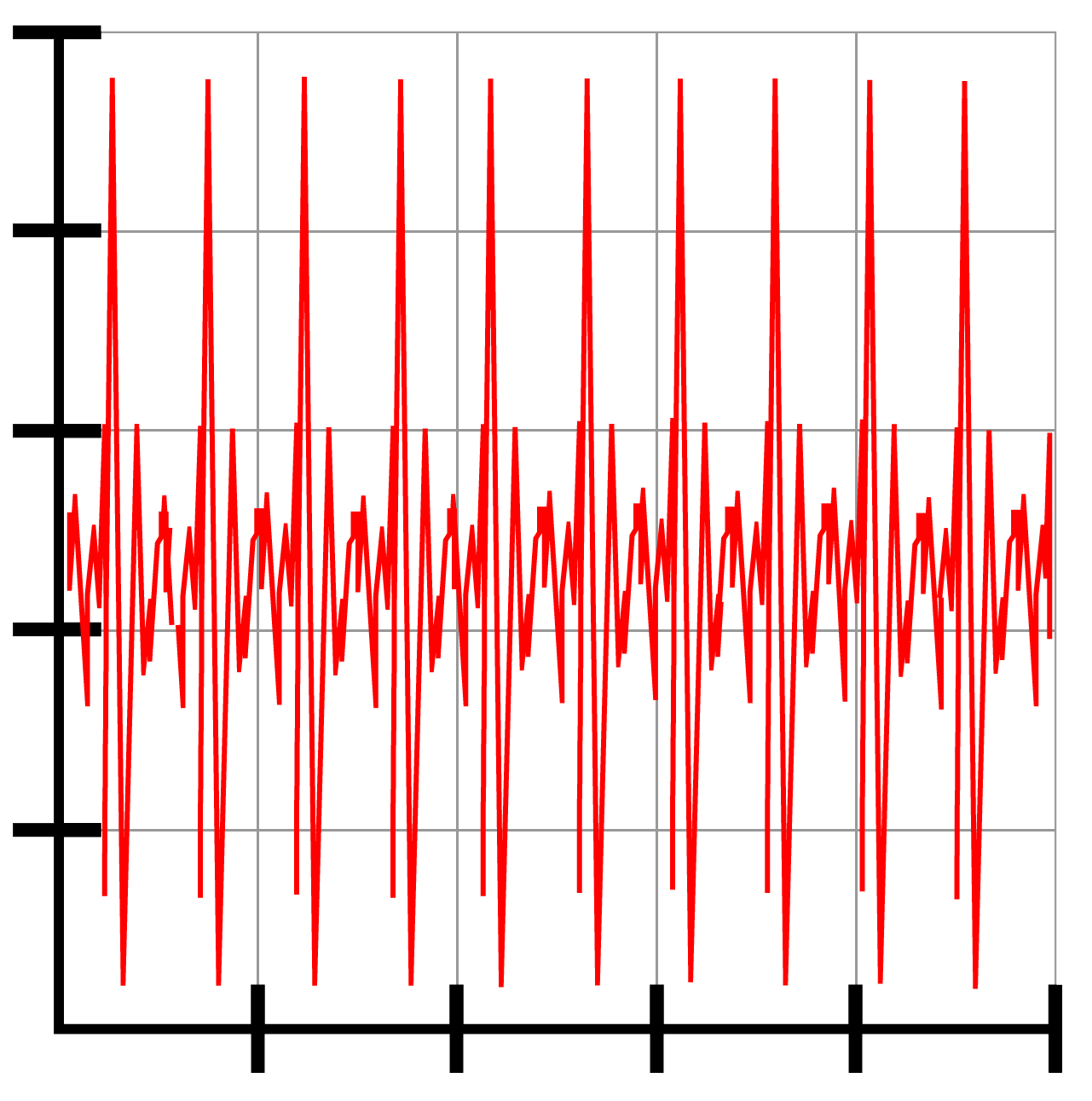
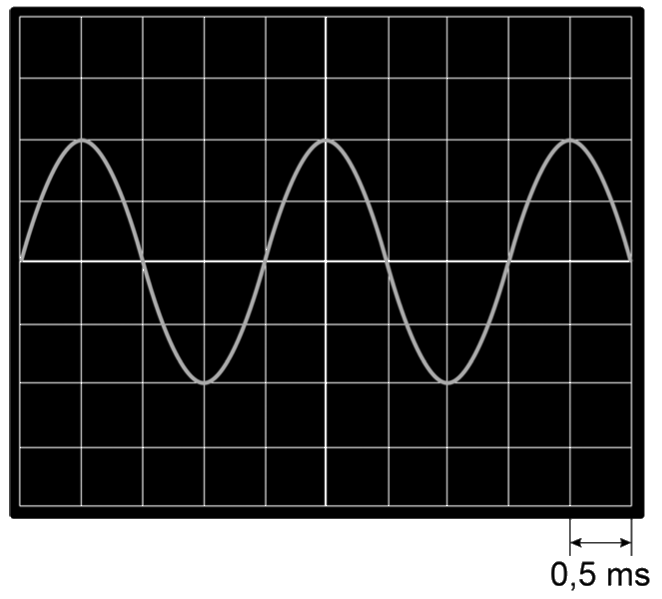
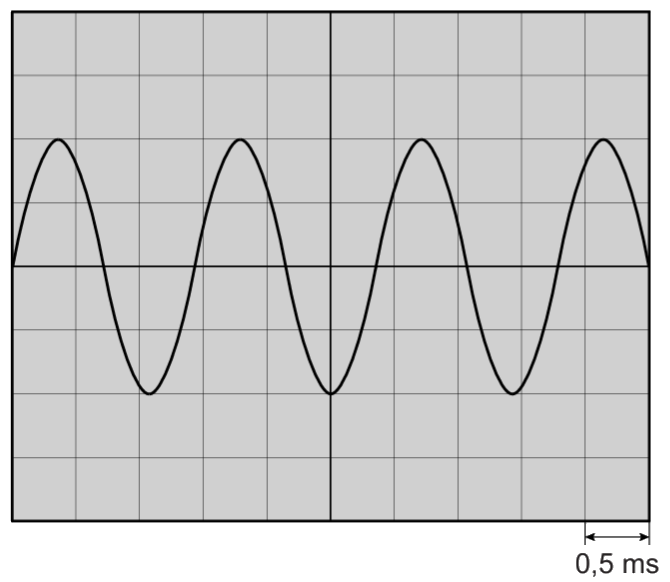
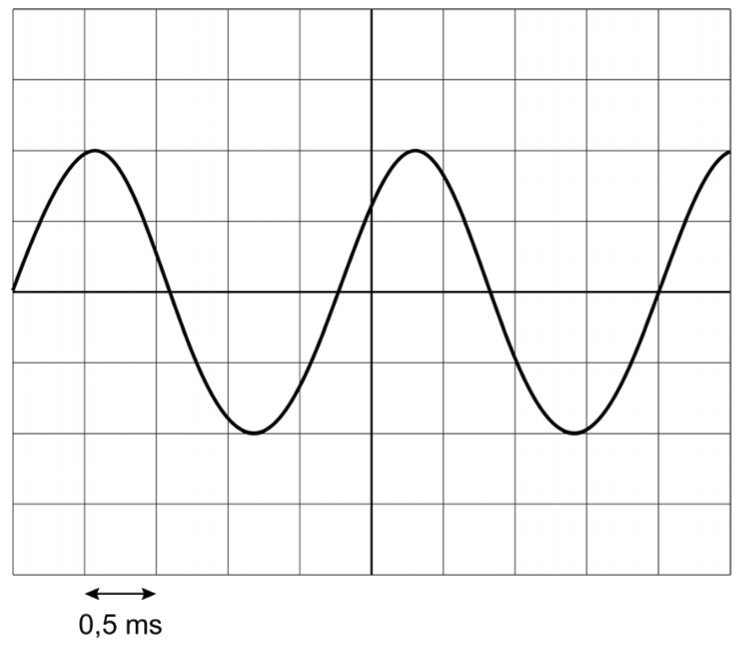
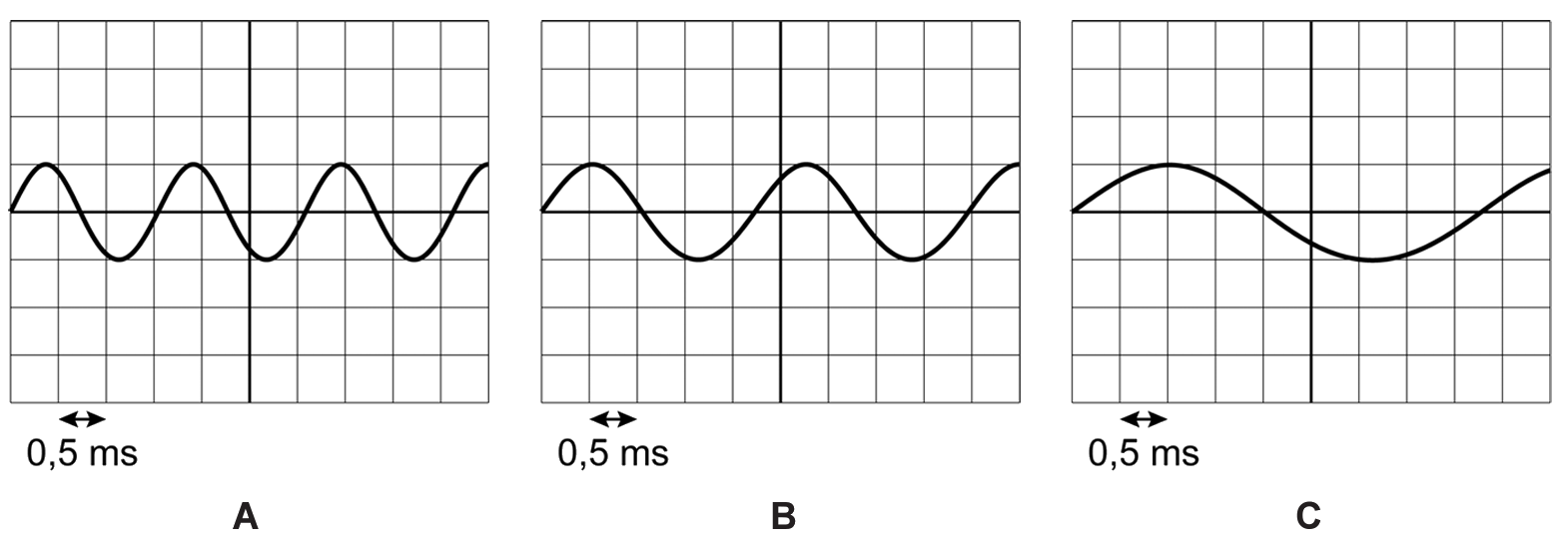
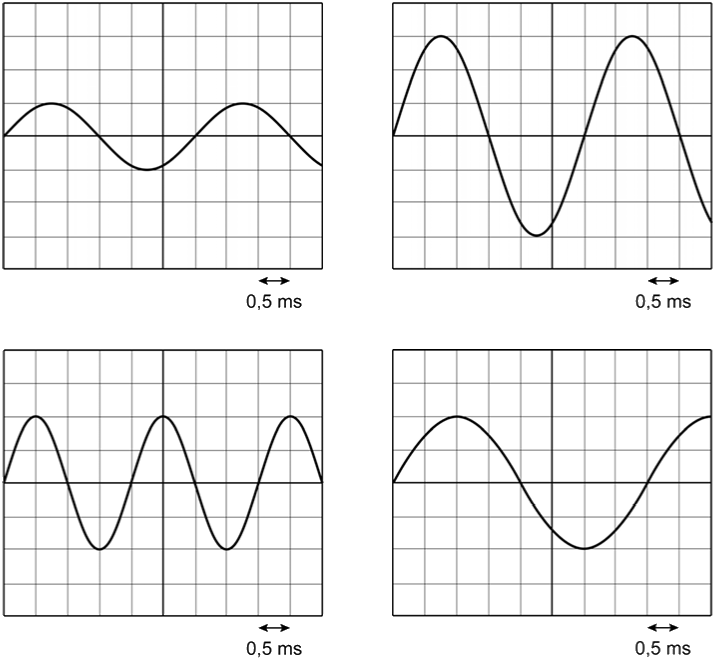
Laten we eens het oscilloscoopbeeld van een aantal tonen vergelijken. Hieronder zien we aan de linkerzijde een oscilloscoopbeeld van een zachte en een harde toon. De "hardheid" van het geluid noemen we in de natuurkunde de geluidsterkte. Zoals je kunt zien heeft een zachte toon een kleine amplitude en heeft de harde toon een grote amplitude.
Aan de rechterkant zien we een oscilloscoopbeeld van een lage en een hoge toon. Zoals je kunt zien heeft een lage toon een lage frequentie (en een grote trillingstijd) en heeft een hoge toon een hoge frequentie (en een lage trillingstijd). De frequentie van een toon bepaald dus de toonhoogte van het geluid.
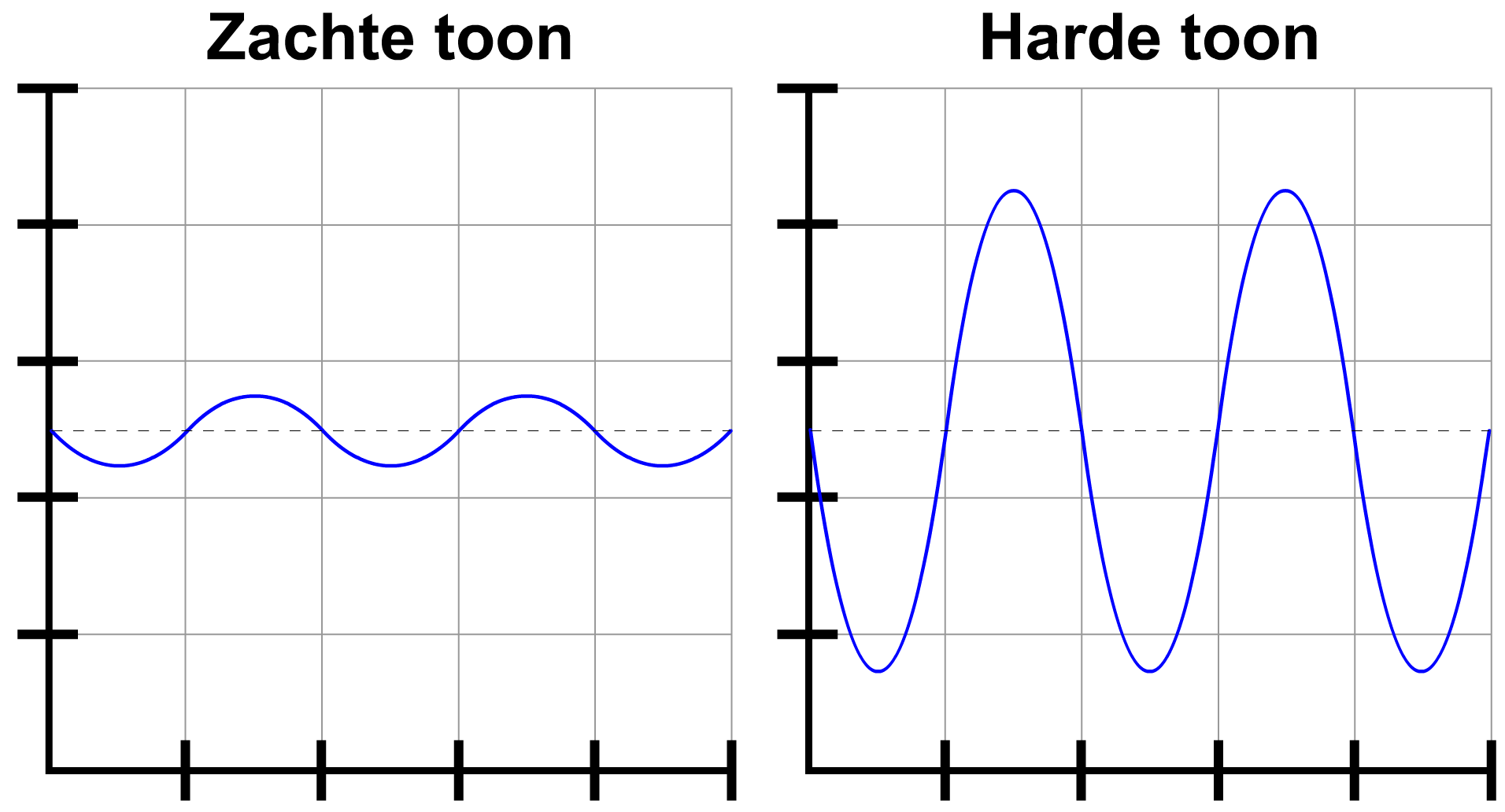
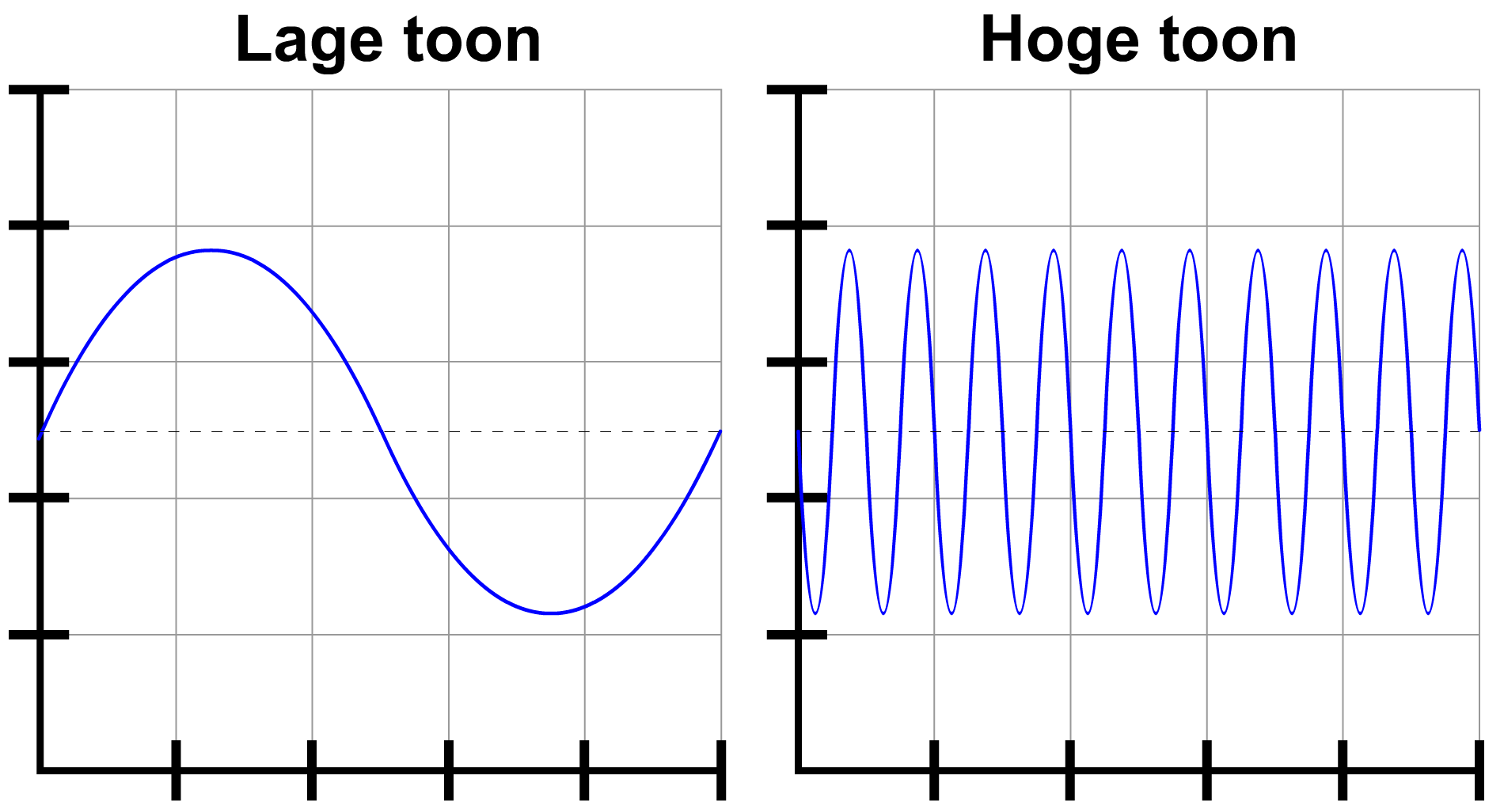
 EXPERIMENT
EXPERIMENT
| ||
|
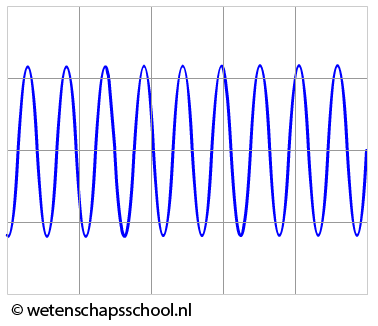
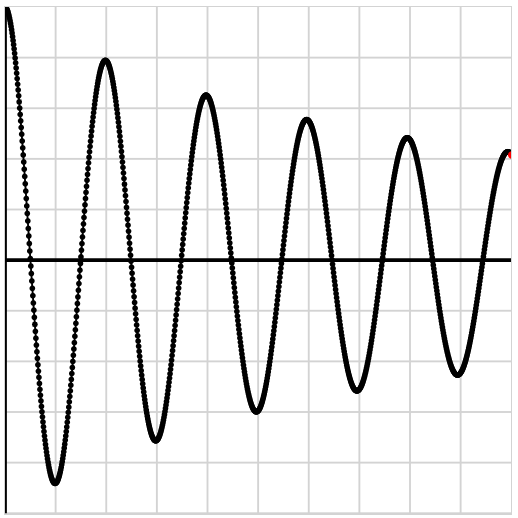
Als we een stemvork aanslaan, dan is het geluid eerst hard te horen en na verloop van tijd wordt het steeds zachter. We zien dit effect in het onderstaande oscilloscoopbeeld. Zoals je kan zien wordt hier de amplitude steeds kleiner. De trillingstijd en de frequentie, en dus ook de toonhoogte, blijven gelijk.
Een simpel muziekinstrument waarmee we tonen kunnen produceren met verschillende frequenties is een snaar. Dit is een dunne draad die onder spanning staat. De frequentie en dus ook de toonhoogte van een snaar kan als volgt verhoogd worden:
- Door de snaar strakker aan te spannen.
- Door de snaar korter te maken.
- Door een dunnere snaar te kiezen.
Het geluid van de snaar is op zichzelf niet goed hoorbaar, maar kan versterkt worden met een klankkast. Dit is een holle ruimte waarin lucht kan gaan meetrillen met de snaren (zie de onderstaande afbeelding).

 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 De geluidsnelheid
In deze paragraaf gaan we rekenen met de golfsnelheid.
Voor de snelheid van een golf gebruiken we de formule voor de snelheid uit het hoofdstuk "Beweging":
$$ v_{geluid} = \frac{s}{t} $$vgeluid staat voor de geluidsnelheid. In BINAS kan je voor een aantal stoffen de geluidsnelheid vinden. De meeste geluidsnelheden zijn hier gegeven bij een temperatuur van 293 K. Dit komt overeen met 293 - 273 = 20 graden Celsius. Voor ijs is de geluidsnelheid bij 269 K gegeven (-4 graden Celsius) en voor lucht is de geluidsnelheid gegeven bij zowel 293 K (20 graden Celsius) als 288 K (15 graden Celsius).
 Voorbeeld
Voorbeeld
|
|
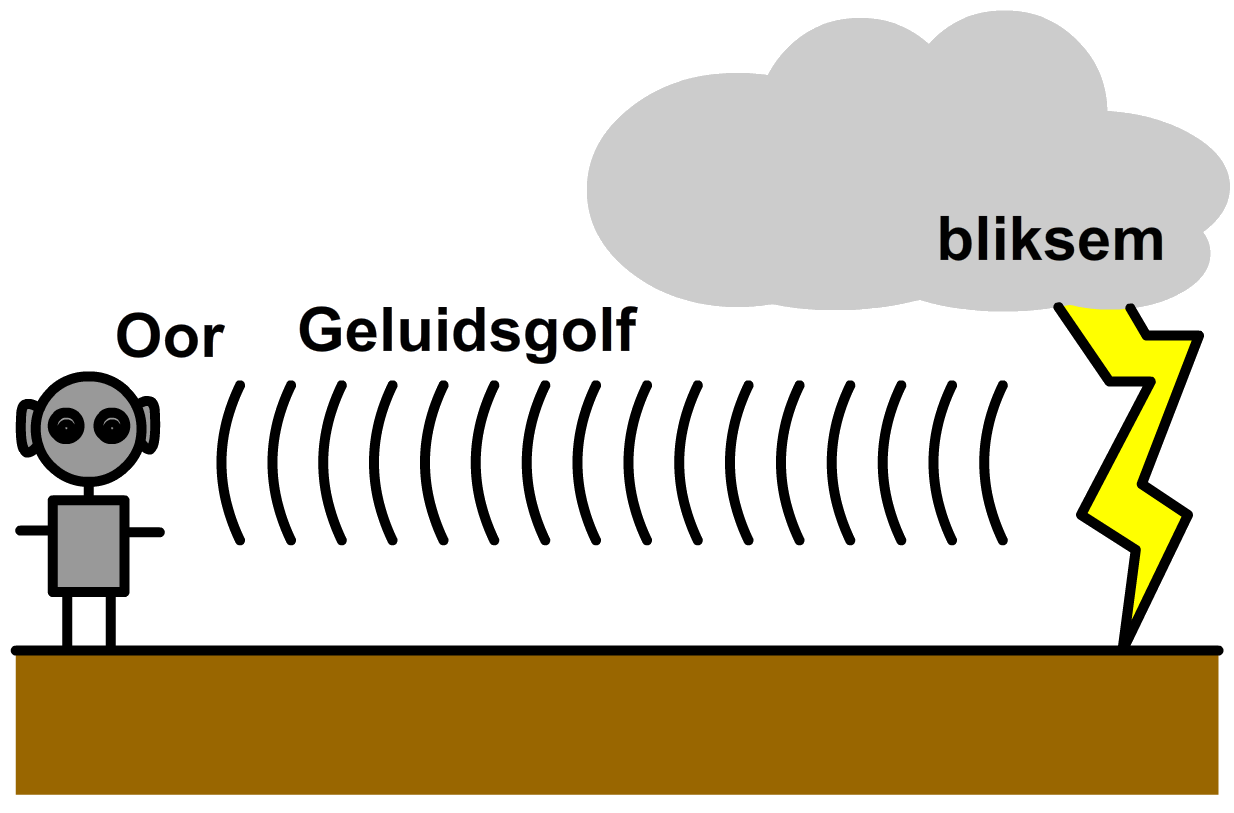
Vraag: Je ziet tijdens een hevige storm een bliksemflits. 8 seconden later hoor je de bijbehorende knal. Bereken hoe ver de bliksem van je vandaan was. De temperatuur van de lucht is 20 oC.
Antwoord: Eerst noteren we de gegevens: t = 8 s 20 graden Celsius komt overeen met 20 + 273 = 293 K. Volgens BINAS geldt voor lucht van 293 K: vgeluid = 343 m/s (BINAS) Nu kiezen we de juiste formule en vullen deze in: $$ s = v_{geluid} \times t $$ $$ s = 343 \times 8 = 2744 \text{ m} $$De bliksem vond dus op een afstand van 2744 meter plaats.
|
In het volgende voorbeeld gaan we redeneren met het begrip echo. Zoals je waarschijnlijk wel weet is een echo een reflectie van geluid tegen een oppervlak.
 Voorbeeld
Voorbeeld
|
|
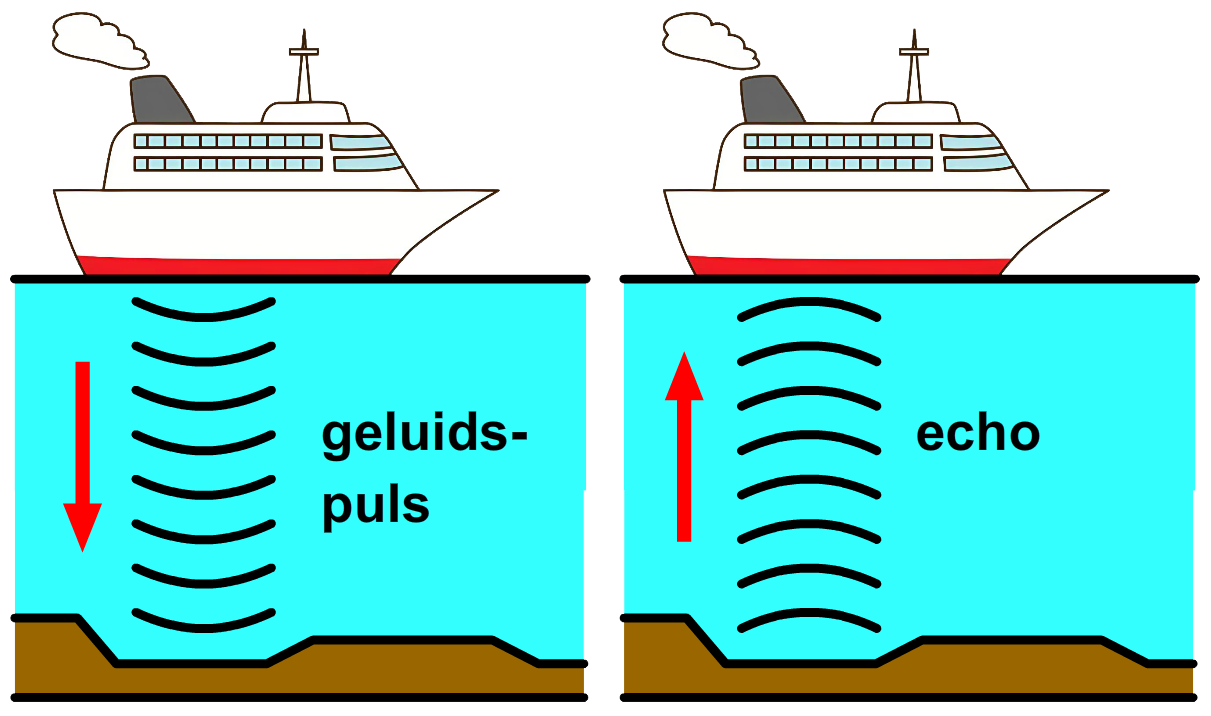
Vraag: Met behulp van echo kan men bepalen hoe diep de zeebodem is. Men stuurt aan de onderkant van een schip een geluidspuls naar beneden en meet hoelang het duurt voordat de puls tegen de bodem reflecteert en terugkomt bij het schip. De puls doet er 0,59 s over om terug te komen bij het schip. Bereken hoe diep de zeebodem is.
Antwoord: Het geluid beweegt eerst naar de zeebodem en daarna weer terug. Dit duurt 0,59 s. We willen weten hoelang het geluid erover doet om alleen de weg naar beneden af te leggen. Hiervoor delen we door twee: t = 0,59 / 2 = 0,295 s Volgens BINAS geldt voor zeewater: vgeluid = 1510 m/s (BINAS) Nu kiezen we de juiste formule en vullen deze in: $$ s = v_{geluid} \times t $$ $$ s = 1510 \times 0,295 = 445 \text{ m} $$De zeebodem is dus 445 meter diep.
|
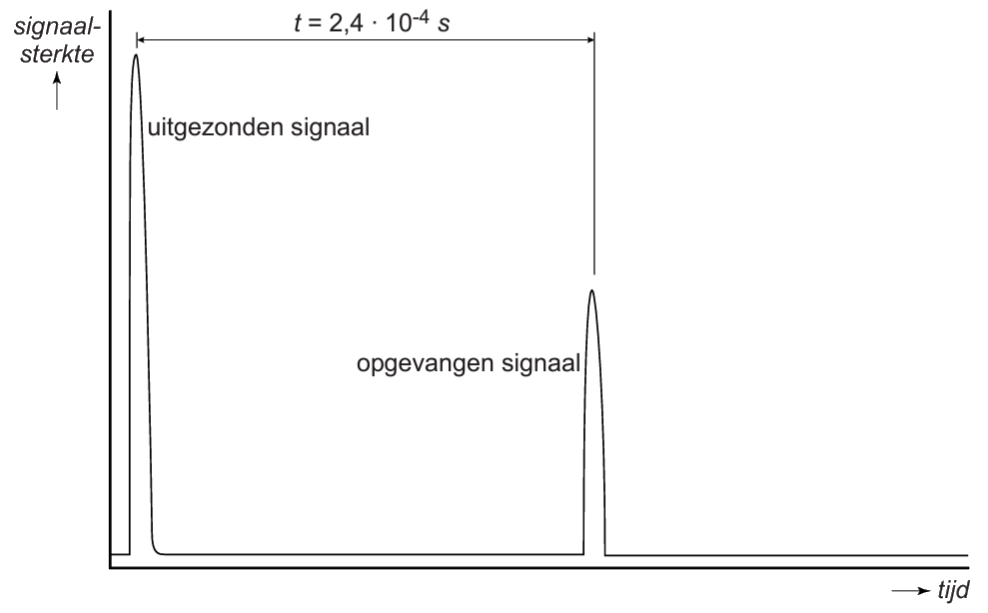
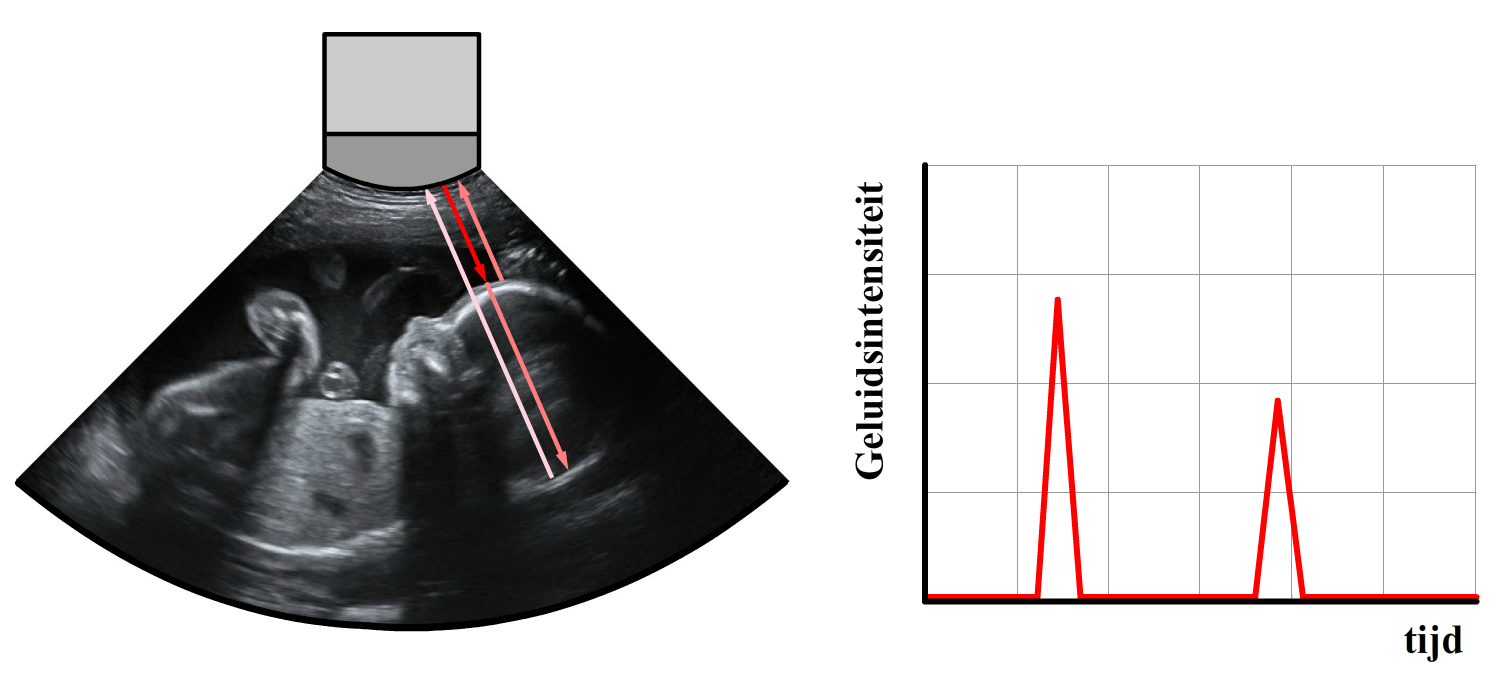
Bij echoscopie wordt ook gebruik gemaakt van echo. Hieronder zien we bijvoorbeeld een echo van een foetus (een baby in de buik van een zwangere vrouw). Deze foto's worden gemaakt door met een speaker korte geluidspulsen de buik van een zwangere vrouw in te sturen. Dit geluid is ultrasoon. Dit betekent dat het geluid is boven de menselijke gehoorgrens. We kunnen dit geluid dus niet horen. Een deel van deze geluidsgolven reflecteert tegen de foetus en komt daarna aan bij een microfoon. In de onderstaande linker afbeelding zien we geluid dat reflecteert tegen de voor en achterkant van de schedel van een foetus. In het rechter diagram zie we het geluid dat terugkomt bij de microfoon. De eerste piek geeft aan wanneer het geluid tegen de voorkant van de baby terugkomt. De tweede piek geeft aan wanneer het geluid tegen de achterkant van de baby terugkomt. Door te meten hoe lang het duurt voordat de verschillende pulsen terugkomen, kan een beeld worden gemaakt van de foetus.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§5 Geluidshinder
In deze paragraaf bespreken we de geluidsterkte. We gaan het ook hebben over geluidshinder en oplossingen daarvoor.
Geluidsterkte meten we met een decibelmeter (dB-meter). Hoe harder het geluid, hoe hoger het aantal decibels (dB). Hoe hard geluid daadwerkelijk klinkt voor het menselijk oor hangt niet alleen af van de hoeveelheid decibel, maar ook van de frequentie van het geluid. Dit komt omdat het oor niet voor alle frequenties even gevoelig is. Zowel erg lage als erg hoge tonen horen we minder hard. Hier wordt rekening mee gehouden bij de zogenaamde dB(A)-schaal.
Hieronder kan je een tabel vinden waarin het effect van geluid bij verschillende dB(A) beschreven staat. Deze tabel kan je ook in BINAS vinden. We zien hier dat 0 dB(A) de gehoordrempel wordt genoemd. Dit is de laagste geluidsterkte die we kunnen horen. Bij 135 dB(A) wordt de pijngrens bereikt. Dit is geluid zo hard dat het pijn doet en levert permanente gehoorschade op. We zien ook dat geluid vanaf 85 dB gehoorbeschadiging kan veroorzaken. Tussen de 85 en de 95 dB gebeurt dit echter pas na 8 uur aanhoren van dit geluid. Bij hogere dB neemt de kans op gehoorschade steeds meer toe.
|
Geluidniveau (dB(A)) |
Zone |
|
|
0 |
Veilig |
Gehoordrempel |
|
10 |
Veilig |
Net hoorbaar |
|
30 |
Veilig |
Erg stil |
|
40 |
Veilig |
Stil |
|
50 |
Veilig |
Rustig |
|
60 |
Veilig |
Indringend |
|
70 |
Veilig |
Storend bij telefoneren |
|
80 |
Veilig |
Hinderlijk |
|
85 |
Kans op gehoorbeschadiging |
Zeer hinderlijk; |
|
95 |
Toenemende kans op gehoorbeschadiging |
Zeer luid |
|
110 |
Permanente gehoorbeschadiging |
Extreem luid |
|
135 |
Permanente gehoorbeschadiging |
Pijngrens |
Er is ook een tabel in BINAS waar je kan vinden hoe lang je veilig naar geluid kan luisteren bij verschillende decibels en een tabel waar de gehoorgevoeligheid bij verschillende leeftijden wordt vergeleken.In een filmpje bij deze paragraaf worden deze tabellen bekeken. Af en toe moet je deze tabellen gebruiken bij het beantwoorden van vragen.
Ook geldt dat we als mens niet alle frequenties kunnen horen. We kunnen alleen frequenties horen tussen de 20 Hz en 20 000 Hz = 20 kHz. Dit zijn de gehoorgrenzen. Geluid onder de 20 Hz en boven de 20 000 Hz kan je dus niet horen. Het is belangrijk dat je de gehoorgrenzen uit je hoofd kent.
In het dagelijks leven worden veel maatregelen genomen om geluidshinder en gehoorschade te voorkomen. Mensen die naast een drukke snelweg wonen ervaren bijvoorbeeld hinder van het geluid van de auto’s die voorbij komen. Dit kan worden verminderd door een geluidsscherm of geluidswal naast de weg te plaatsen (zie de linker onderstaande afbeelding). Deze schermen reflecteren en absorberen een deel van het geluid. Nog twee voorbeelden. Mensen die werken met zware boormachines, die dragen bijvoorbeeld gehoorbeschermers (zie de middelste afbeelding) en als je een podcast wilt opnemen, maar je wil niet dat je stem weergalmt tegen de muren, dan plak je bijvoorbeeld schuimpanelen op de muur (zie de rechter afbeelding). Deze platen absorberen geluid.


 (Afbeelding: Henkiedenkie; CC BY-SA 3.0 / ...)
(Afbeelding: Henkiedenkie; CC BY-SA 3.0 / ...)
Geluid kan worden verminderd bij de bron, onderweg naar de ontvanger of bij de ontvanger. Om geluid bij de bron te verminderen moeten we ervoor zorgen dat de bron minder geluid maakt. Denk bijvoorbeeld aan het ontwikkelen van een koelkast die minder zoemt of een automotor die minder herrie maakt. Bij het verminderen van geluid dat onderweg is naar de ontvanger kan je bijvoorbeeld denken aan de geluidschermen langs de weg. Bij het verminderen van geluid bij de ontvanger kan je denken aan oordoppen bij een concert of de gehoorbeschermers uit de vorige afbeelding.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§5 Rekenen met geluidssterkte
In deze paragraaf gaan we leren rekenen met de geluidsterkte.
Rekenen met decibel (dB) gaat anders dan je gewend bent bij andere eenheden. Stel dat één trompetspeler een geluid maakt van 50 dB. Als we er dan nog een trompetspeler naast zetten die hetzelfde geluid maakt, dan meten we 50 + 3 = 53 dB. Bij het verdubbelen van de geluidsenergie hebben we dus te maken met een stijging van maar 3 dB. Als we weer verdubbelen, nu naar vier trompetspelers, dan wordt de geluidsterkte 53 + 3 = 56 dB.
 Voorbeeld
Voorbeeld
|
|
Vraag: Vier trompetspelers produceren samen een toon met een geluidsterkte van 70 dB. Hoeveel trompetspelers heb je nodig om een geluid van 82 dB te produceren? Ga ervan uit dat de trompetspelers allemaal op gelijke afstand staan en hetzelfde geluid produceren. Antwoord: Elke verdubbeling van het aantal trompetspelers komt overeen met een stijging van 3 dB. In dit geval is de geluidsterkte gestegen met 82 - 70 = 12 dB. Hiervoor moeten we het aantal trompetspelers 12 / 3 = 4 keer verdubbelen. Dit doen we als volgt: $$ 4 \times 2 \times 2 \times 2 \times 2 = 64 $$We hebben dan dus met 64 trompetspelers te maken!
|
 Voorbeeld
Voorbeeld
|
|
Vraag: Vijf trompetspelers produceren samen een toon met een geluidsterkte van 70 dB. Hoeveel decibel meet je bij 80 trompetspelers? Antwoord: We starten met 5 trompetspelers en blijven dit verdubbelen tot we bij 80 trompetspelers uitkomen: $$ 5 \times 2 \times 2 \times 2 \times 2 = 80 $$Zoals je ziet hebben we het aantal trompetspelers vier keer moeten verdubbelen. Elke keer komt er 3 dB bij. We vinden hiermee een geluidsterkte van: $$ 70 \text{ dB} + 3 + 3 + 3 + 3 = 82 \text{ dB} $$
|
 Voorbeeld
Voorbeeld
|
|
Vraag: Een leerling gebruikt bij een concert oordopjes om geen gehoorschade op te lopen. Hierdoor neemt de geluidsterkte 15 dB af. Bereken hoeveel keer het geluid hierdoor wordt verzwakt. Antwoord: Bij elke afname van 3 dB halveert de hoeveelheid geluid. Omdat de geluidsterkte 15 dB afneemt, weten we dat het geluid 15 / 3 = 5 keer is gehalveerd. Het geluid verzwakt dan 2 × 2 × 2 × 2 × 2 = 32 keer.
|
Voor de geluidssterkte geldt ook de volgende regel. Voor elke verdubbeling van de afstand tot een geluidsbron neemt de geluidssterkte met 6 dB af. Het is niet nodig deze regel uit je hoofd te kennen. Als je de regel nodig hebt, zal hij altijd worden gegeven in de vraag.
 Voorbeeld
Voorbeeld
|
|
Vraag: Een leerling is aanwezig bij een concert. Het publiek op de voorste rij staat op een afstand van 8 meter van de luidspreker. De geluidssterkte op deze afstand is 79 dB. Het publiek op de achterste rij zit op een afstand van 32 meter van de luidspreker. Bereken de geluidssterkte in dB op deze afstand. Gebruik hierbij dat bij elke verdubbeling van de afstand de geluidsterkte 6 dB afneemt. Antwoord: We starten met 8 meter en blijven dit verdubbelen tot we bij 32 meter uitkomen: $$ 8 \times 2 \times 2 = 32 \text{ m} $$Zoals je ziet hebben we twee keer moeten verdubbelen. Elke keer neemt de geluidsterkte met 6 dB af. We vinden hiermee een geluidsterkte van: $$ 79 \text{ dB} - 6 - 6 = 67 \text{ dB} $$
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
| BINAS: | |
| 7-12 | Formules |
| 27 | Geluidsnelheden |
| 28 | Gehoorgevoeligheid |
| 29 | Veroudering gehoorgevoeligheid |
| 30 | Maximale blootstelling geluid |