Hoofdstuk 9
Deeltjesmodel
Dit hoofdstuk is voor het VWO alleen onderdeel van het schoolexamen, maar niet van het centraal examen. Voor de HAVO is het wel onderdeel van het centraal examen.
§1 Temperatuur §2 Warmtetransport §3 Soortelijke warmte §4 Geleidbaarheid §5 Debiet (HAVO) §6 Druk (VWO) §7 De ideale gaswet (VWO)
§1 Temperatuur
In dit hoofdstuk gaan we een aantal materiaaleigenschappen begrijpen aan de hand van de deeltjes waaruit deze materialen bestaan. We noemen dit het deeltjesmodel. De fenomenen die aan de hand van dit model gaan verklaren zijn o.a. faseovergangen, temperatuur en druk. In de paragraaf beginnen we met het beschrijven van temperatuur en warmte.
Veel fenomenen in de wereld om ons heen zijn te verklaren aan de hand van de beweging van de atomen waaruit materie is opgebouwd. We noemen deze methode om de wereld te begrijpen het deeltjesmodel. Neem bijvoorbeeld de temperatuur. De temperatuur wordt veroorzaakt door de beweging van de deeltjes waaruit het materiaal bestaat. Hoe sneller de atomen in een voorwerp bewegen, hoe hoger de temperatuur.
 Demonstratievideo
Demonstratievideo
| ||
|
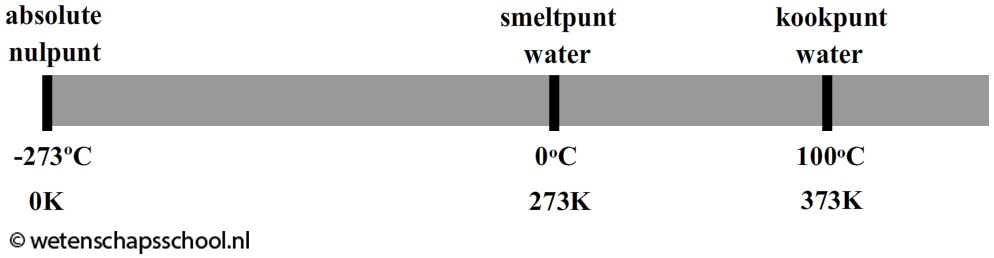
Andersom geldt ook dat hoe langzamer de atomen bewegen, hoe lager de temperatuur wordt. Als we een voorwerp blijven afkoelen, dan komt er een moment dat alle atomen stil staan. Dit gebeurt bij -273 °C. Op dat moment is de allerlaagste temperatuur bereikt. We noemen deze temperatuur het absolute nulpunt. Het is niet mogelijk dat een materiaal nog kouder wordt, want de atomen staan op dit moment immers al helemaal stil.
Sinds de ontdekking van het absolute nulpunt gebruiken we ook vaak de eenheid kelvin (K) voor de temperatuur. Het absolute nulpunt is bij deze schaal gelijkgesteld aan 0 K. Er geldt dus:
| $$ 0 \text{ K} = -273\,^{\circ}\text{C} $$ |
Het handige van deze schaal is dat de temperatuur in kelvin altijd positief is. Het kan immers niet kouder worden dan 0 K. Een ander voordeel is dat formules vaak simpeler worden als we gebruik maken van kelvin. Om deze redenen is de kelvin de SI-eenheid voor de temperatuur. We rekenen kelvin en graden Celsius als volgt in elkaar om:
| $$ T(K) = T(\,^{\circ}\mathrm{C}) + 273 $$ |
T(K) staat voor de temperatuur in kelvin. T(°C) staat voor de temperatuur in graden Celsius.
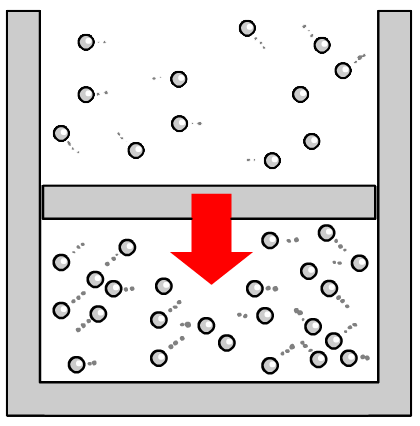
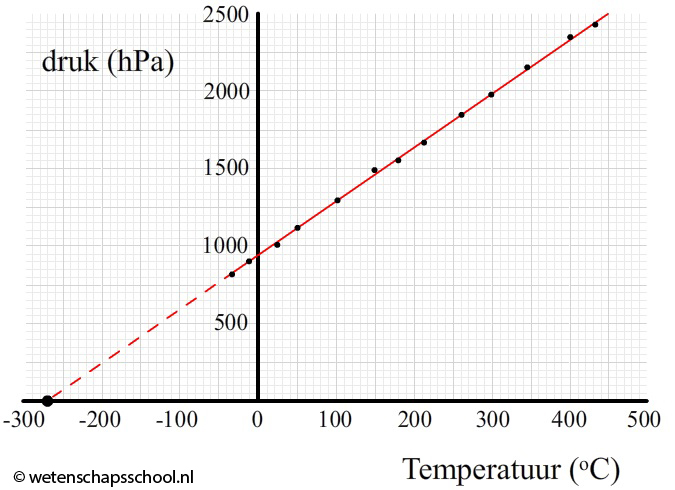
In de onderstaande afbeelding (en het onderstaande filmpje) zien we hoe we de temperatuur behorende bij het absolute nulpunt kunnen vinden met een simpel experiment. Door de temperatuur en de druk van een gas bij verschillende temperaturen te meten krijgen we meetpunten die in een (temperatuur,druk)-diagram mooi op een rechte lijn liggen. Als we deze lijn doortrekken kunnen we de temperatuur vinden bij een druk gelijk aan nul. Als het gas geen druk uitoefent, dan staan de deeltjes stil (ze botsen immers niet meer). De temperatuur die hierbij hoort is het absolute nulpunt.
 Demonstratievideo
Demonstratievideo
| ||
|
Met het deeltjesmodel kunnen we ook meteen begrijpen waarom stoffen uitzetten als we de temperatuur verhogen en krimpen als we de temperatuur verlagen. Als we de temperatuur van bijvoorbeeld een stuk metaal verhogen, dan gaan de deeltjes in dit metaal sneller trillen. Door dit trillen duwt elke atoom de omliggende atomen een beetje weg. Het materiaal neemt op deze manier meer ruimte in (zie de onderstaande animatie). Dit principe wordt bijvoorbeeld gebruikt in een traditionele thermometer. Een veelgebruikte thermometer bestaat uit een dun buisje met daarin gekleurde alcohol. Als de alcohol warmer wordt, dan zet het uit, waardoor het alcoholniveau stijgt. Als de alcohol afkoelt, dan krimpt het, waardoor het alcoholniveau weer daalt.
In veel praktische situaties moeten we rekening houden met deze uitzetting. Bij veel bruggen zien we bijvoorbeeld een "ritssluiting" (zie de linker onderstaande afbeelding). Dit zorgt ervoor dat de brug ruimte heeft om een beetje uit te zetten op een warme dag. In de rechter afbeelding zien we wat er gebeurt als er niet goed wordt nagedacht over de uitzetting van materialen. De rails in de afbeelding zijn helemaal kromgetrokken door het uitzetten.

 (Afbeelding: Matt H. Wade; CC BY-SA 3.0 / PD)
(Afbeelding: Matt H. Wade; CC BY-SA 3.0 / PD)
Bij gassen kan je krimpen en uitzetten nog duidelijker zien. Als je een ballon met daarin lucht koud maakt door het bijvoorbeeld onder te dompelen in vloeibare stikstof, dan zie je de ballon duidelijk krimpen (zie het onderstaande filmpje en de onderstaande afbeeldingen). Als je de ballon daarna weer opwarmt, dan zet de ballon weer uit.

 Demonstratievideo
Demonstratievideo
|
|
In het onderstaande filmpjes zien we dit effect in de praktijk: |
Ook de drie fasen van stoffen kunnen we met het deeltjesmodel begrijpen. In de onderstaande linker afbeelding is een vaste stof afgebeeld. De deeltjes zitten hier op een vaste plaats en kunnen op deze plaats alleen een beetje heen en weer trillen. Alleen bij 0 K staan de deeltjes helemaal stil. Bij een vloeistof zitten de deeltjes nog steeds tegen elkaar aan, maar hebben ze geen vaste plek meer. Ze kunnen nu vrij langs elkaar heen bewegen (zie de middelste afbeelding). Dit verklaart de beweeglijkheid van vloeistoffen. In een gas zijn de deeltjes helemaal los van elkaar en vliegen kriskras door elkaar heen (zie de rechter afbeelding). Een kleurloos gas kan je niet zien. Een voorbeeld hiervan is lucht. De individuele deeltjes zijn immers te klein om met het oog waar te kunnen nemen.
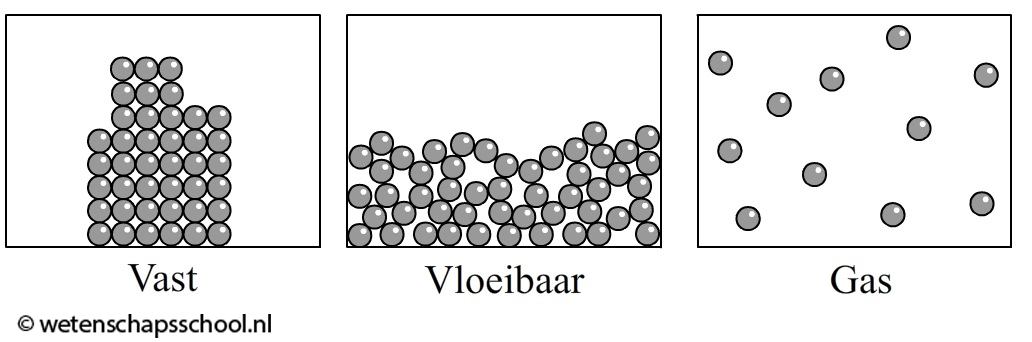
In het onderstaande filmpje worden de drie fasen gemodelleerd met kleine balletjes die in trilling worden gebracht. Ook wordt hier gedemonstreert waarom je een gas gemakkelijk kan indrukken.
 Demonstratievideo
Demonstratievideo
| ||
|
Als een stof van één fase overgaat naar een andere, dan spreken we van een faseovergang. In de onderstaande afbeelding "zien" we water verdampen. Dit is een overgang van vloeibaar naar gas. Let er hier op dat de nevel die boven het kokende water te zien is, bestaat uit kleine druppels in vloeibare fase. Pas als deze druppels lijken te verdwijnen "in het niets", veranderen ze in een gas (genaamd waterdamp). Dit gas kunnen we niet zien.
 (Afbeelding: Pixabay; PD-mod)
(Afbeelding: Pixabay; PD-mod)
Er bestaan zes verschillende faseovergangen. De namen van deze overgangen kan je vinden in de onderstaande afbeelding:
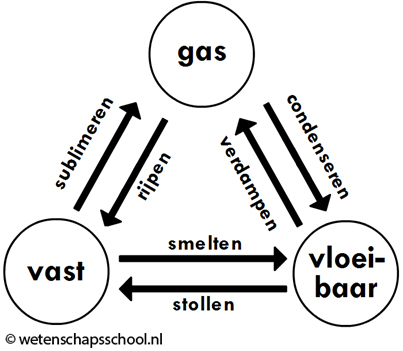
Als een vloeistof in een vaste stof verandert, dan noemen we dit stollen (het stollen van water noemen we ook wel bevriezen). Als een vaste stof in een vloeistof verandert, dan noemen we dit smelten.
Als een vloeistof in een gas verandert, dan noemen we dit verdampen. Als een gas in een vloeistof verandert, dan noemen we dit condenseren (of condensatie). Condensatie treedt bijvoorbeeld op in de linker onderstaande afbeelding. Waterdamp in de lucht komt in aanraking met een koude fles en condenseert tot waterdruppeltjes aan de buitenkant van de fles. Ook dauw en mist ontstaan door condensatie (zie de twee rechter afbeeldingen).


 (Afbeelding: Acdx; CC BY-SA 3.0 / Taro Taylor; CC BY 2.0 / Hillebrand Steve; PD)
(Afbeelding: Acdx; CC BY-SA 3.0 / Taro Taylor; CC BY 2.0 / Hillebrand Steve; PD)
Als een gas in een vaste stof verandert, dan noemen we dit rijpen. Als het in de winter vriest, dan kan de waterdamp uit de lucht direct bevriezen. Bij het rijpen van water ontstaan kleine ijskristalletjes (zie de onderstaande afbeeldingen). De ijskristallen in de vrieskist zijn ook door rijpen ontstaan.

 (Afbeelding: Robert Reisman; CC BY 3.0 / Rubelson; CC BY-SA 4.0)
(Afbeelding: Robert Reisman; CC BY 3.0 / Rubelson; CC BY-SA 4.0)
Als een vaste stof in een gas verandert, dan noemen we dit sublimeren. Tijdens droge winterdagen zien we soms sneeuw verdwijnen, terwijl het de hele dag heeft gevroren. Sneeuw is in dat geval gesublimeerd tot waterdamp. CO2 in vaste vorm, genaamd droogijs, sublimeert ook bij kamertemperatuur.
Ook faseovergangen kunnen we met behulp van deeltjes beschrijven. Als we een vaste stof verwarmen, dan gaan de deeltjes steeds harder trillen. Als het smeltpunt bereikt is, dan trillen de deeltjes zo hard dat ze niet meer op hun vaste plek kunnen blijven zitten. Hoewel de deeltjes nog steeds dicht tegen elkaar aan liggen, beginnen ze nu langs elkaar te bewegen. Als dit gebeurt, is het materiaal aan het smelten en ontstaat er een vloeistof (zie de linker onderstaande afbeelding). Als we de stof nog verder verwarmen, dan bereiken we op een gegeven moment het kookpunt. Bij het kookpunt bewegen de deeltjes zo snel dat ze ontsnappen uit de vloeistof. Als dit gebeurt, is het materiaal aan het verdampen en ontstaat er een gas (zie de middelste afbeelding).
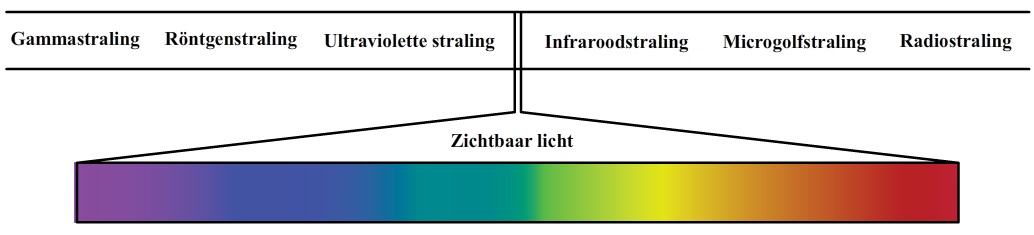
Ook het gloeien van materie kunnen we begrijpen met behulp van het trillen van deeltjes. Materie bestaat voor een groot deel uit geladen deeltjes (protonen en elektronen). Als geladen deeltjes trillen, dan produceren ze elektromagnetische straling. Deze golven noemen we ook wel licht. Omdat zo goed als elk materiaal een temperatuur heeft boven de 0 K, kunnen we dus stellen dat zo goed als elk materiaal in het universum straling uitzendt. Meestal zit deze straling echter buiten het zichtbare spectrum en kunnen we dit dus niet zien. De aarde en ook wijzelf zenden bijvoorbeeld voornamelijk infraroodstraling uit. Hieronder zien we het volledige spectrum. Links van het paarse deel van het spectrum bevindt zich ultravioletstraling, röntgenstraling en gammastraling. Rechts van het rode deel van het spectrum hebben we infraroodstraling, microgolfstraling en radiostraling. Zoals je in de onderstaande afbeelding kan zien is het zichtbare deel van het spectrum maar een klein deel van het gehele spectrum.
Als de temperatuur van een voorwerp hoog genoeg is, dan komt er een moment dat de straling wel zichtbaar wordt. Dit zien we bijvoorbeeld in de onderstaande afbeelding. Een stuk metaal is hier sterk verwarmd en begint hierdoor te gloeien in het rode deel van het spectrum.

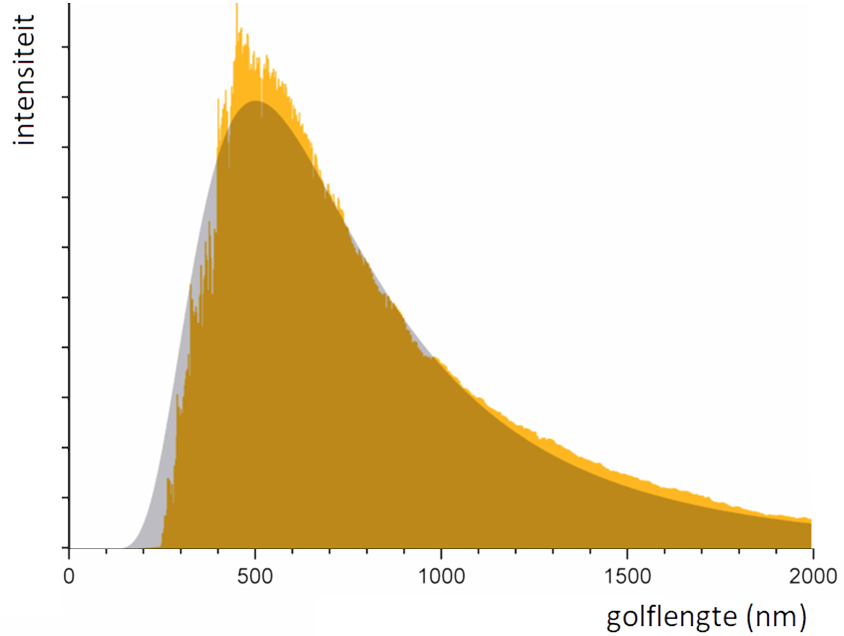
Het licht dat op deze manier ontstaat heeft een karakteristiek stralingsspectrum, genaamd de planckkromme of het planckspectrum (zie de onderstaande afbeelding). De golflengte van de piek van de planckkromme hangt af van de temperatuur volgens de zogenaamde wet van Wien:
$$\lambda_{max} = \frac{k_w}{T}$$
|
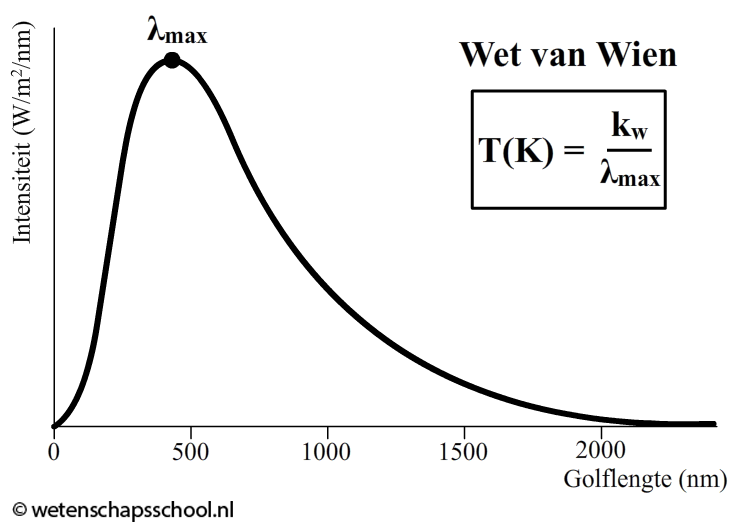
Met de wet van Wien kunnen we bijvoorbeeld de temperatuur van een gloeilamp bepalen of de oppervlaktetemperatuur van de zon. De piek van het stralingsspectrum van onze zon ligt bij de 500 nm. We vinden hiermee:
$$T = \frac{k_w}{\lambda_{max}}$$ $$T = \frac{2,8977721 \times 10^{-3}}{500 \times 10^{-9}} = 5,80 \times 10^3 \text{ K}$$Met behulp van de wet van Wien zien we dat de piek van de stralingskromme naar links opschuift bij hogere temperaturen. Dit is ook te zien in de onderstaande animatie. De regenboog in de grafiek stelt het zichtbare deel van het spectrum voor.
Bij een lage temperatuur zit de straling bijna volledig in het infrarode deel van het spectrum. Als gevolg kunnen we deze straling niet waarnemen met onze ogen. Als de temperatuur hoger wordt, dan komt er een moment dat er genoeg rood licht wordt geproduceerd, zodat we dit met onze ogen kunnen zien. Als we de temperatuur nog meer verhogen, dan komt er een moment dat er in het hele zichtbare spectrum veel licht wordt uitgezonden. Als we alle kleuren licht tegelijk in onze ogen krijgen, dan zien we dit als wit licht. Als de temperatuur nog hoger wordt, dan gaat op een gegeven moment het blauwe licht domineren. Als we stoffen blijven verwarmen, dan gloeien ze dus eerst met rood licht, dan met wit licht en dan met blauw licht. Om dezelfde reden zijn er ook rode, witte en blauwe sterren.
 Voorbeeld
Voorbeeld
|
|
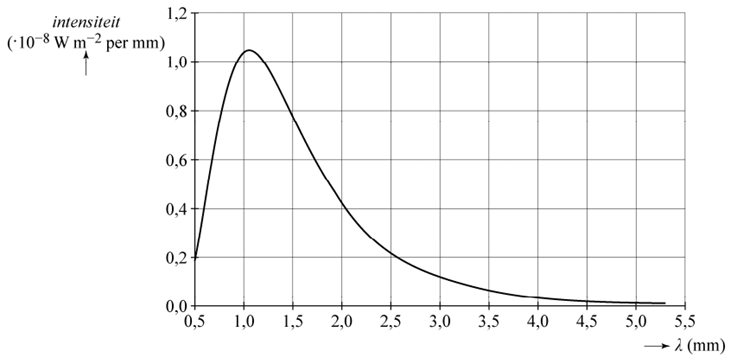
Vraag: Kosmische achtergrondstraling is straling die net na de oerknal is ontstaan. Deze straling kan in het hele heelal gemeten worden. In de onderstaande grafiek is de intensiteit van deze straling uitgezet tegen de golflengte. Bepaal de temperatuur behorende bij de achtergrondstraling.
Antwoord: Het maximum van de grafiek ligt bij λmax= 1,05 nm. Met de wet van Wien vinden we: $$T = \frac{k_w}{\lambda_{max}} = \frac{2,8978 \times 10^{-3}}{1,05 \times 10^{-3}} = 2,76 \text{ K}$$
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§2 Warmtetransport
In deze paragraaf gaan we het hebben over het verschil tussen warmte en temperatuur en gaan we drie manieren bestuderen waarop warmte kan stromen van de ene plek naar de andere.
Als je een kruik vult met heet water en deze tegen je lichaam houdt, dan wordt je lichaam warmer en de kruik langzaam kouder (zie de linker onderstaande afbeelding). En als je een ice pack tegen je lichaam houdt, dan wordt je lichaam kouder en de ice pack juist warmer (zie de rechter afbeelding). In beide gevallen zeggen we dat er warmte is verplaatst van een warme naar een koude stof.
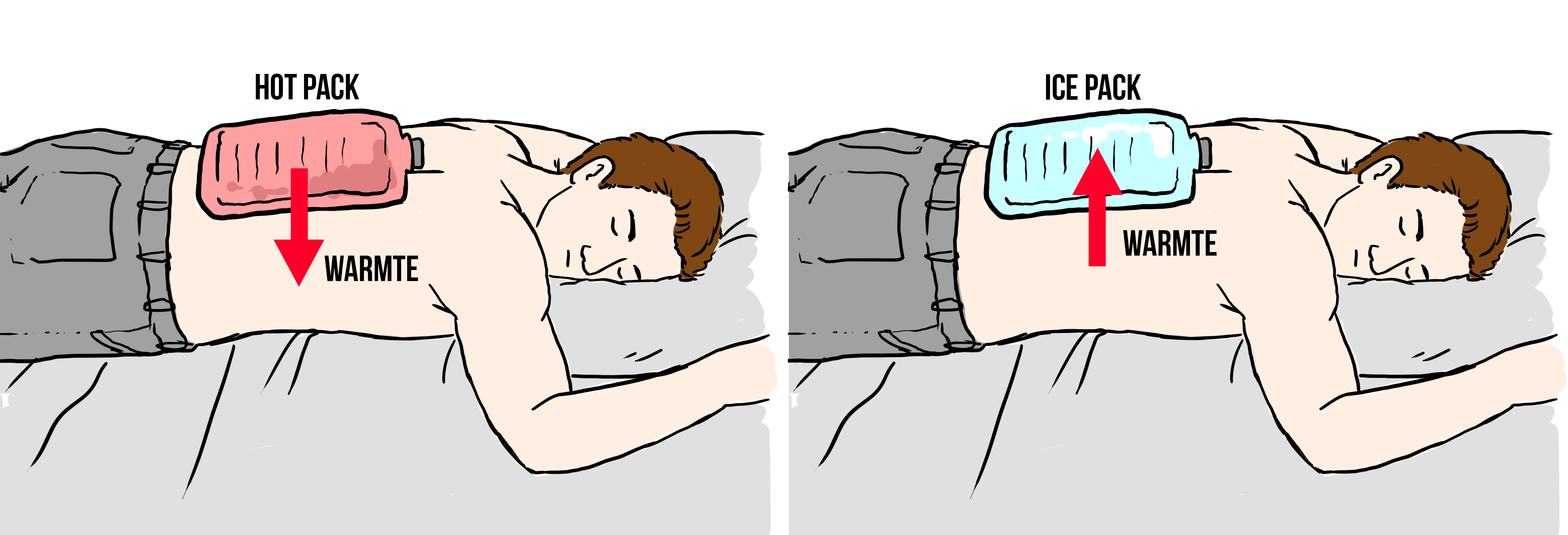
In het dagelijks leven wordt in dit voorbeeld ook wel eens gezegd dat "kou" van een koude naar een warme stof stroomt. In de natuurkunde wordt deze manier van denken echter zo veel mogelijk vermeden. Warmte is namelijk een vorm van energie en deze energie stroomt altijd van warme naar koude voorwerpen. Een zin als "doe het raam dicht, want er komt kou binnen" is natuurkundig gezien dus onhandig. Wat er in werkelijkheid gebeurt is dat er juist warmte naar buiten stroomt.
Het is belangrijk om onderscheid te maken tussen warmte en temperatuur. De temperatuur meten we met een thermometer en de eenheid hiervan is graden Celsius of kelvin. Warmte is een soort energie en de eenheid hiervan is de joule. Er geldt dus:
|
Temperatuur (T) |
kelvin (K) |
|
Energie (E) |
joule (J) |
|
Warmte (Q) |
joule (J) |
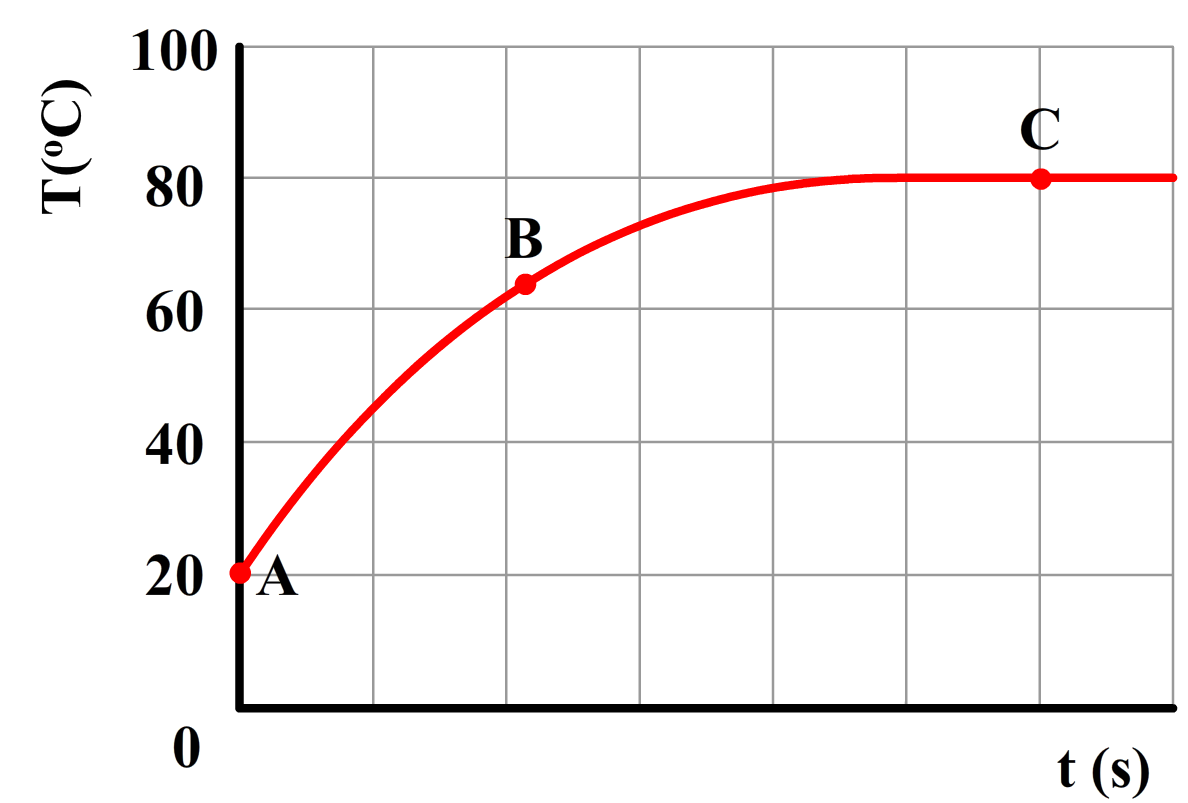
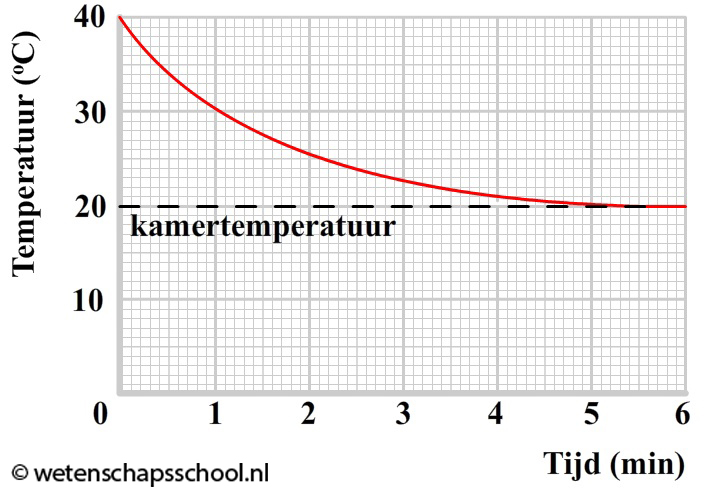
Hoeveel warmte er zal stromen van een plek met hoge temperatuur naar een plek met lage temperatuur hangt af van het temperatuurverschil (ΔT) tussen deze twee plekken. Hoe groter het temperatuurverschil, hoe meer warmte er zal stromen. We kunnen dit goed zien in het onderstaande diagram. Het diagram geeft het afkoelen van een klein voorwerp in een kamer met een temperatuur van 20 graden Celsius weer. Merk op dat bij een groot temperatuurverschil tussen het voorwerp en de kamer, de temperatuur van het voorwerp snel afneemt. Als de temperatuur van het voorwerp na verloop van tijd niet meer zo veel verschilt van de kamertemperatuur, dan neemt de temperatuur nog maar heel langzaam af.
Het stromen van warmte noemen we ook wel warmtetransport. Er bestaan drie soorten warmtetransport:
- Warmtegeleiding
- Warmtestroming
- Straling
We gaan deze drie soorten hieronder uitgebreid bespreken.
Warmtegeleiding:
Warmtegeleiding (ook wel gewoon geleiding genoemd) ontstaat doordat deeltjes hun warmte doorgeven doordat ze tegen elkaar botsen. Stel dat een stuk metaal op één plek wordt verwarmd. Als gevolg gaan op deze plek de deeltjes sneller trillen. Deze deeltjes botsen dan tegen omringende deeltjes en deze worden als gevolg ook in trilling gebracht. Op deze manier trekt de warmte door het materiaal. We zien dit effect bijvoorbeeld als we een metalen lepel in een pan kokend water plaatsen. De warmte trekt dan door het metaal omhoog (zie de onderstaande afbeelding).

 Demonstratievideo
Demonstratievideo
| ||
|
Niet alle stoffen geleiden warmte even goed. Een metalen lepel in een pan met kokend water wordt bijvoorbeeld veel sneller warm dan een houten lepel. Metaal wordt daarom een goede geleider genoemd en hout een slechte geleider. Slechte geleiders worden ook wel isolatoren genoemd.
Niet alle stoffen geleiden warmte even goed. Een metalen lepel in een pan met kokend water wordt bijvoorbeeld veel sneller warm dan een houten lepel. Metaal wordt daarom een goede geleider genoemd en hout een slechte geleider. Slechte geleiders worden ook wel isolatoren genoemd.

Ook gassen en vloeistoffen zijn isolatoren. Een thermosfles maakt bijvoorbeeld gebruik van de isolerende eigenschap van lucht. De wand van een thermosfles bestaat uit twee laagjes met daartussen lucht (zie de onderstaande afbeelding). Doordat lucht slecht geleid, kan de warmte hierdoor lastig de fles in en lastig de fles uit. Warme dranken blijven hierdoor langer warm en koude dranken langer koud. Hetzelfde principe wordt toegepast bij dubbelglas. Dubbelglas bestaat uit twee glazen met daartussen lucht. Dit zorgt ervoor dat we weinig warmte verliezen via de ramen en als gevolg besteden we minder geld aan het opwarmen van ons huis. Ook via de muren ontsnapt warmte. Om dit te verminderen bestaan muren vaak uit twee delen met daartussen lucht. Dit worden ook wel spouwmuren genoemd.

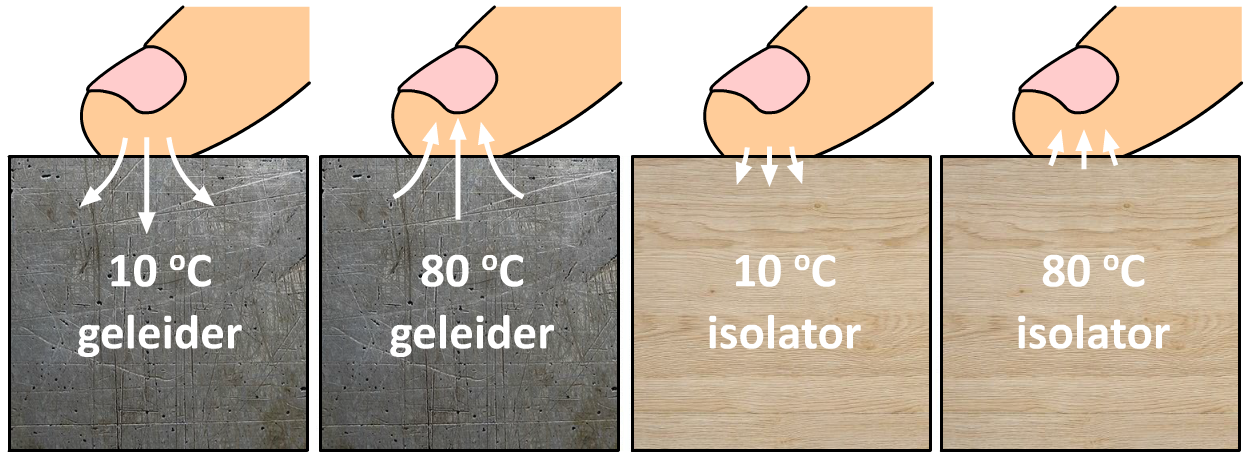
Het verschil in geleidbaarheid van verschillende stoffen kunnen we ook zien in de onderstaande afbeelding. Als je je vinger op een koude geleider legt, dan trekt de warmte van je vinger snel in het materiaal en wordt je vinger koud. Als gevolg zeg je dat het metaal koud aan voelt. Als je je vinger op een hete geleider legt, dan trekt de warmte ook snel je vinger in. Als gevolg voelt het metaal erg heet aan. Bij een isolator is de warmte-overdracht zowel bij lage als hoge temperatuur niet groot. Als gevolg voelt het materiaal niet heel heet en niet heel koud aan. Het verschil in geleidbaarheid verklaart ook waarom je in een sauna lucht van 80 oC aankan, maar je niet in een bak water van 80 oC wilt springen. Doordat lucht een slechtere geleider is, geeft het zijn energie veel lastiger af aan je lichaam.
 Demonstratievideo
Demonstratievideo
| ||
|
Warmtestroming:
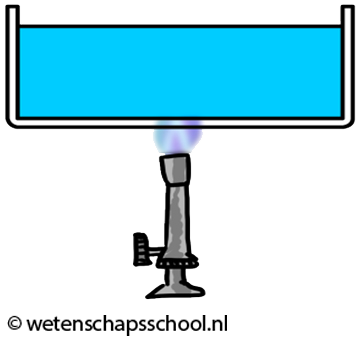
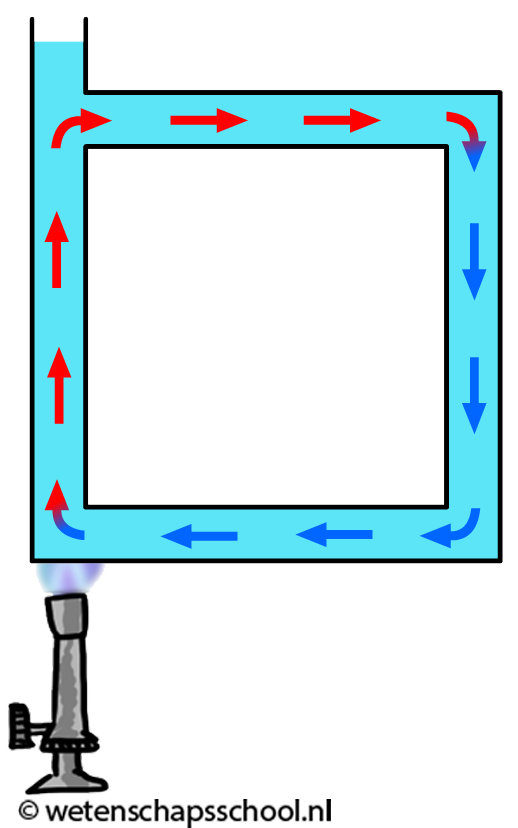
Hoewel gassen en vloeistoffen slechte geleiders zijn, kan warmte in deze materialen wel goed worden getransporteerd met behulp van warmtestroming. We kunnen dit effect goed zien in de onderstaande linker afbeelding. We zien hier dat water in een buis verwarmd wordt. Door geleiding zal het water in de buurt van de vlam opwarmen. Dit warme water zet uit en als gevolg wordt de dichtheid van het water kleiner en zal het opstijgen. Hierdoor begint het water rond te stromen.
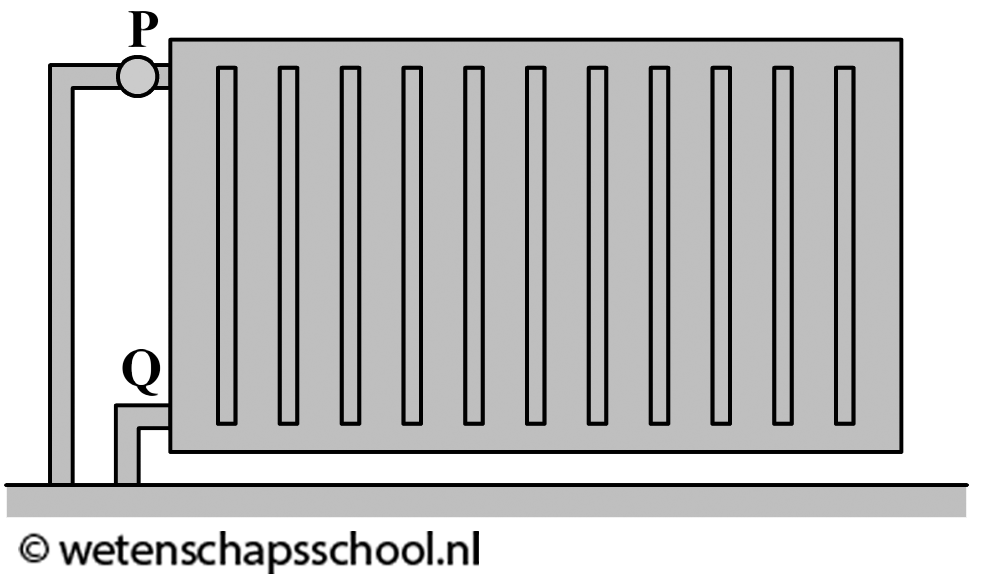
Ook het verwarmen van een kamer gebeurt op deze manier (zie de rechter afbeelding). Een warme verwarming kan met behulp van geleiding alleen de lucht verwarmen die direct in contact staat met de verwarming. Deze lucht wordt hierdoor warmer, krijgt een lagere dichtheid en stijgt op. Als gevolg ontstaat er een warmtestroom in de kamer en wordt de kamer steeds warmer.
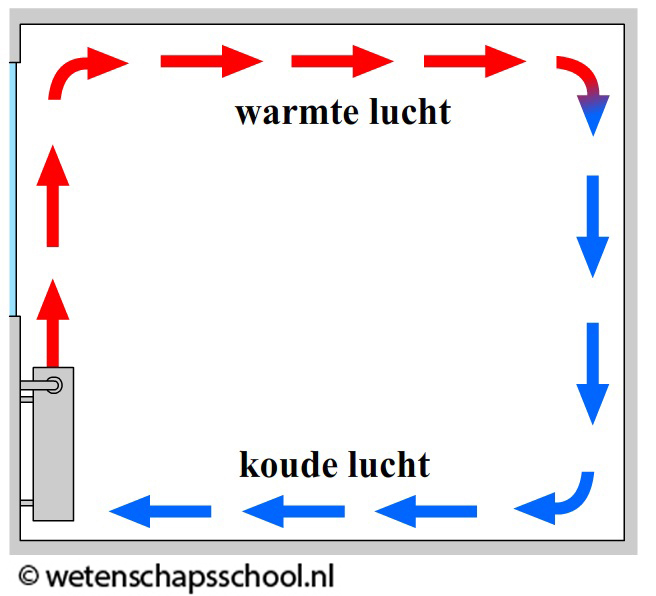
 Demonstratievideo
Demonstratievideo
| ||
|
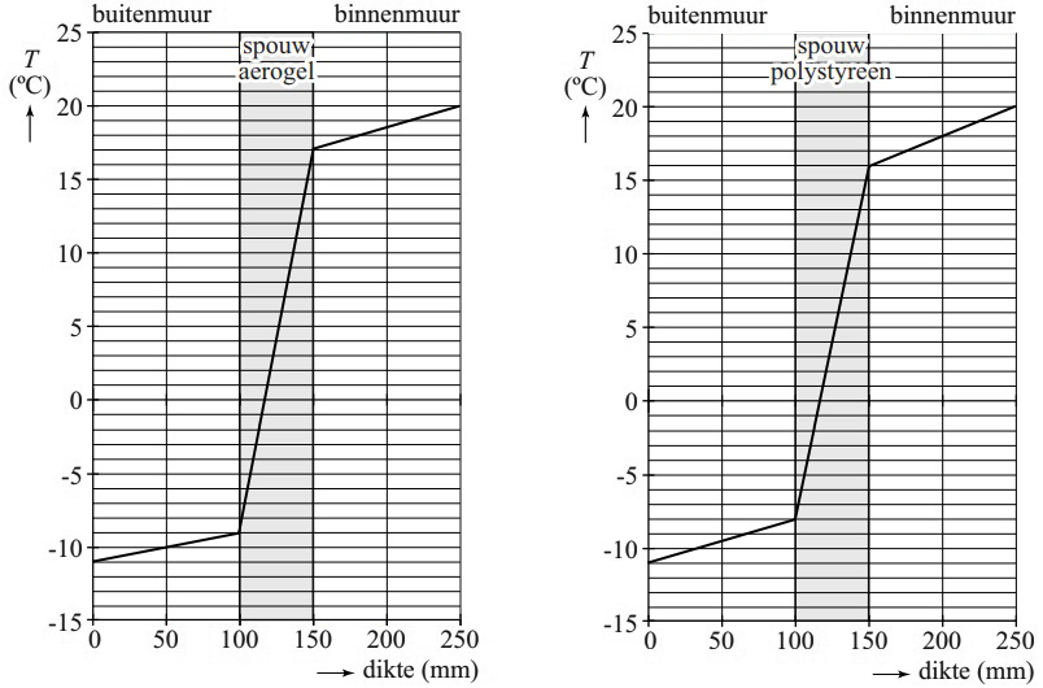
In sommige gevallen willen we warmtestroming juist beperken. Als een huis in de winter verwarmd wordt, dan wordt de binnenwand van de spouwmuur ook warm. Er ontstaat dan tussen de binnen- en de buitenwand warmtestroming van lucht. Op deze manier komt de warmte van de binnenmuur redelijk gemakkelijk bij de buitenmuur aan en daarna ontsnapt de warmte uit het huis. Dit kan worden voorkomen door isolatiemateriaal tussen de wanden te plaatsen. Een voorbeeld hiervan is purschuim of glaswol(zie de onderstaande afbeelding). In beide stoffen zitten belletjes lucht vast in het materiaal. Als gevolg kan geen stroming optreden. De aanwezigheid van lucht beperkt in dat geval geleiding en het isolatiemateriaal zelf beperkt stroming.

Straling:
De derde soort warmtetransport wordt straling genoemd. Een ander woord voor straling is licht. Dat straling warmte kan overdragen weten we als we onze handen in de zon houden. Dit zonlicht wordt dan geabsorbeerd en hierdoor wordt onze huid warmer. Hetzelfde effect treedt ook op als je je handen warmt aan een kampvuur of openhaard (zie de linker onderstaande afbeelding). Er is ook straling die we niet met onze ogen kunnen zien. Alle warme objecten, inclusief ons eigen lichaam, zenden bijvoorbeeld infraroodstraling uit. In de rechter afbeelding zien we een foto van warm water dat uit een kraan stroomt, gemaakt met een infraroodcamera. Zoals je ziet geeft warm water infraroodstraling af. Als je je hand naast een hete verwarming plaatst, dan kan je de infraroodstraling ook voelen (boven de verwarming is het nog warmer, maar dat komt voornamelijk door warmtestroming).

 (Afbeelding: ... / NASA; PD)
(Afbeelding: ... / NASA; PD)
Om verlies via straling tegen te gaan, wordt soms glanzende folie tegen de muur achter een verwarming geplakt (zie de onderstaande afbeelding). De infraroodstraling die van de verwarming afkomt wordt dan terug de kamer in gereflecteerd.

 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§3 Soortelijke warmte
In deze paragraaf gaan we preciezer kijken naar de link tussen warmte en temperatuur. We doen dit met behulp van het begrip soortelijke warmte.
Als we willen weten hoeveel warmte er nodig is om de temperatuur van een vloeistof een bepaalde hoeveelheid te laten stijgen, dan gebruiken we daarvoor een joulemeter (ook wel calorimeter genoemd). Een joulemeter is eigenlijk niets anders dan een geïsoleerd bakje met daarin een verwarmingselement en een thermometer. In de onderstaande afbeelding zien we een joulemeter gevuld met water. In het verwarmingselement wordt elektrische energie omgezet in warmte en met deze warmte wordt het water verwarmd. Hoeveel de temperatuur van het water hierdoor stijgt, kunnen we aflezen op de thermometer.
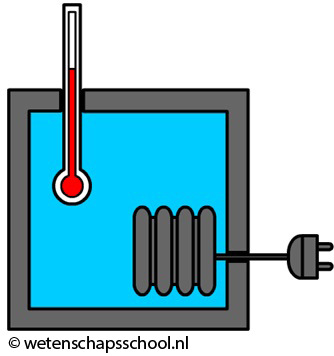
De hoeveelheid elektrische energie die we toevoegen (ΔE) kunnen we uitrekenen met behulp van de spanning en de stroomsterkte. We doen dit met behulp van de volgende twee formules uit het hoofdstuk "Elektriciteit":
$$ P = U \times I $$
$$ \Delta E = P \Delta t $$
|
Met de spanning en de stroomsterkte kunnen we met de eerste formule het vermogen (P) bereken. Met de tweede formule kunnen we met het vermogen de totale elektrische energie uitrekenen. Deze elektrische energie zal in de joulemeter worden omgezet in warmte (Q). Als de joulemeter perfect geïsoleerd is, dan wordt al deze warmte gebruikt om het water op te warmen. Met een thermometer kunnen we dan de temperatuurstijging (ΔT) aflezen. Met de warmte (Q) en de temperatuurstijging (ΔT) kunnen we dan de zogenaamde soortelijke warmte (c) berekenen:
$$ Q = c m \Delta T $$
|
De SI-eenheid voor de temperatuurstijging (ΔT) is kelvin, maar er mag in deze formule ook gebruik gemaakt worden van graden Celsius. Dit komt omdat we hier niet te maken hebben met een temperatuur, maar met een temperatuursverschil. Of we nu te maken hebben met een stijging van 0 °C naar 10 °C of van 273 K naar 283 K, de temperatuurstijging is in beide gevallen 10.
De soortelijke warmte (c) vertelt ons hoeveel warmte er nodig is om één kilogram materiaal één kelvin (of één graden Celsius) te laten stijgen. De SI-eenheid van de soortelijke warmte is dus J/kg/K. Voor een heel aantal stoffen is de soortelijke warmte te vinden in BINAS.
Laten we een paar voorbeelden bespreken. Water heeft een relatief grote soortelijke warmte. Je kan dus relatief veel energie in water opslaan voordat de temperatuur een graad stijgt. Als gevolg is water een goede koelvloeistof. Ditzelfde effect zorgt er ook voor dat Nederland geen extreme hete zomers en koude winters kent. Doordat het veel energie kost om water op te warmen, wordt het in de zomers niet heel heet en omdat water veel energie kwijtraakt bij het afkoelen, wordt het in de winters niet heel koud.
 Demonstratievideo
Demonstratievideo
| ||
|
De formule wordt ook vaak gebruikt in combinatie met de formule voor de dichtheid (m = ρV). We vinden dan:
$$ Q = c \rho V \Delta T $$
|
In werkelijkheid is een joulemeter natuurlijk nooit perfect geïsoleerd. Er zal hierdoor altijd wat warmte ontsnappen. Als gevolg wordt de temperatuur van de vloeistof lager. De fractie van de energie die nuttig gebruikt wordt (en dus niet verloren gaat) noemen we het rendement. Het rendement kunnen we als volgt berekenen:
| $$ \frac{E_{nuttig}}{E_{tot}} = \eta $$ |
Het rendement in deze formule is een getal tussen de 0 en de 1. Het rendement wordt ook vaak uitgedrukt als percentage. In dat geval moet het rendement uit deze formule vermenigvuldigd worden met 100. Een rendement van bijvoorbeeld 0,05 komt dus overeen met een rendement van 5%.
Warmte kan ook ontstaan bij het verbranden van brandstoffen. De energie die bij verbranding vrijkomt, noemen we de chemische energie (Ech). In BINAS kunnen we de stookwaarde (rV) van verschillende brandstoffen vinden. De stookwaarde vertelt ons hoeveel joule er vrijkomt bij het verbranden van een kubieke meter brandstof. De eenheid van de stookwaarde is dus J/m3. Met de stookwaarde kunnen we als volgt de totale chemische energie uitrekenen die bij een verbranding vrijkomt:
$$ E_{ch} = r_VV$$
|
 Voorbeeld
Voorbeeld
|
|
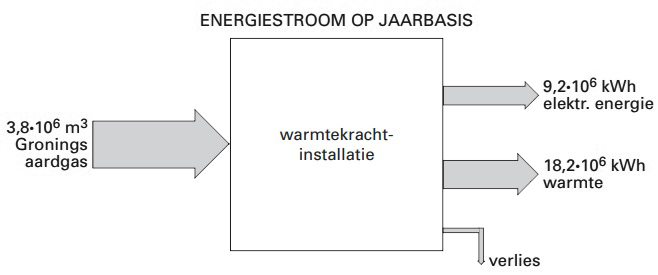
Opdracht: Een persoon wil een kamer van 14,4 oC naar 20,0 oC verwarmen. De kamer heeft een volume van 18 m3. Bereken hoeveel kubieke meter Gronings aardgas er verbrand moet worden voor deze temperatuurstijging. Antwoord: Eerst berekenen we hoeveel warmte je nodig hebt om de lucht in de kamer op te warmen. In BINAS vinden we de volgende gegeven over lucht: c = 1,0 × 103 J/kg/K ρ = 1,29 kg/m3 Het temperatuurverschil (ΔT) van de lucht is gelijk aan: ΔT = 20,0 - 14,4 = 5,6 oC Nu berekenen we de warmte die nodig is om de lucht op te warmen: $$ Q = c \rho V \Delta T = 1,0 \times 10^3 \times 1,29 \times 18 \times 5,6 = 1,3 \times 10^5 \text{ J}$$De warmte wordt geproduceerd door middel van het verbranden van Gronings aardgas. In BINAS vinden we de stookwaarde van Gronings aardgas: rV = 32 × 106 J/m3 Het volume aardgas wordt hiermee: $$ V = \frac{E_{ch}}{r_V} = \frac{1,3 \times 10^5}{32 \times 10^6} = 0,0041 \text{ m}^3 $$Dit is het volume Groningsaardgas dat minimaal verbrandt moet worden. In werkelijkheid ligt de waarde een stuk hoger, omdat er normaal gesproken ook nog warmte ontsnapt, bijvoorbeeld via de ramen van de kamer.
|
Een andere manier om een kamer te verwarmen is met een warmtepomp (zie de onderstaande afbeelding). In de buizen van een warmtepomp wordt een stof met een laag kookpunt, zoals ammoniak, binnenshuis samengeperst van de gasfase naar de vloeistoffase. Bij deze faseovergang komt warmte vrij waarmee het huis verwarmd wordt.
Daarna wordt de vloeistof buiten het huis gepompt. Hier wordt de druk weer verlaagd, zodat de stof weer verdampt tot een gas. Bij deze faseovergang wordt warmte opgenomen uit de omgeving. De omgeving wordt hierdoor kouder. Nu de ammoniak weer in gasvorm is, kan het weer het huis in worden gepompt en kan het proces weer opnieuw beginnen.

 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 Geleidbaarheid
In deze paragraaf bestuderen we het stromen van warmte door een oppervlak, bijvoorbeeld door een raam. We noemen dit de warmtestroom.
Als we een kamer verwarmen, dan verliezen we continu warmte via o.a. de ramen. De warmte die we per seconde verliezen door een oppervlak noemen we de warmtestroom (P). Net als bij het vermogen gebruiken we hiervoor de eenheid watt (W). We kunnen de warmtestroom als volgt berekenen:
$$ P = \lambda A \frac{\Delta T}{d}$$
|
De warmtegeleidingscoëfficiënt (λ) is een stofeigenschap die voor een aantal stoffen in BINAS te vinden is. Hoe groter de warmtegeleidingscoëfficiënt, hoe beter een stof geleid. "ΔT" is nu niet de temperatuurstijging, maar het verschil in temperatuur aan weerzijden van het oppervlak. In het geval van een kamer is dit dus het verschil tussen de binnen- en de buitentemperatuur.
Als we een kamer op constante temperatuur willen houden, dan moet de warmtestroom die de kamer verlaat gelijk zijn aan de warmte die via een verwarming wordt toegevoerd. Met de formule "Ech = rVV" kan dan worden berekend hoeveel aardgas moet worden verbrand om de temperatuur constant te houden.
Het verschil in geleidbaarheid van stoffen merk je bijvoorbeeld als je op een erg koude dag (zeg, -5 oC) een stuk metaal en een stuk hout aanraakt. Hoewel beide voorwerpen dezelfde temperatuur hebben (-5 oC), voelt het metaal toch een stuk kouder uit. Dit komt omdat metaal een stuk beter warmte geleid en dus veel gemakkelijker warmte uit te hand trekt. Als gevolg koelt je hand sneller af (en wordt het metaal sneller warm).
Het is belangrijk goed te begrijpen wanneer je de formule met de soortelijke warmte moet gebruiken en wanneer de formule met de warmtegeleidingscoëfficiënt. Als een stof afkoelt of verwarmt, dan gebruiken we de soortelijke warmte. Denk bijvoorbeeld aan het koken van water in een waterkoker, het afkoelen van een brood in de vriezer of het verwarmen van zand op een zomerse dag. Als warmte door een oppervlak stroomt, dan gebruiken we de warmtegeleidingscoëfficiënt. Denk bijvoorbeeld aan de warmte die door de ramen van een huis naar buiten trekt, de warmte die door het glas van een verwarmde vissenkom ontsnapt of de warmte die door je huid je lichaam ontsnapt.
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§5 Debiet (HAVO)
In deze paragraaf gaan we het stromen van vloeistoffen bestuderen. We doen dit aan de hand van het begrip debiet.
Stel we vullen een zwembad met een tuinslang. Het volume water dat per tijdseenheid uit de slang komt noemen het debiet. Debiet wordt bijvoorbeeld gemeten in m3/s of L/s. De formule voor debiet is:
$$ Q = \frac{\Delta V}{\Delta t}$$
|
We kunnen we formule voor debiet ook herschrijven. Denk aan een hoeveelheid water in een tuinslang. Het volume van het water in de slang kunnen we ook schrijven als de doorsnede (A) keer de lengte (Δx) van de slang:
$$ V = A \times \Delta x $$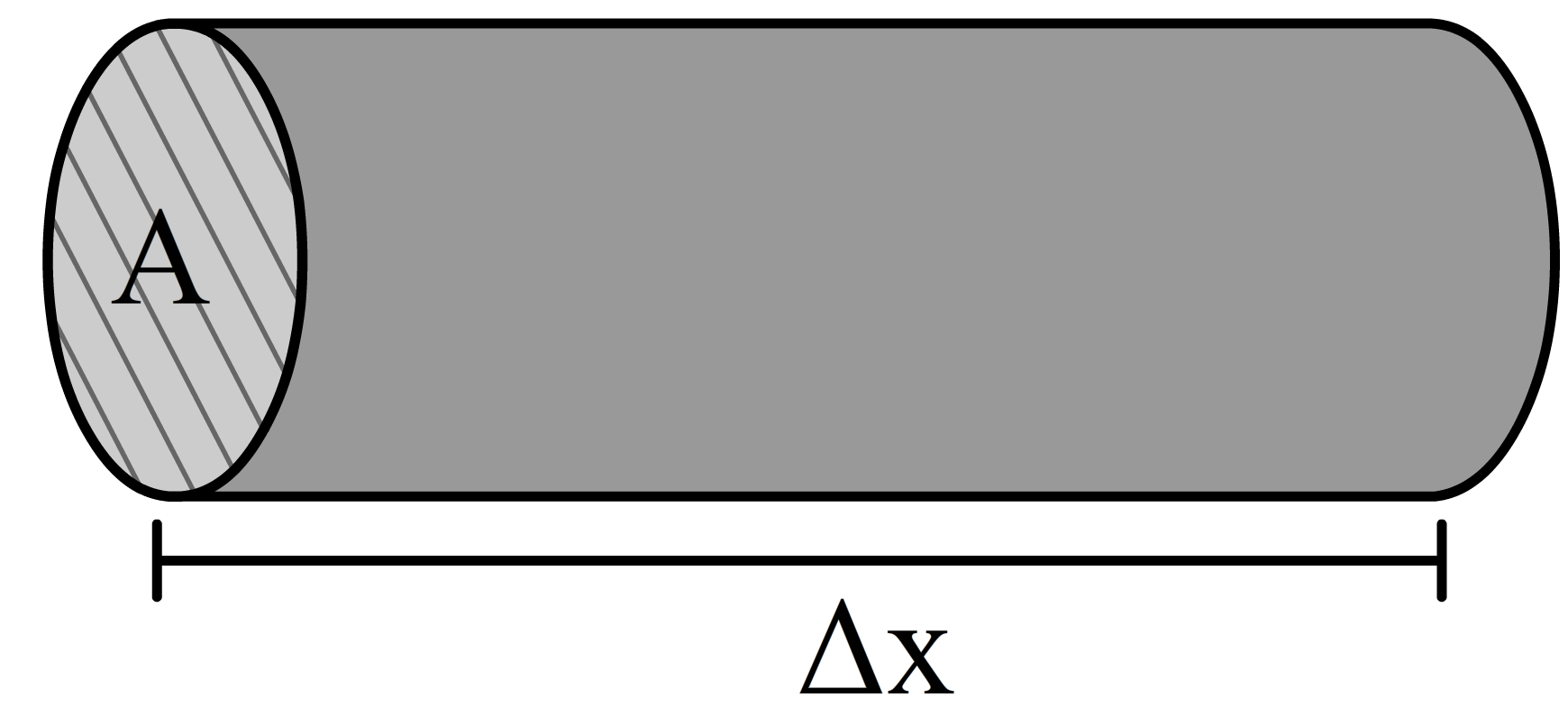
Als we dit in de formule voor het debiet stoppen, dan vinden we:
$$ Q = \frac{\Delta V}{\Delta t} = \frac{A \times \Delta x}{\Delta t} $$Omdat "v = Δx/Δt", kunnen we dit herschrijven tot:
$$ Q = v \times A $$
|
We zien hieronder een slang afgebeeld met aan de linkerkant een grotere opening dan aan de rechterkant. Als er water door de gehele slang stroomt, moet er evenveel water in als uit de slang stromen. Het water kan immers nergens anders heen. Het debiet in de slang is dus overal gelijk.
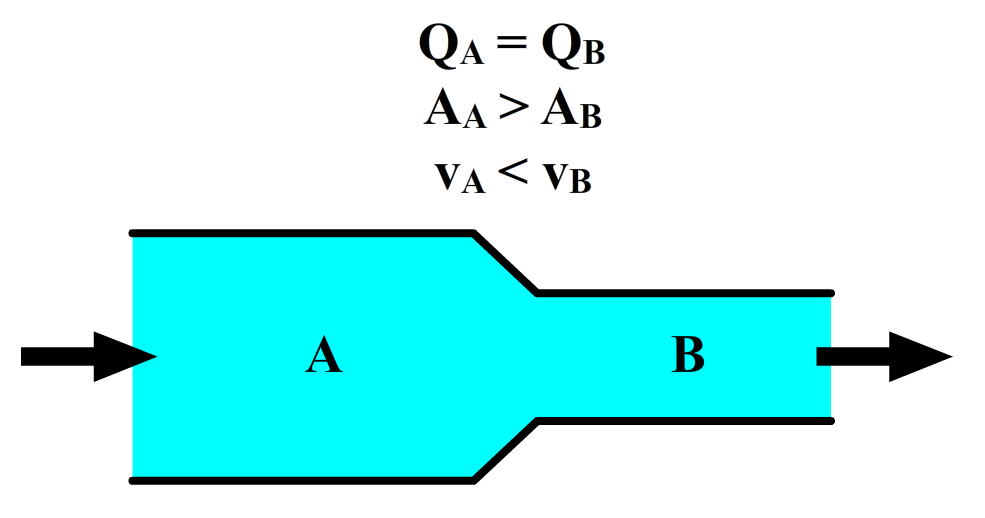
We zien aan de formule "Q = vA" dat als we het debiet gelijk houden, maar de doorsnede verkleinen, dat dan de snelheid van de vloeistof toeneemt. De snelheid van het water is aan de rechterzijde dus groter. We zien dit effect bijvoorbeeld als we onze duim deels over de opening van een tuinslang houden. Het water schiet er dan met een veel grotere snelheid uit (zie de onderstaande afbeelding en het onderstaande filmpje).

 Demonstratievideo
Demonstratievideo
| ||
|
 Demonstratievideo
Demonstratievideo
| ||
|
 Voorbeeld
Voorbeeld
|
|
Opdracht: Door een tuinslang stroomt een constante hoeveelheid water. Op één plek is om de slang een elastiek gebonden waardoor de diameter van de slang 2 keer zo klein wordt. Bereken welke factor de snelheid van water bij dit elastiek groter of kleiner is dan in de rest van de slang. Antwoord: In de tuinslang is het debiet (Q) overal gelijk. Als de diameter 2 keer zo klein is, dan is ook de straal 2 keer zo klein. Volgens de formule "A = πr2" is de doorsnede dan 2 × 2 = 4 keer zo klein. Volgens de formule "v = Q / A" is bij een gelijk debiet en bij een 4 keer zo kleine doorsnede de snelheid 4 keer zo groot. Opdracht: Tijdens een harde regenbui valt in een uur 25 mL regen. De regenbui valt op een plat dak met een oppervlak van 50 m2. Het water wordt weggevoerd via een dakgoot met een diameter van 5,0 cm. Het water stroomt net snel genoeg weg zodat de waterstand op het dak constant blijft. Bereken de snelheid waarmee het water door de dakgoot stroomt. Antwoord: In het uur is het totale volume regen dat gevallen is op het dak gelijk aan: ΔV = 50 × 0,025 = 1,25 m3. Hiermee kunnen we het debiet uitrekenen: $$ Q = \frac{\Delta V}{\Delta t} $$ $$ Q = \frac{1,25}{60 \times 60} = 3,4722 \times 10^{-4} \text{ m}^3\text{/s} $$Omdat het waterniveau op het dak constant is, moet het debiet in de goot gelijk zijn. Met een straal van 0,050 meter is de doorsnede van de goot gelijk aan: $$ A = \pi r^2 $$ $$ A = \pi(0,050/2)^2 = 1,963 \times 10^{-3} \text{m}^2 $$De snelheid waarmee het water wegstroomt wordt hiermee: $$ v = \frac{Q}{A} $$ $$ v = \frac{3,4722 \times 10^{-4}}{1,963 \times 10^{-3}} = 0,17 \text{ m/s} $$
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§7 Druk (VWO)
In deze paragraaf gaan we zien dat ook de druk te begrijpen is met behulp van het deeltjesmodel. Als toepassing bestuderen we ook de luchtdruk.
Laten we beginnen met het introduceren van het begrip druk. Als een persoon op de grond staat, dan oefenen zijn zolen een gewichtkracht uit op de grond. Deze kracht wordt verdeeld over het oppervlak van zijn twee schoenzolen. De kracht per bepaald oppervlak, bijvoorbeeld per cm2 of m2, wordt de druk genoemd. We rekenen dit als volgt uit:
| Druk (p) | Pascal (Pa) |
| Kracht (F) | newton (N) |
| Doorsnede (A) | vierkante meter (m2) |
De SI-eenheid van de druk is de pascal (Pa) en dit is gelijk aan newton per vierkante meter (N/m2).
Laten we een paar toepassingen bespreken. Als je op ijs loopt en het ijs begint te scheuren, dan is het verstandig om te gaan liggen en op je buik naar de kant te kruipen. Op deze manier verdeel je jouw gewichtkracht namelijk over een groter oppervlak en oefen je dus een kleinere druk uit op het ijs. Nog een voorbeeld. Waarom snijdt een scherp mes zoveel beter dan een bot mes? Dit komt doordat bij een scherp mes het snijoppervlak kleiner is en hierdoor wordt de druk juist groter. Als gevolg kan je met dezelfde hoeveelheid kracht veel beter snijden.
In het onderstaande filmpje zien we nog een voorbeeld. Een persoon gaat op dramatische wijze op een spijkerbed liggen. Als je op een enkele spijker zou gaan liggen zou dit veel pijn doen vanwege het kleine oppervlak van de punt van de spijker (kijk maar eens wat er met de citroen gebeurt aan het begin van het filmpje). Als een persoon echter op een bed van spijkers gaat liggen, dan verdeelt de persoon zijn gewicht over de oppervlakjes van alle spijkers tezamen. Als gevolg doet dit geen pijn.
Ook gassen oefenen druk uit. Het bekendste voorbeeld hiervan is de luchtdruk. De luchtdruk ontstaat door het botsen van de deeltjes waaruit de lucht bestaat. De luchtdruk is groter dan mensen vaak denken. Lucht heeft een kleine dichtheid (slechts 1,23 kg/m3), maar de volledige massa van de atmosfeer boven ons hoofd is behoorlijk groot. De massa van alle lucht boven een vierkante meter aardoppervlak heeft bijvoorbeeld een massa van ongeveer 10.000 kg! Als gevolg ervaren we per vierkante meter een luchtdruk van:
$$ p = \frac{F}{A} = \frac{1,0 \times 10^4 \times 9,81}{1,0} \approx 1,0 \times 10^5 \text{ Pa} $$De luchtdruk op zeeniveau is dus gelijk aan 1,0 × 105 Pa (of iets nauwkeuriger 1,013 × 105 Pa). Naast de pascal wordt ook wel de eenheid bar gebruikt. 1 bar komt overeen met 100 kPa. De luchtdruk is dus ongeveer gelijk aan 1 bar.
In het dagelijks leven merken we relatief weinig van deze hoge luchtdruk. Dit komt doordat de luchtdruk zichzelf meestal in evenwicht houdt. De luchtdruk die bijvoorbeeld op de bovenkant van je arm werkt, is even groot als de luchtdruk die op de onderkant van je arm werkt. De grootte van de luchtdruk wordt wel merkbaar in het volgende experiment. In de onderstaande afbeelding zien we twee halve bollen die losjes tegen elkaar aangelegd zijn (de zogenaamde maagdenburger halve bollen). De lucht van buiten drukt de halve bollen tegen elkaar aan, maar de lucht aan de binnenkant biedt een even grote tegendruk. Als gevolg merk je ook hier niet van de luchtdruk en kunnen we de halve bollen moeiteloos weer van elkaar afhalen.
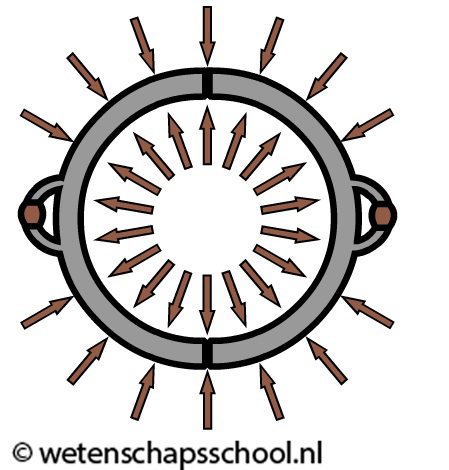
Maar als we de lucht aan de binnenkant wegpompen, dan valt de tegendruk weg. De lucht drukt nu alleen nog vanaf buiten tegen de halve bollen (zie de onderstaande afbeelding). In dit geval krijgt zelfs de sterkste man op aarde de halve bollen niet uit elkaargetrokken!
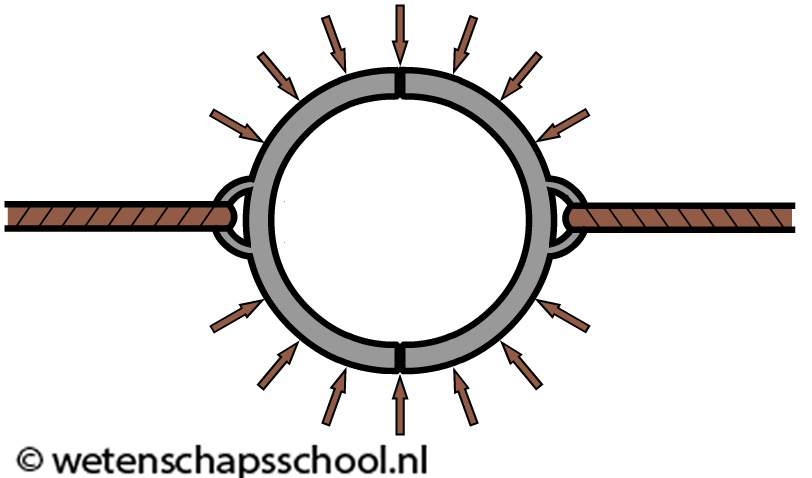
Sterker nog, in de 17de eeuw is geprobeert met zestien paarden de bollen uit elkaar te trekken, maar ook dit lukte niet!

In het onderstaande filmpje zien we de maagdenburger halve bollen in werking:
Eenzelfde soort effect zien we als we bijvoorbeeld een ballon in een vacuümruimte plaatsen (zie het volgende filmpje). Doordat de luchtdruk van buitenaf wegvalt, neemt de druk van binnen in de ballon de overhand. Hierdoor zet de ballon uit.
Een dramatische versie van de kracht van luchtdruk zien we in het onderstaande filmpje. Door een groot metalen vat met een opening aan de bovenkant te verwarmen zet de lucht aan de binnenkant uit, waardoor lucht via de opening gaat ontsnappen. Daarna wordt de opening gedicht en wordt het vat afgekoeld, zodat de druk aan de binnenkant daalt. Als gevolg krijgt de luchtdruk aan de buitenkant de overhand en knalt het vat in elkaar.
Hoe hoger je in de atmosfeer komt, hoe minder lucht er boven je bevindt en hoe lager de luchtdruk dus wordt. In het onderstaande diagram kan je zien hoe de luchtdruk verandert met de hoogte. Deze grafiek wordt op een slimme manier gebruikt in een vliegtuig. Door de luchtdruk buiten het vliegtuig te meten, kan je met deze grafiek de hoogte van het vliegtuig bepalen.
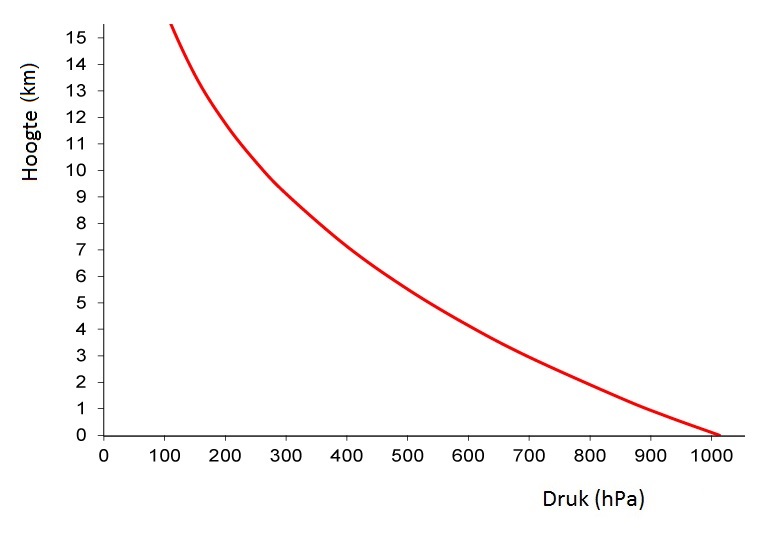
Als je een erg hoog de bergen in gaat, dan neemt de luchtdichtheid op een gegeven moment zo ver af dat het lastiger wordt om te ademen. Op grote hoogte is het daarom nodig om zuurstofflessen mee te nemen. Ook de druk is hier een stuk lager. Dit merk je bijvoorbeeld als je op grote hoogte water wilt koken. Op zeeniveau duwt de lucht hard tegen het wateroppervlak. De bellen die bij het koken ontstaan, kunnen hierdoor lastig vormen. Zoals je weet kunnen deze bellen op zeeniveau pas vormen bij een temperatuur van 100 °C (het kookpunt). Op de top van de Mount Everest gebeurt dit door de lage luchtdruk al bij 71 °C. Als gevolg doet het koken van een ei op de top van een hoge berg veel langer.
Nog extremer wordt het als we water in een vacuümruimte plaatsen. Een vacuüm is een lege ruimte zonder atomen. In deze ruimte zit dus zelfs geen lucht. Er is hier dus ook geen luchtdruk aanwezig. In dat geval kookt het water zelfs al bij kamertemperatuur! Dit is te zien in het onderstaande filmpje. In het filmpje zie je nog iets bijzonders. Doordat de snelste waterdeeltjes als eerst uit het water ontsnappen, neemt de temperatuur van het water af. Dit kan je goed zien op de thermometer.
 Voorbeeld
Voorbeeld
|
|
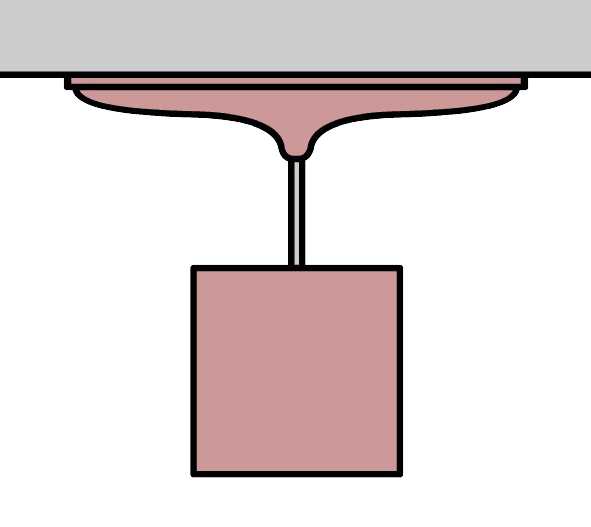
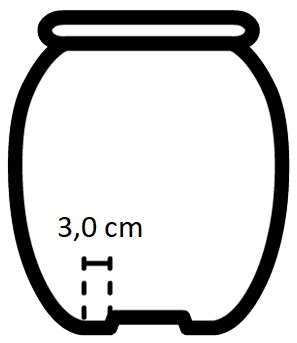
Opdracht: We bevestigen een zuignap met een diameter van 10 cm tegen een plafond (zie de onderstaande afbeelding). Bereken wat de maximale massa is die we aan de zuignap kunnen hangen zonder dat deze losschiet.
Antwoord: Voor de kracht die de lucht uitoefent op de zuignap geldt: $$ F_{lucht} = p_{lucht}A = p_{lucht} \times \pi \times r^2 $$ $$ F_{lucht} = 1,0 \times 10^5 \times \pi \times 0,050^2 = 8,0 \times 10^2 \text{ N} $$Op de zuignap werkt een zwaartekracht naar beneden en een luchtdruk omhoog. Als de kracht die de lucht uitoefent groter is dan de zwaartekracht, dan zit de zuignap stevig vast tegen het plafond. Als de kracht die de luchtdruk uitoefent even groot is aan de zwaartekracht, dan zit de zuignap nog net vast aan het plafond. Er geldt dan: $$ F_{lucht} = F_z $$Ook de zwaartekracht is dan dus gelijk aan 8,0 × 102 N. De massa van het blok is dan: $$ m = \frac{F_z}{g} = \frac{8,0 \times 10^2}{9,81} = 81 \text{ kg} $$
|
 Voorbeeld
Voorbeeld
|
|
Opdracht: Hieronder is een cilinder getekend met daarin een zogenaamde zuiger. De zuiger is een schijf die vrij naar boven en naar beneden kan bewegen in de cilinder. De zuiger heeft een massa van 2,0 kg en een onderoppervlak van 10 cm2. Bereken de luchtdruk in de cilinder.
Antwoord: De zwaartekracht oefent de volgende druk uit op de lucht in de cilinder: $$ p_z = \frac{F_z}{A} = \frac{2,0 \times 9,81}{0,001} = 2,0 \times 10^4 \text{ Pa} $$Hier tellen we de luchtdruk bij op die van boven op de zuiger drukt: $$ p_{lucht\; binnen} = p_z + p_{lucht\; buiten} $$ $$ p_{lucht\; binnen} = 2,0 \times 10^4 + 1,0 \times 10^5 = 1,2 \times 10^5 \text{ Pa} $$De luchtdruk in de cilinder is dus 1,2 × 105 Pa, iets hoger dan de luchtdruk buiten de cilinder.
|
Cilinders en zuigers worden o.a. gebruikt bij verbrandingsmotoren. In de eerst onderstaande afbeelding zien we dat er benzine in een cilinder wordt gespoten. Als de zuiger zich op zijn hoogste positie bevindt, wordt de benzine ontstoken, waardoor de temperatuur van het gas enorm toeneemt (zie de tweede afbeelding). Als gevolg ontstaat ook een grote druk waarmee de zuiger naar beneden wordt geduwd (zie de derde afbeelding). Deze beweging zorgt ervoor dat aan de onderzijde een roterende bewegen ontstaat, waarmee de wielen van bijvoorbeeld een auto kunnen worden aangedreven. In de laatste afbeelding zien we dat het warme gas dat bij de verbranding is ontstaan aan de rechterzijde wordt afgevoerd, waarna het proces weer opnieuw kan beginnen.
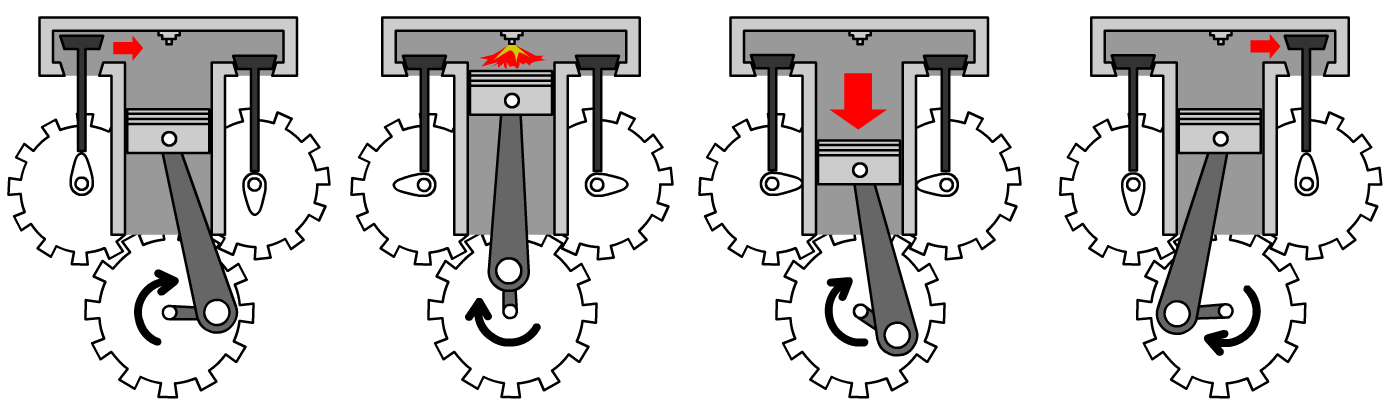
De laatste stap is van groot belang, want als het hete gas in de cilinder blijft, dan kan het ontsteken van meer benzine amper nog voor een toename van de temperatuur zorgen en als gevolg wordt de zuiger niet meer naar beneden gedrukt.
De werking van een koelkast lijkt hierop. In dit geval wordt een stof buiten de koelkast door een externe kracht onder druk gezet (hiervoor gebruiken we een elektrische pomp). Als gevolg neemt de temperatuur van de stof toe tot boven de kamertemperatuur, waarna warmte van de stof wegstroomt richting de kamer. Daarna wordt de stof de koelkast in gestroomd, waarna de druk van de stof wordt gehaald. Als gevolg zet de stof uit, waardoor de temperatuur afneemt tot onder de binnentemperatuur van de koelkast. Als gevolg stroom er nu warmte van de binnenkant van de koelkast richting de stof en neemt de temperatuur in de koelkast af.
 Redeneren met luchtdruk en vacuüm.
Redeneren met luchtdruk en vacuüm.
|
|
 Redeneren en rekenen met druk
Redeneren en rekenen met druk
|
|
§8 De ideale gaswet (VWO)
In deze paragraaf gaan we bestuderen hoe de eigenschappen van gassen veranderen als we de temperatuur, de druk, het volume en het aantal deeltjes veranderen. We noemen dit de algemene gaswet. Daarna gaan we aantonen dat deze wet volledig te verklaren is met behulp van het deeltjesmodel.
Aan de hand van een aantal experimenten gaan we de relatie tussen de druk, de temperatuur en het volume van een gas bestuderen. Voor het gemak bestuderen we een ideaal gas. Dit is een gas waarbij de interactie tussen de deeltjes verwaarloosd wordt (voor veel gassen in het dagelijks leven blijkt dit een goede benadering).
We beginnen met het volgende experiment. Een gas in een ruimte met een constant volume wordt verwarmd (zie de onderstaande afbeelding). We spreken in dit geval van een isochoor proces (isochoor wil zeggen dat het volume gelijk blijft). Door het verwarmen van het gas gaan de deeltjes sneller bewegen en doordat de deeltjes met een grotere snelheid tegen de wanden botsen is dan ook de druk hoger.
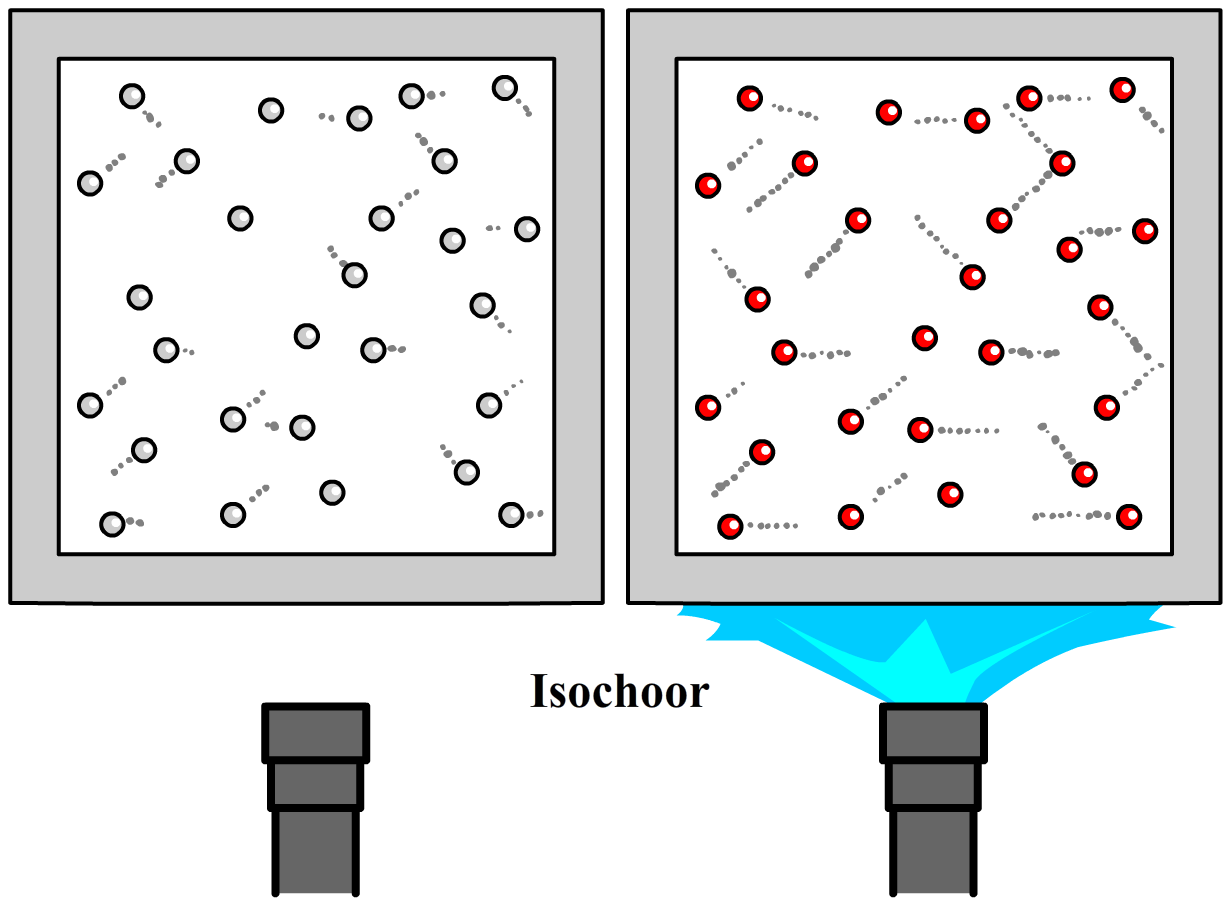
Uit experimenten blijkt dat als we de temperatuur van een gas (in kelvin) verdubbelen, dat de druk dan ook verdubbelt. Er geldt dus de volgende relatie:
$$ \frac{p}{T} = \text{constant} \;\;\;\text{(isochoor)}$$Of ook wel:
$$ \frac{p_b}{T_b} = \frac{p_e}{T_e} \;\;\;\text{(isochoor)} $$In het volgende experiment houden we de druk constant. We noemen dit een isobaar proces. We doen dit door een gas te verwarmen in een cilinder met een vrij beweegbare zuiger. Door het verwarmen gaan de deeltjes sneller bewegen en als gevolg neemt in eerste instantie de druk toe. Deze hogere druk zorgt ervoor dat de zuiger omhoog gedrukt wordt, waardoor de druk weer afneemt tot het zijn originele waarde bereikt.
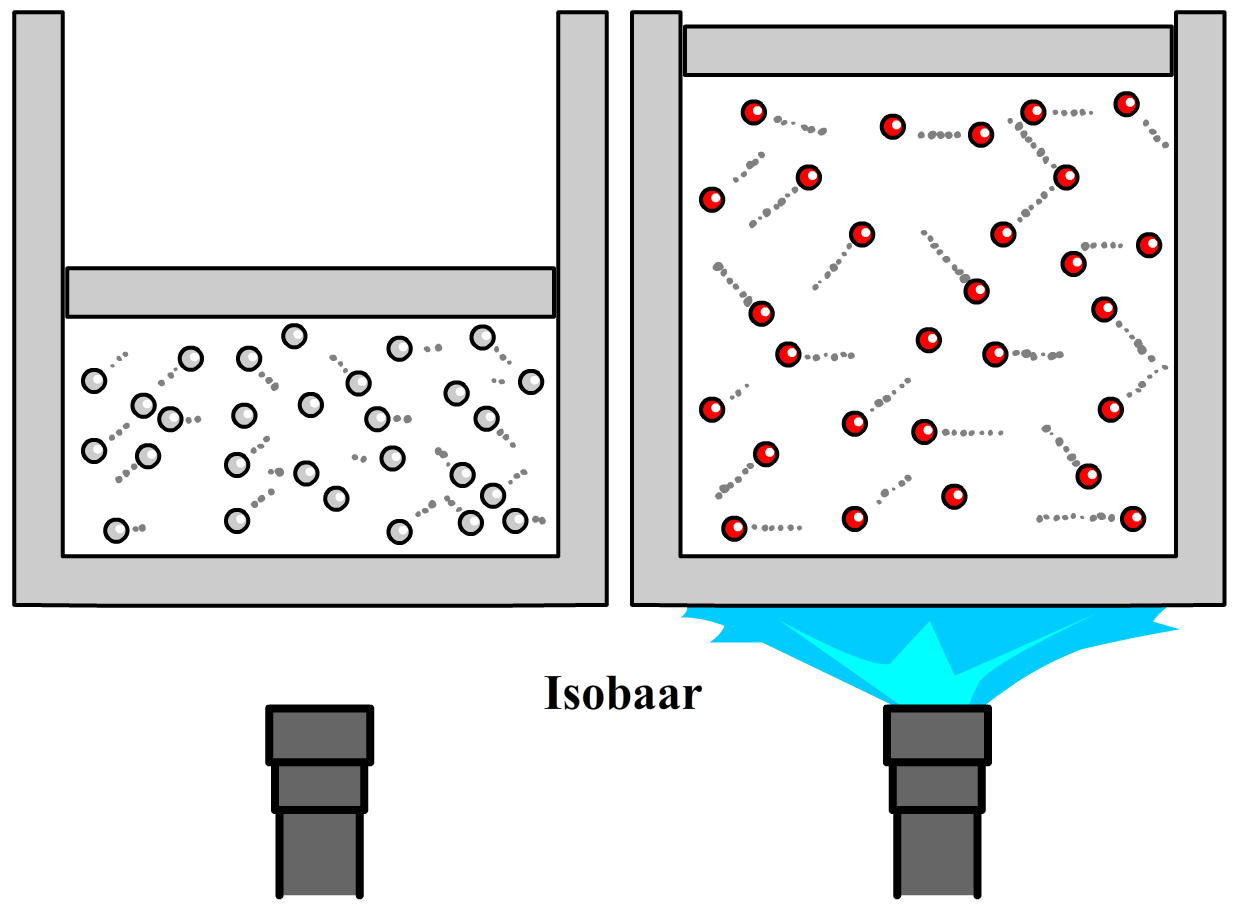
Uit experimenten blijkt dat als we de temperatuur van het gas (in kelvin) verdubbelen, dat dan ook het volume verdubbelt. Er geldt dus de volgende relatie:
$$ \frac{V}{T} = \text{constant} \;\;\;\text{(isobaar)}$$Of ook wel:
$$ \frac{V_b}{T_b} = \frac{V_e}{T_e} \;\;\;\text{(isobaar)} $$Als laatste hebben we ook nog een isotherm proces. Dit is een proces waarbij de temperatuur constant blijft. In het onderstaande experiment wordt een zuiger ingedrukt met een externe kracht. Als gevolg neemt de druk toe (want je hebt meer botsingen in de kleinere ruimte) en in eerste instantie ook de temperatuur (door de zuiger in te drukken geef je de deeltjes extra kinetische energie). Als we dan een tijdje wachten, dan wordt de temperatuur binnen de cilinder weer gelijk aan de omgevingstemperatuur.
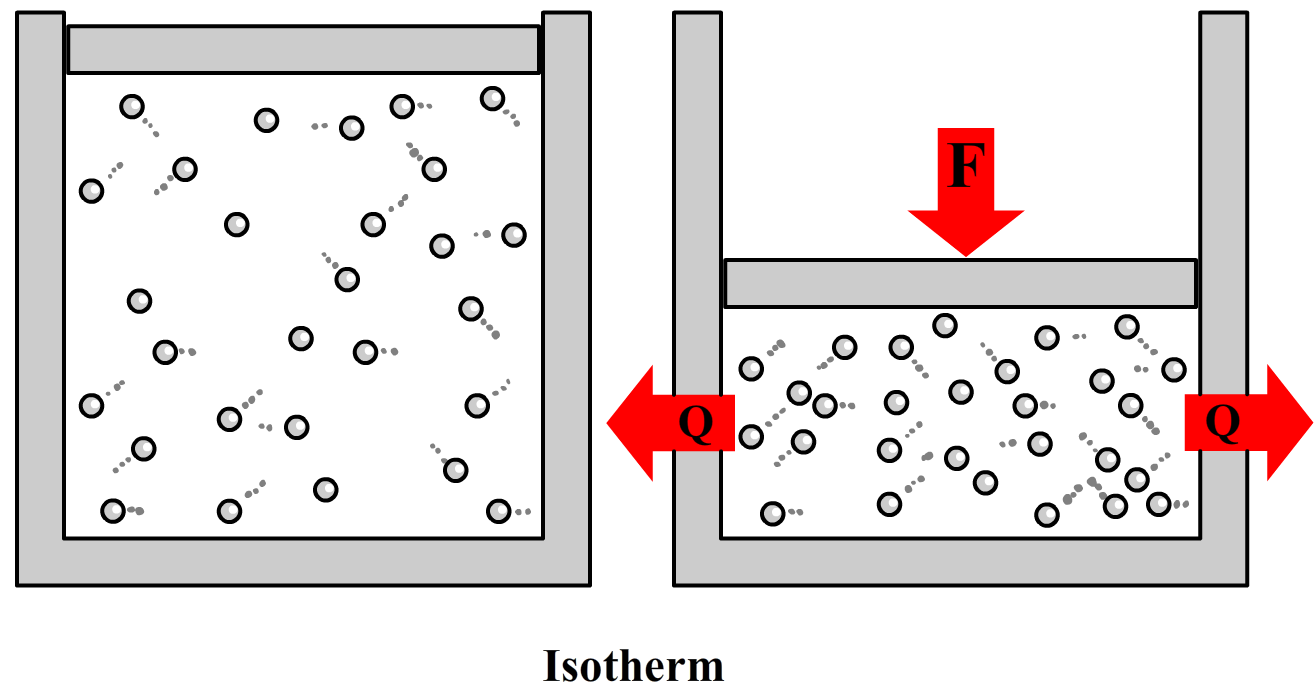
Uit experimenten blijkt dat als we het volume van het gas halveren, dat de druk dan verdubbelt. Er geldt dus de volgende relatie:
$$ pV = \text{constant} \;\;\;\text{(isotherm)}$$Of ook wel:
$$ p_bV_b = p_eV_e \;\;\;\text{(isotherm)} $$Al deze formules kunnen we combineren tot één formule genaamd de ideale gaswet:
$$ pV=Nk_BT $$
|
Met deze formnule kunnen we de voorgaande formules genereren. Bij een isobaar proces is blijvoorbeeld de druk (en het aantal deeltjes) constant. We kunnen de ideale gaswet dan omschrijven, zodat alle constanten aan de rechter kant komen te staan:
$$ \frac{V}{T} = \frac{Nk_B}{P} $$Er geldt nu dus:
$$ \frac{V}{T} = \text{constant} $$En dit is precies de vergelijking die we eerder ook hadden gevonden.
 EXTRA: Afleiding ideale gaswet
EXTRA: Afleiding ideale gaswet
|
|
In het laatste stuk van deze paragraaf gaan we de algemene gaswet afleiden aan de hand van het deeltjesmodel. We doen dit met behulp van de tweede wet van Newton. Er geldt: $$ F_{res} = ma = m\frac{\Delta v}{\Delta t} $$Stel dat een gasdeeltje horizontaal heen en weer botst in een doos van lengte L. Stel dat een deeltje vanaf de rechter wand naar links beweegt (negatieve snelheid), botst tegen de linker wand en dan weer naar rechts beweegt (positieve snelheid) naar de startpositie. Daarna begint de hele beweging weer opnieuw. De gemiddelde kracht die èèn deeltje per botsing op de linkerwand uitoefent is in dat geval: $$ F_{res} = m\frac{v_e - v_b}{\Delta t} = m\frac{v_x - (-v_x)}{\Delta t} = m\frac{2v_x}{\Delta t} $$Het deeltje heeft per botsing een afstand 2L afgelegd (heen en terug). Met de formule Δt = Δx/vx = 2L/vx kunnen we de bovenstaande formule herschrijven tot: $$ F_{res} = m\frac{v_x^2}{L} $$Tot dusver hebben we naar het botsen van één deeltje gekeken, maar in werkelijkheid bestaat het gas natuurlijk uit N deeltjes. De totale resulterende kracht op de linker wand wordt dan: $$ F_{res} = \frac{mv_{x,1}^2}{L} + \frac{mv_{x,2}^2}{L} + ... + \frac{mv_{x,N}^2}{L} $$ $$ F_{res} = \frac{m}{L}(v_{x,1}^2+v_{x,2}^2+ ... +v_{x,N}^2)$$Als we beide zijden delen door N, dan vinden we dan vinden we aan de rechterzijde het gemiddelde van het kwadraat van de snelheden van de deeltjes: $$ \frac{F_{res}}{N} = \frac{m}{L}\frac{(v_{x,1}^2+v_{x,2}^2+ ... +v_{x,N}^2)}{N} = \frac{m}{L}(v_x^2)_{gem} $$Dit kunnen we herschrijven tot: $$ F_{res} = \frac{Nm}{L}(v_x^2)_{gem} $$Met de formule p = F/A kunnen we hiermee de druk van het gas uitrekenen: $$ p = \frac{F}{A} = \frac{Nm}{AL}(v_x^2)_{gem} = \frac{Nm}{V}(v_x^2)_{gem} $$In de laatste stap hebben we gebruikt dat het oppervlak van de linker wand maal de lengte van de doos gelijk is aan het volume. Aan deze formule moeten nog een aanpassing doen. Tot nu toe zijn we ervan uitgegaan dat alle deeltjes horizontaal bewegen (parallel aan de x-as). In werkelijkheid zullen de deeltjes ook in de y-richting of de z-richting bewegen. De druk tegen de linkerwant zal dus een factor drie lager zijn dan we hierboven hebben berekend. We vinden dus: $$ PV = \frac{1}{3}Nm(v_x^2)_{gem} $$Deze formule begint al een beetje de vorm aan te nemen van de ideale gaswet. We moeten echter nog een toevoeging doen. In de 19de eeuw werd experimenteel vastgesteld met welke snelheid deeltjes in een gas bewegen. Er werd gevonden dat: $$ (v^2)_{gem} = \frac{3k_BT}{m} $$We kunnen dit herschrijven tot: $$ k_BT = \frac{1}{3} m (v^2)_{gem} $$Met deze formule kunnen we de ideale gaswet direct herschrijven tot: $$ PV = Nk_BT $$Dit is precies de wet die we ook in de paragraaf zijn tegengekomen! We hebben hiermee de ideale gaswet dus afgeleid met het deeltjesmodel. |
 Redeneren met luchtdruk en vacuüm.
Redeneren met luchtdruk en vacuüm.
|
|
| BINAS: | |
| 7 | De constante van Wien |
| 8-12 | Dichtheid en soortelijke warmte |
| 8-12 | Warmtegeleidingscoëfficiënt |
| 19A | Het zichtbare spectrum |
| 19B | Het volledige spectrum |
| 23 | Planck-kromme |
| 28B | Stookwaarde |