Hoofdstuk 2
Beweging
§1 De gemiddelde snelheid §2 Versnelling §3 Het (x,t)-diagram §4 Het (v,t)-diagram §5 De oppervlaktemethode
§1 De gemiddelde snelheid
In dit hoofdstuk gaan we bewegingen bestuderen. Je kan hier denken aan het bewegen van een raket in een baan om de maan of gewoon het fietsen van huis naar school. In deze eerste paragraaf gaan we leren rekenen met de gemiddelde snelheid.
Als een voorwerp met een constante snelheid beweegt, dan kunnen we deze snelheid uitrekenen met de volgende formule:
$$ v = \frac{\Delta x}{\Delta t} $$
|
De "x" staat voor de positie van een voorwerp. Het "Δ"-teken staat voor "de toename van". "Δx " staat dus voor de toename van de positie tijdens de beweging. We noemen dit ook wel de verplaatsing. "Δt" staat voor de toename van de tijd tijdens de beweging. We noemen dit ook wel de tijdsduur.
De SI-eenheid van de snelheid is meter per seconde, maar in het dagelijks leven wordt ook vaak kilometer per uur gebruikt. Het is belangrijk dat je deze eenheden in elkaar om kan schrijven. Stel we willen 80 km/h omrekenen naar m/s. We rekenen dan eerst kilometer per uur om naar meter per uur:
$$ 80 \text{ km/h} = 80 000 \text{ m/h} $$Dan rekenen we meter per uur om naar meter per seconde:
$$ \frac{80 000 \text{ m/h}}{60 \times 60} = 22 \text{ m/s} $$Stel we willen 22 m/s omrekenen naar km/h. We rekenen dan eerst meter per seconde om naar meter per uur:
$$ 22 \text{ m/s} \times 60 \times 60 = 80 000 \text{ m/h} $$Daarna rekenen we om naar kilometer per uur:
$$ 80 000 \text{ m/h} = 80 \text{ km/h} $$We kunnen bij het omschrijven ook gebruik maken van de volgende regel:
|
|
 Stappenplan: Rekenen met snelheid
Stappenplan: Rekenen met snelheid
|
|
Vraag: Een leerling is aan het hardlopen. Zijn doel is om binnen drie minuten 1,0 kilometer te rennen. De leerling rent 3,0 minuten lang met een snelheid van 18 km/h. Bereken of de leerling zijn doel bereikt heeft. Stap 1: Gegevens (G) Schrijf de gegevens uit de vraag op: Δt = 3,0 min v = 18 km/h Δx = ... m Stap 2: Omschrijven (O) Reken de gegevens zoveel mogelijk om in dezelfde eenheden. In dit geval rekenen we alles om naar meters en seconden. Omdat er 60 seconden in een minuut zitten, vinden we: Δt = 3,0 × 60 = 180 s v = 18 / 3,6 = 5,0 m/s Stap 3: Formule (F) Noteer de formule in de juiste vorm. In dit geval willen we de verplaatsing (Δx) weten: $$ \frac{\Delta x}{\Delta t} = v \;\;\;\;\; \rightarrow \;\;\;\;\; \Delta x = v \times \Delta t $$Stap 4: Invullen en Rekenen (IR) Vul de formule in: $$ \Delta x = 5,0 \times 180 = 9,0 \times 10^2 \text{ m} = 0,90 \text{ km} $$Stap 5: Eenheid (E) Denk aan de eenheid achter het antwoord. In dit geval is de eenheid m. Stap 6: Conclusie (C) Schrijf de conclusie op en leg uit hoe je aan deze conclusie komt. 0,90 km is minder dan 1,0 kilometer, dus de leerling heeft zijn doel niet bereikt.
|
Als de snelheid van een voorwerp niet constant is, dan kunnen we wel de gemiddelde snelheid uitrekenen. Dit doen we als volgt:
$$ v_{gem} = \frac{\Delta x}{\Delta t}$$
|
Als een voorwerp geleidelijk versnelt of vertraagt, dan spreken we van een eenparige versnelling. In dit geval kunnen we de gemiddelde snelheid ook als volgt uitrekenen:
$$ v_{gem} = \frac{v_{b}+v_{e}}{2} \;\;\;\; \text{(eenparige versnelling)} $$
|
Stel dat een auto bijvoorbeeld eenparig versnelt van 10 m/s naar 30 m/s, dan is de gemiddelde snelheid gelijk aan:
$$ v_{gem} = \frac{v_b+v_e}{2} = \frac{10+30}{2} = 20 \text{ m/s} $$Let erop dat je als volgt haakjes gebruikt in je rekenmachine:
$$ (10 + 30 )/2 = 20 \;\;\;\;\;\;\; \text{ rekenmachine} $$
 Voorbeeld
Voorbeeld
|
|
Opdracht: Een auto versnelt gedurende 10 seconden van 20 naar 30 m/s. De versnelling is eenparig. Bereken hoeveel meter de auto heeft afgelegd. Antwoord: Eerst berekenen we de gemiddelde snelheid:… $$v_{gem} = \frac{v_{\text{begin}}+v_{\text{eind}}}{2} $$ $$v_{gem} = \frac{20 + 30}{2} = 25 \text{ m/s}$$Met de gemiddelde snelheid kunnen we de afstand uitrekenen. In dit geval willen we de verplaatsing (Δx) weten: $$ v_{gem} = \frac{\Delta x}{\Delta t} \;\;\rightarrow \;\; \Delta x = v_{gem} \times \Delta t $$Nu vullen we de formule in: $$\Delta x = v_{gem} \times \Delta t $$ $$\Delta x = 25 \times 10 = 2,5 \times 10^2 \text{ m}$$De auto heeft tijdens de versnelling dus 2,5 × 102 m afgelegd.
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§2 Versnelling
In deze paragraaf gaan we leren rekenen met de versnelling.
De versnelling of vertraging (a) van een voorwerp kunnen we als volgt uitrekenen:
$$ a = \frac{\Delta v}{\Delta t} $$
|
Zoals je weet staat de "v" voor de snelheid. "Δv" staat dan dus voor de toename van de snelheid tijdens een beweging. Als een voorwerp bijvoorbeeld versnelt van 10 m/s naar 14 m/s, dan is de toename van de snelheid gelijk aan
"Δv = 14 – 10 = 4 m/s". In formuletaal kunnen we "Δv" als volgt uitrekenen:
| $$ \Delta v = v_{eind} - v_{begin} $$ |
De eenheid van de versnelling is m/s2. Dit betekent het volgende. Stel dat de snelheid van een voorwerp elke seconde 1 meter per seconde toeneemt. We zeggen dan dat de snelheid 1 meter per seconde per seconde toeneemt. De eenheid van de versnelling is dus m/s/s en dit korten we ook wel af tot m/s2.
 Voorbeeld
Voorbeeld
|
|
Opdracht: Een persoon versnelt eenparig van 1,0 m/s naar 4,0 m/s in 6,0 seconden. Bereken de versnelling van deze persoon. Antwoord: Eerst schrijven we de gegevens op: vb = 1,0 m/s ve = 4,0 m/s t = 6,0 s Hiermee berekenen we eerst de toename van de snelheid (Δv): $$ \Delta v = v_{eind} - v_{begin} $$ $$ \Delta v = 4,0 - 1,0 = 3,0 \text{ m/s} $$Nu berekenen we de versnelling: $$ a = \frac{\Delta v}{t} $$ $$ a = \frac{3,0}{6,0} = 0,50 \text{ m/s}^2 $$ |
Let op het verschil tussen de toename van de snelheid (Δv) en de gemiddelde snelheid (vgem). Bij het beantwoorden van vragen is het belangrijk deze begrippen goed uit elkaar te houden. In het vorige voorbeeld is de toename van de snelheid gelijk aan 4,0 - 1,0 = 3,0 m/s. De gemiddelde snelheid is hier (1,0 + 4,0)/2 = 2,5 m/s.
Ook vertraging kunnen we met deze formule beschrijven. Stel dat een auto gedurende 4,0 seconden vertraagt van 40 m/s naar 12 m/s. De vertraging wordt dan:
$$ \Delta v = v_{eind} - v_{begin} $$ $$\Delta v = 12 - 40 = -28 \text{ m/s}$$ $$ a = \frac{\Delta v}{\Delta t} $$ $$ a = \frac{-28}{4,0} = -7,0 \text{ m/s}^2$$
Een versnelling van -7,0 m/s2 is dus gelijk aan een vertraging van 7,0 m/s2. Let erop dat een vertraging niet hoeft te betekenen dat het voorwerp achteruit beweegt! Een remmende auto vertraagt bijvoorbeeld, maar gaat wel vooruit.
 Stappenplan: Rekenen met versnelling
Stappenplan: Rekenen met versnelling
|
|
Opdracht: Een auto versnelt eenparig van 36 km/h naar 90 km/h en legt tijdens deze versnelling 105 meter af. Bereken de versnelling van de auto. Stap 1: Schrijf de gegevens uit de vraag op en reken ze zoveel mogelijk om in dezelfde eenheden: Δx = 105 m Stap 2: Bereken zo mogelijk "vgem" en "Δv": $$ v_{gem} = \frac{v_b + v_e}{2} = \frac{10 +25}{2} = 17,5 \text{ m/s}$$ $$ \Delta v = v_e-v_b = 25 - 10 = 15 \text{ m/s} $$Stap 3: Schrijf de formules op en geef aan welke gegevens je weet en welk gegeven je wilt weten:
Stap 4: Bedenk welke formule je wilt gebruiken. In dit voorbeeld willen we de versnelling berekenen met de rechter formule, maar we hebben nog niet alle gegevens om dit te kunnen doen. We beginnen daarom met de linker formule. Stap 5: Schrijf de formule zo nodig om en vul hem in: $$ \Delta t = \frac{\Delta x}{v_{gem}} $$ $$ \Delta t = \frac{105}{17,5} = 6,0 \text{ s} $$Stap 6: Gebruik nu de andere formule: $$ a = \frac{\Delta v}{\Delta t} $$ $$ a= \frac{15}{6,0} = 2,5 \text{ m/s}^2 $$Stap 7: Schrijf de conclusie op en denk aan de eenheid: De versnelling van de auto is 2,5 m/s2. |
 Demonstratievideo
Demonstratievideo
| ||
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
Level 1:
Level 2:
|
§3 Het (x,t)-diagram
Behalve met formules, kunnen we beweging ook beschrijven met grafieken. In deze paragraaf gaan we kijken naar de zogenaamde (x,t)-diagrammen. Ook gaan we leren de snelheid te bepalen in deze diagrammen met behulp van een raaklijn.
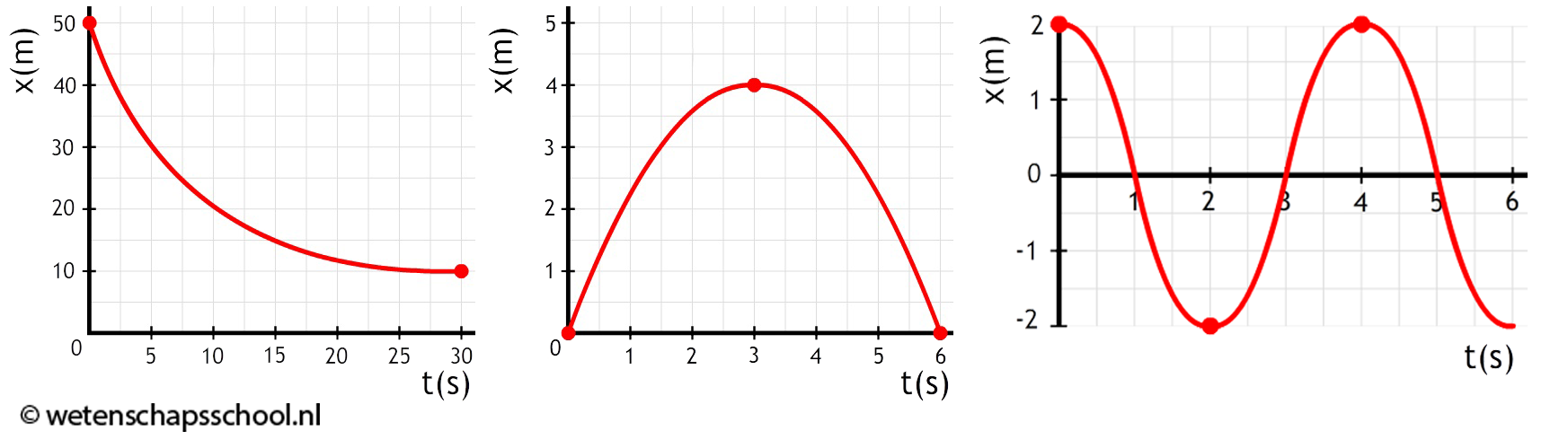
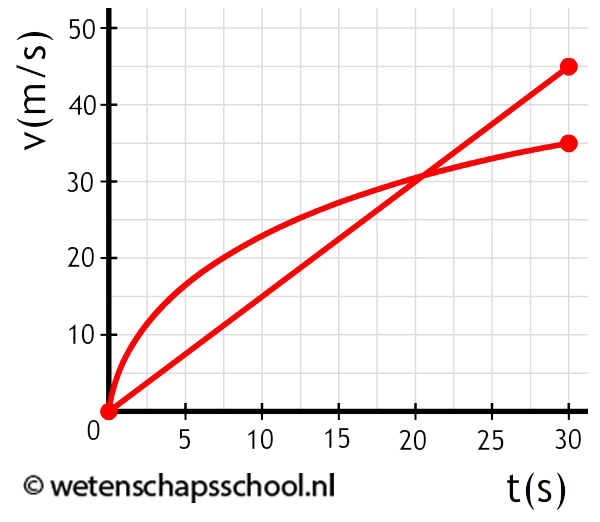
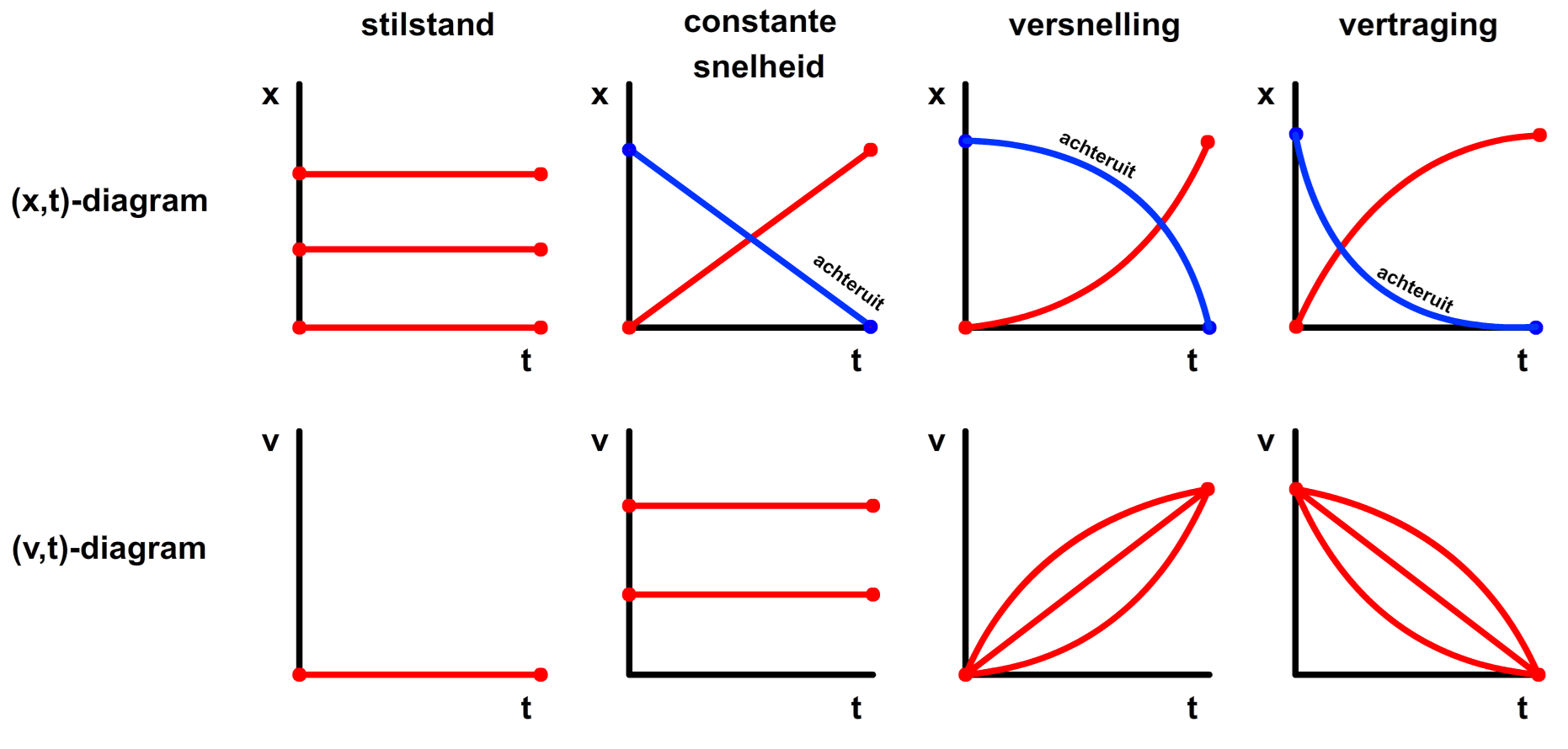
Een (x,t)-diagram is een diagram met op de horizontale as de tijd (t) en op de verticale as de positie (x). Hieronder zijn een aantal bewegingen beschreven met behulp van dit type diagram. Links zien we een grafiek die horizontaal loopt. De positie (x) verandert hier niet in de tijd. Het voorwerp staat hier dus stil. In de tweede afbeelding zien we een voorwerp dat zich geleidelijk verplaatst. Elke seconde wordt er evenveel meter afgelegd. We spreken hier van een constante snelheid of van een eenparige beweging.
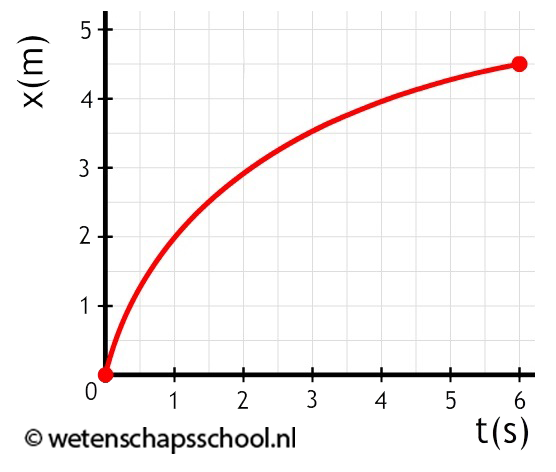
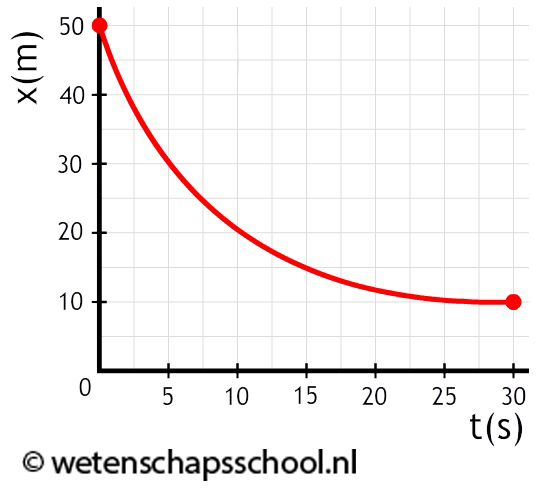
In de onderstaande linker afbeelding zien we een grafiek die steeds steiler gaat lopen. We zien dat in de eerste drie seconden slechts 0,5 meter wordt afgelegd en dat in de laatste drie seconden wel 4,5 m wordt afgelegd. Er geldt dus:
- Hoe steiler de lijn loopt, hoe sneller het voorwerp verplaatst.
We hebben hier dus te maken met een versnelling. Rechts zien we een grafiek die steeds minder steil gaat lopen. Hier hebben we dus te maken met een vertraging.
 Voorbeeld
Voorbeeld
|
|
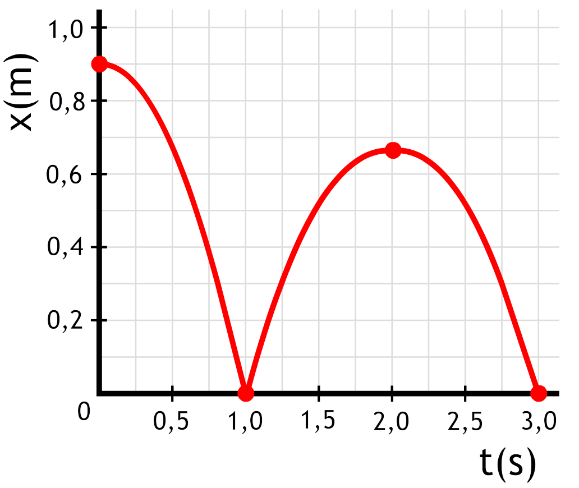
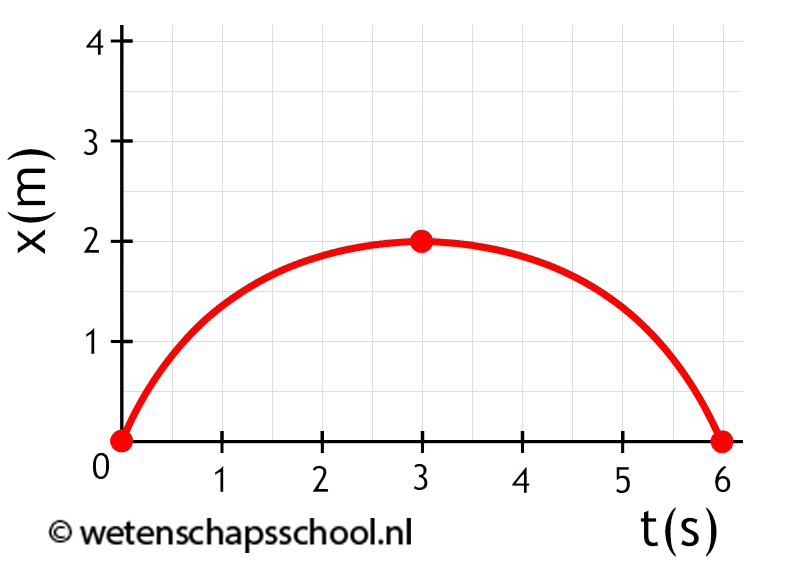
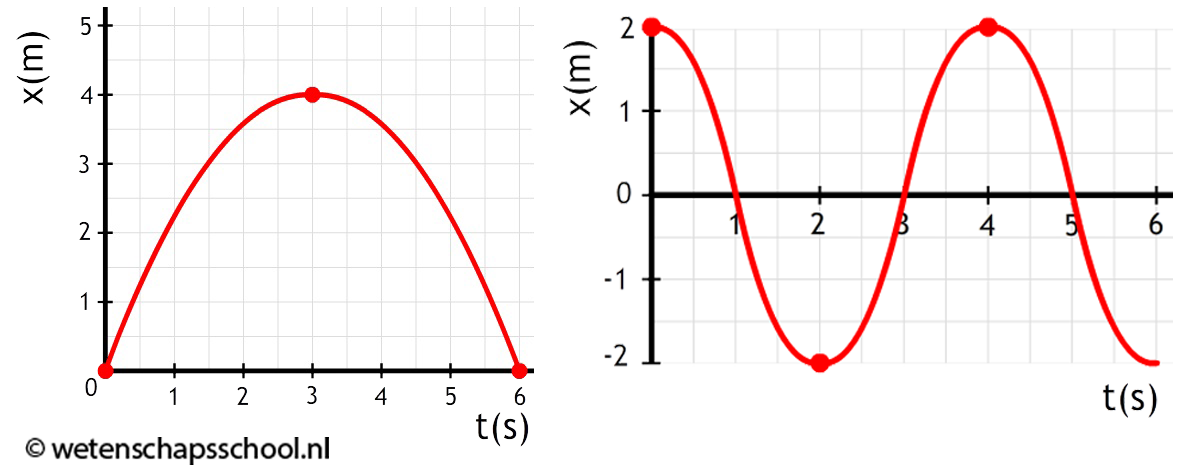
Opdracht: In het onderstaande (x,t)-diagram is de beweging van een stuiterbal weergegeven. Beschrijf deze beweging in detail.
Antwoord: In de eerste seconde loopt de grafiek steeds steiler. We hebben hier dus te maken met een versnelling. De stuiterbal gaat hier naar beneden. Op tijdstip t = 1,0 s komt de bal tegen de grond aan en gaat daarna omhoog. In de tweede seconde loopt de grafiek steeds minder steil. Hier hebben we dus te maken met een vertraging. De stuiterbal gaat hier omhoog. Op tijdstip t = 2,0 s loopt de grafiek even horizontaal. Hier staat de stuiterbal dus een moment stil op het hoogste punt van de beweging. In de derde seconde hebben we net als in de eerste seconde te maken met een versnelling naar beneden.
|
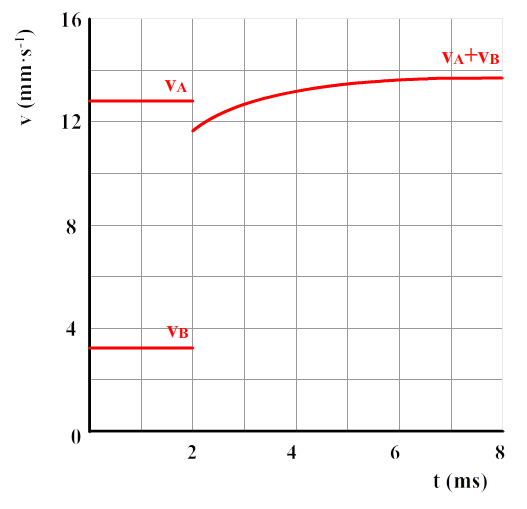
Met behulp van een (x,t)-diagram kunnen we ook de gemiddelde snelheid uitrekenen. In het onderstaande diagram is de verplaatsing (Δx) gelijk aan 4,0 meter. De tijdsduur (Δt) van de beweging is 6,0 seconden. De snelheid wordt hiermee:
$$ v_{gem} = \frac{\Delta x}{\Delta t} $$ $$ v_{gem} = \frac{4,0}{6,0} = 0,67 \text{ m/s}$$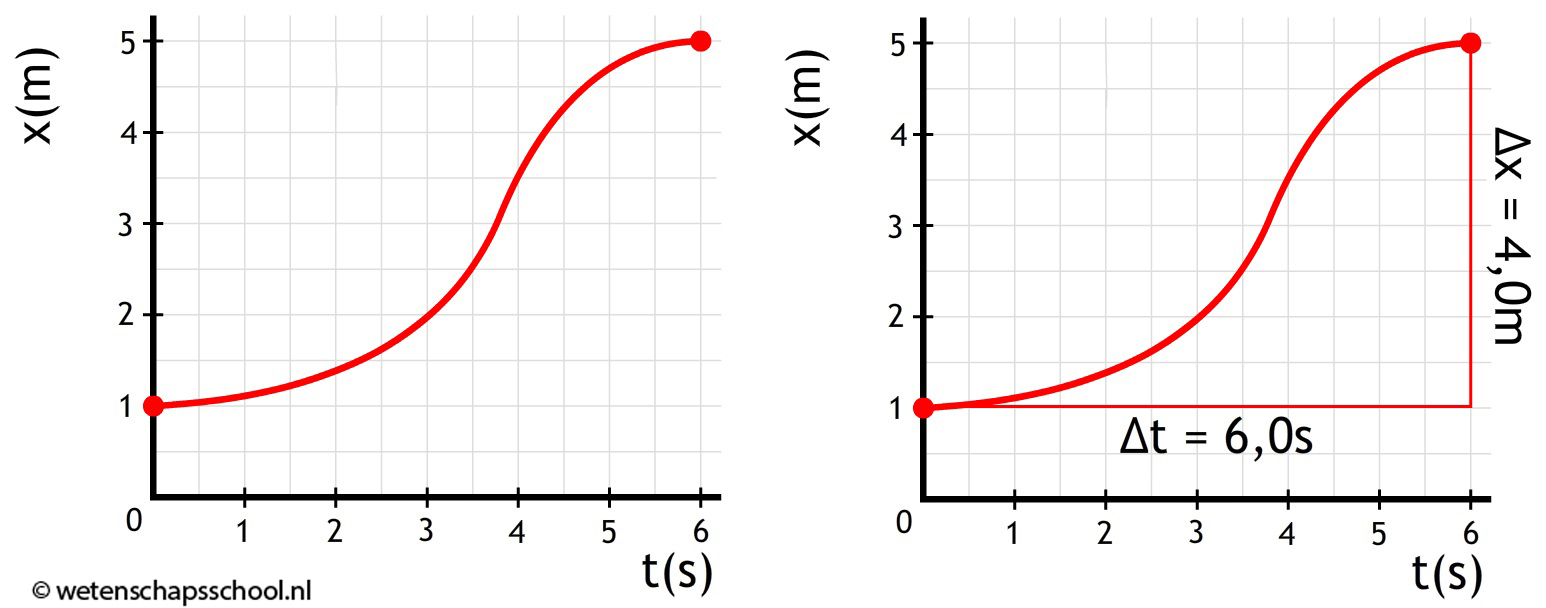
In het onderstaande (x,t)-diagram is de snelheid niet constant. Als we de snelheid op bijvoorbeeld tijdstip A willen bepalen, dan kunnen we dit doen door een klein driehoekje te tekenen en hiermee de snelheid te berekenen (zie de linker afbeelding). Dit is echter lastig meten en levert daardoor een zeer onnauwkeurig antwoord op. We kunnen dit probleem oplossen door het kleine lijnstukje in beide richtingen zoveel mogelijk te verlengen (zie de rechter afbeelding). De verlengde lijn noemen we een raaklijn. Omdat de raaklijn net zo steil loopt als het oorspronkelijke lijntje vinden we hier dezelfde snelheid.
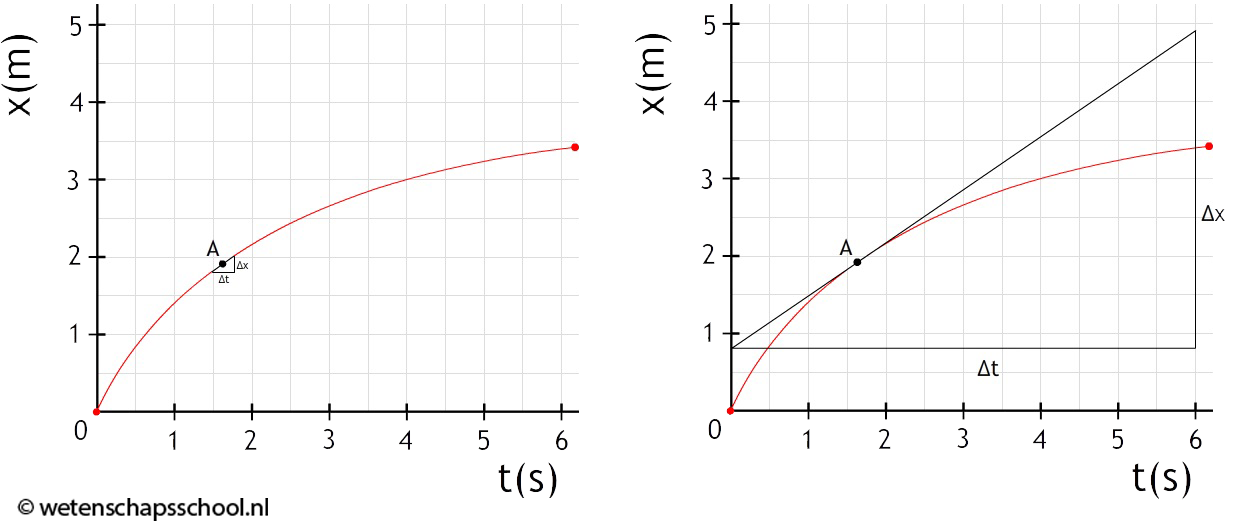
We bepalen hiermee de snelheid op één tijdstip. De bijbehorende tijdsduur (Δt) is oneindig klein en hetzelfde geldt voor de bijbehorende verplaatsing (Δx). In dat geval noteren we "Δx" als "dx" en "Δt" als "dt". De formule voor de snelheid op één tijdstip is dus:
$$ v = \frac{dx}{dt} $$De snelheid op tijdstip "A" in het bovenstaande diagram wordt hiermee:
$$ v = \frac{4,0}{6,0} = 0,67 \text{ m/s} $$
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§4 Het (v,t)-diagram
In deze paragraaf bespreken we de zogenaamde (v,t)-diagrammen. Ook hiermee kunnen we beweging beschrijven. Ook gaan we leren de gemiddelde snelheid te bepalen met behulp van dit type diagram.
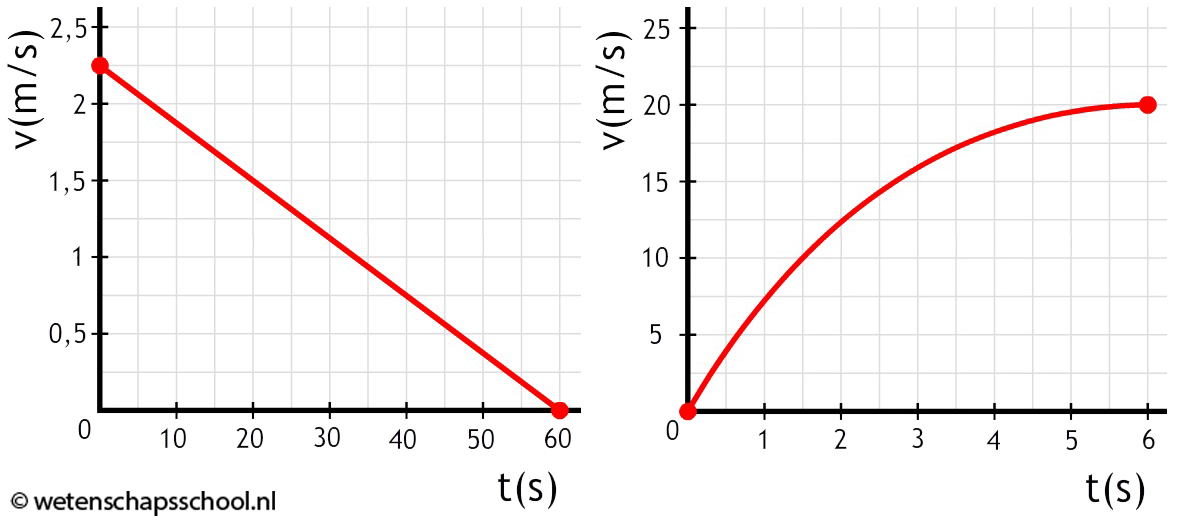
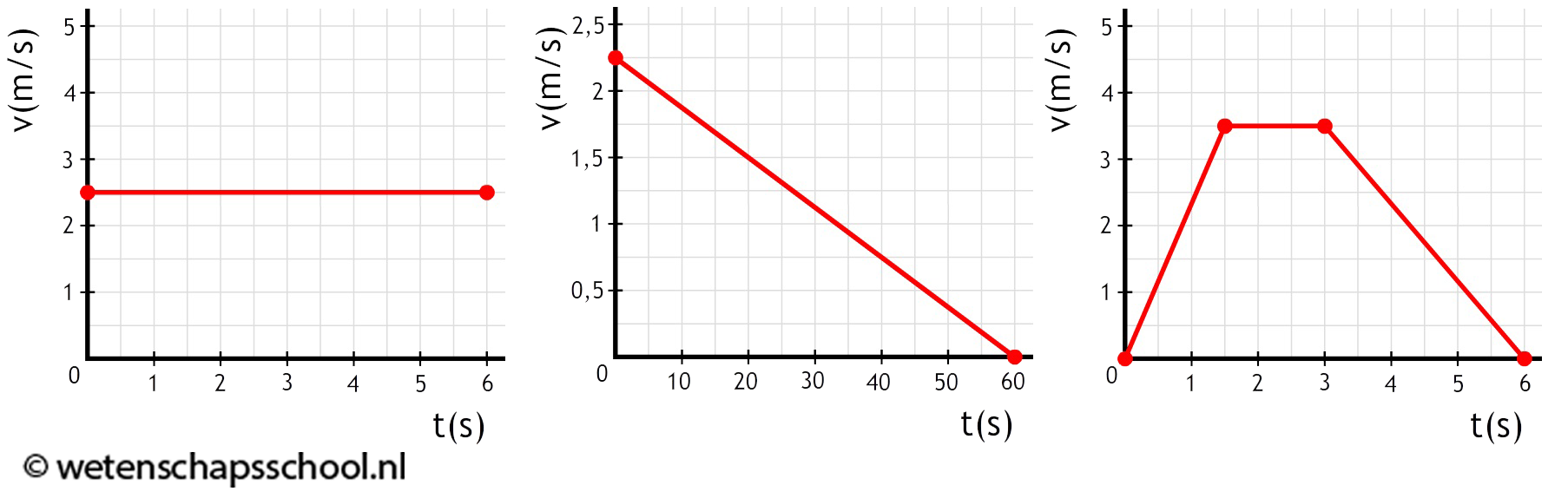
Een (v,t)-diagram is een diagram met op de horizontale as de tijd (t) en op de verticale as de snelheid (v). Hieronder zijn een aantal voorbeelden afgebeeld. Links zien we een grafiek waarbij de snelheid van een voorwerp de gehele beweging gelijk is aan 0 m/s. Het voorwerp staat in dit geval dus stil. In de tweede afbeelding zien we een voorwerp waarbij de snelheid de gehele tijd 2,0 m/s blijft. Hier hebben we dus te maken met een constante snelheid.
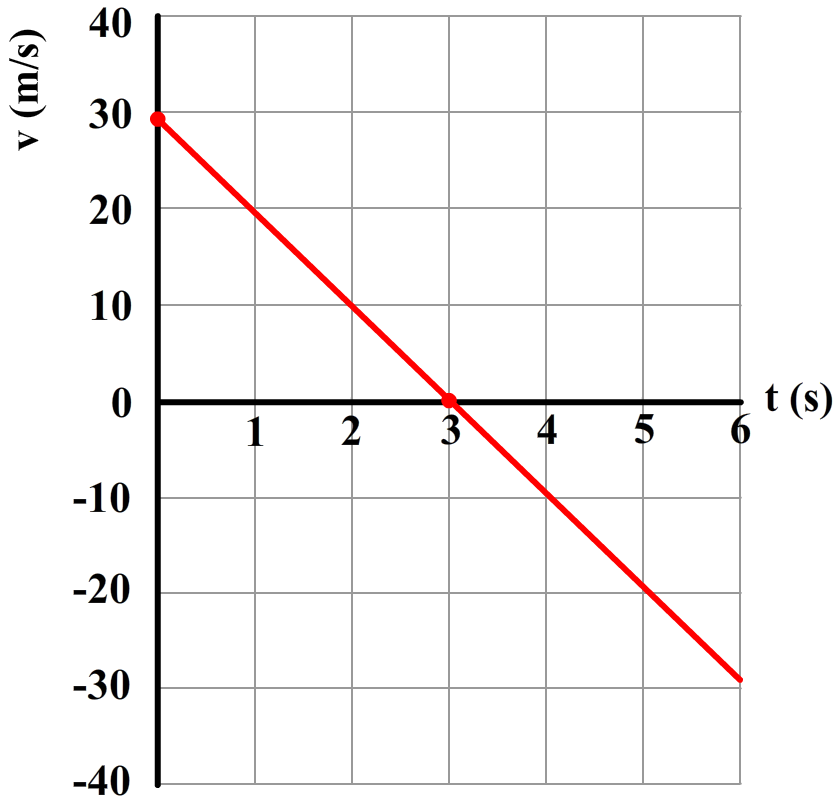
Linksonder zien we een diagram waarbij de snelheid van een voorwerp toeneemt. Er is hier dus sprake van een versnelling. Rechts neemt de snelheid juist af. Hier hebben we dus te maken met een vertraging. Let erop dat een vertraging niet betekent dat het voorwerp achteruit gaat. In dit geval gaat het voorwerp vooruit, maar steeds langzamer!
In al deze (v,t)-diagrammen geldt:
- Hoe hoger de grafiek, hoe groter de snelheid.
Zoals je gemerkt hebt, lees je (x,t)- en (v,t)-diagrammen op een heel andere manier af. In de onderstaande afbeelding is dit nog een keer samengevat:
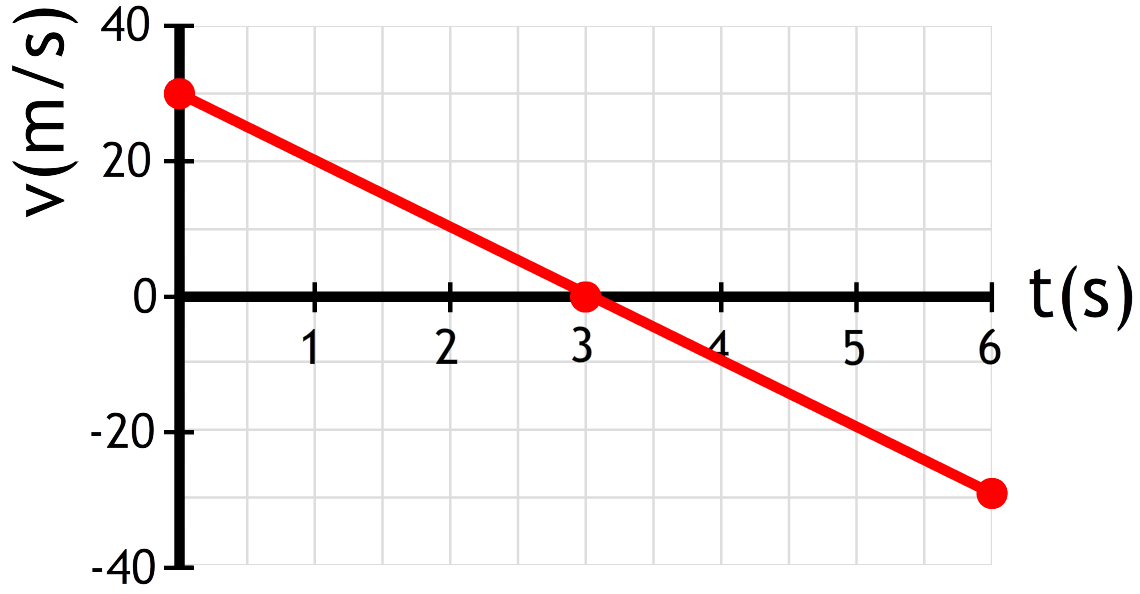
Ook achteruit bewegen geven we in een (v,t)-diagram weergeven. Dit doen we met behulp van een negatieve snelheid. In het onderstaande voorbeeld kan je leren hoe dit werkt:
 Voorbeeld
Voorbeeld
|
|
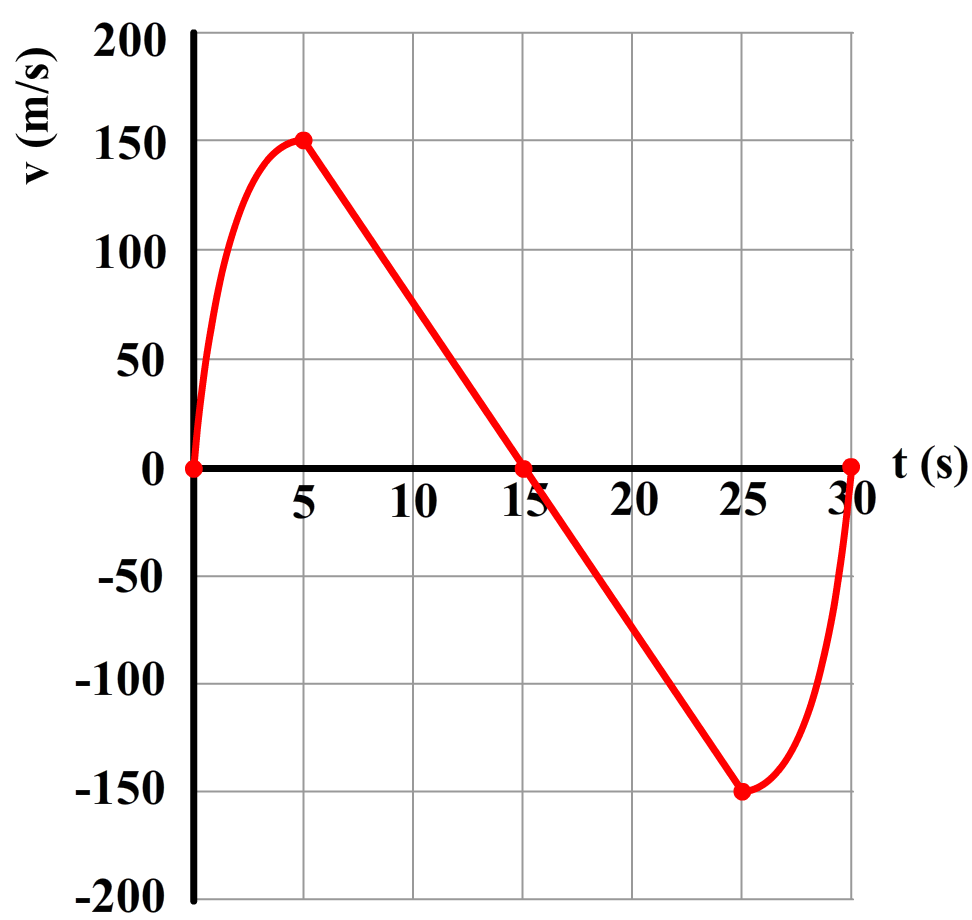
Vraag: In het rechter (v,t)-diagram zien we de beweging van een bal die omhoog gegooid wordt en daarna weer naar beneden valt. Beschrijf deze beweging in detail.
Antwoord: In de eerste drie seconden neemt de snelheid af. We hebben hier dus te maken met een vertraging. De snelheid is positief, dus de bal beweegt hier omhoog. Op t = 3,0 s is de snelheid even 0 m/s. Op dit punt staat de bal dus een moment stil. De bal bevindt zich hier op zijn hoogste punt. In de laatste drie seconden wordt de snelheid negatief. Hier beweegt de bal dus naar beneden. De snelheid neemt hier toe in negatieve richting. De bal is hier dus naar beneden aan het versnellen.
|
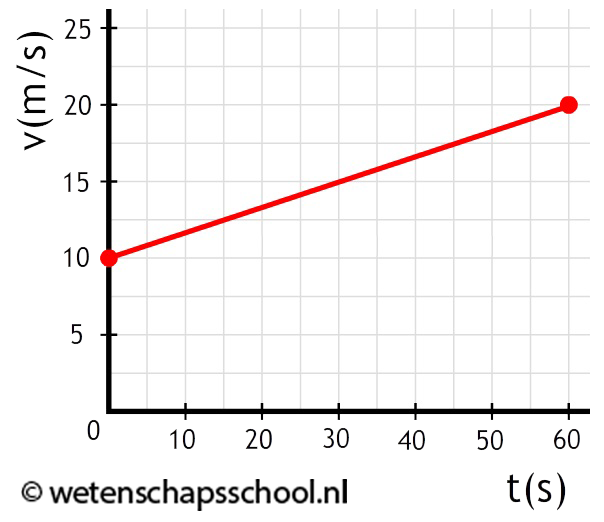
Met een (v,t)-diagram kunnen we ook de gemiddelde versnelling bepalen. In het onderstaande diagram is de toename van de snelheid Δv gelijk aan 4,0 m/s. De tijdsduur Δt van de beweging is 6,0 seconden. De gemiddelde versnelling is dus:
$$ a_{gem} = \frac{\Delta v}{\Delta t} $$ $$ a_{gem} = \frac{4,0}{6,0} = 0,67 \text{ m/s}^2$$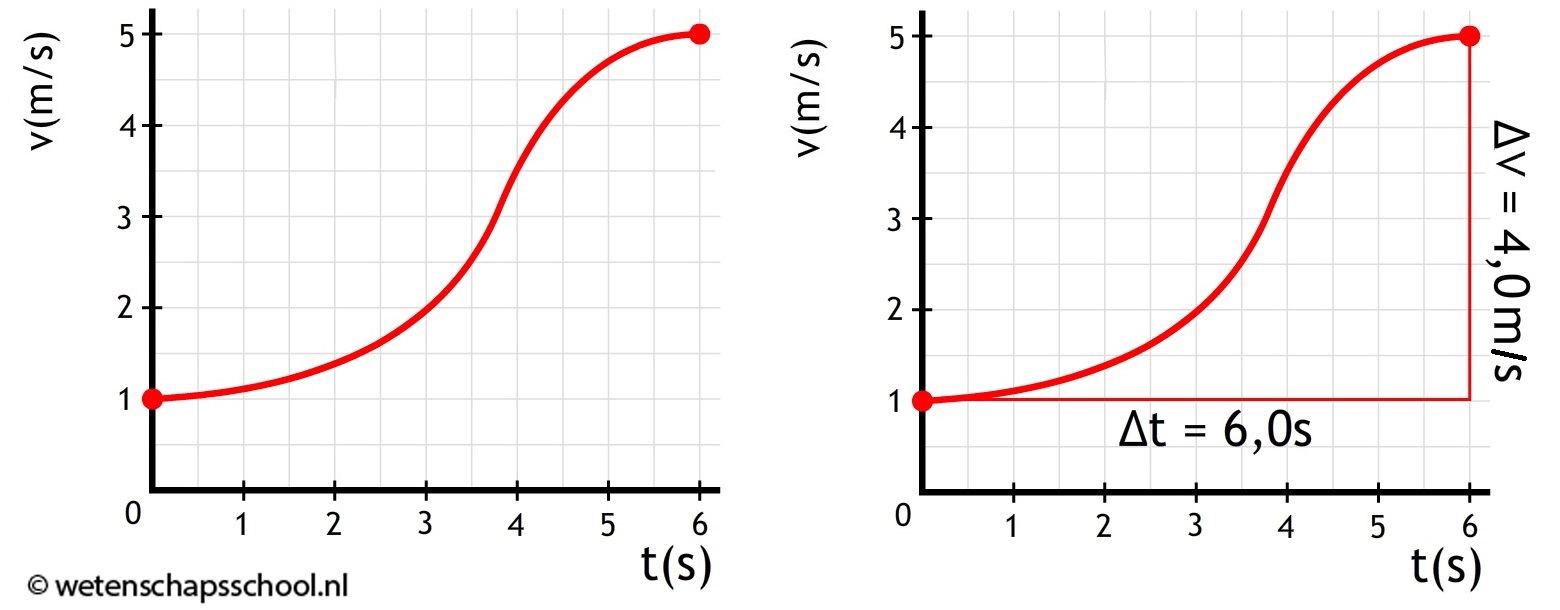
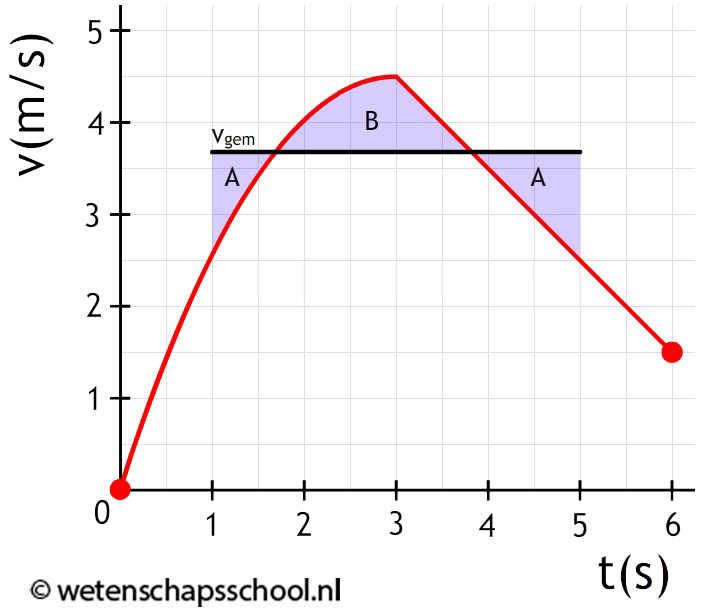
De gemiddelde snelheid is ook te bepalen met behulp van een (v,t)-diagram. Stel dat we bijvoorbeeld de gemiddelde snelheid willen weten van de onderstaande beweging van tijdstip t = 1,0 s tot t = 5,0 s. We trekken hiervoor een horizontale lijn, waarbij oppervlaktes boven de grafiek maar onder de lijn (A) gelijk zijn aan oppervlaktes onder de grafiek maar boven de lijn (B). Deze lijn geeft dan de gemiddelde snelheid aan. In dit geval is de gemiddelde snelheid 3,7 m/s.
We kunnen in een (v,t)-diagram ook de versnelling op één moment bepalen. Dit doen we met behulp van een raaklijn (zie de vorige paragraaf). De formule voor de versnelling wordt in dat geval:
$$ a = \frac{dv}{dt} $$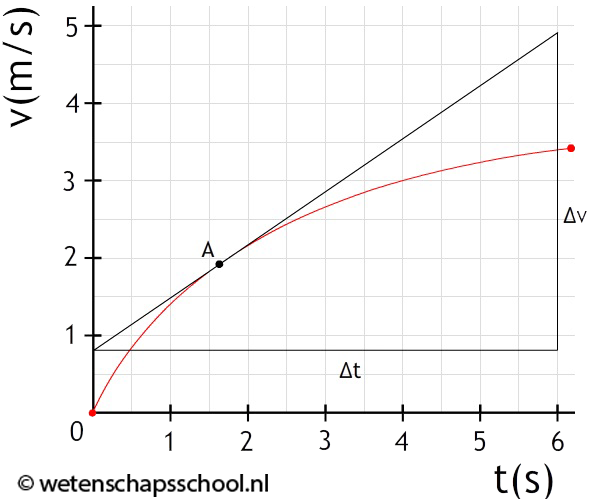
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|
§5 De oppervlaktemethode
In deze paragraaf gaan we een techniek leren waarmee we de verplaatsing kunnen bepalen met behulp van (v,t)-diagrammen. We noemen dit de oppervlaktemethode.
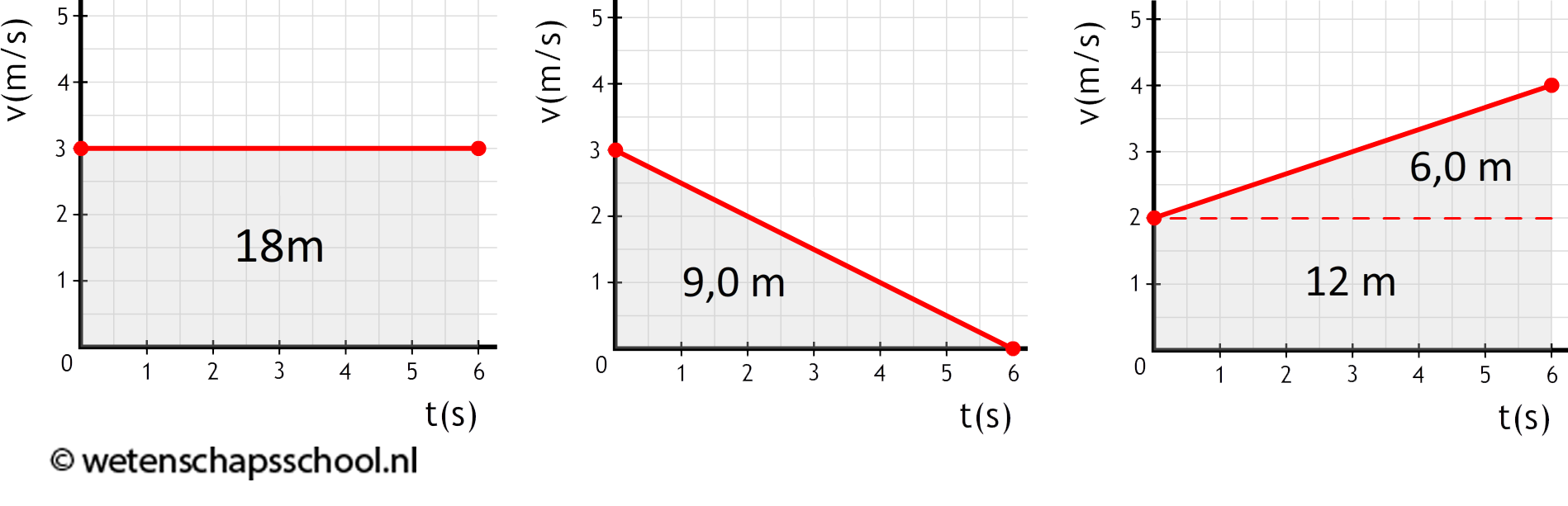
We kunnen met een (v,t)-diagram ook de verplaatsing van een voorwerp bepalen. De oppervlakte onder een (v,t)-grafiek blijkt namelijk gelijk te zijn aan de verplaatsing (Δx) van het voorwerp. In het linker onderstaande diagram is het oppervlak gelijk aan 6,0 × 3,0 = 18 m. Het voorwerp heeft hier dus 18 meter afgelegd. In het middelste voorbeeld is het oppervlak een driehoek gelijk aan (6,0 × 3,0)/2 = 9,0 m. Dit voorwerp heeft dus 9 meter afgelegd. In de rechter afbeelding bestaat het oppervlak onder de grafiek uit een rechthoek en een driehoek. Het oppervlak geeft een verplaatsing van 2 × 6 + (2 × 6)/2 = 18 m.
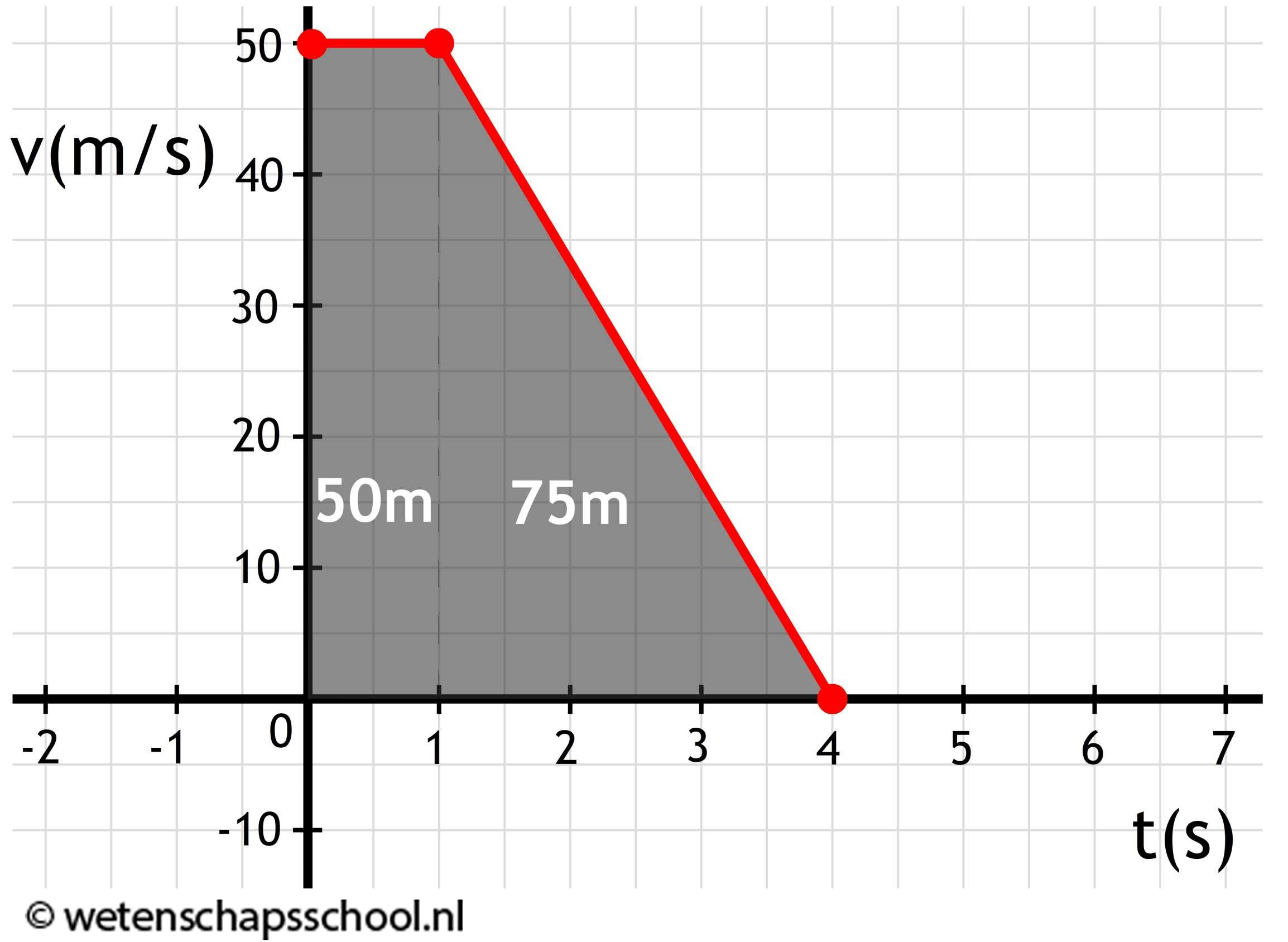
Hieronder zien we het (v,t)-diagram van een remmend voertuig. Op tijdstip t = 0 s springt een stoplicht op rood. Zoals je in het diagram kunt zien, duurt het nog 1,0 seconde voordat de bestuurder hierop reageert door op zijn rem te trappen. De reactietijd van de bestuurder is dus 1,0 seconde. Na de reactietijd duurt het in dit voorbeeld nog 3 seconden voordat het voertuig stil staat.
De afstand die het voertuig gedurende de reactietijd aflegt noemen we de reactieafstand. In dit geval is dit 50 × 1 = 50 m. De afstand die het voertuig tijdens het remmen aflegt noemen we de remweg. In dit geval is dat (50 × 3)/2 = 75 m. De reactieafstand en de remweg samen noemen we de stopafstand. In het bovenstaande voorbeeld is de stopafstand gelijk aan 50 + 75 = 125 m.
 Voorbeeld
Voorbeeld
|
|
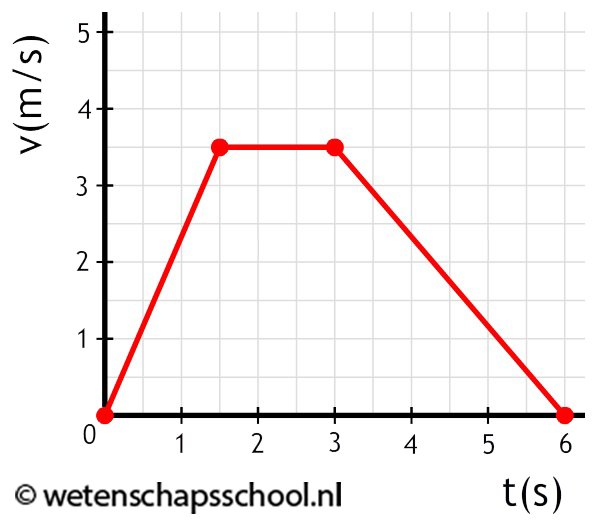
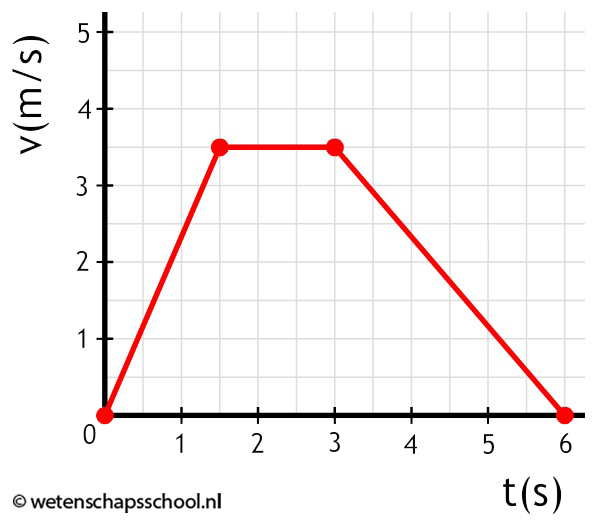
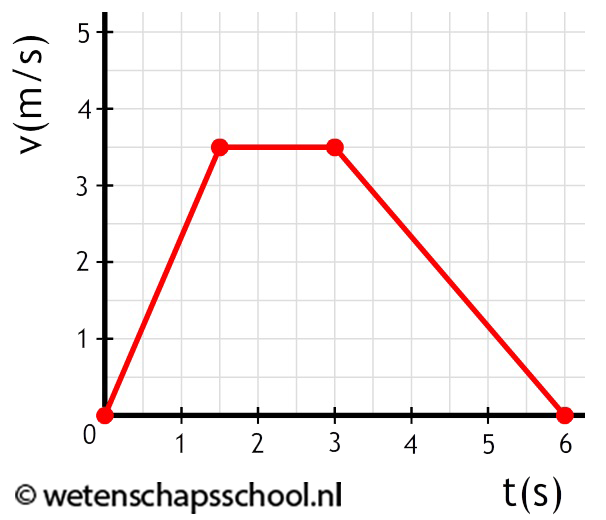
Opdracht: Bereken de gemiddelde snelheid van de volgende beweging:
Antwoord: Het oppervlak onder de grafiek is gelijk aan de verplaatsing (Δx). Het oppervlak is: $$ \frac{1,5 \times 3,5}{2} + 1,5 \times 3,5 + \frac{3 \times 3,5}{2} = 13,1 \text{ m} $$In de grafiek zien we dat de beweging 6,0 seconden geduurd heeft. Met deze gegevens kunnen we de gemiddelde snelheid berekenen: $$v_{gem} = \frac{\Delta x}{\Delta t} = \frac{13,1}{6,0} = 2,2 \text{ m/s}$$De gemiddelde snelheid is dus 2,2 m/s.
|
In sommige gevallen kunnen we het oppervlak onder de grafiek niet met een simpele formule bepalen. In dat geval is het nodig om de hokjes onder de grafiek te tellen. In het onderstaande voorbeeld laten we zien hoe dit moet.
 Voorbeeld
Voorbeeld
|
|
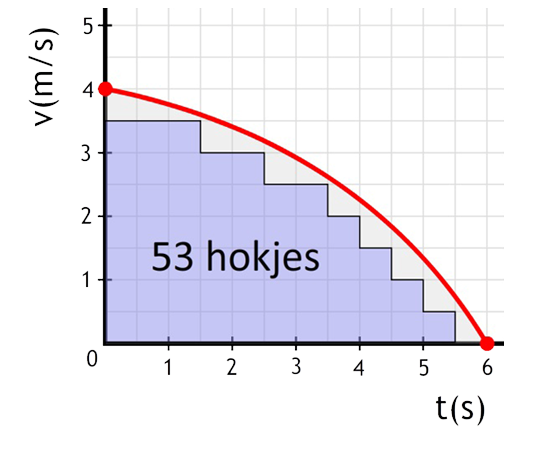
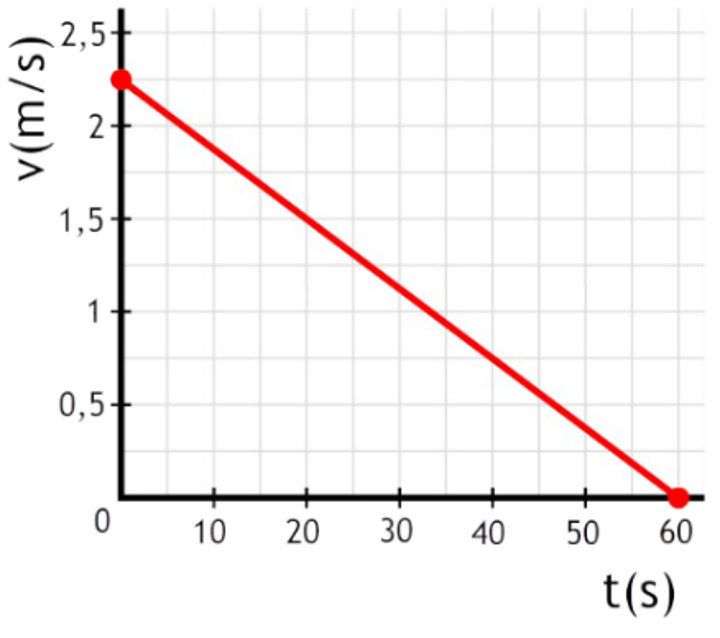
Vraag: In het linker onderstaande (v,t)-diagram wordt het remmen van een voertuig beschreven. Bepaal hoeveel meter het voertuig heeft afgelegd tijdens het remmen.
Antwoord: De afgelegde afstand tijdens het remmen is gelijk aan het oppervlak onder de grafiek. We gaan dit bepalen door hokjes te tellen. In de onderstaande afbeelding is te zien dat er 53 hele hokjes onder de grafiek te vinden zijn.
Bij het overgebleven oppervlak moeten we zo goed mogelijk schatten hoeveel hokjes dit zijn. Ga zelf na dat dit ongeveer 9,5 hokjes zijn (in het onderstaande filmpje laat ik precies zien hoe je dit kan doen). In totaal hebben we dus 53 + 9,5 = 62,5 hokjes. Elk hokje heeft een oppervlak van 0,5 × 0,5 = 0,25 m. De totale verplaatsing is dus: $$ \Delta x = 62,5 \times 0,25 = 15,6 \text{ m} $$
|
 Leerdoelen:
Leerdoelen:
|
|
 Opdrachten
Opdrachten
|
|