Hoofdstuk 9
Warmte
§1 Temperatuur §2 Faseovergangen §3 Warmtetransport
§1 Temperatuur
In dit hoofdstuk gaan we fenomenen in de wereld om ons heen verklaren aan de hand van de beweging van kleine deeltjes waaruit de wereld bestaat. We noemen deze kijk op de wereld het deeltjesmodel. In deze eerste paragraaf gaan we de luchtdruk en de temperatuur op deze manier bestuderen.
De wereld bestaat uit kleine deeltjes die we atomen noemen. Hoewel atomen een miljoen keer kleiner zijn dan een millimeter, kunnen we ze tegenwoordig met goede microscopen wel waarnemen (zie de onderstaande afbeelding). Veel fenomenen in de wereld om ons heen zijn te verklaren aan de hand van de beweging van deze atomen. We noemen deze methode om de wereld te begrijpen het deeltjesmodel.

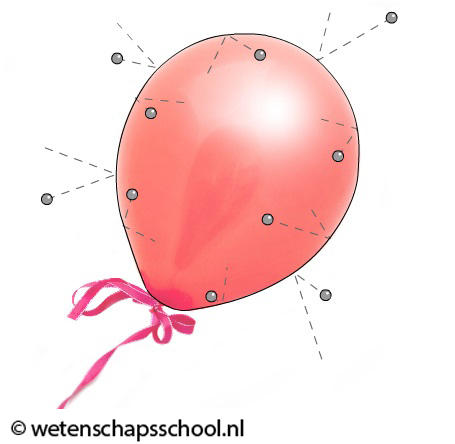
Een toegankelijk voorbeeld hiervan is de luchtdruk. De luchtdruk wordt veroorzaakt door het botsen van de miljarden deeltjes waaruit de lucht bestaat. We kunnen het effect van deze botsingen goed zien bij een opgeblazen ballon. Als je een ballon opblaast, dan pers je een hele hoop deeltjes de ballon in. Als een ballon opgeblazen is, dan is de kracht die de deeltjes op de binnenwand uitoefenen groter dan de kracht die de deeltjes op de buitenwand uitoefenen.
Ook de temperatuur kunnen we met het deeltjesmodel begrijpen. Zoals je weet meten we de temperatuur met een thermometer. Een veelgebruikte thermometer bestaat uit een dun buisje met daarin gekleurde alcohol (zie de onderstaande afbeelding). Als de alcohol warmer wordt, dan zet het uit, waardoor het alcoholniveau stijgt. Als de alcohol afkoelt, dan krimpt het, waardoor het alcoholniveau weer daalt.

De bekendste eenheid voor de temperatuur is de graden Celsius (°C). Het maken van een correcte schaal op een thermometer wordt het ijken van een thermometer genoemd. Dit doen we als volgt. Het alcoholniveau als we de thermometer in ijs steken noemen we 0 °C. Het alcoholniveau als we de thermometer in kokend water steken noemen we 100 °C. De afstand tussen deze twee niveaus kan dan in honderd gelijke stapjes van 1 °C verdeeld worden.
 Voorbeeld
Voorbeeld
|
|
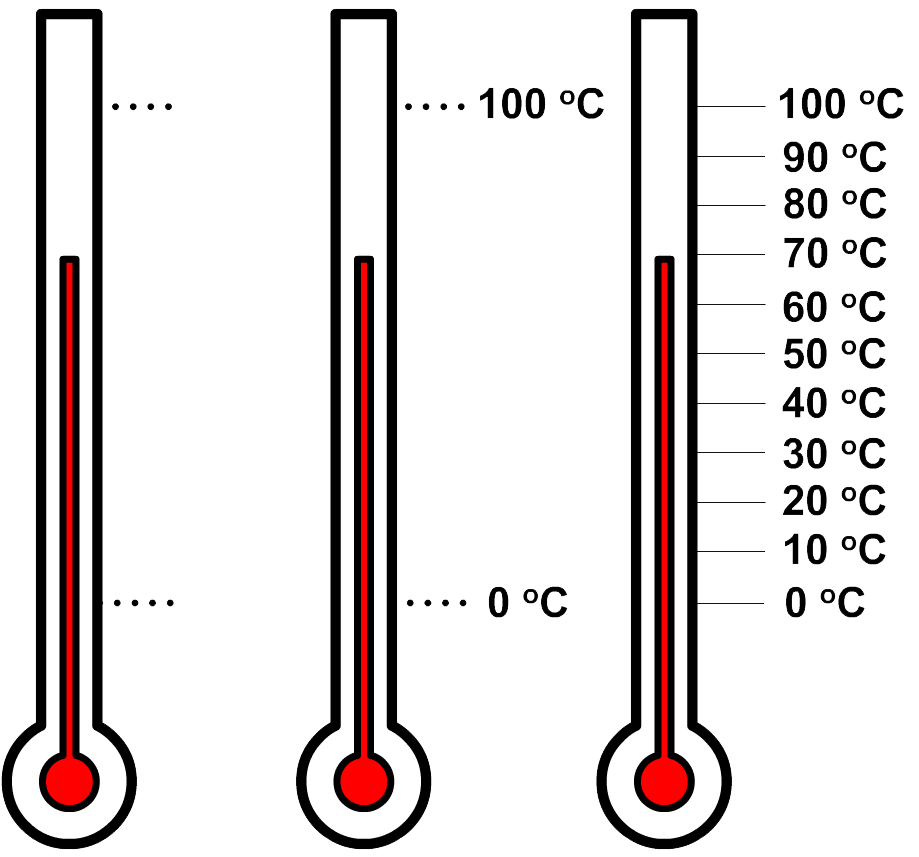
Vraag: In de onderstaande linker afbeelding zien we een ongeijkte thermometer. De onderste stippellijn werd gezet toen de thermometer in ijswater gelegd werd. De bovenste stippellijn werd gezet toen de thermometer in kokend water gelegd werd. Noteer de schaalverdeling op de thermometer in stapjes van 10 oC en bepaal daarna de temperatuur die de thermometer aangeeft. Antwoord: De onderste stippellijn geeft de temperatuur in ijswater. Dit heeft een temperatuur van 0 oC. De bovenste stippellijn geeft de temperatuur in kokend water. Dit heeft een temperatuur van 100 oC. In de tweede onderstaande afbeelding is dit toegevoegd. Meet nu de afstand tussen de stippellijnen. In dit geval vinden we 6,5 cm. Als we deze afstand door tien delen, dan vinden we de afstand behorende bij een stapje van 10 oC. In dit geval vinden we: 6,5 / 10 = 0,65 cm In de derde afbeelding zijn deze stapjes toegevoegd. We kunnen hiermee ook de thermometer aflezen. We vinden 69 oC.
|
Ook de temperatuur wordt veroorzaakt door de beweging van de deeltjes waaruit het materiaal bestaat. Hoe sneller de atomen bewegen, hoe hoger de temperatuur van het voorwerp. In het onderstaande filmpje demonsteren we dit principe door de beweging van inkt in warm en koud water te vergelijken.
Andersom geldt ook dat hoe langzamer de atomen bewegen, hoe lager de temperatuur wordt. Als we een voorwerp blijven afkoelen, dan komt er een moment dat alle atomen stil staan. Dit gebeurt bij -273 °C. Op dat moment is de allerlaagste temperatuur bereikt. We noemen deze temperatuur het absolute nulpunt. Het is niet mogelijk dat een materiaal nog kouder wordt, want de atomen staan bij deze temperatuur immers al helemaal stil.
Sinds de ontdekking van het absolute nulpunt wordt ook vaak een andere eenheid voor de temperatuur gebruikt: de kelvin (K). Bij deze schaal is ervoor gekozen om de temperatuur van het absolute nulpunt 0 kelvin te noemen. Er geldt dus:
| $$ 0 \text{ K} = -273\,^{\circ}\text{C} $$ |
Het handige van deze schaal is dat de temperatuur in kelvin altijd positief is. Het kan immers niet kouder worden dan 0 K. Een ander voordeel is dat formules vaak simpeler worden als we gebruik maken van kelvin. Om deze redenen is de kelvin de SI-eenheid voor de temperatuur. We rekenen kelvin en graden Celsius als volgt in elkaar om:
| $$ T(K) = T(\,^{\circ}\mathrm{C}) + 273 $$ |
T(K) staat voor de temperatuur in kelvin. T(°C) staat voor de temperatuur in graden Celsius.
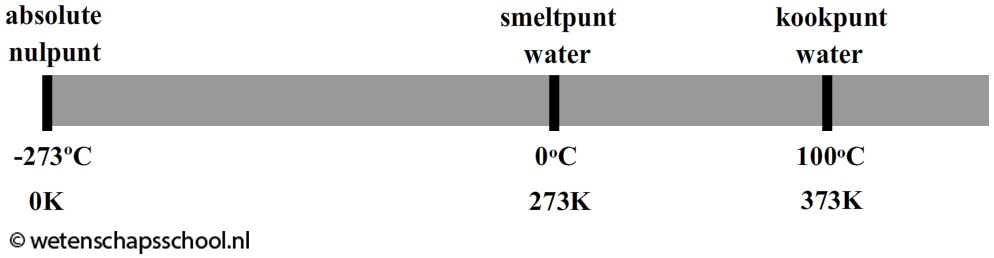
Als voorbeeld zien we hieronder het smeltpunt van water weergegeven. Water smelt bij 0 oC. Volgens de bovenstaande formules komt dit overeen met 0 oC + 273 = 273 K. Het kookpunt van water is 100 oC. Dit komt overeen met 100 oC + 273 = 373 K.
Met het deeltjesmodel kunnen we ook meteen begrijpen waarom stoffen uitzetten als we de temperatuur verhogen en krimpen als we de temperatuur verlagen. Als we de temperatuur van bijvoorbeeld een stuk metaal verhogen, dan gaan de deeltjes in dit metaal sneller trillen. Door dit trillen duwt elke atoom de omliggende atomen een beetje weg. Het materiaal neemt op deze manier meer ruimte in (zie de onderstaande animatie). Als gevolg wordt de dichtheid van het materiaal juist kleiner.
In het onderstaande filmpjes zien we dit effect in de praktijk:
In veel praktische situaties moeten we rekening houden met deze uitzetting. Bij veel bruggen zien we bijvoorbeeld een "ritssluiting" (zie de linker onderstaande afbeelding). Dit zorgt ervoor dat de brug ruimte heeft om een beetje uit te zetten op een warme dag. In de rechter afbeelding zien we wat er gebeurt als er niet goed wordt nagedacht over de uitzetting van materialen. De rails in de afbeelding zijn helemaal kromgetrokken door het uitzetten.

 (Afbeelding: Matt H. Wade; CC BY-SA 3.0 / PD)
(Afbeelding: Matt H. Wade; CC BY-SA 3.0 / PD)
 Zorg dat je kelvin en graden Celsius in elkaar kan omrekenen, dat je een thermometer kan ijken en dat je kan redeneren met deeltjesmodel
Zorg dat je kelvin en graden Celsius in elkaar kan omrekenen, dat je een thermometer kan ijken en dat je kan redeneren met deeltjesmodel
|
|
 Zorg dat je het uitzetten en krimpen van stoffen kan beschrijven op atomair niveau
Zorg dat je het uitzetten en krimpen van stoffen kan beschrijven op atomair niveau
|
|
§2 Faseovergangen
In deze paragraaf gaan we fasen en faseovergangen begrijpen met het deeltjesmodel.
Stoffen bevinden zich meestal in één van de volgende drie fasen:
- gas
- vloeibaar
- vast
We kennen allemaal de drie fasen van water. Vast water noemen we ijs, vloeibaar water noemen we gewoon "water" en water in gasvorm noemen we waterdamp.
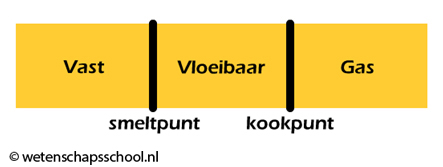
Een stof is vast als de temperatuur onder het smeltpunt ligt. Een stof is vloeibaar als de temperatuur tussen het smeltpunt en het kookpunt ligt en een stof is gasvormig als de temperatuur boven het kookpunt ligt (zie de onderstaande afbeelding).
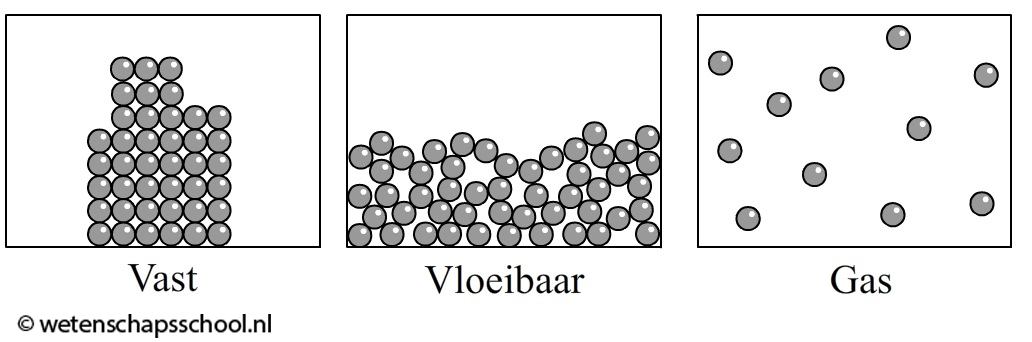
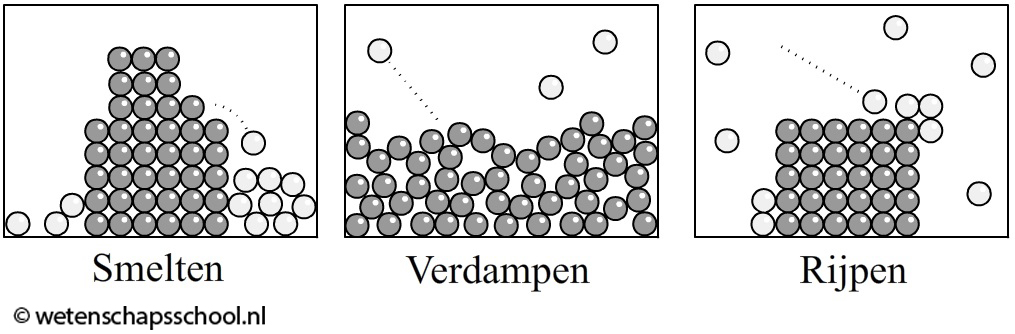
Ook de drie fasen kunnen we met het deeltjesmodel begrijpen. Hieronder zien we de drie fasen op atomair niveau afgebeeld. In de onderstaande linker afbeelding is een vaste stof op atomair niveau afgebeeld. De atomen in een vaste stof zitten op een vaste plaats en kunnen op deze plaats alleen een beetje heen en weer trillen. Alleen bij 0 K staan de deeltjes helemaal stil.
Bij een vloeistof zitten de atomen nog steeds tegen elkaar aan, maar hebben ze geen vaste plek meer. Ze kunnen nu vrij langs elkaar heen bewegen (zie de middelste afbeelding). Dit verklaart de beweeglijkheid van vloeistoffen. In een gas zijn de atomen helemaal los van elkaar en vliegen kriskras door elkaar heen (zie de rechter afbeelding). Als een gas kleurloos is (wat bijvoorbeeld bij lucht het geval is), dan kan je het niet zien. De individuele deeltjes zijn immers te klein om met het oog waar te nemen.
In het onderstaande filmpje worden de drie fasen gemodelleerd met kleine balletjes die in trilling worden gebracht. Ook wordt hier gedemonstreert waarom je een gas gemakkelijk kan indrukken.
Als een stof van één fase overgaat naar een andere, dan spreken we van een faseovergang. Hieronder zien we links het smelten van ijs. Dit is een faseovergang van vast naar vloeibaar. Zelfs een voorwerp zo hard als staal wordt bij hogere temperaturen een vloeistof (zie de middelste afbeelding). In de rechter afbeelding "zien" we water verdampen. Dit is een overgang van vloeibaar naar gas. Merk op dat de nevel die boven het kokende water ontstaat, bestaat uit kleine druppels in vloeibare fase. Pas als deze druppels lijken te verdwijnen "in het niets", veranderen ze in een gas. Waterdamp kunnen we immers niet met het oog zien.


 (Afbeelding: Pixabay; PD / P sakthy; CC BY-SA 3.0 / Pixabay; PD-mod)
(Afbeelding: Pixabay; PD / P sakthy; CC BY-SA 3.0 / Pixabay; PD-mod)
Er bestaan zes verschillende faseovergangen. De namen van deze overgangen kan je vinden in de onderstaande afbeelding:
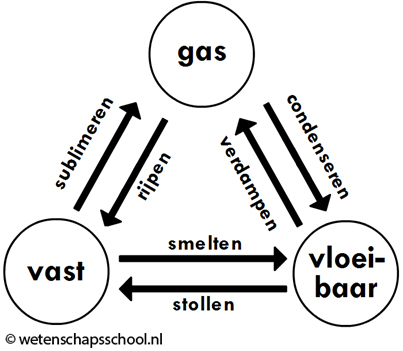
Als een vloeistof in een vaste stof verandert, dan noemen we dit stollen (het stollen van water noemen we ook wel bevriezen). Als een vaste stof in een vloeistof verandert, dan noemen we dit smelten. Water stolt als we het afkoelen onder de 0 °C en smelt als we het verwarmen boven de 0 °C. We noemen 0 °C daarom het smeltpunt of het stolpunt van water. Verschillende stoffen hebben een verschillend smeltpunt.
Als een vloeistof in een gas verandert, dan noemen we dit verdampen. Als een gas in een vloeistof verandert, dan noemen we dit condenseren (of condensatie). Water verdampt als we het verwarmen boven de 100 °C en condenseert als we het afkoelen onder de 100 °C. We noemen 100 °C daarom het kookpunt van water. Verschillende stoffen hebben een verschillend kookpunt. Condensatie treedt bijvoorbeeld op in de linker onderstaande afbeelding. Waterdamp in de lucht komt in aanraking met de koude fles en op deze manier ontstaan waterdruppeltjes aan de buitenkant van de fles. Ook dauw en mist ontstaan door condensatie (zie de twee rechter afbeeldingen).


 (Afbeelding: Acdx; CC BY-SA 3.0 / Taro Taylor; CC BY 2.0 / Hillebrand Steve; PD)
(Afbeelding: Acdx; CC BY-SA 3.0 / Taro Taylor; CC BY 2.0 / Hillebrand Steve; PD)
Als een gas in een vaste stof verandert, dan noemen we dit rijpen. Als een vaste stof in een gas verandert, dan noemen we dit sublimeren. Als het in de winter vriest, dan kan de waterdamp uit de lucht direct bevriezen. Bij het rijpen van water ontstaan kleine ijskristalletjes (zie de onderstaande afbeeldingen). De ijskristallen in de vrieskist zijn ook door rijpen ontstaan. Sublimeren komt minder vaak voor. Tijdens droge winterdagen zien we soms sneeuw verdwijnen, terwijl het de hele dag heeft gevroren. Sneeuw is in dat geval gesublimeerd tot waterdamp.

 (Afbeelding: Robert Reisman; CC BY 3.0 / Rubelson; CC BY-SA 4.0)
(Afbeelding: Robert Reisman; CC BY 3.0 / Rubelson; CC BY-SA 4.0)
Ook faseovergangen kunnen we met het deeltjesmodel beschrijven. Als we de vaste stof verwarmen, dan gaan de deeltjes steeds harder trillen. Als het smeltpunt bereikt is, dan trillen de deeltjes zo hard dat ze niet meer op hun vaste plek kunnen blijven zitten. Hoewel de deeltjes nog steeds dicht tegen elkaar aan liggen, beginnen ze nu langs elkaar te bewegen. Als dit gebeurt, is het materiaal aan het smelten en ontstaat er een vloeistof. Als we de stof nog verder verwarmen, dan bereiken we op een gegeven moment het kookpunt. Bij het kookpunt bewegen de deeltjes zo snel dat ze ontsnappen uit de vloeistof. Als dit gebeurt, is het materiaal aan het verdampen en ontstaat er een gas.
 Zorg dat je kan redeneren met faseovergangen en met het smelt- en kookpunt
Zorg dat je kan redeneren met faseovergangen en met het smelt- en kookpunt
|
|
§3 Warmtetransport
In deze paragraaf gaan we het hebben over het verschil tussen warmte en temperatuur en gaan we drie manieren bestuderen waarop warmte kan stromen van de ene plek naar de andere.
Stel je legt een stuk ijzer met een temperatuur van 60 °C tegen een even groot stuk ijzer met een temperatuur van 0 °C (zie de onderstaande afbeelding). Door de hogere temperatuur trillen de deeltjes in het linker blok sneller. Deze snel trillende deeltjes in het linker blok botsen tegen de minder snelle deeltjes in het rechter blok. Als gevolg hiervan remmen de deeltjes in het linker blok wat af en gaan de deeltjes in het rechter blok juist sneller trillen. De temperatuur van het linker blok neemt hierdoor af en de temperatuur in het rechter blok neemt hierdoor toe. Dit proces gaat door totdat de deeltjes in beide stukken evenveel trillen. Dit gebeurt als de temperatuur gelijk wordt. Als er geen warmte verloren gaat aan de omgeving en als de blokken even groot zijn, dan zal de temperatuur van beide blokken uiteindelijk 30 °C worden.

Hoe harder de deeltjes in een stof trillen, hoe meer bewegingsenergie deze deeltjes hebben. In het hierboven beschreven proces is dus bewgingsenergie verplaatst van het linker naar het rechter blok. De energie die uitgewisseld wordt tussen warme en koude stoffen noemen we de warmte (Q). De SI-eenheid van de energie is joule (J). Omdat warmte ook een vorm van energie is, meten we dit ook in joule.
Het is belangrijk om onderscheid te maken tussen warmte en temperatuur. De temperatuur meten we met een thermometer en de eenheid hiervan is graden Celsius of kelvin. Warmte is een soort energie en de eenheid hiervan is de joule. Er geldt dus:
|
Temperatuur (T) |
kelvin (K) |
|
Energie (E) |
joule (J) |
|
Warmte (Q) |
joule (J) |
We hebben gezien dat in het bovenstaande voorbeeld een deel van de energie in het linker blok overgedragen is naar het rechter blok. We hebben daarom geconcludeerd dat er warmte is verplaatst van links naar rechts. In het dagelijks leven wordt in dit voorbeeld ook wel eens gezegd dat "kou" van rechts naar links is gestroomd. Het linker blok is immers kouder geworden. In de natuurkunde wordt deze manier van denken echter zo veel mogelijk vermeden. De energie stroomt immers van hoge naar lage temperatuur en niet andersom. Een zin als "doe het raam dicht, want er komt kou binnen" is natuurkundig gezien dus onhandig. Wat er in werkelijkheid gebeurt is dat er juist warmte naar buiten stroomt.
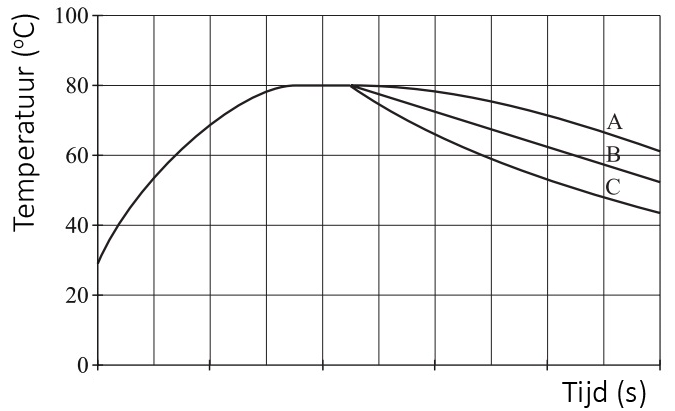
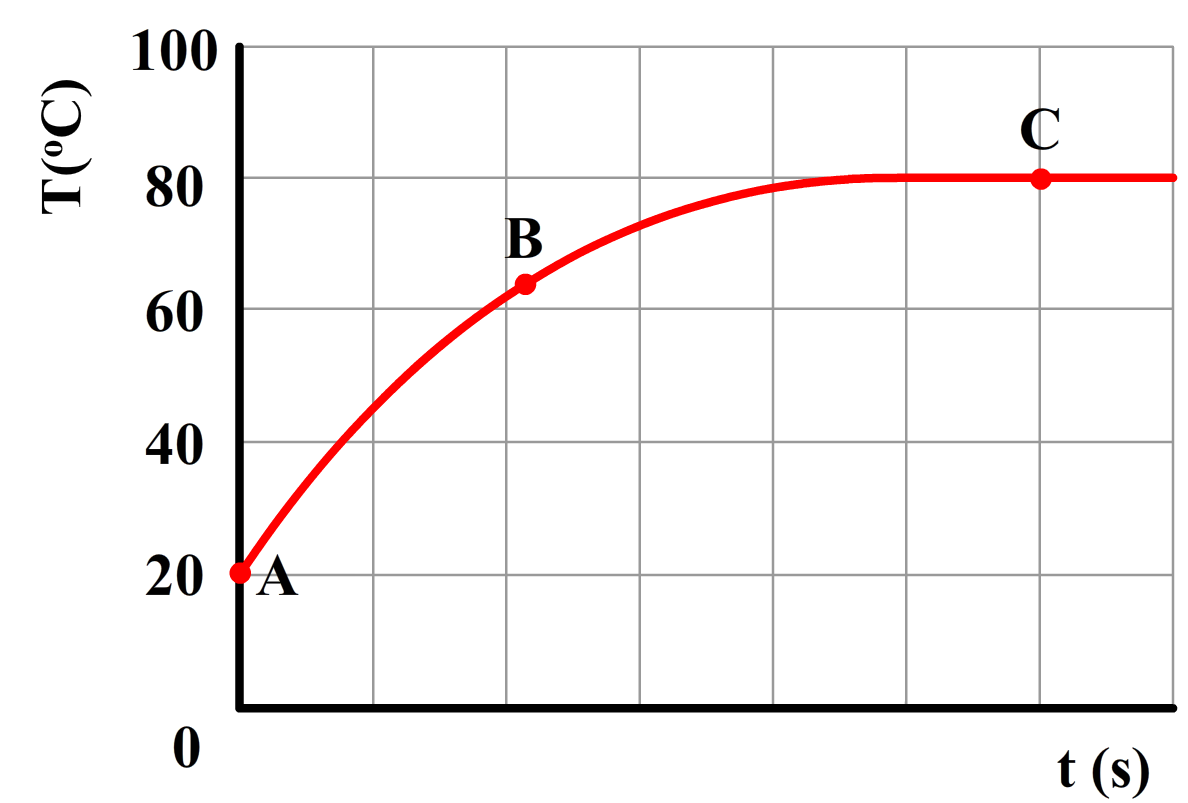
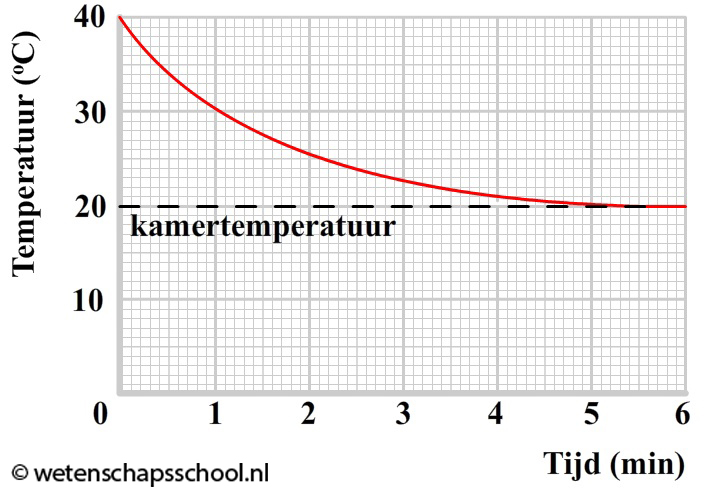
Hoeveel warmte er zal stromen van een plek met hoge temperatuur naar een plek met lage temperatuur hangt af van het temperatuurverschil (ΔT) tussen deze twee plekken. Hoe groter het temperatuurverschil, hoe meer warmte er zal stromen. We kunnen dit goed zien in het onderstaande diagram. Het diagram geeft het afkoelen van voorwerp in een kamer met een omgevingstemperatuur van 20 graden Celsius weer. Merk op dat bij een groot temperatuurverschil tussen het voorwerp en de kamer, de temperatuur van het voorwerp snel afneemt. Als de temperatuur van het voorwerp na verloop van tijd niet meer zo veel verschilt van de kamertemperatuur, dan neemt de temperatuur nog maar heel langzaam af.
Het stromen van warmte noemen we ook wel warmtetransport. Er bestaan drie soorten warmtetransport:
- Warmtegeleiding
- Warmtestroming
- Straling
Warmtegeleiding (ook wel gewoon geleiding genoemd) ontstaat doordat atomen hun warmte doorgeven doordat ze tegen elkaar botsen. Stel dat een stuk metaal op één plek wordt verwarmd. Als gevolg gaan op deze plek de deeltjes sneller trillen. Deze deeltjes botsen dan tegen omringende deeltjes en deze worden als gevolg ook in trilling gebracht. Op deze manier trekt de warmte door het materiaal. We zien dit effect bijvoorbeeld als we een metalen lepel in een pan kokend water plaatsen. De warmte trekt dan door het metaal omhoog (zie de onderstaande afbeelding).

In het onderstaande filmpje wordt de geleidbaarheid van ijzer, aluminium en koper vergeleken:
Niet alle stoffen geleiden warmte even goed. Een metalen lepel in een pan met kokend water wordt bijvoorbeeld veel sneller warm dan een houten of een plastic lepel. Metaal wordt daarom een goede geleider genoemd en hout een slechte geleider. Slechte geleiders worden ook wel isolatoren genoemd.
Ook gassen en vloeistoffen zijn isolatoren. Een thermosfles maakt bijvoorbeeld gebruik van de isolerende eigenschap van lucht. De wand van een thermosfles bestaat uit twee laagjes met daartussen lucht en als gevolg stroomt warmte lastig de fles in en lastig de fles uit. Warme dranken blijven hierdoor langer warm en koude dranken langer koud. Hetzelfde principe wordt toegepast bij dubbelglas. Dubbelglas bestaat uit twee glazen met daartussen lucht. Dit zorgt ervoor dat we weinig warmte verliezen via de ramen en als gevolg besteden we minder geld aan het opwarmen van ons huis. Ook via de muren ontsnapt warmte. Om dit te verminderen bestaan muren vaak uit twee delen met daartussen lucht. Dit worden ook wel spouwmuren genoemd.
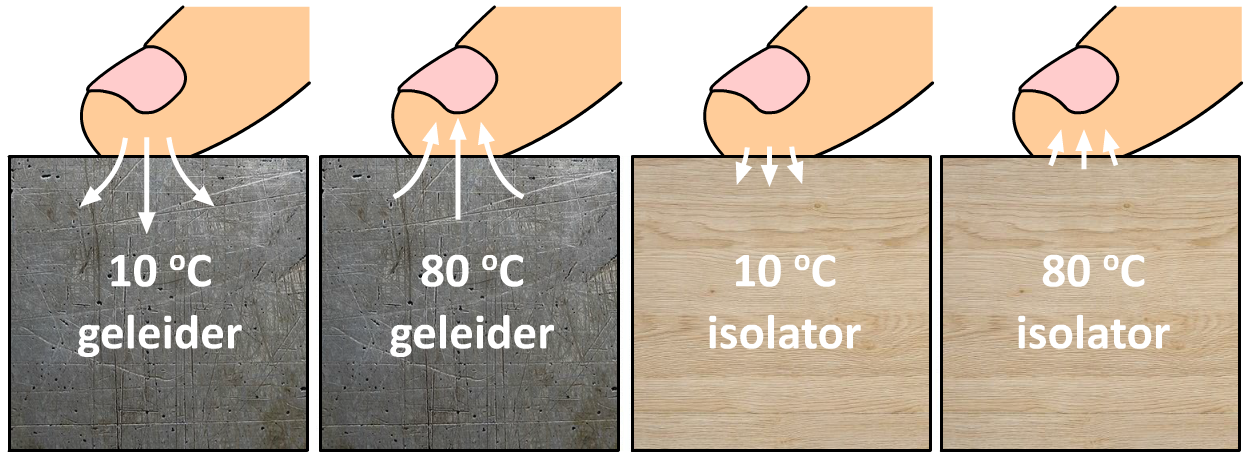
Het verschil in geleidbaarheid van verschillende stoffen kunnen we ook zien in de onderstaande afbeelding. Als je je vinger op een koude geleider legt, dan trekt de warmte van je vinger gemakking in het materiaal en wordt je vinger koud. Als gevolg zeg je dat het metaal koud aanvoelt. Als je je vinger op een hete geleider legt, dan trekt de warmte ook gemakkelijk je vinger in. Als gevolg voelt het metaal erg heet aan. Bij een isolator is de warmte-overdracht zowel bij lage als hoge temperatuur niet groot. Als gevolg voelt dit material niet snel erg heet of erg koud aan.
We zien dit effect in het onderstaande filmpje. Een ijsklontje wordt op een stuk aluminium gelegd en op een stuk hout. Het ijsklontje dat op aluminium ligt smelt sneller, omdat aluminium een goede geleider is en daardoor de warmte in het materiaal gemakkelijk naar het ijsklontje stroomt.
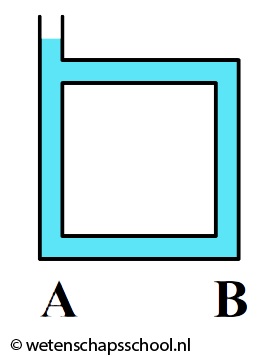
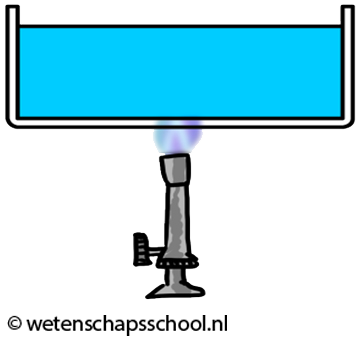
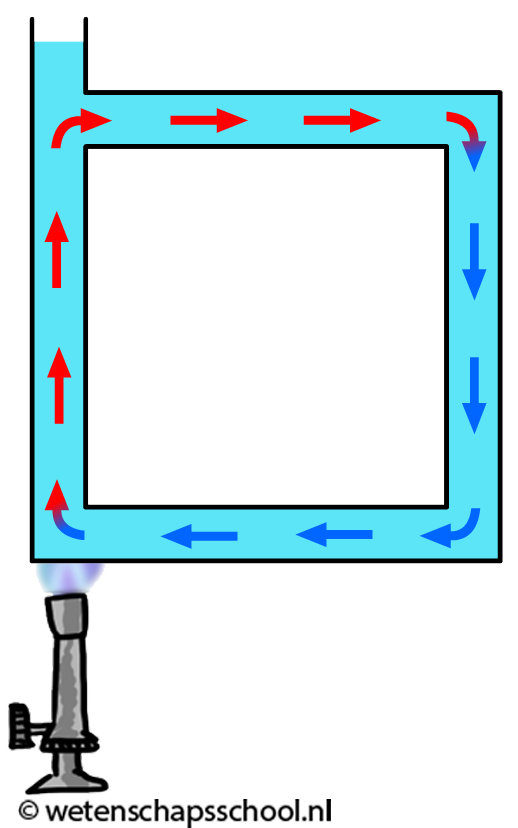
/////////// //Water of 20 degrees feels cold. Water is 26x better at conducting heat than air.Hoewel gassen en vloeistoffen geen goede geleiders zijn, kan warmte hierin wel goed worden getransporteerd met behulp van warmtestroming. We kunnen dit effect goed zien in de onderstaande linker afbeelding. Door geleiding zal het water in de buurt van de vlam opwarmen. Dit warme water zet uit en als gevolg wordt de dichtheid van het water kleiner en zal het opstijgen. Hierdoor begint het water rond te stromen.
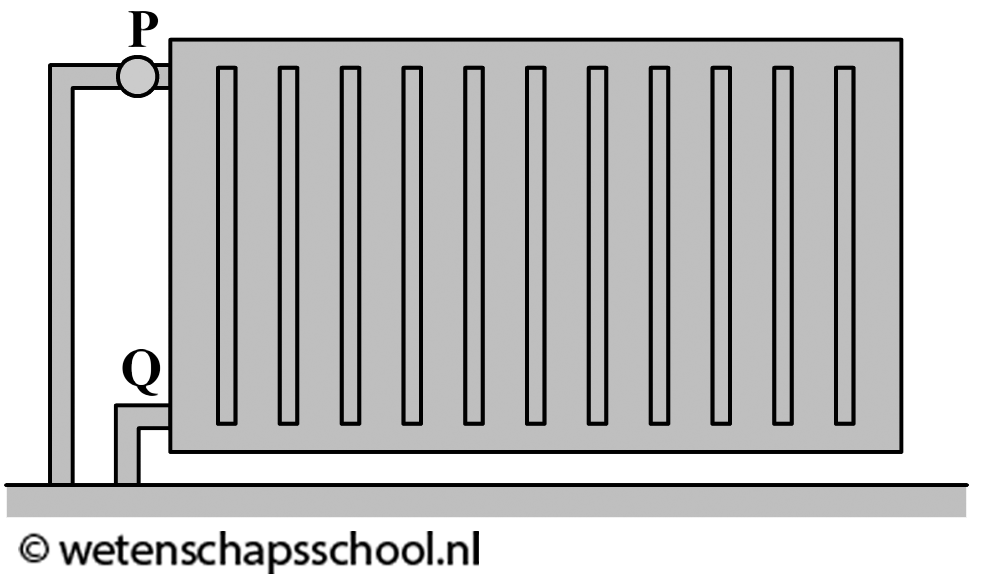
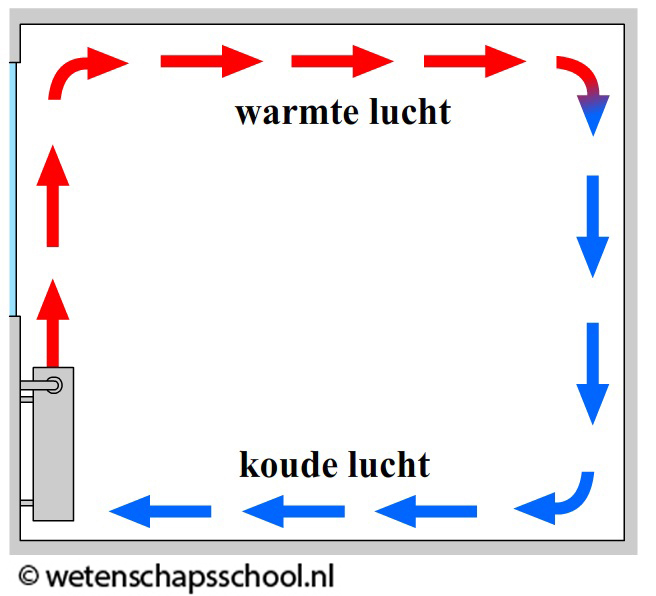
Ook het verwarmen van een kamer met behulp van een verwarming gebeurt via warmtestroming. In veel huizen wordt water opgewarmt in een cv-ketel met behulp van aardgas. Dit warme water wordt dan rondgepompt naar de verwarmingen in huis. De warme verwarmingen zorgen er weer voor dat de lucht in de kamers warm wordt (zie de onderstaande rechter afbeelding). De verwarming zelf kan met behulp van geleiding alleen de lucht verwarmen die direct in contact staat met de verwarming. Deze lucht wordt hierdoor warmer, krijgt een lagere dichtheid en stijgt op. Als gevolg ontstaat er een warmtestroom in de kamer en wordt de kamer steeds warmer.
In het onderstaande filmpje demonsteren we dit principe. De stroming is zichtbaar gemaakt met behulp van kleine aluminiumdeeltjes:
In sommige gevallen willen de warmtestroming juist beperken. Bij een spouwmuur is de binnenwand in de winter warmer als het huis verwarmd wordt. Er ontstaat dan tussen de binnen- en de buitenwand warmtestroming van lucht. Op deze manier komt de warmte van de binnenmuur redelijk gemakkelijk bij de buitenmuur aan. Dit kan worden voorkomen door isolatiemateriaal tussen de wanden te plaatsen. Een voorbeeld hiervan is glaswol of purschuim. In beide stoffen zitten kleine belletjes lucht. De aanwezigheid van lucht beperkt geleiding en omdat de lucht niet kan stromen, beperkt het ook stroming.
De derde soort warmtetransport wordt straling genoemd. Een ander woord voor straling is licht. Dat straling warmte kan overdragen weten we als we onze handen in de zon houden. Als zonlicht door onze huid wordt geabsorbeerd, wordt onze huid warmer. Hetzelfde effect treedt ook op als je je handen warmt aan een kampvuur of openhaard. Er is ook straling die we niet met onze ogen kunnen zien. Wijzelf zenden bijvoorbeeld infraroodstraling uit. In de onderstaande afbeelding is een foto gemaakt met een infraroodcamera. Zoals je ziet geeft warm water infraroodstraling af. Als je je hand naast een hete verwarming plaatst, dan kan je de infraroodstraling ook voelen (boven de verwarming is het nog warmer, maar dat komt voornamelijk door warmtestroming).
 (Afbeelding: NASA; PD)
(Afbeelding: NASA; PD)
Om verlies via straling tegen te gaan bij het verwarmen van je huis, wordt soms glanzende folie tegen de muur achter een verwarming geplakt. De infraroodstraling die van de verwarming afkomt wordt dan niet gebruikt om de muur op te warmen, maar deze straling reflecteert terug de kamer in.
Doffe en donkere voorwerpen absorberen straling het best. Deze voorwerpen worden daarom snel warm in de zon. Deze voorwerpen zenden ook weer gemakkelijk infraroodstraling uit. Als gevolg koelen deze voorwerpen ook weer snel af in de schaduw. Bij lichte en glimmende voorwerpen geldt het omgekeerde. Deze absorberen straling slecht en zenden ook weinig infraroodstraling uit. Als je een huis hebt in een warm land, dan is het handig dit huis wit te verven, zodat het binnen overdag koel blijft.
 Zorg dat je kan redeneren met de drie soorten warmtetransport
Zorg dat je kan redeneren met de drie soorten warmtetransport
|
|
§4 Verwarmen
In deze paragraaf gaan we rekenen aan warmte.
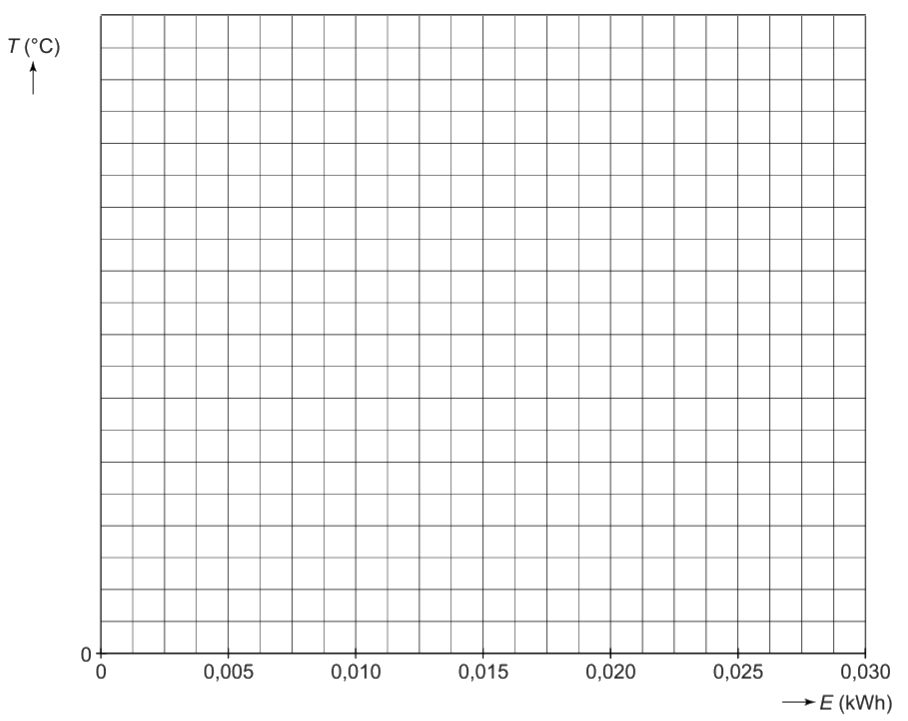
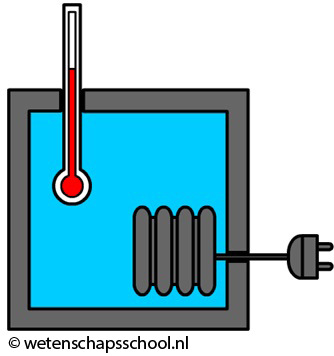
Als we willen weten hoeveel warmte er nodig is om de temperatuur van een vloeistof een bepaalde hoeveelheid te laten stijgen, dan gebruiken we daarvoor een joulemeter (ook wel calorimeter genoemd). Een joulemeter is eigenlijk niets anders dan een geïsoleerd bakje met daarin een verwarmingselement en een thermometer. In de onderstaande afbeelding zien we een joulemeter gevuld met water. In het verwarmingselement wordt elektrische energie omgezet in warmte en met deze warmte wordt het water verwarmd. Hoeveel de temperatuur van het water hierdoor stijgt, kunnen we aflezen op de thermometer.
De hoeveelheid elektrische energie die we toevoegen kunnen we uitrekenen met behulp van de spanning en de stroomsterkte. We gebruiken hiervoor eerst de volgende formule uit het hoofdstuk "Elektriciteit":
$$ P = U \times I $$
|
Ten tweede gebruiken we de formule E = Pt uit het hoofdstuk "Elektriciteit". Omdat de energie hier omgezet wordt in warmte (Q), kunnen we deze formule ook schrijven als:
$$ Q = P \times t $$
|
De elektrische energie die we met deze twee formules kunnen berekenen, zal in de joulemeter worden omgezet in warmte (Q). Als de joulemeter perfect geïsoleerd is, dan wordt alle warmte gebruikt om het water op te warmen. Met een thermometer kunnen we dan de temperatuurstijging aflezen. We kunnen op deze manier achterhalen hoeveel energie het kost om de temperatuur een graad Celsius te laten stijgen. Bij een kilogram water vindt men met dit experiment dat er 4180 joule nodig is om de temperatuur een graad Celsius te laten stijgen. Bij het maken van de opdrachten worden deze gegevens in de vraag gegeven.
Het verwarmen van een kamer met een cv-installatie die werkt op een soortgelijke manier. Hier komt de warmte echter niet uit elektrische energie, maar uit de chemische energie (Ech) die vrijkomt bij het verbranden van aardgas. In BINAS kunnen we vinden dat de verbrandingswarmte van aardgas gelijk is aan 32 J/cm3. Dit betekent dat er 32 joule aan chemische energie zit opgeslagen in één kubieke centimeter aardgas.
Deze energie wordt omgezet in warmte en hiermee wordt het huis verwarmd. Een deel van de warmte zal echter ontsnappen door de wanden van het huis. De fractie van de energie die nuttig gebruikt wordt (en dus niet verloren gaat) noemen we het rendement. Het rendement kunnen we als volgt berekenen:
| $$ \frac{E_{nuttig}}{E_{tot}} = \eta $$ |
Het rendement in deze formule is een getal tussen de 0 en de 1. Het rendement wordt ook vaak uitgedrukt als percentage. In dat geval moet het rendement uit deze formule vermenigvuldigd worden met 100. Een rendement van 0,05 komt dus overeen met een rendement van 5%.
 Voorbeeld
Voorbeeld
| ||||||||
|
Opdracht: Voor het opwarmen van een woonkamer wordt 12,0 kubieke decimeter aardgas verbrand. Bereken hoeveel energie hierbij vrijkomt. Antwoord: Volgens BINAS is de verbrandingswarmte van aardgas gelijk aan 32 J/cm3. 12,0 dm3 is gelijk aan 12 000 cm3. Met een verhoudingstabel kunnen we hiermee uitrekenen hoeveel energie er in totaal gebruikt is:
Er is dus 384 000 joule nodig om de kamer te verwarmen. Opdracht: Tijdens het verwarmen van de kamer ontsnapt 35 000 joule van de warmte door de wanden van het huis. Bereken het rendement van het verwarmen van de kamer. Antwoord: Het rendement vertelt ons hoeveel procent van de energie nuttig gebruikt is. De 35 000 J aan warmte is verloren gegaan. Er is dan 384 000 - 35 000 = 349 000 J nuttig gebruikt. Hiermee berekenen we het rendement: Enuttig = 349 000 J Etot = 384 000 J $$ \eta = \frac{E_{nuttig}}{E_{tot}} $$ $$ \eta = \frac{96200}{131200} = 0,91 $$Het rendement is dus 91%. Opdracht: Voor het verwarmen was de temperatuur van de kamer 17 oC. In de vorige vraag hebben we geleerd dat 349 000 J aan energie nuttig gebruikt wordt om de kamer op te warmen. Als de lucht 1 oC in temperatuur stijgt, neemt het 1,29 × 105 J energie op. Bereken de temperatuur van het water na het verwarmen. Antwoord: Dit lossen we weer op met een verhoudingstabel. We gebruiken dat 1 oC overeenkomt met 1,29 × 105 J aan energie:
De temperatuur is dus 2,7 oC toegenomen. We begonnen bij een temperatuur van 17 oC. De temperatuur na het verwarmen wordt 17 + 2,7 = 19,7 oC.
|
 ...
...
| ||||||||||||||||
|