Hoofdstuk 7
Het weer

§1 De druk

In dit hoofdstuk gaan we onze atmosfeer bestuderen. We gaan o.a. kijken naar de luchtdruk en de vorming van wolken. Om de luchtdruk te begrijpen, moeten we eerst het concept druk begrijpen. In deze paragraaf gaan we dit doen.

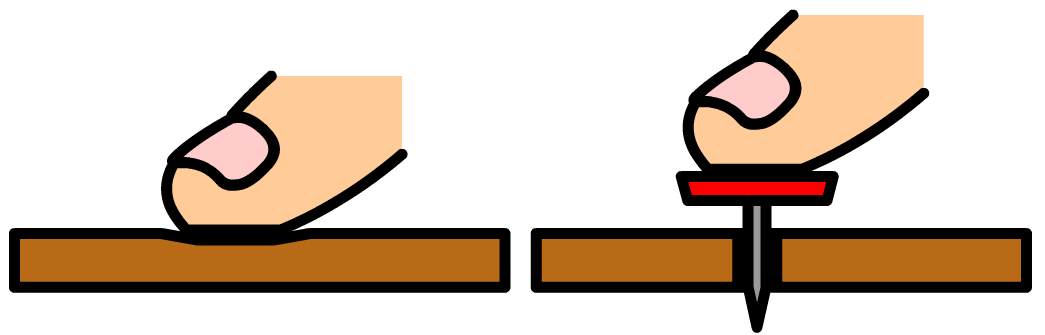
Als je met je vinger tegen een stuk karton drukt, dan gebeurt er niet zoveel. Als je echter even hard drukt met een punaise, dan prik je met gemak dwars door het karton heen (zie de onderstaande afbeelding). Hoe kan dit? Het antwoord is druk. De kracht in beide gevallen is gelijk, maar in het linker voorbeeld wordt de kracht verdeelt over een grote vingertop, terwijl bij rechts de volledige kracht wordt uitgeoefend op alleen het puntje van de punaise. De krachten zijn in beide gevallen gelijk, maar de punaise oefent een grotere druk uit.

Druk is dus gelijk aan de kracht per oppervlak. We rekenen de druk als volgt uit:

$$ p = \frac{F}{A} $$

Druk (p)

newton per vierkante meter (N/m²)
of pascal (Pa)

Kracht (F)

newton (N)

Oppervlak (A)

vierkante meter (m²)

De SI-eenheid van de druk is pascal (Pa) en dit is gelijk aan newton per vierkante meter (N/m²). Dit betekent dat je het oppervlak in vierkante meter (m²) moet invullen in de formule om het antwoord in pascal te krijgen. In veel gevallen gebruiken we voor de druk ook N/cm². In dat geval vul je het oppervlak natuurlijk in in cm².

Omdat we in een aantal gevallen de druk willen uitrekenen die de zwaartekracht (F_z) uitoefent, introduceren we ook een formule voor de zwaartekracht. Er geldt:

$$ F_{z} = m \times g $$

Zwaartekracht (F_z)

newton (N)

Massa (m)

kilogram (kg)

Valversnelling (g)

newton per kilogram (N/kg)

De massa moet in deze formule altijd gegeven worden in kilogram en de valversnelling (g) is op aarde altijd gelijk aan ongeveer 10.

Voorbeeld

Vraag:

Een blok met een massa van 25 kg wordt op de grond gezet. De onderzijde van het blok heeft een oppervlak van 30 cm². Bereken de druk die het blok op de grond uitoefent in Pa.

Antwoord:

m = 25 kg

Eerst berekenen we de zwaartekracht:
$$ F_z = mg $$ $$ F_z = 25 \times 10 = 250 \text{ N} $$
Voor de druk moeten we het oppervlak van de onderzijde van de blok eerst omrekenen naar vierkante meter:

A = 30 cm² = 0,0030 m²

Nu kunnen we de druk berekenen:
$$ p = \frac{F}{A} $$ $$ p = \frac{250}{0,0030} = 83333 \text{ Pa} $$
De druk die het blok op de grond uitoefent is dus gelijk aan 8,3 × 10⁴ Pa.

Laten we nog een paar toepassingen bespreken waarbij druk een rol speelt. Als je op ijs loopt en het ijs begint te scheuren, dan is het verstandig om op het ijs te gaan liggen en op je buik naar de kant te kruipen. Op deze manier wordt het oppervlak (A) van je lichaam in contact met het ijs groter. Volgens de formule "p = F/A" wordt de druk (p) dan kleiner. Als gevolg heb je een kleinere kans dat je door het ijs zakt.

Nog een voorbeeld. Waarom snijdt een scherp mes zoveel beter dan een bot mes? Dit komt doordat bij een scherp mes het snijoppervlak (A) kleiner is. Volgens de formule "p = F/A" wordt de druk (p) hierdoor juist groter. Als gevolg kan je met een scherp mes een veel grotere druk uitoefenen en dus kan je beter snijden.

Hieronder zien we nog twee voorbeelden. Links zien we rupsbanden om de wielen van een tank. Deze banden hebben een groot oppervlak. Dit verlaagt de druk die de tank op de grond uitoefent, waardoor de tank niet snel wegzakt in bijvoorbeeld modder. Rechts zien we rijplaten die worden neergelegd als een weg opgebroken wordt, maar de weg toch begaanbaar moet blijven voor fietsers. Fietsen over zand is niet handig. De dunne fietsbanden hebben namelijk een klein contactoppervlak en als gevolg oefenen ze een grote druk uit op het zand en zakker ze er in weg. Door rijplaten neer te leggen, wordt de zwaartekracht van de fiets en de bestuurder verdeeld over een veel groter oppervlak. Hierdoor wordt de druk kleiner en zak je dus niet meer weg.

(Afbeelding: DanielCD; CC BY-SA 3.0 / ...)

Leerdoelen:

Zorg dat je kan rekenen met de formule "p = F/A". Zorg ook dat je weet dat de SI-eenheid van de druk pascal (Pa) is en dat dit gelijk is aan N/m².

• Zorg dat je kan redeneren met druk. Zorg dat je weet dat bij gelijke kracht (F), een groter contactoppervlak (A) zorgt voor een kleinere druk (p) en een kleiner contactoppervlak (A) voor een grotere druk (p).

Opdrachten

(5p) Maak met behulp van de formule "p = F/A" duidelijk waarom:

... je op het ijs moet gaan liggen als je denkt dat het ijs gaat breken.

... het niet handig is om met hoge hakken over het strand te lopen.

... je een brood het best kan snijden met een scherp mes.

... een punaise pijn doet als je deze zelfs met een kleine kracht tegen je huid duwt.

... men rond de poolcirkel vaak loopt in sneeuwschoenen met een extreem grote zool.

(1p) In het onwaarschijnlijke geval dat een lift zou vallen, wordt aangeraden op de grond te gaan liggen. Leg dit uit.

(2p) Een hond is veilig met de auto te vervoeren in een kooi zoals in de onderstaande afbeelding is weergegeven. De kooi wordt strak tegen de achterbank vastgezet. Bij een eventuele botsing komt de hond dan met zijn zijkant tegen de brede kant van de kooi. Leg met het begrip druk uit waarom dit veilig is.

(Bron: Examen VMBO-T, 2011-1)

(3p) Als een boogschieter een pijl vaak gebruikt, dan wordt de punt stomp. Vergelijk schieten met een scherpe en een stompe punt. Neem aan dat de pijl in beide gevallen met gelijke snelheid wordt afgeschoten. Met een stompe punt is de kracht op het doelwit even groot / groter / kleiner. Met een stompe punt is het contactoppervlak met het doelwit even groot / groter / kleiner. Met een stompe punt is de druk op het doelwit even groot / groter / kleiner.

Een vat met vloeistof staat op de grond. De zwaartekracht van het vat met inhoud is 525 N. Het contactoppervlak met de ondergrond is 30,0 cm².

(2p) Bereken de druk van het vat op de ondergrond in N/cm².

(3p) Bereken de druk nu in pascal.

Een krik staat met de grondplaat op een ondergrond (zie de onderstaande afbeelding). De krik duwt een auto omhoog vanuit het steunpunt.

(2p) De kracht van de grondplaat op de ondergrond is 2300 N. Het contactoppervlak van de grondplaat met de ondergrond is 60 cm². Bereken de druk op de ondergrond in Pa.

(1p) Op een zachte ondergrond kan de krik wegzakken in de grond. Hoe kan worden voorkomen dat de krik in de grond wegzakt? Kies uit de volgende opties:
- Door het oppervlak van de grondplaat te vergroten.
- Door het oppervlak van de grondplaat te verkleinen.
- Door het oppervlak van het steunpunt te vergroten.
- Door het oppervlak van het steunpunt te verkleinen.

(Bron: Examen VMBO-T, 2023-2)

Met een riementang kan je gaten in riemen maken. Een leerling maakt en gat in zijn riem met een kracht van 35 N.

(2p) De snijbuis heeft een contactoppervlak van 0,050 cm² met de riem. Bereken de druk onder het contactoppervlak.

(1p) In een andere riem wil de leerling een groter gat maken. Wat is het gevolg voor de benodigde spierkracht? Is deze kracht groter, kleiner of blijft de kracht gelijk? Leg je antwoord uit.

(Bron: Examen VMBO-T, 2021-2)

(3p) De massa van een cheeta is 45 kg. Het totale contactoppervlak van de poten van de cheeta met de ondergrond is 140 cm². Bereken de druk op de ondergrond.
(Bron: Examen VMBO-T, 2022-1)

Een zware bloempot wordt op een tafel gezet. De pot heeft een massa van 40 kg en het contactoppervlak aan de onderzijde van de pot is 1,0 dm².

(4p) Bereken de druk die de pot op de tafel uitoefent in N/cm².

(3p) Bereken de druk nu in Pascal.

(5p) Een kleine kubus met een massa van 250 gram heeft zijden van 5,0 cm lang. Bereken de druk die het blokje op de grond uitoefent in N/cm².

(5p) Een spijkerbed bestaat uit honderden spijkers die met de punt omhoog uit een plank hout steken. De punt van elke spijker heeft een oppervlak van 0,126 mm². Een persoon met een massa van 70 kg gaat op het spijkerbed liggen en komt hierbij op 300 van de spijkers te liggen. Bereken de druk die de spijkers uitoefenen op de persoon in N/mm².

(4p) Trek je schoenzool over op een ruitjespapier en bereken de druk die je uitoefent als je op één been op de grond staat.

De druk van het gas in de volle gasfles is 40 N/cm².

(1p) Noteer deze druk in N/m².

(2p) De aansluiting van de drukregelaar in de fles heeft een oppervlak van 0,25 cm². Bereken de kracht van het gas op de aansluiting.

(Bron: Examen VMBO-T, 2018-1)

§2 De luchtdruk (GEEN CE-STOF)

In deze paragraaf gaan we het concept druk uit de vorige paragraaf gebruiken om de luchtdruk te begrijpen.

Ook gassen oefenen druk uit. Het bekendste voorbeeld hiervan is de luchtdruk. De luchtdruk ontstaat door het botsen van de deeltjes waaruit de lucht bestaat. De luchtdruk is groter dan mensen vaak denken. Lucht heeft een kleine dichtheid, maar de volledige massa van alle lucht boven ons hoofd is behoorlijk groot. In de afbeelding hieronder zien we de lucht die zich boven één vierkante meter aardoppervlak bevindt. We noemen dit een luchtkolom. De massa van alle lucht in deze kolom is 10 130 kg!

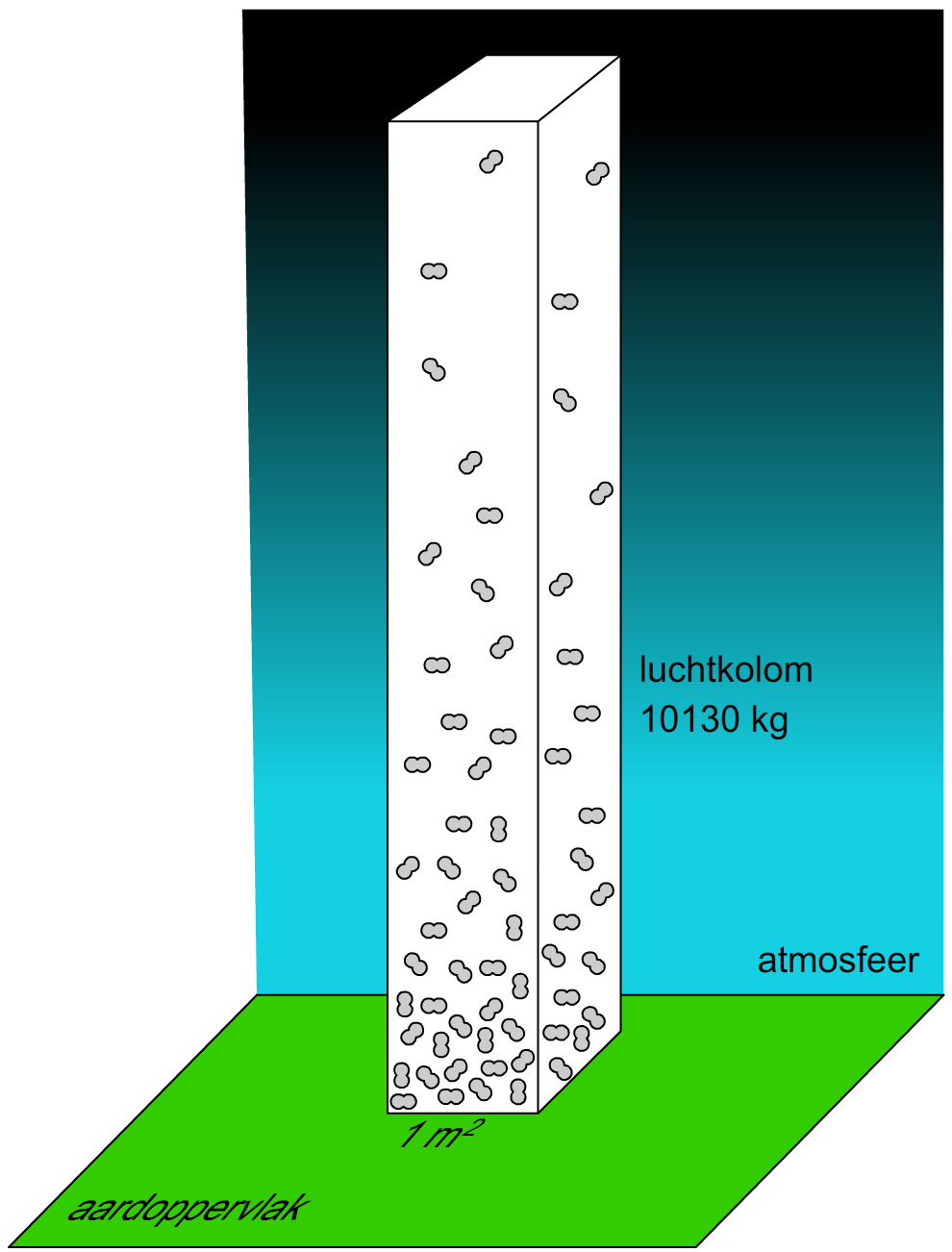
Met deze gegevens kunnen we luchtdruk op zeeniveau uitrekenen. Eerst rekenen we de zwaartekracht van de lucht uit:

$$ F_z=mg $$ $$ F_z= 10 130 \times 10 = 101 300 \mathrm{\ N} $$

En hiermee berekenen we de luchtdruk:

$$ p = FA $$ $$ p = 101 300 \times 1,0 = 101 300\ \mathrm{Pa} $$

De luchtdruk is dus gelijk aan 101 300 Pa.

In het dagelijks leven merken we relatief weinig van de hoge luchtdruk. Dit komt doordat de luchtdruk zichzelf meestal in evenwicht houdt. De luchtdruk die bijvoorbeeld op de bovenkant van je arm werkt, is even groot als de luchtdruk die op de onderkant van je arm werkt.

De grootte van de luchtdruk wordt wel merkbaar in het volgende experiment. In de onderstaande linker afbeelding zien we twee halve bollen die losjes tegen elkaar aangelegd zijn. We noemen dit de Maagdenburger halve bollen. De lucht van buiten drukt de halve bollen tegen elkaar aan, maar de lucht aan de binnenkant biedt een even grote tegendruk. Als gevolg merk je ook hier niets van de luchtdruk en kunnen we de halve bollen moeiteloos weer van elkaar afhalen. Maar dan pompen we de lucht aan de binnenkant weg met een vacuümpomp. Er ontstaat dan een zogenaamd vacuüm tussen de halve bollen. Als gevolg valt de tegendruk weg. De lucht drukt nu alleen nog vanaf buiten tegen de halve bollen (zie de rechter afbeelding). In dit geval krijgt zelfs de sterkste man op aarde de halve bollen niet uit elkaar getrokken!

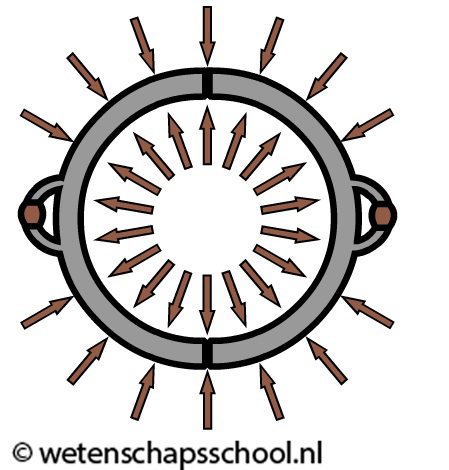
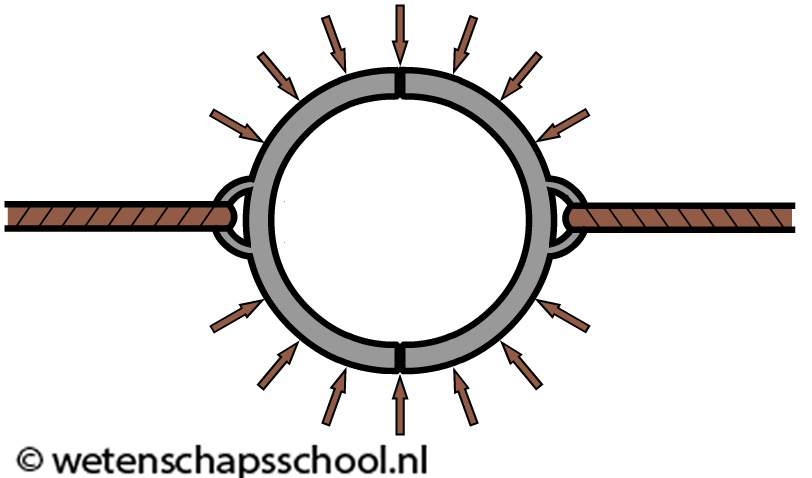
Sterker nog, in de 17^de eeuw is geprobeerd met zestien paarden de bollen uit elkaar te trekken, maar ook dit lukte niet!

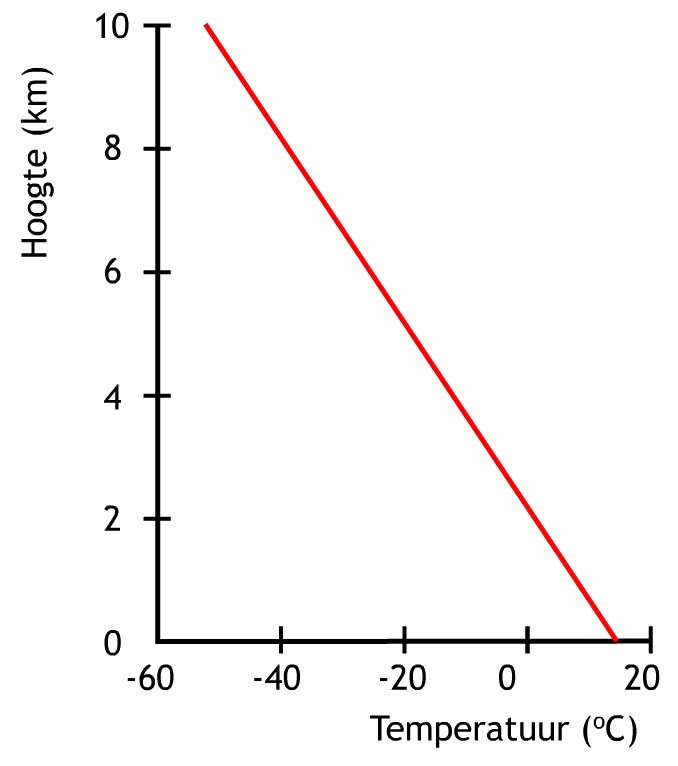
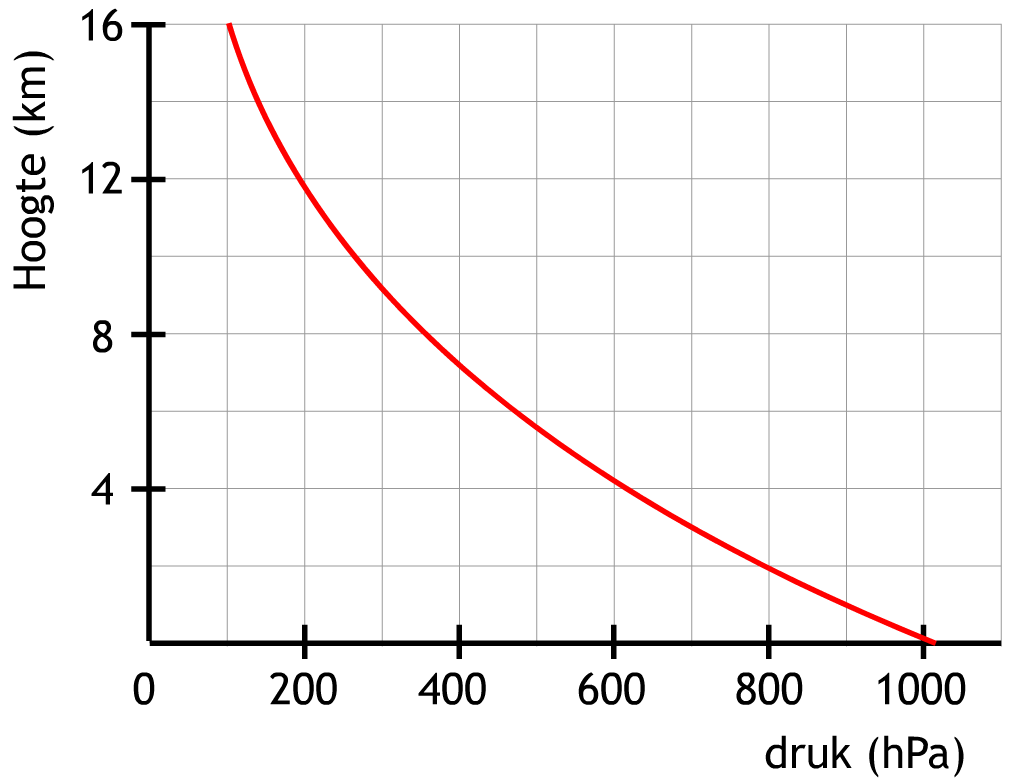
Laten we nu de atmosfeer nader bestuderen. De atmosfeer is een relatief dun laagje lucht dat door de zwaartekracht bij de aarde wordt gehouden. Ongeveer driekwart van de massa van de atmosfeer bevindt zich binnen 15 km van het aardoppervlak. Hoe hoger je in de atmosfeer komt, hoe minder lucht er boven je bevindt en hoe lager de luchtdruk dus wordt. In het onderstaande diagram kan je zien hoe de luchtdruk verandert met de hoogte. Je kan dit diagram ook vinden in BINAS. De grafiek wordt op een slimme manier gebruikt in bijvoorbeeld een vliegtuig. Door de luchtdruk buiten het vliegtuig te meten, kan je met deze grafiek de hoogte van het vliegtuig bepalen.

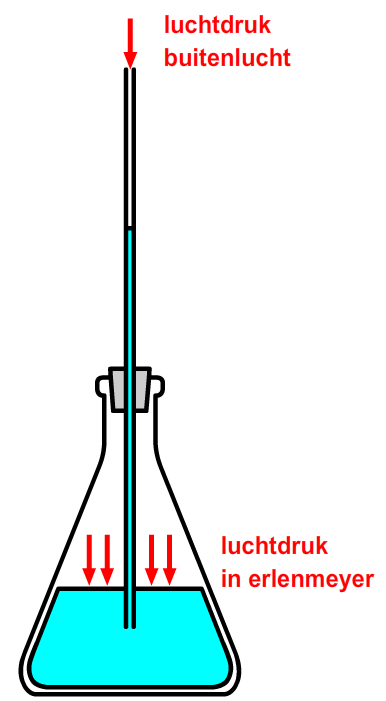
Het verschil in druk kan je al meten als je een paar verdiepingen omhoog of omlaag gaat in een gebouw. We kunnen dit zien met behulp van een simpele barometer (zie de onderstaande afbeelding). We zien hier een erlenmeyer met daarin een laag water. In de erlenmeyer zit een rubberen dop met een gat erin waarin je een dun buisje kan steken. Op deze manier is de lucht binnen de erlenmeyer niet meer in aanraking met de lucht buiten de erlenmeyer. Als je met deze fles een paar verdiepingen omhoog gaat, dan zal de buitenluchtdruk lager worden. Als gevolg duwt de grotere luchtdruk in de fles het water een klein stukje omhoog door het buisje. Bij elke 10 meter dat je stijgt zie je bij dit experiment een stijging van het water van ongeveer een centimeter.

(Afbeelding: Tace; PD-modified)

Leerdoelen:

Zorg dat je met het begrip druk en tegendruk kan beredeneren of je wel of niet iets merkt van de luchtdruk (bijvoorbeeld bij de Maagdenburger halve bollen)

Zorg dat je in BINAS het verband tussen druk en hoogte in de atmosfeer kan aflezen

Zorg dat je weet hoe een simpele barometer werkt. Water stijgt op in een buisje als de luchtdruk in de barometer groter is dan de buitenluchtdruk op een bepaalde hoogte

Opdrachten

(1p) Geef de luchtdruk op zeeniveau.

(1p) Bij welke hoogte is de luchtdruk nog maar de helft van deze waarde? Gebruik hiervoor het diagram uit de paragraaf.

(1p) De luchtdruk is gemiddeld 101 300 Pa. Deze druk voelen wij elk moment tegen ons lichaam drukken. Bereken hoeveel kracht de lucht op elke cm² van ons lichaam uitoefent.

(2p) Een half opgeblazen ballon bevindt zich in een afgesloten ruimte die vacuüm wordt gepompt. Leg met behulp van het begrip druk en tegendruk uit wat er met de ballon gebeurt.

(1p) Hieronder zien we hetzelfde flesje bij hoogte 4 km, 3 km en 300 m. Het flesje is tussen het nemen van de drie foto's niet open geweest. Verklaar wat er met het flesje is gebeurd.

(1p) Als je met de auto een berg oprijdt, kan je last krijgen van je oren. Dit komt door het verschil in luchtdruk binnen en buiten je oor. Leg uit aan welke kant de luchtdruk het hoogst is.

Heliumballonen worden gebruikt om metingen te doen hoog in de atmosfeer. Als je een heliumballon loslaat dan stijgt deze op. Tijdens het opstijgen zet de ballon flink uit.

(1p) Hoe komt het dat de ballon opstijgt?

(1p) Waarom zet de ballon uit bij het opstijgen?

Een ballon met een oppervlak van 0,015 m² wordt opgeblazen totdat de lucht in de ballon een druk van 1,3 bar uitoefent. 1 bar is gelijk aan 100.000 Pa.

(1p) Hoe kan je aan de ballon zien dat de luchtdruk aan de binnenzijde groter is.

(3p) Bereken de kracht die de lucht in de ballon uitoefent op de binnenwand van de ballon.

(2p) Als je drinkt met een rietje, dan wordt vaak gedacht dat je de vloeistof van je drankje "omhoog zuigt". In werkelijkheid duwt de buitenlucht de vloeistof door het rietje naar boven. Door je longen bij het zuigen groter te maken, maak je de luchtdruk in het rietje groter / kleiner. De luchtdruk buiten het rietje die op het drankje drukt is dan groter / kleiner dan de luchtdruk in het rietje. Hierdoor wordt de vloeistof in het rietje omhooggeduwd.

(2p) In de onderstaande afbeelding zien we een zogenaamd donderglas, bedacht door de Nederlander Gijsbrecht de Donckere in de 17^de eeuw. Als het water in de tuit snel stijgt, ging het volgens Gijsbrecht stormen. Leg aan de hand van dit resultaat uit of bij storm de luchtdruk hoger of lager wordt.

§3 Wolken (GEEN CE-STOF)

In deze paragraaf bespreken we de vorming van wolken.

Wolken bestaan uit kleine waterdruppels. Deze druppeltjes ontstaan als de waterdampmoleculen in de lucht aan elkaar beginnen te plakken. Als de temperatuur van de lucht te hoog is, dan bewegen de watermoleculen hier te snel voor, maar als de temperatuur onder het dauwpunt komt, dan lukt dit wel. We zien dit bijvoorbeeld bij de vorming van mist en wolken (zie de onderstaande afbeeldingen).

Bij hogere temperatuur kan de lucht dus meer waterdamp vasthouden zonder dat er druppels vormen. Koude lucht kan juist weinig waterdamp vasthouden en als gevolg vormen druppels hier al snel. Dit verklaart waarom mist en dauwdruppels vaak vormen in de ochtend, wanneer de lucht na de nacht flink is afgekoeld.

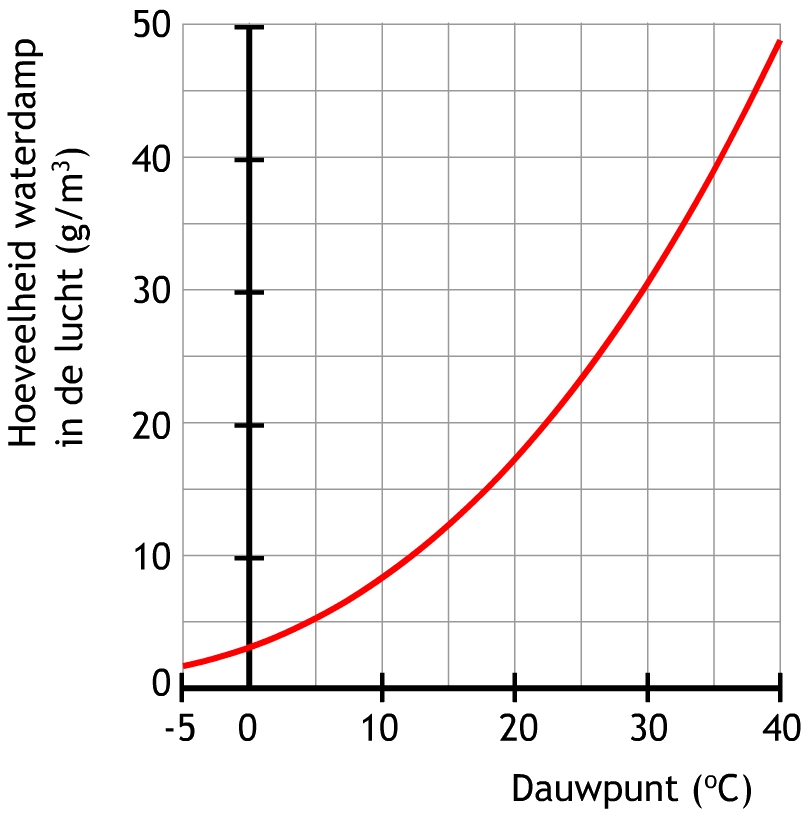
In het onderstaande diagram kan je zien hoeveel gram aan waterdamp een kubieke meter lucht kan vasthouden totdat het dauwpunt bereikt is. In het diagram lezen we bijvoorbeeld dat bij een temperatuur van 5 graden Celsius het dauwpunt al bereikt is als er iets meer dan 5 g/m³ waterdamp in de lucht zit. Bij 40 graden Celsius kan de lucht wel 48 g/m³ waterdamp vasthouden.

Het komt daarom geregeld voor dat er in een hete woestijn meer waterdamp in de lucht zit dan op een koude mistige winterdag in Nederland!

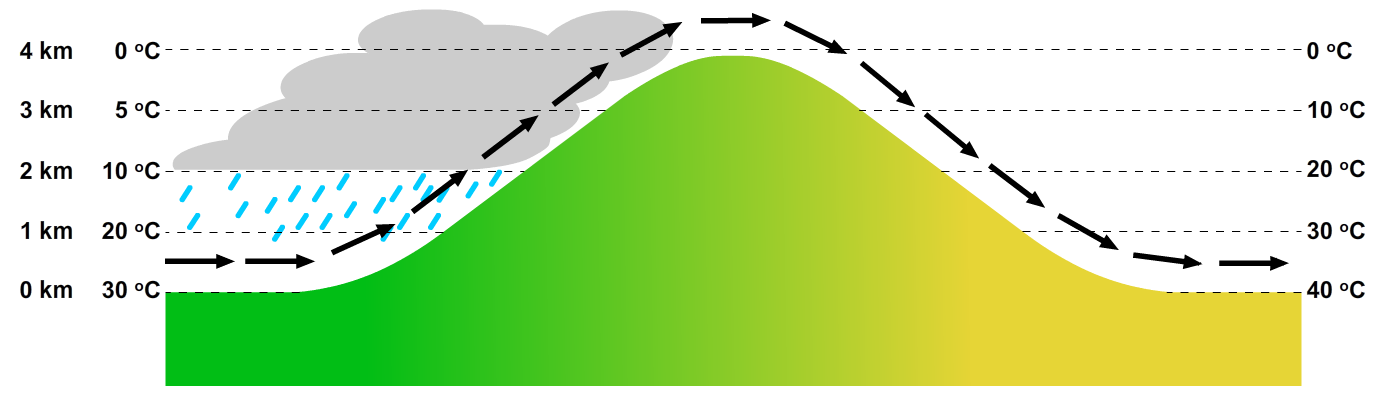
Het dauwpunt van lucht kan ook bereikt worden als lucht een paar kilometer omhoog verplaatst. Eerder in dit hoofdstuk hebben we gelezen dat de luchtdruk kleiner is op grotere hoogte. De kleinere druk zorgt ervoor dat de lucht uitzet en als gevolg neemt de temperatuur af. Als de temperatuur hierbij onder het dauwpunt komt, dan ontstaan wolken. De hoogte waarbij dit gebeurt noemen we het condensatieniveau. Maar hoe krijgen we lucht zo ver omhoog? Dit gebeurt bijvoorbeeld als lucht een berg opwaait (zie de onderstaande afbeelding). Dit verklaart waarom we vaak wolken rond bergtoppen zien.

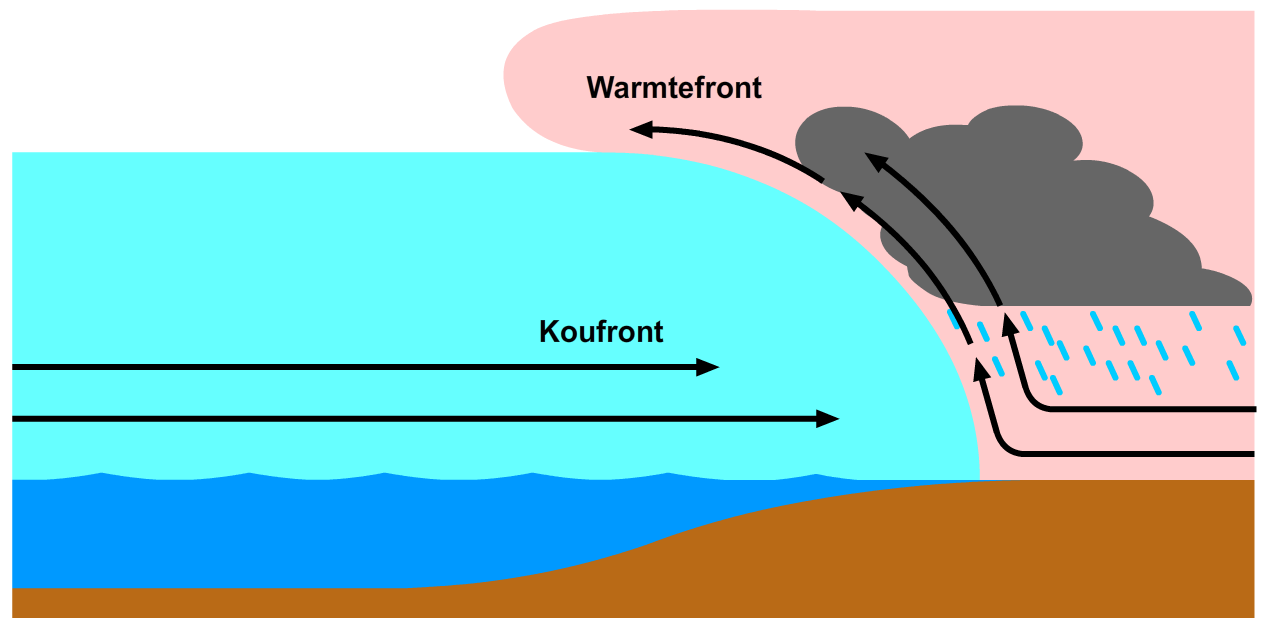
Nederland heeft dan wel geen bergen, maar wolken kunnen ook vormen als koude lucht richting warme lucht beweegt (zie de onderstaande afbeelding). De koudere lucht heeft een hogere dichtheid en als gevolg blijft het laag bij de grond. De warme lucht heeft een lage dichtheid en wordt door de koude lucht omhoog gedrukt. Bij het opstijgen koelt de warme lucht af. Als de temperatuur onder het dauwpunt komt, dan ontstaan er wolken.

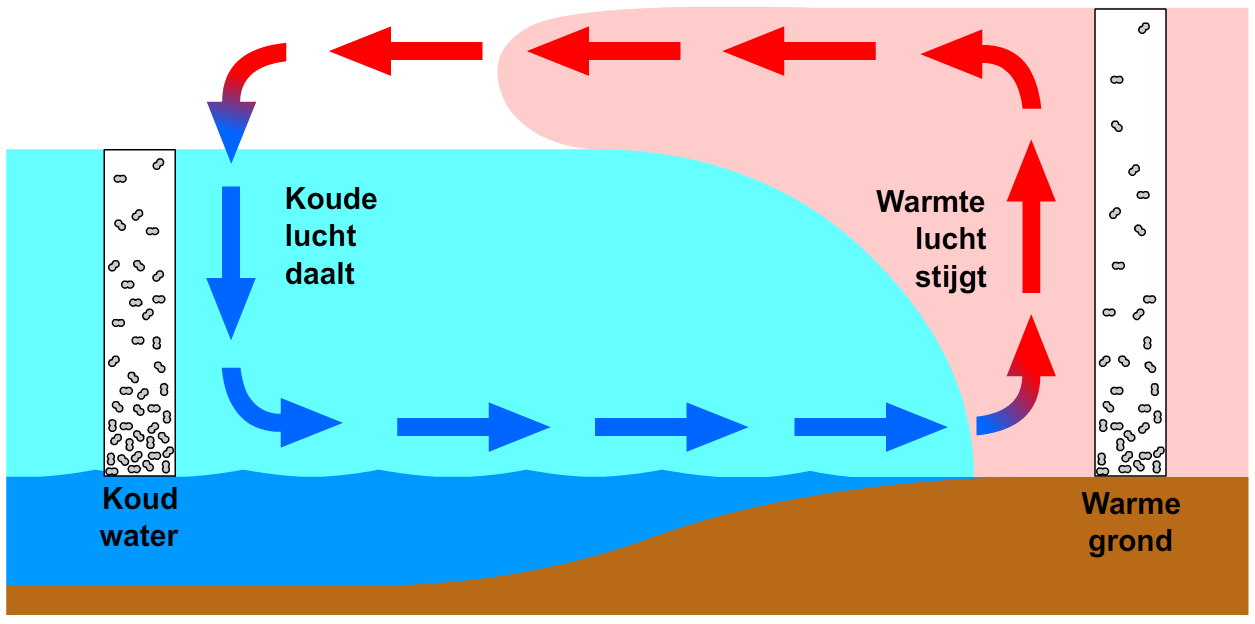
Dit proces is vaak zichtbaar aan de kust. Op een zonnige dag waait er aan de kust een wind vanaf de zee richting de kust. Dit noemen we ook wel de zeebries. De zeebries ontstaat doordat het land sneller opwarmt dan de zee als het wordt beschenen met zonlicht. Vervolgens maakt de warme grond de lucht erboven warm. De lucht boven het land zet daardoor uit en stijgt hierdoor op. Op grote hoogte is de druk in de rechter kolom nu groter dan de druk in de linker kolom. Hierdoor begint lucht naar links te waaien. Als gevolg hiervan ontstaat een circulaire stroming van lucht (zie de onderstaande afbeelding). In het hoofdstuk "Warmte" hebben we gezien dat ditzelfde proces ook optreedt als we lucht in een kamer verwarmen met een verwarming. We spraken toen van warmtestroming.

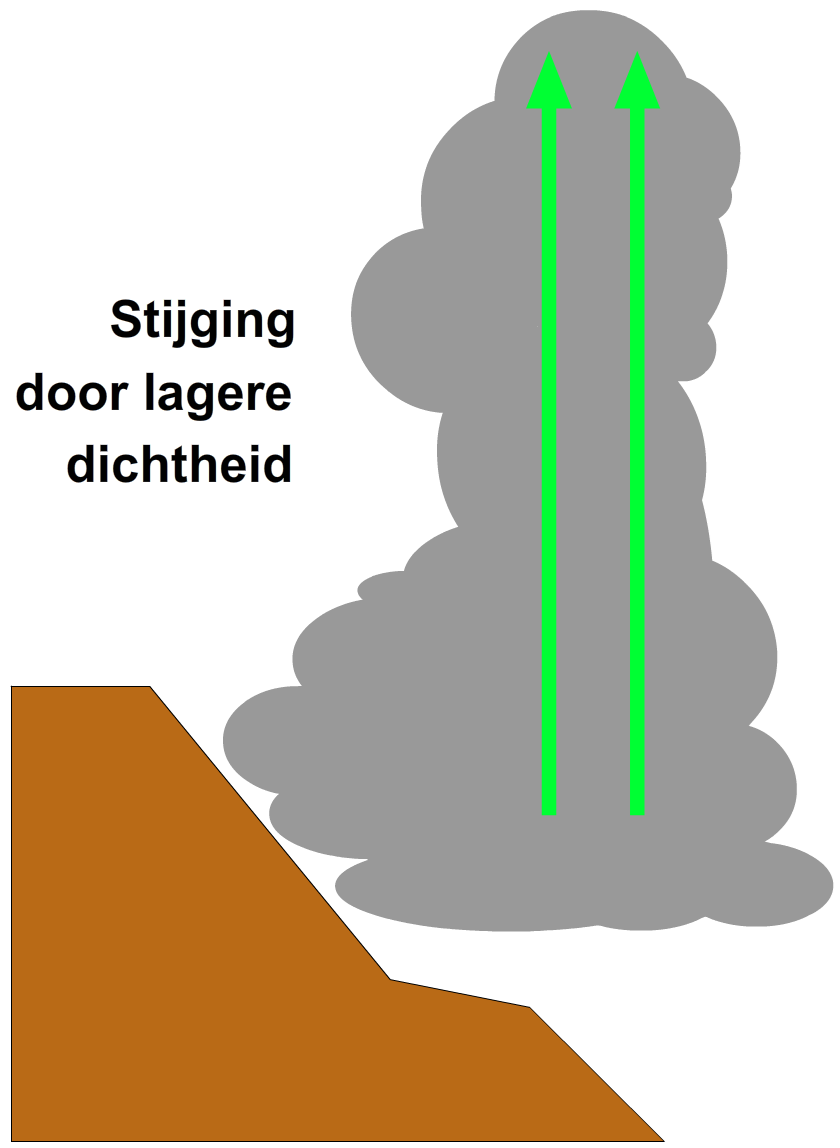
Als laatste bespreken we onweerswolken. Zoals je in de rechter afbeelding kan zien, zijn dit extreem dikke wolken. Deze wolken ontstaan als de dichtheid van de wolk kleiner is dan de dichtheid van de omliggende lucht. In dat geval gaat de wolk opstijgen. De wolk stopt met stijgen wanneer de dichtheid van de wolk gelijk wordt aan de dichtheid van de omgeving.

Leerdoelen:

Zorg dat je snapt dat waterdamp uit de lucht alleen kan condenseren tot druppels als de temperatuur laag genoeg is. Deze temperatuur noemen we het dauwpunt.

Zorg dat je aan de hand van de grafiek in de paragraaf kan aflezen dat koude lucht minder waterdamp kan vasthouden.

Zorg dat je weet dat wolken kunnen vormen als lucht met waterdamp omhoog wordt geduwd, bijvoorbeeld door een berg of een koude luchtstroom. Lucht koelt af als het opstijgt door de lagere druk en wolken ontstaan als de temperatuur onder het dauwpunt komt.

Zorg dat je de zeebries kan verklaren aan de hand van temperatuurverschillen tussen land en zee.

Zorg dat je met behulp van de dichtheid kan verklaren waarom onweerswolken vormen.

Opdrachten

Beantwoord de volgende vragen met het diagram uit de paragraaf.

(1p) Vormen wolken bij een temperatuur van 10 graden Celsius met 15 gram waterdamp per kubieke meter lucht? Leg je antwoord uit.

(1p) Op een warme dag is de buitentemperatuur 30 graden Celsius. Er zit 20 gram waterdamp per kubieke meter in de lucht. Leg uit of er mist vormt.

(1p) De temperatuur koelt dan plots een stuk af. Bij welke temperatuur kan mist zichtbaar worden? Leg je antwoord uit

(2p) In een woestijn met een temperatuur van 40 ^oC en in Nederland met een temperatuur van 15 ^oC zit 25 gram waterdamp per kubieke meter in de lucht. Leg uit in welke situatie mist te zien is en in welke niet.

(1p) Leg uit waarom wolken vaak ontstaan als lucht een berg op geblazen wordt.

(2p) Een hoeveelheid stijgende lucht bevat 3 gram waterdamp per kubieke meter op het moment dat wolken vormen. In het onderstaande diagram is de temperatuur van de atmosfeer te zien bij verschillende hoogten. Leg hiermee uit op welke hoogte het condensatieniveau zich bevindt.

(1p) Is de zeebries een vorm van warmtegeleiding, warmtestroming of warmtestraling?

(1p) Een onweerswolk vormt wanneer de dichtheid van een wolk groter / kleiner is dan de dichtheid van de lucht in de omgeving van de wolk.

BINAS:
7-12	Formules
26	Luchtdruk en hoogte

Hoofdstuk 7 Het weer

§1 De druk

§2 De luchtdruk (GEEN CE-STOF)

§3 Wolken (GEEN CE-STOF)

Hoofdstuk 7
Het weer