Hoofdstuk 5
Elektriciteit I
§1 Schakelingen §2 De stroomsterkte §3 De spanning §4 De wet van Ohm §5 Vervangingsweerstand §6 Het vermogen
§1 Schakelingen
In dit hoofdstuk gaan we elektriciteit bestuderen. Omdat elektriciteit wordt veroorzaakt door bewegende ladingen, gaan we in de eerste paragraaf lading bestuderen.
Alle materie in het universum bestaat uit bolvormige deeltjes die we atomen noemen. Atomen bestaan op hun beurt uit nog kleinere deeltjes. In de atoomkern bevinden zich deeltjes met een positieve lading. Deze deeltjes zijn relatief zwaar en zitten stevig vast in de atoomkern. Om de atoomkern heen bewegen een aantal deeltjes met een negatieve lading. Deze deeltjes zijn relatief licht en bewegen met enorme snelheid om de atoomkern. Het zijn deze negatieve ladingen die zorgen voor elektriciteit.
De positieve en de negatieve ladingen hebben de bijzondere eigenschap dat ze elkaar aantrekken met behulp van de elektrische kracht. Daarnaast is het zo dat ladingen van dezelfde soort elkaar afstoten met dezelfde elektrische kracht.
Demonstratievideo
| ||
|
Als we elektriciteit willen opwekken, dan hebben we in ieder geval een spanningsbron nodig. Een spanningsbron bevat twee polen met een verschillende hoeveelheid lading. In het geval van een batterij is de ene pool negatief geladen (de zogenaamde minpool), en is de andere pool positief geladen (de zogenaamde pluspool).
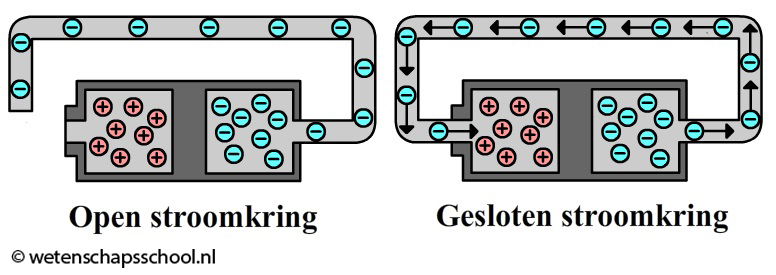
Als de twee polen niet verbonden zijn, dan spreken we van een open stroomkring en gaat er geen elektriciteit stromen. Als we de twee polen wel verbinden, dan spreken we van een gesloten stroomkring (zie de volgende afbeelding). Als gevolg gaan de negatieve ladingen naar de pluspool stromen. Het bewegen van deze ladingen noemen we elektriciteit.
Er bestaan twee soorten spanningsbronnen: gelijkspanning en wisselspanning. Een batterij werkt bijvoorbeeld op gelijkspanning. Over de voedingskasten bij de natuurkundeles staat ook gelijkspanning. Bij deze spanningsbronnen loopt de stroom in één richting van de plus naar de min. Over het stopcontact staat echter wisselspanning. Hier draait de stroomrichting 50 keer per seconde om. Het symbool hiervoor is hieronder afgebeeld. In een later hoofdstuk ga je hier meer over leren.
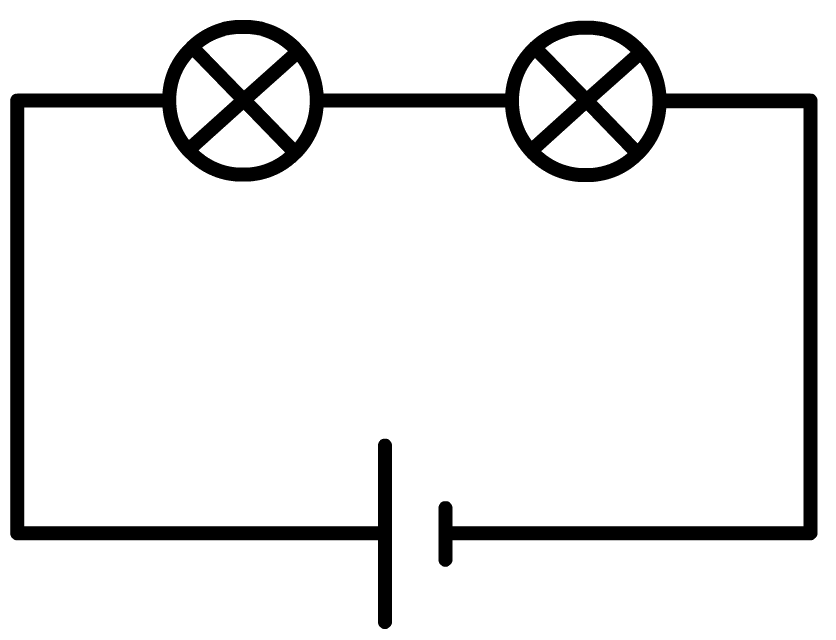
In de onderstaande afbeelding is aan de stroomkring ook een gloeilamp en een schakelaar toegevoegd. Een schakelaar is niet meer dan een klepje, waarmee de stroomkring geopend en gesloten kan worden. Alleen als de schakelaar gesloten is gaan de ladingen van de min- naar de pluspool stromen.
Als de ladingen door de schakeling stromen, dan botsen ze voortdurend tegen de atomen waaruit de schakeling bestaat. In de gloeidraad van een gloeilamp leveren deze botsingen genoeg energie om de draad zo warm te maken dat deze gaat gloeien.
Aan de rechterkant zien we ook een schematische weergave van deze schakeling. Zoals je ziet gebruiken we voor de lamp een cirkel met een kruis erin en voor de spanningsbron een korte en een lange streep (de lange streep is de pluspool). Deze en vele andere symbolen voor elektrische onderdelen kan je in BINAS vinden.
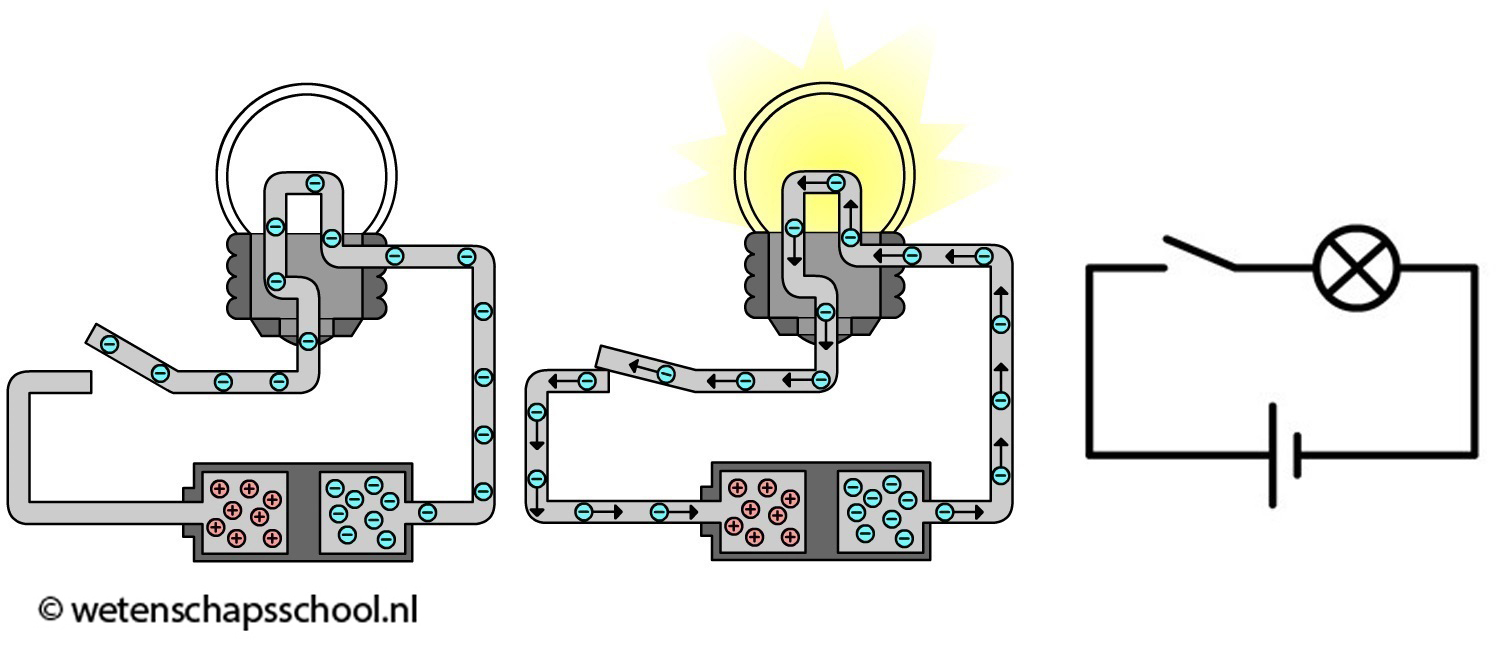
Het zijn alleen de negatieve elektronen die door de elektriciteitsdraden stromen van de min naar de plus. De positieve ladingen zitten immers goed vast in de atoomkernen. Toch zeggen we (helaas) dat de stroom van plus naar min stroomt, terwijl dus in werkelijkheid de elektronen precies de andere kant op bewegen! Deze onhandigheid stamt nog uit de tijd voordat elektronen ontdekt waren.
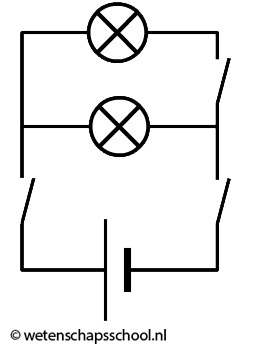
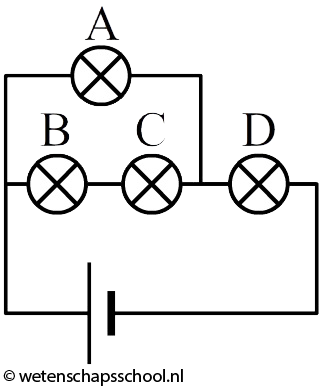
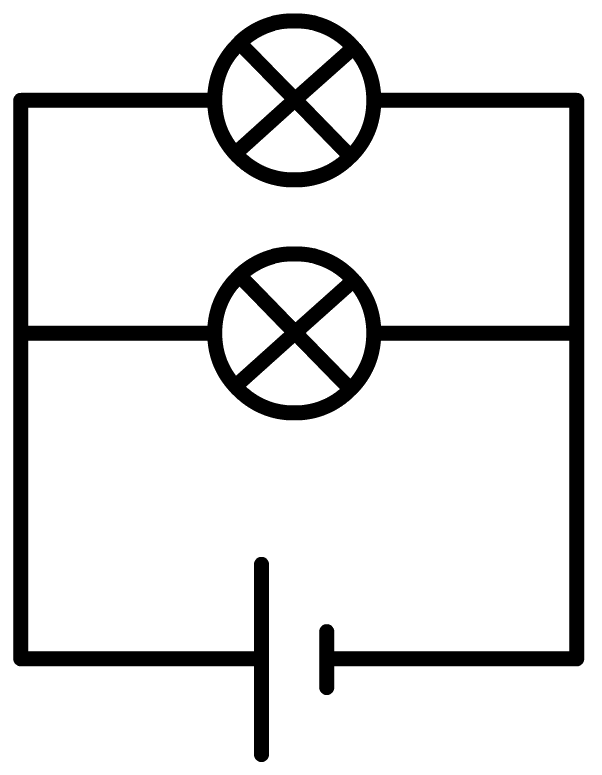
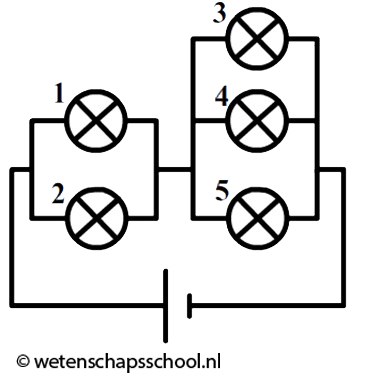
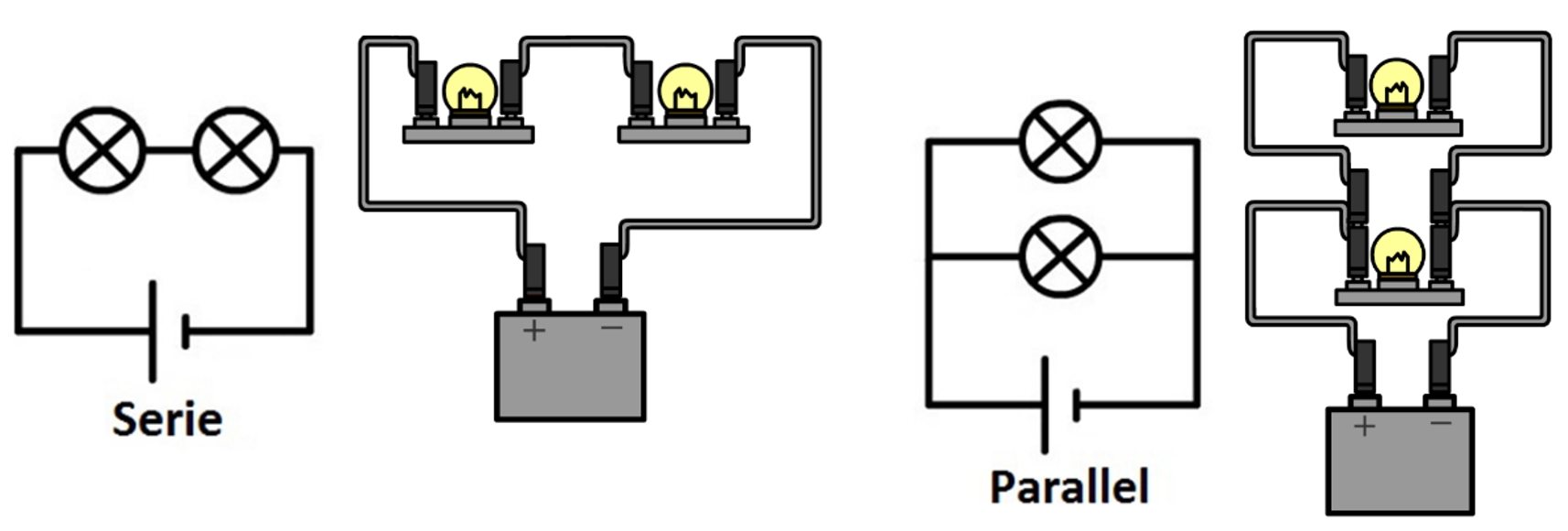
Als we meerdere lampjes op een spanningsbron aansluiten, dan kunnen we dat op verschillende manieren doen. Linksonder zien we de zogenaamde serieschakeling. In een serieschakeling zijn alle lampjes in dezelfde stroomkring opgenomen. Als we in deze schakeling één lampje losdraaien, dan wordt deze stroomkring verbroken en gaan alle lampjes uit. Rechts zien we de zogenaamde parallelschakeling. In een parallelschakeling heeft elk lampje zijn eigen stroomkring. Als we in deze schakeling één lampje losdraaien, dan wordt slechts één van de stroomkringen verbroken. De andere lampjes blijven in dat geval gewoon branden.
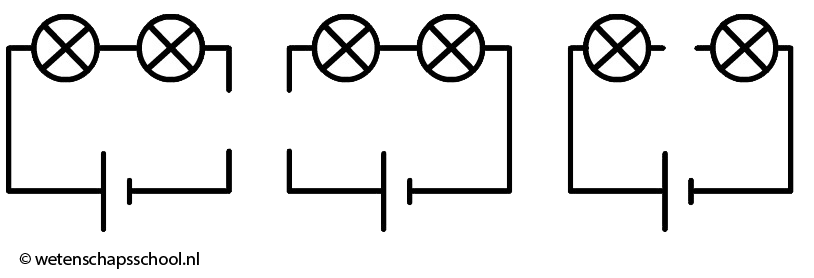
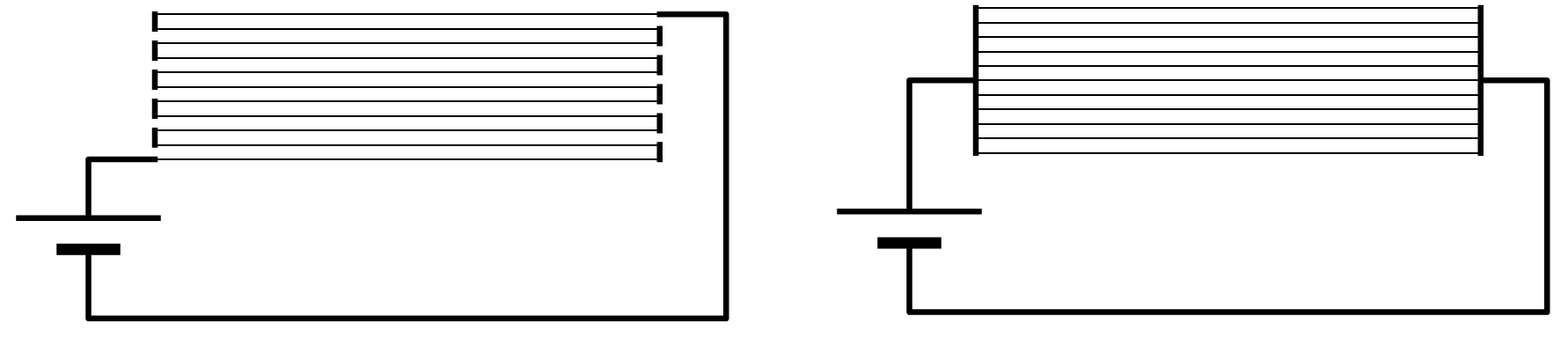
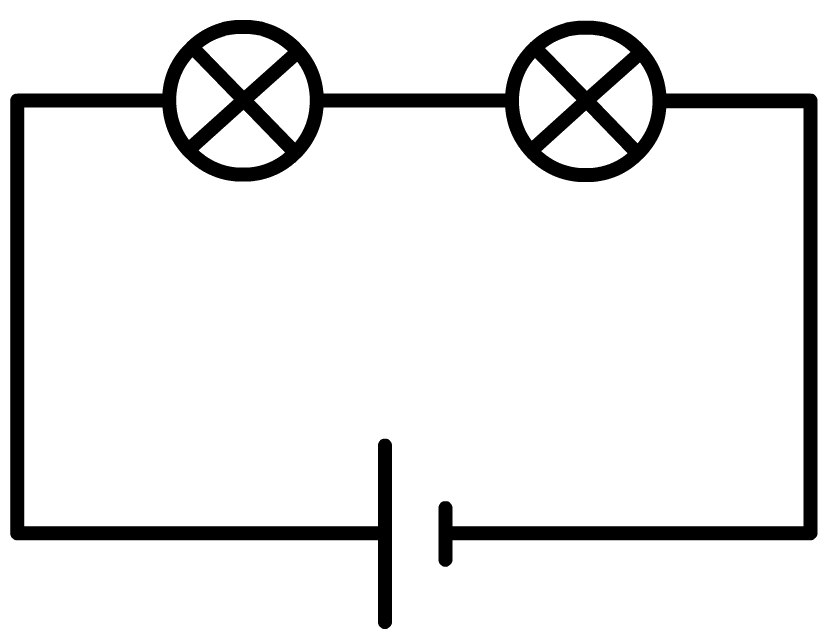
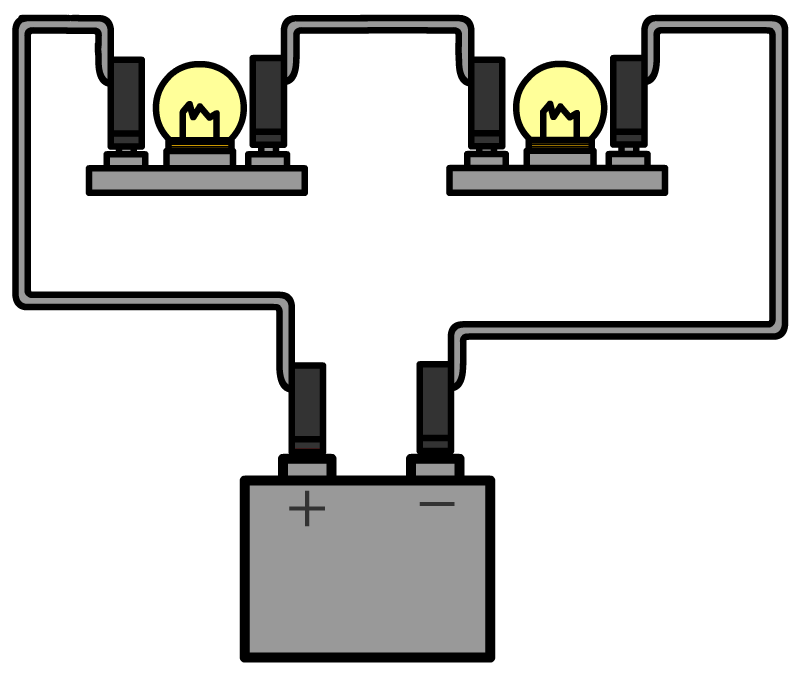
Linksonder zien we wederom een serieschakeling met twee lampjes. Rechts is dezelfde schakeling weergegeven, maar nu is één draadje uit de spanningsbron losgemaakt. Zoals je ziet is er nu geen gesloten stroomkring meer en als gevolg gaan beide lampjes uit.
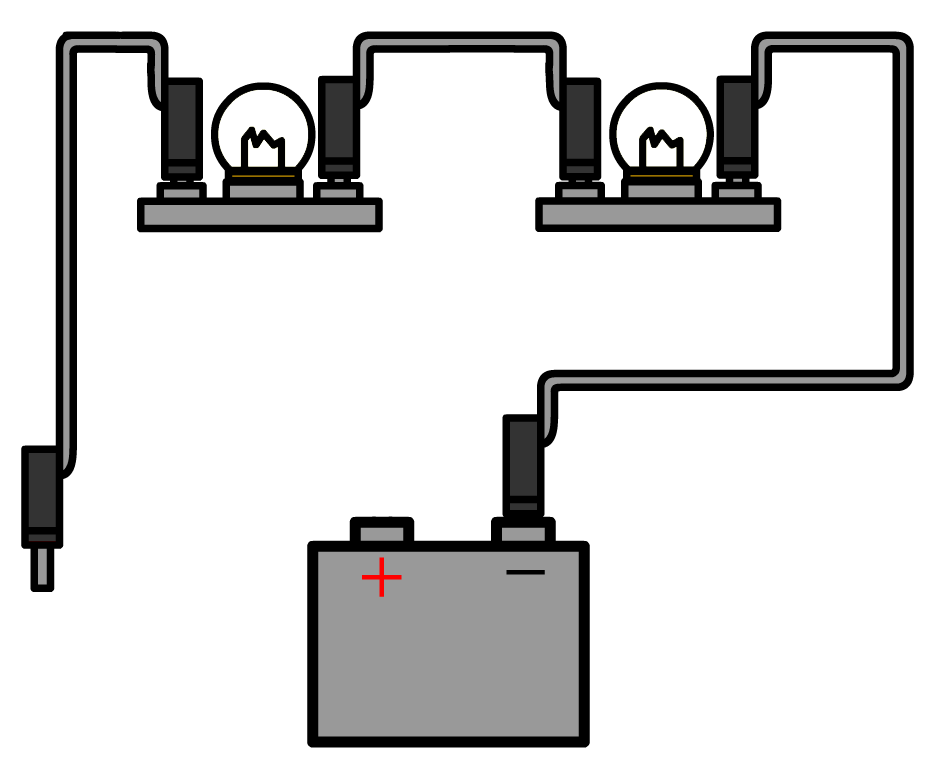
Hieronder halen we één draad uit de spanningsbron van een parallelschakeling. Als gevolg worden beide stroomkringen verbroken en gaan ook hier beide lampjes uit.
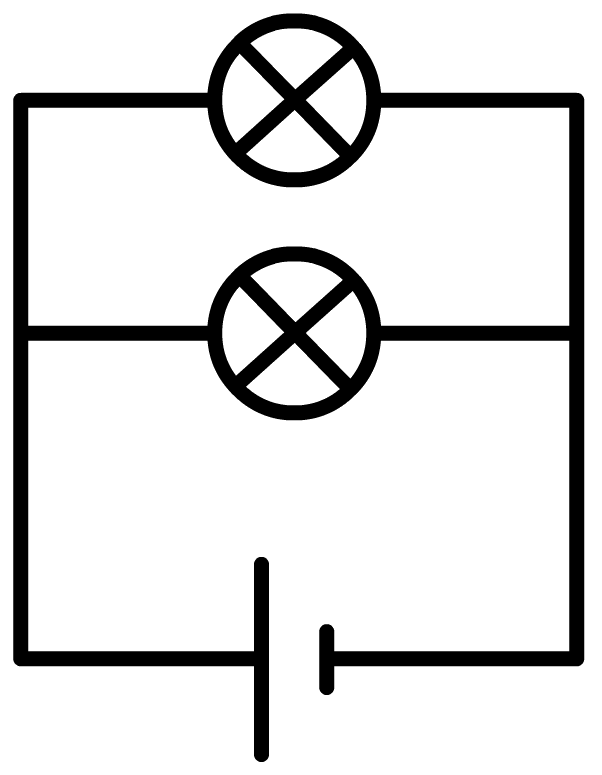
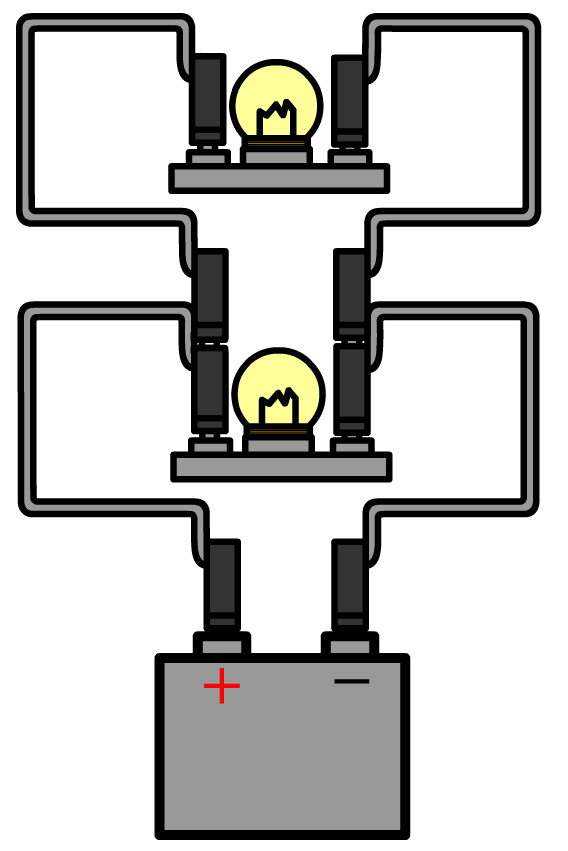
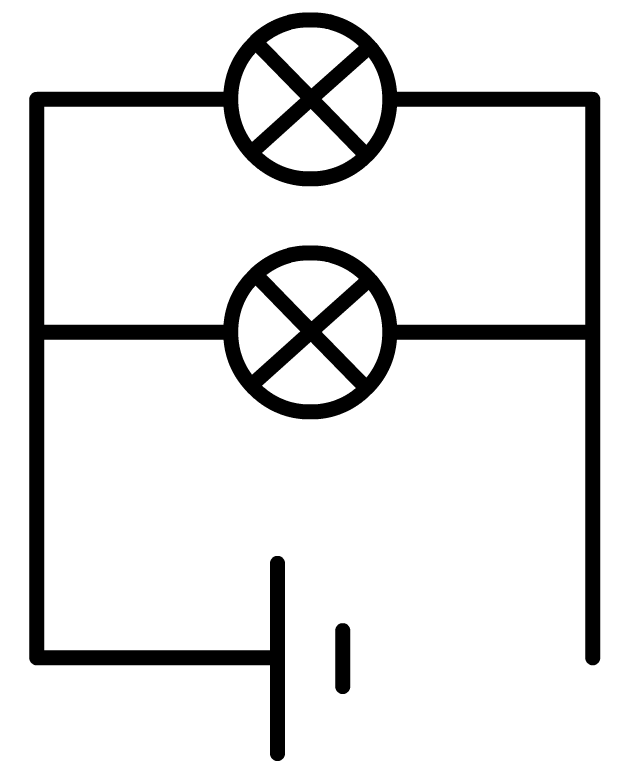
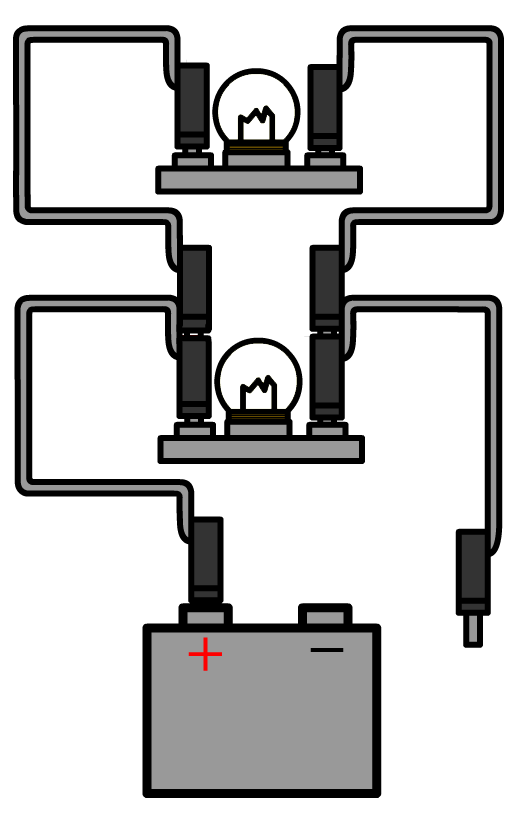
Nu halen we bij de parallelschakeling de draden uit één kant van het onderste lampje. Nu is de stroomkring door het onderste lampje verbroken, maar de stroomkring door het bovenste lampje is nog in tact. Als gevolg blijft het bovenste lampje branden.
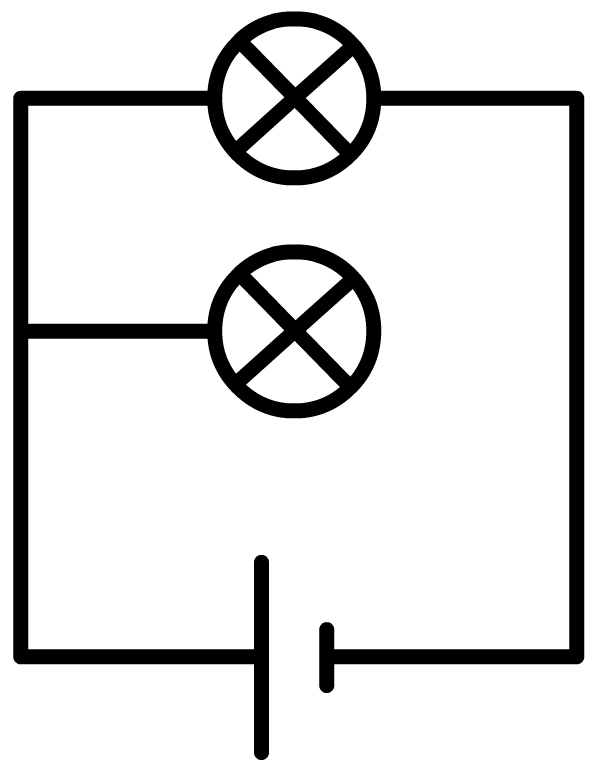
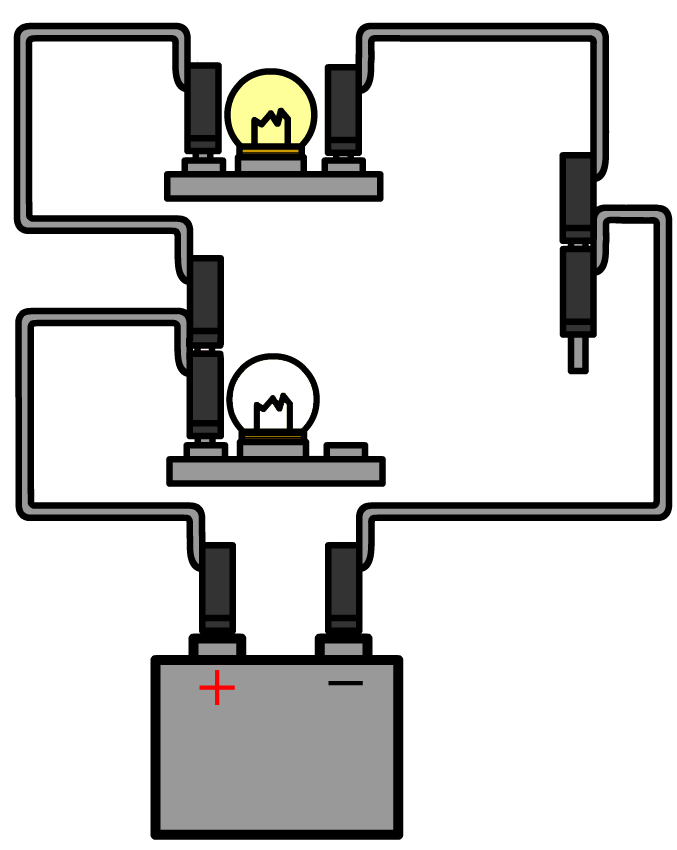
We eindigen deze paragraaf met het begrip weerstand. De weerstand vertelt ons hoe moeilijk het is voor ladingen om door een materiaal te stromen. Materialen met een kleine weerstand noemen we geleiders. De bekendste groep geleiders zijn de metalen. We gebruiken geleiders bijvoorbeeld voor de bedrading in schakelingen, zodat ladingen hier gemakkelijk doorheen stromen. Meestal wordt hier koper gebruikt. Materialen met een grote weerstand noemen we isolatoren. Een veelvoorkomende isolator is kunststof. Elektriciteitsdraden zijn meestal omhult met een laagje kunststof. Dit zorgt er o.a. voor dat er geen kortsluiting kan ontstaan tussen verschillende draden (of dat er geen stroom door je lichaam gaat lopen als je de draden vastpakt).
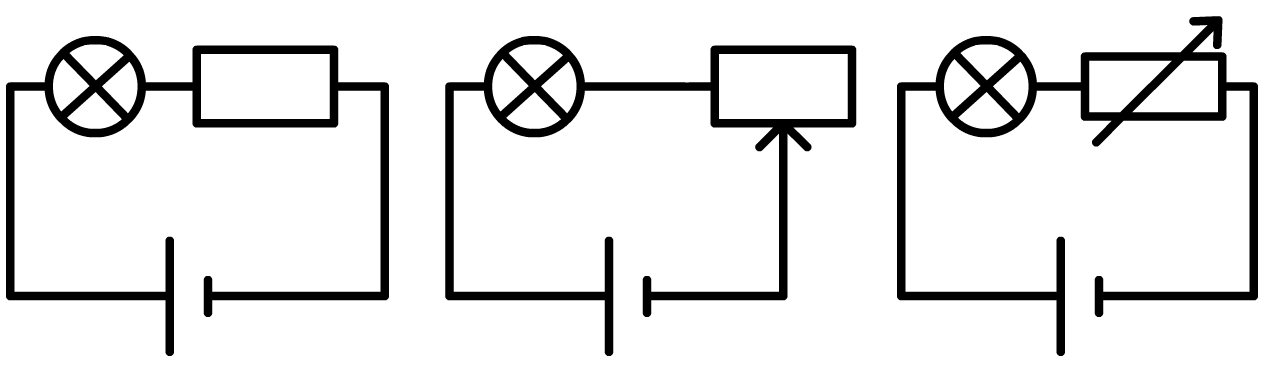
Naast het begrip "weerstand" is er ook een elektrisch component met de naam weerstand. Het rechthoekige symbool in de eerste onderstaande afbeelding wordt een (vaste) weerstand genoemd. Een weerstand wordt o.a. gebruikt om de stroom door een draad te beperken. Als je een zwak lampje bijvoorbeeld direct op een stopcontact aansluit, dan brandt het meteen door. Dit is te verhelpen door een weerstand in serie te zetten met de lamp.
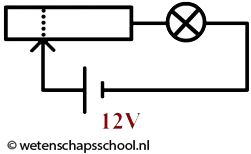
Naast een vaste weerstand bestaat ook de zogenaamde variabele weerstand. De rechter twee schakelingen bevatten twee symbolen die hier vaak voor gebruikt worden. De waarde van deze weerstand is handmatig in te stellen met een schuif- of een draaiknop (zie de rechter afbeelding). Dit onderdeel wordt bijvoorbeeld gebruikt om een lamp handmatig te dimmen.
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
INSTRUCTIE:
Elektriciteit
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§2 De stroomsterkte
In deze paragraaf gaan we de beweging van lading nader bestuderen. Dit doen we aan de hand van het begrip stroomsterkte.
De hoeveelheid lading die per seconde door een punt in de schakeling stroomt noemen we de stroomsterkte (I). De SI-eenheid van de stroomsterkte is de ampère (A).
Laten we eens kijken hoe het zit met de stroomsterkte in een aantal verschillende schakelingen. In de onderstaande animatie stromen ladingen door een serieschakeling. Een serieschakeling bestaat slechts uit één stroomkring. Als gevolg gaan alle ladingen die uit de spanningsbron stromen door alle lampjes heen. De hoeveelheid ladingen die uit de spanningsbron stromen, is dus gelijk aan de hoeveelheid ladingen die het rechter lampje in stromen en even later het linker lampje in stromen. De stroomsterkte is in een serieschakeling dus in alle onderdelen gelijk.
Hieronder zien we een parallelschakeling. In dit geval zijn er meerdere stroomkringen waarover de lading zich verdeelt. Hoe de stroomsterkte zich verdeelt, hangt af van de weerstand van de lampjes. Alleen als de lampjes dezelfde weerstand hebben, zal de stroomsterkte zich gelijk verdelen over de lampjes.
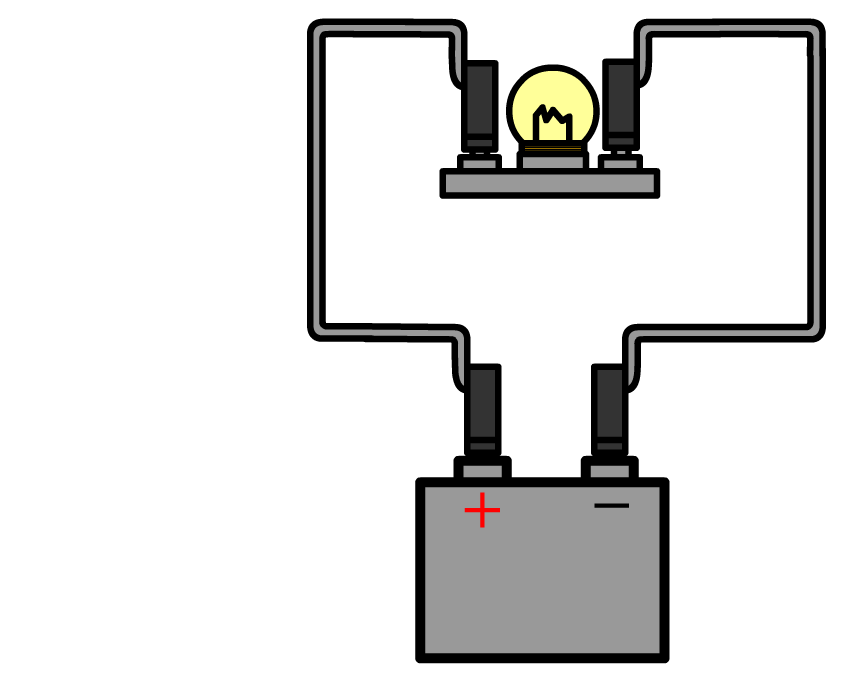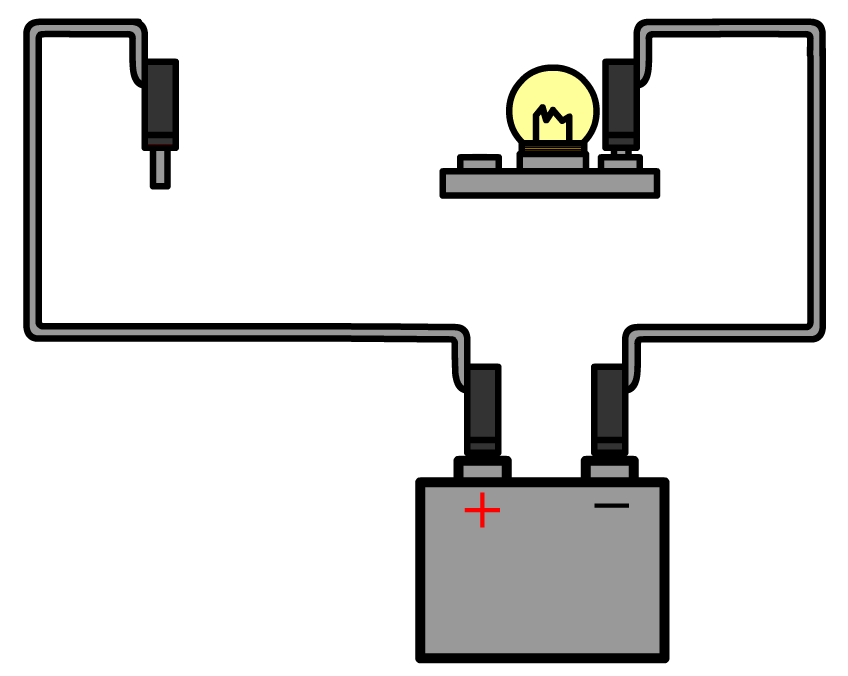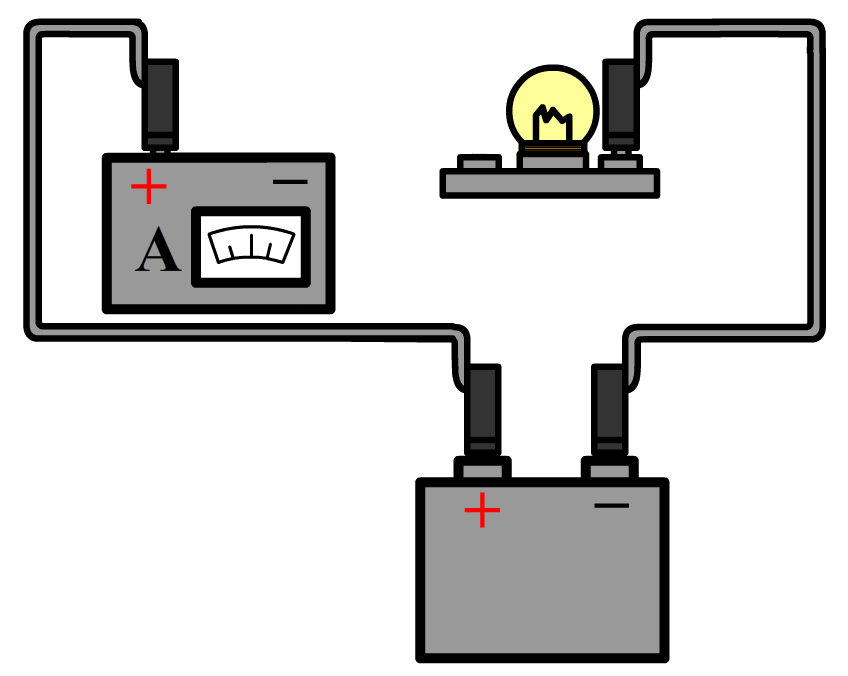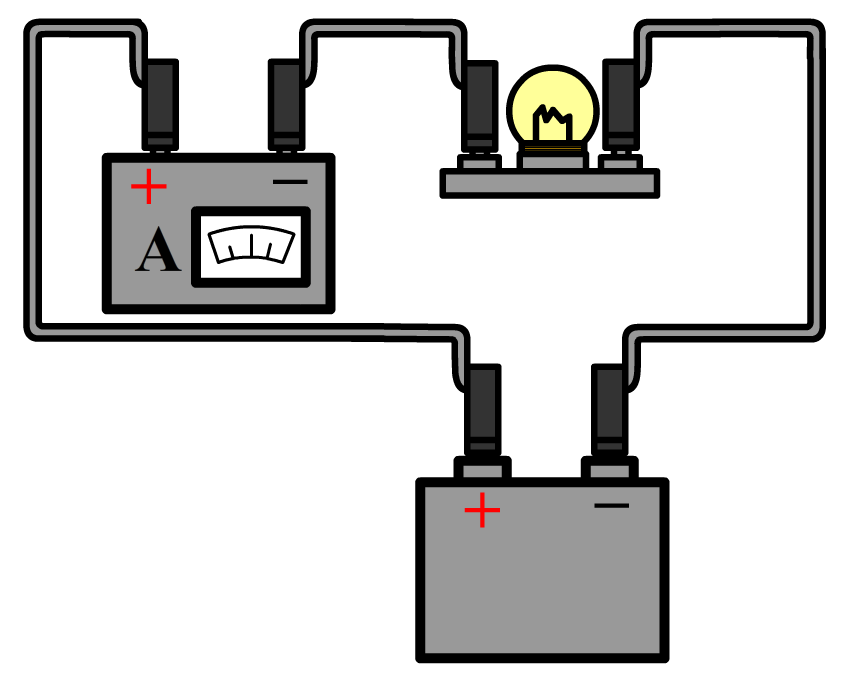
De stroomsterkte kunnen we meten met een zogenaamde ampèremeter (ook wel stroommeter genoemd). De ampèremeter sluit je in serie aan naast het onderdeel waarvan je de stroomsterkte wilt meten. Hieronder zie je in stappen hoe je de stroomsterkte meet door bijvoorbeeld een lamp. Haal één van de draden los uit de lamp en sluit de ampèremeter dan hiertussen aan. Zorg dat de pluskant van de stroommeter aangesloten wordt aan de pluskant van de stroomkring. Als je dit verkeerd om doet, dan werken de meeste stroommeters niet. Rechts zien we ook een schematische versie van de schakeling. Zoals je ziet tekenen we een ampéremeter als een rondje met de letter "A" erin.
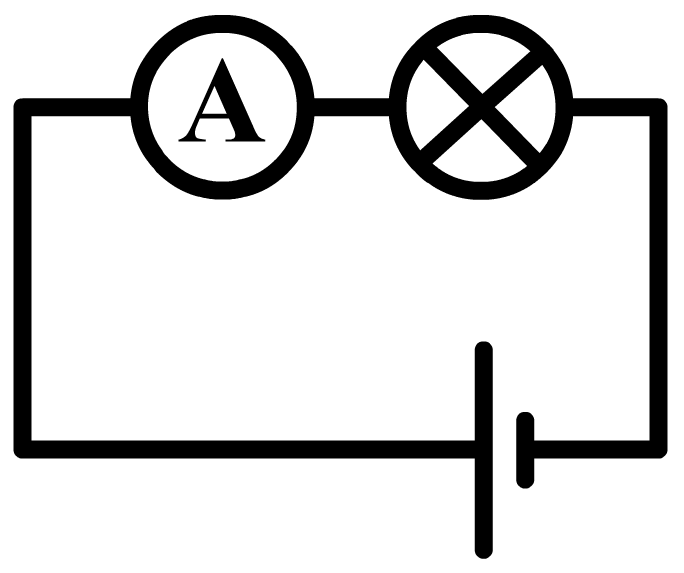
We kunnen dit ook doen in een serieschakeling. Hier wordt de stroomsterkte gemeten door het linker lampje:
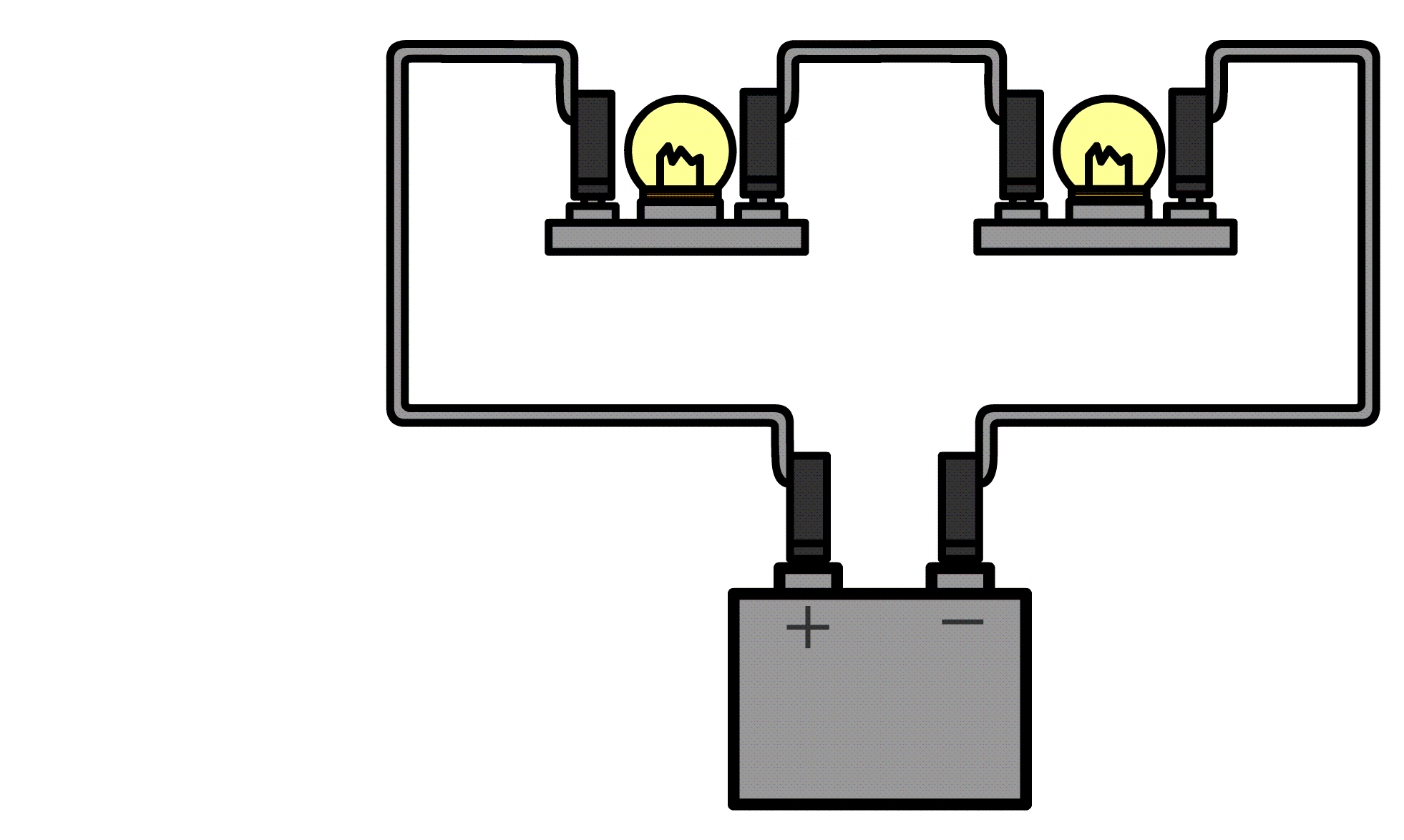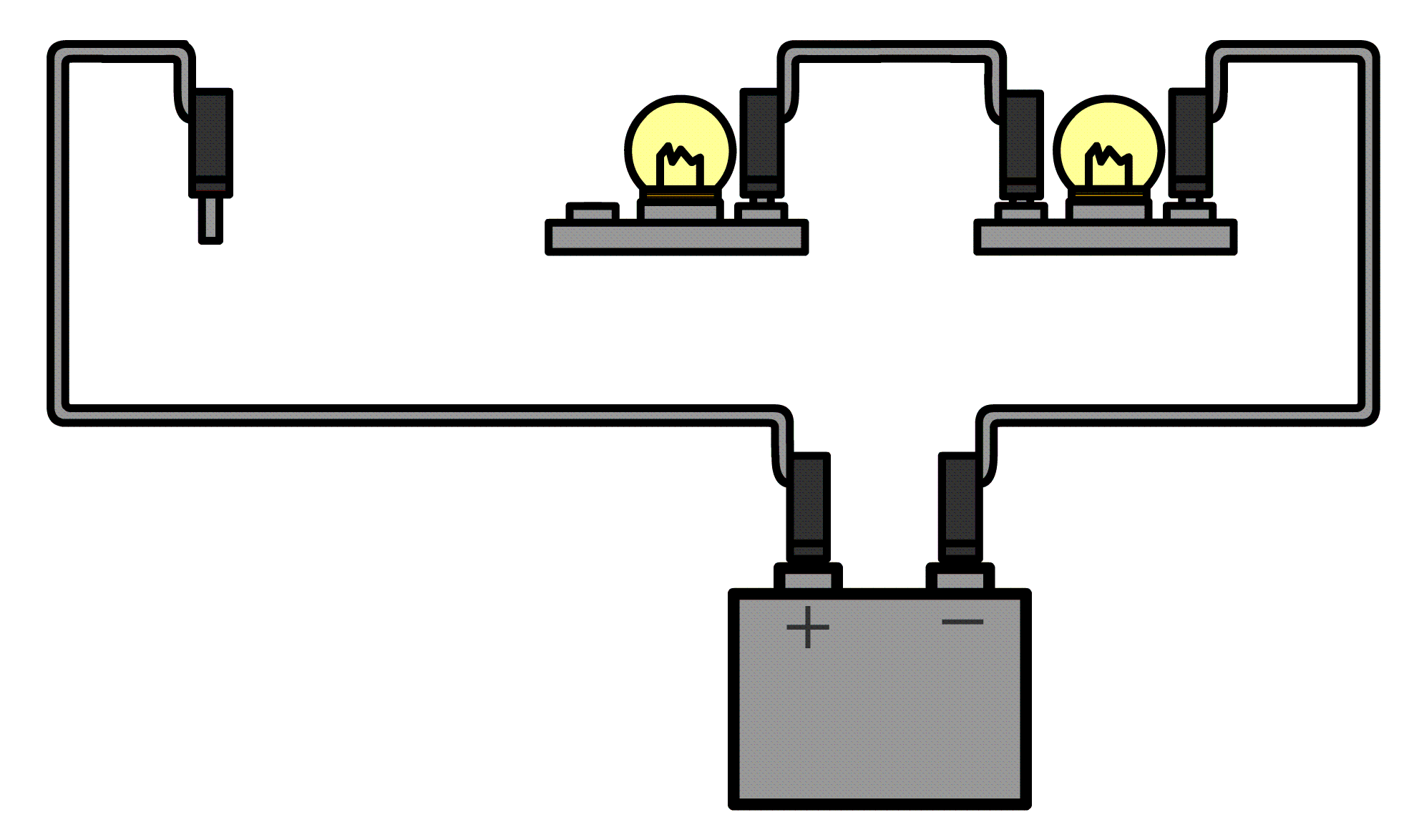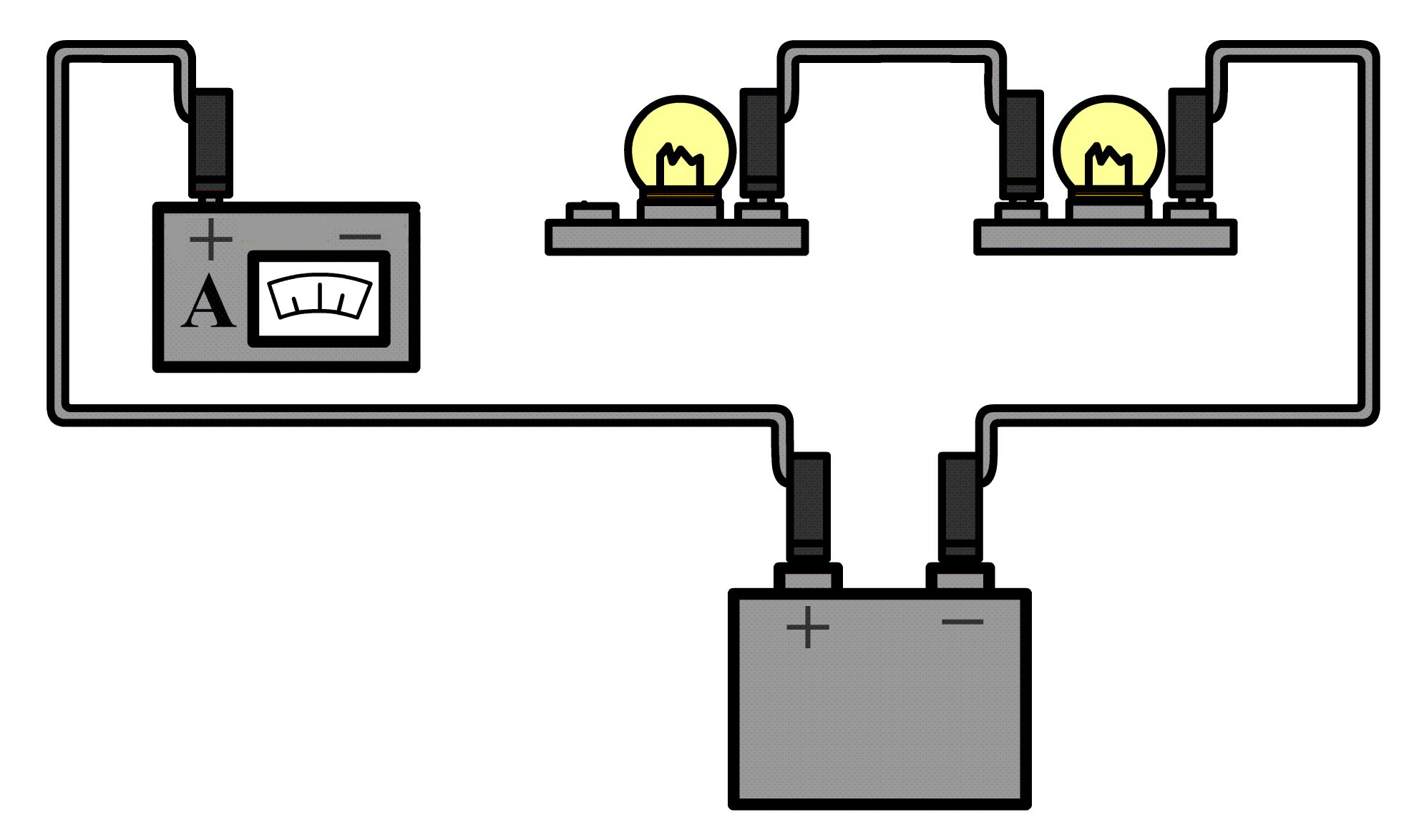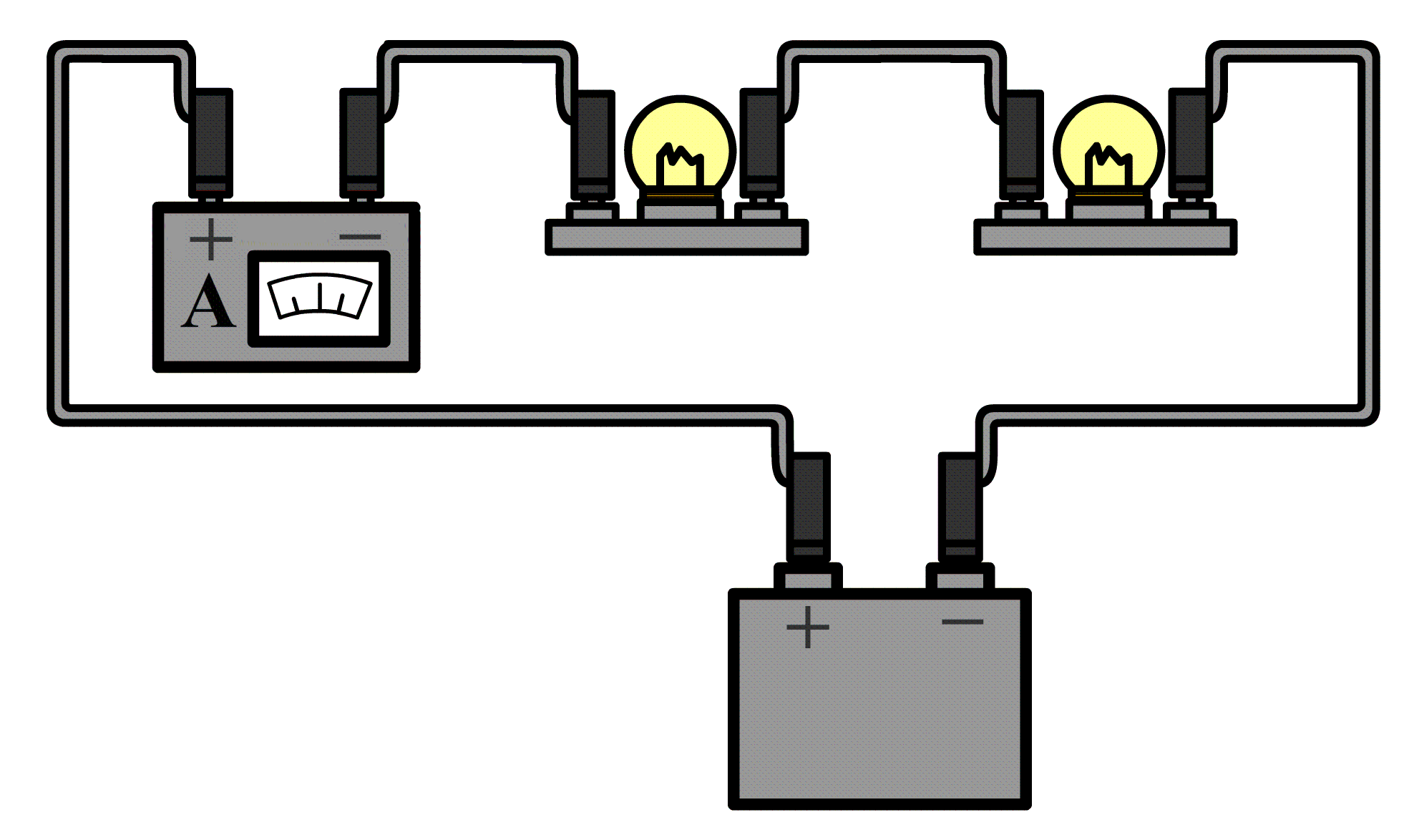
Hieronder doen we hetzelfde voor de spanningsbron. Haal één van de draden los uit de spanningsbron en sluit de ampèremeter dan hiertussen aan.
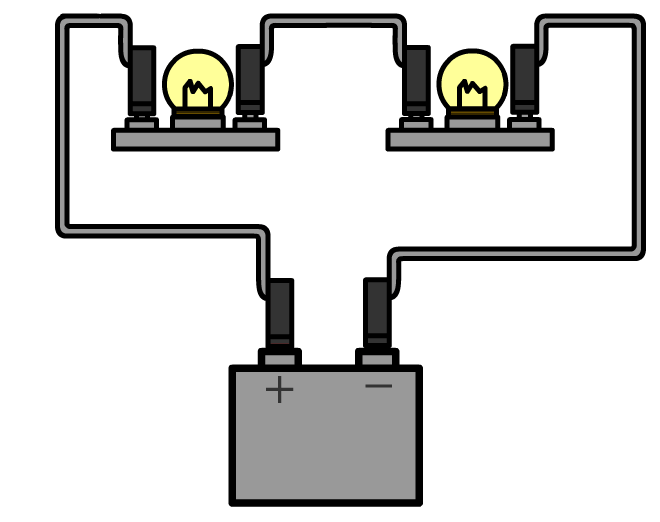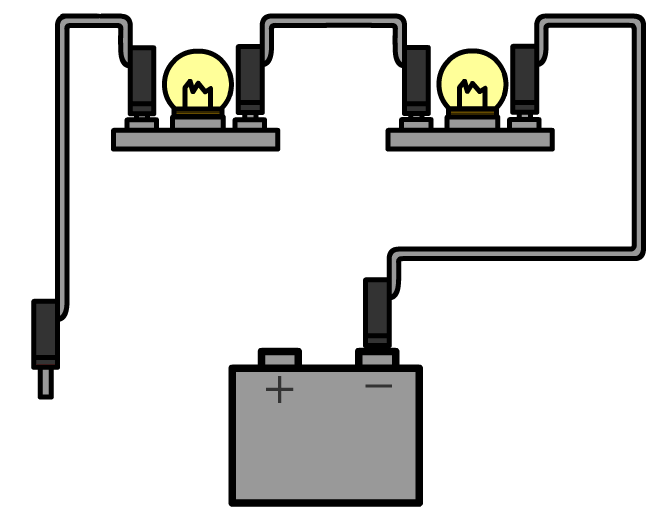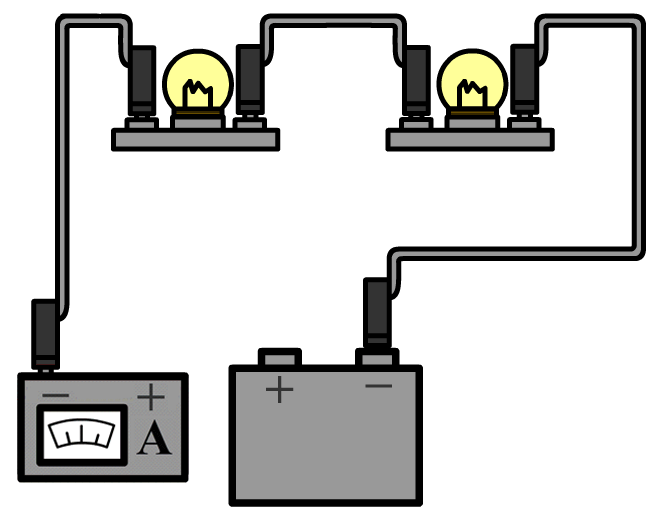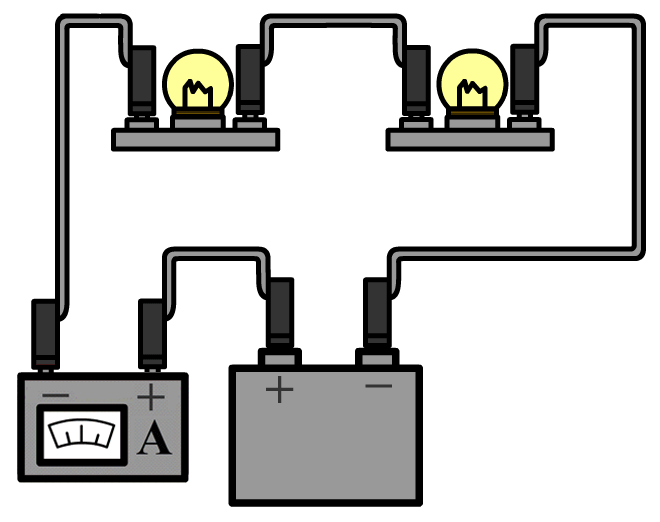
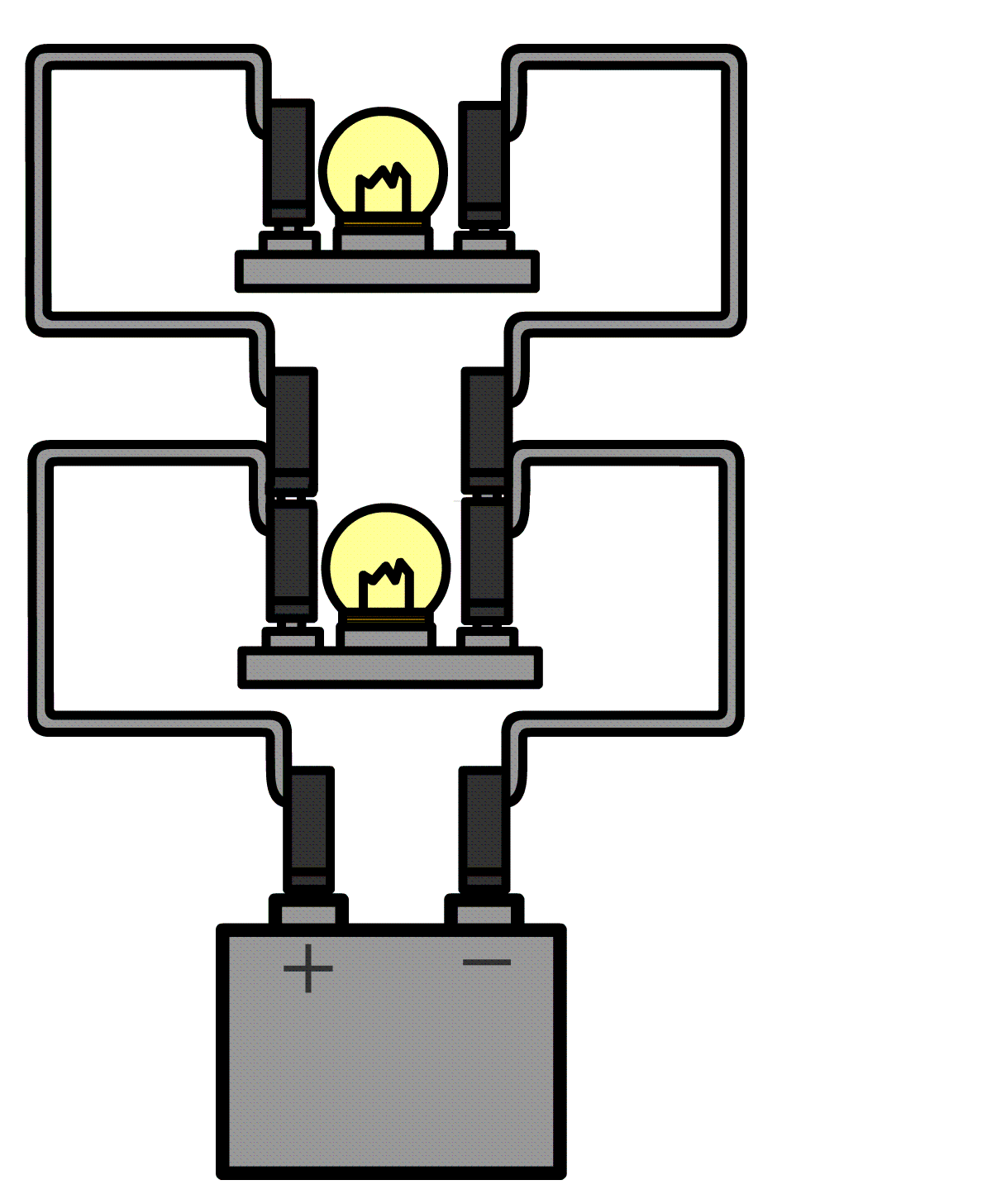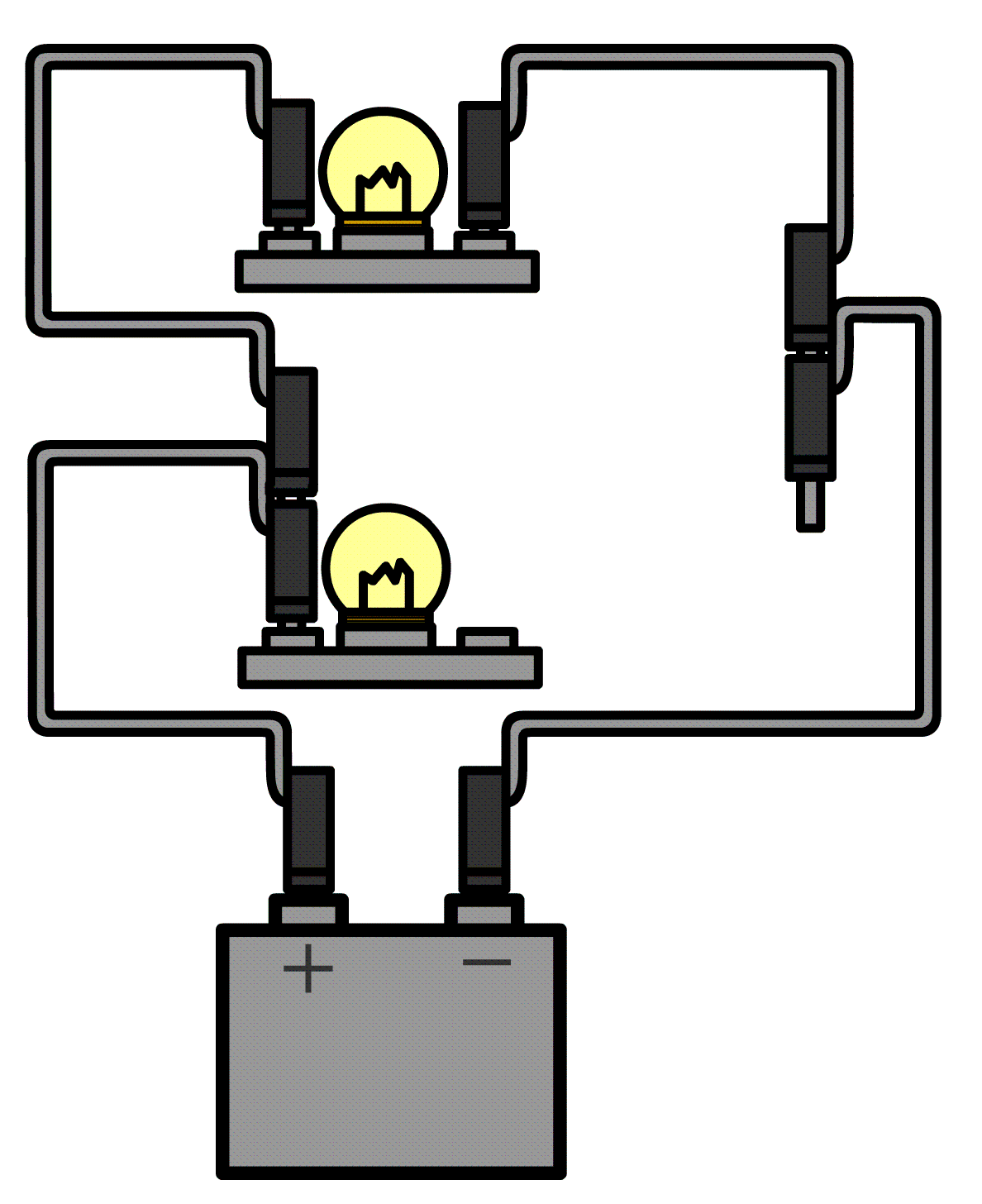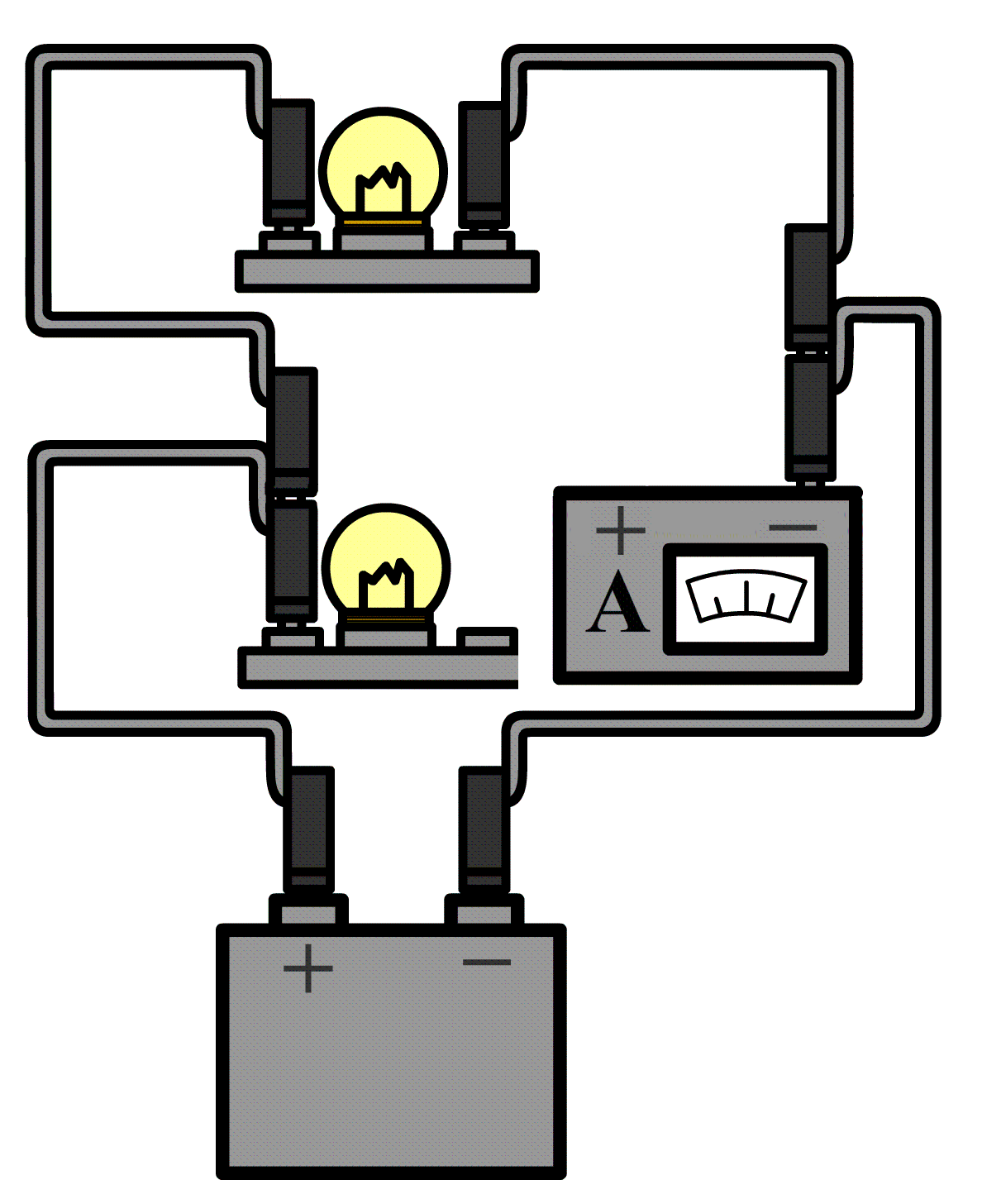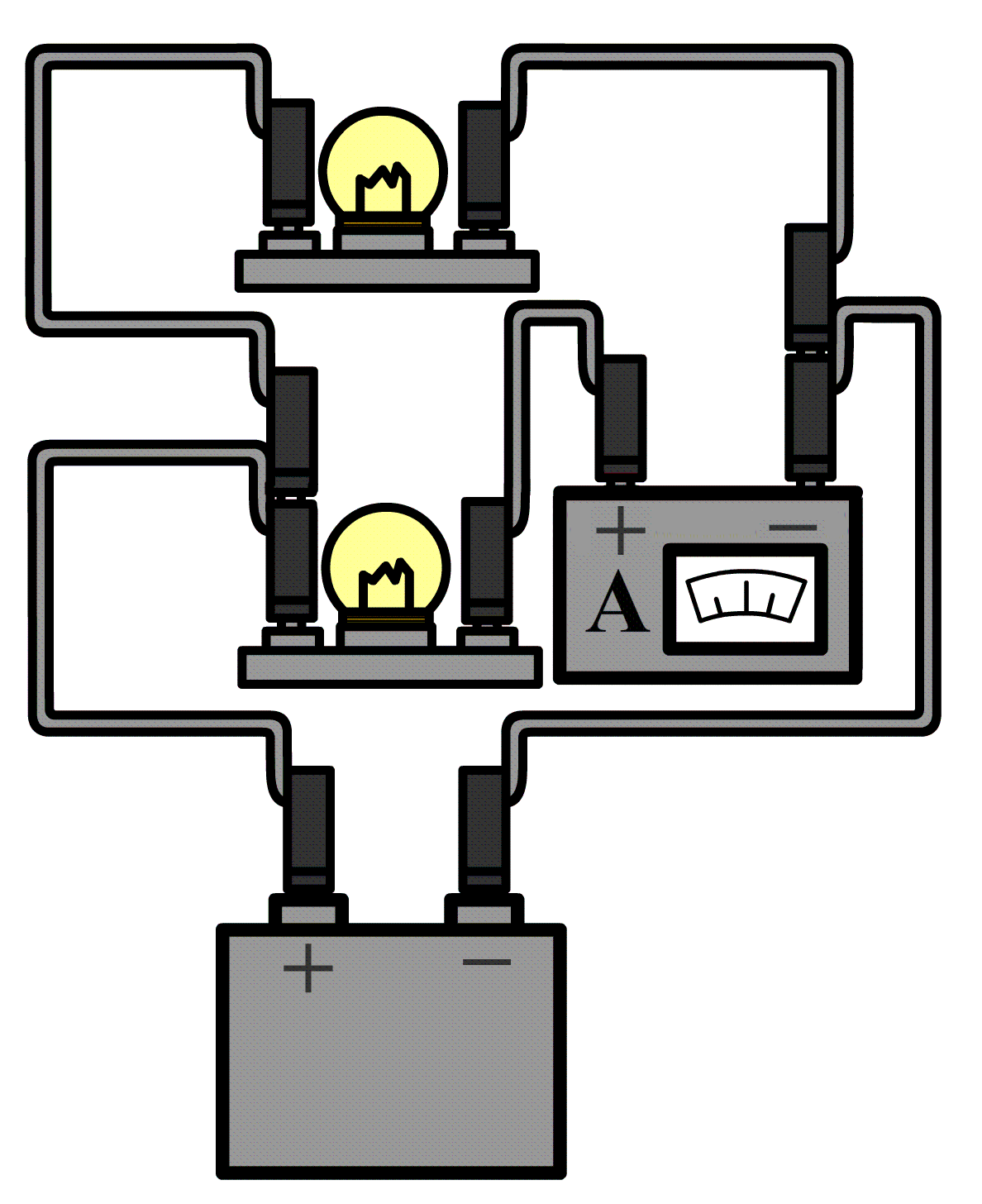
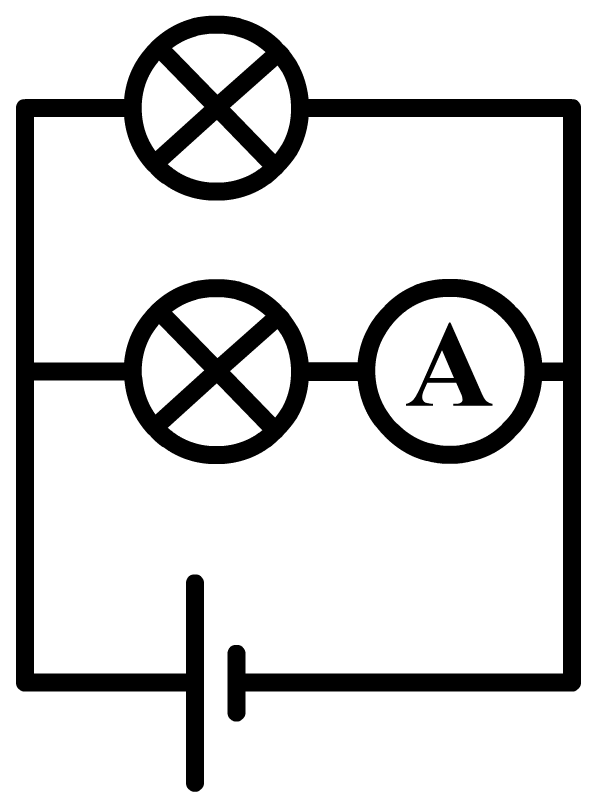
Hieronder meten we de stroomsterkte door de onderste lamp in een parallelschakeling. In dit geval zitten er aan weerszijden van de onderste lamp twee draden. Haal aan één kant beide draden los en sluit de ampèremeter dan hiertussen aan.
Hieronder zien we een stroommeter van dichtbij. Zoals je ziet zijn er in dit geval twee schaalverdelingen weergegeven. Welke je moet aflezen hangt af van hoe je de draden aansluit. Eén van de draden die je op de stroommeter aansluit gaat in de zwarte ingang en de ander gaat in één van de rode ingangen. In dit geval is de ingang genaamd "0,6 A" gebruikt. Dit betekent dat we de schaal moeten aflezen die eindigt op 0,6 A. Laten we nu de stroommeter aflezen. De wijzer zit in dit geval tussen de 0,3 A en de 0,4 A in. Tussen de 0,3 A en 0,4 A zitten nog vijf stapjes. Elk stapje komt dus overeen met 0,1 / 5 = 0,02 A. De wijzer geeft in dit geval dus 0,32 A aan (ga dit zelf na!).
Een ander meetinstrument dat je moet kunnen gebruiken is de multimeter. Hiermee kan zowel de stroomsterkte als de spanning worden gemeten en soms ook nog andere grootheden. Welke grootheid je wilt meten bepaal je met behulp van een draaiknop (zie de onderstaande afbeelding). Zoals je kunt zien moet je ook kiezen tussen wisselspanning (˜) en gelijkspanning (=). Onderaan zien we bijvoorbeeld zes verschillende standen waarmee de stroomsterkte in ampère bij wisselspanning gemeten kan worden. De verschillende waarden komen overeen met de maximale waarde die de meter in die stand kan aflezen. We zien hier 10 A, 2 A, 200 mA, 20 mA, 2 mA en 200 μA.
(Afbeelding: Examen VMBO-T, 2018-2)
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§3 De spanning
In deze paragraaf voegen we het begrip spanning toe. De spanning vertelt ons hoeveel energie ladingen uitgeven als ze door een stroomkring stromen.
De negatieve ladingen in de spanningsbron worden naar de pluspool getrokken. Deze aantrekkingskracht geeft ladingen de energie om door de schakeling te stromen. De spanning (U) die over een spanningsbron staat vertelt ons hoeveel energie elke lading meekrijgt. Deze energie wordt daarna weer uitgegeven in de andere onderdelen in de schakeling. We meten de spanning in volt (V).
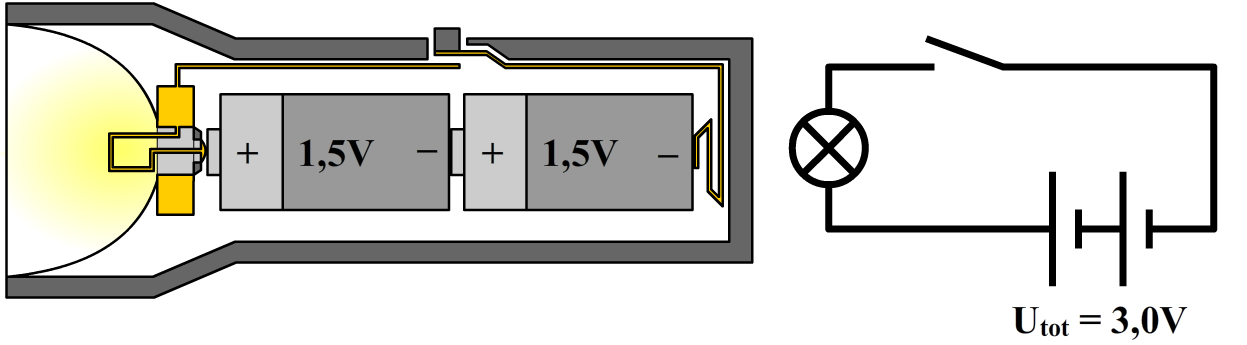
De meeste spanningsbronnen hebben een vaste spanning. Over een stopcontact staat bijvoorbeeld in Nederland altijd 230 V. We noemen dit ook wel de netspanning. Een normale AA-batterij heeft een spanning van 1,5 V. We kunnen ook spanningsbronnen aan elkaar koppelen. Hieronder zien we bijvoorbeeld twee AA-batterijen die in serie gekoppeld zijn. De totale spanning van beide batterijen samen is dan gelijk aan een optelling van de twee spanningen. In dit geval wordt dit 1,5 + 1,5 = 3,0 V.
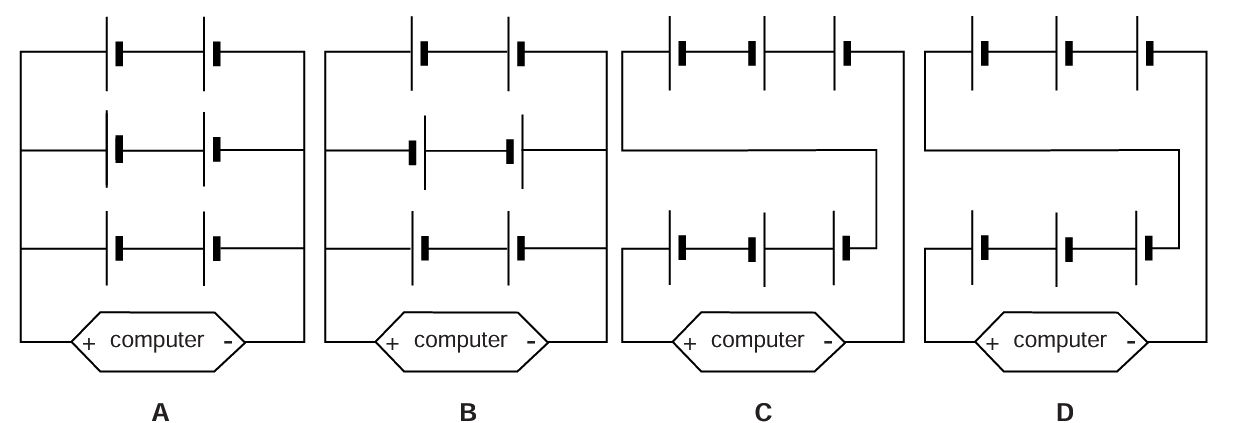
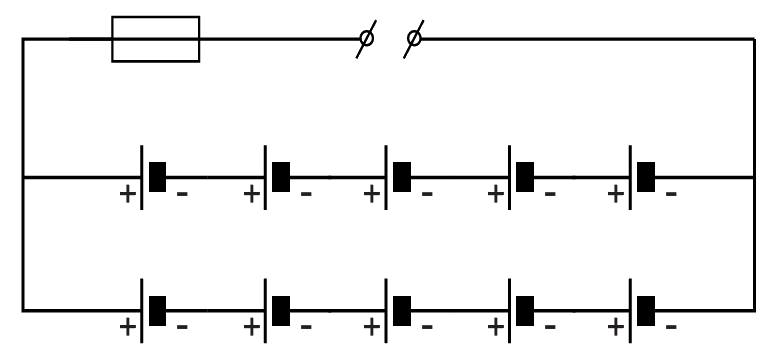
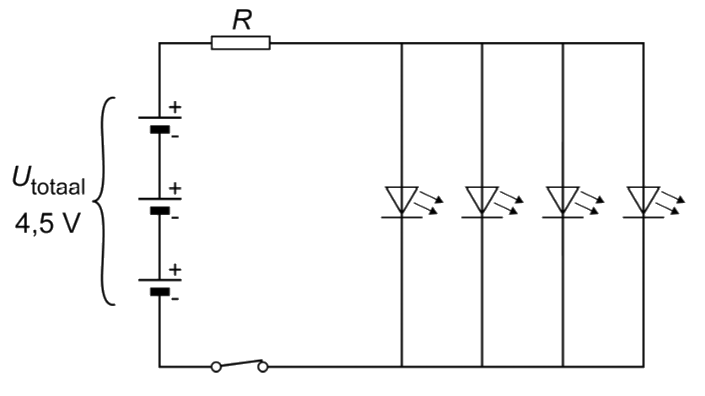
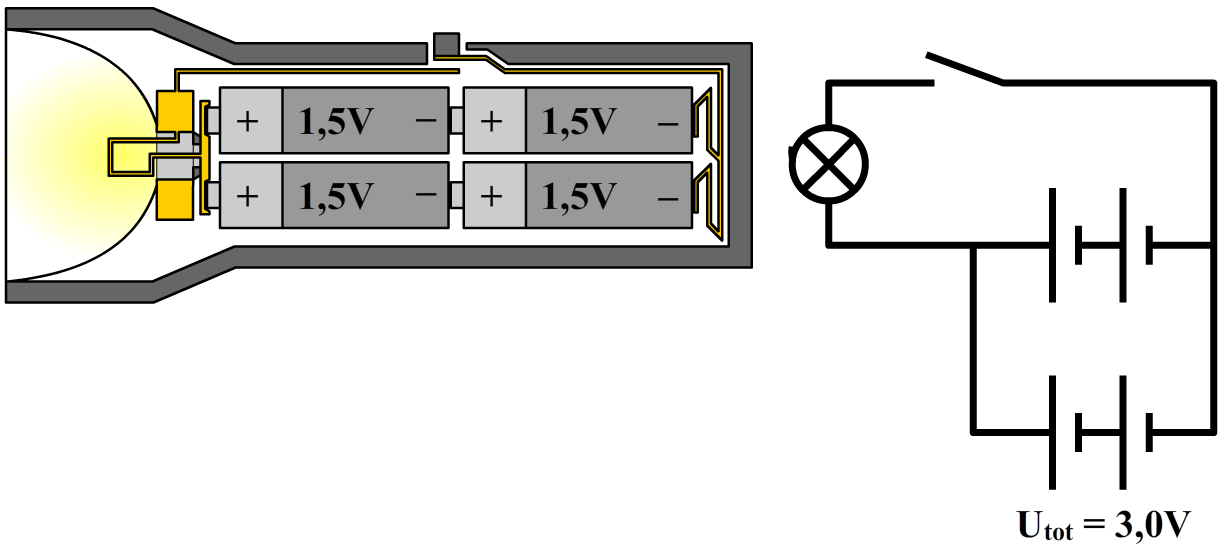
In sommige gevallen worden batterijen ook parallel geplaatst. Dit zien we in de onderstaande schakeling. We zien hier twee keer twee batterijen in serie die parallel aan elkaar gekoppeld zijn. Beide paren hebben een totale spanning van 1,5 + 1,5 = 3,0 V. Bij het parallel plaatsen van batterijen wordt de totale spanning niet groter. De totale spanning van de vier batterijen die hier zijn weergegeven is dus ook 3,0 V. De stroomsterkte neemt door de twee extra batterijen wel toe.
Laten we nu eens kijken hoe het zit met de spanning in een aantal verschillende schakelingen. Hieronder zien we een serieschakeling. Elke lading gaat in deze schakeling door beide lampjes heen. Elke lading zal zijn energie dus verdelen over twee lampjes. In dit geval zien we dat over de batterij 20 volt staat. Deze 20 volt wordt uitgegeven in de twee lampjes. Hoe de spanning precies verdeelt, hangt af van de weerstand van de lampjes. In dit geval is de weerstand van beide lampjes gelijk en vinden we over elk lampje een spanning van 10 volt.
In de onderstaande animatie zien we een parallelschakeling. Hier gaat elke lading maar door één lampje heen. Elke lading besteedt dus al zijn energie in slechts één lampje. De spanning over elk onderdeel in een parallelschakeling is dus gelijk.
De spanning meten we met een zogenaamde voltmeter (ook wel spanningsmeter genoemd). De voltmeter sluit je parallel aan over het onderdeel waarvan je de spanning wilt meten. Dit doe je door de voltmeter aan beide kanten van een onderdeel aan te sluiten. In de onderstaande afbeelding doen we dit voor een lampje.
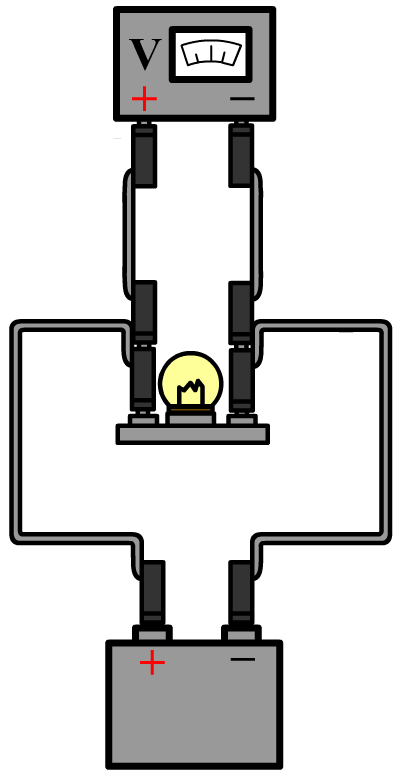
Hier doen we hetzelfde voor een lampje in een serieschakeling en een parallelschakeling:
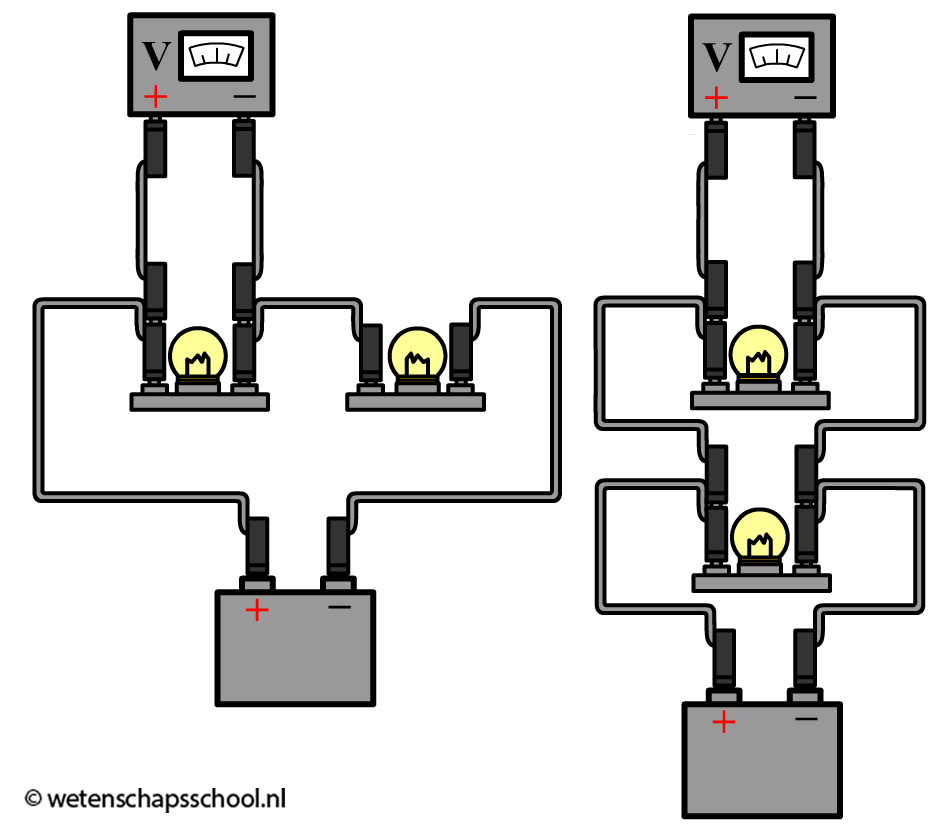
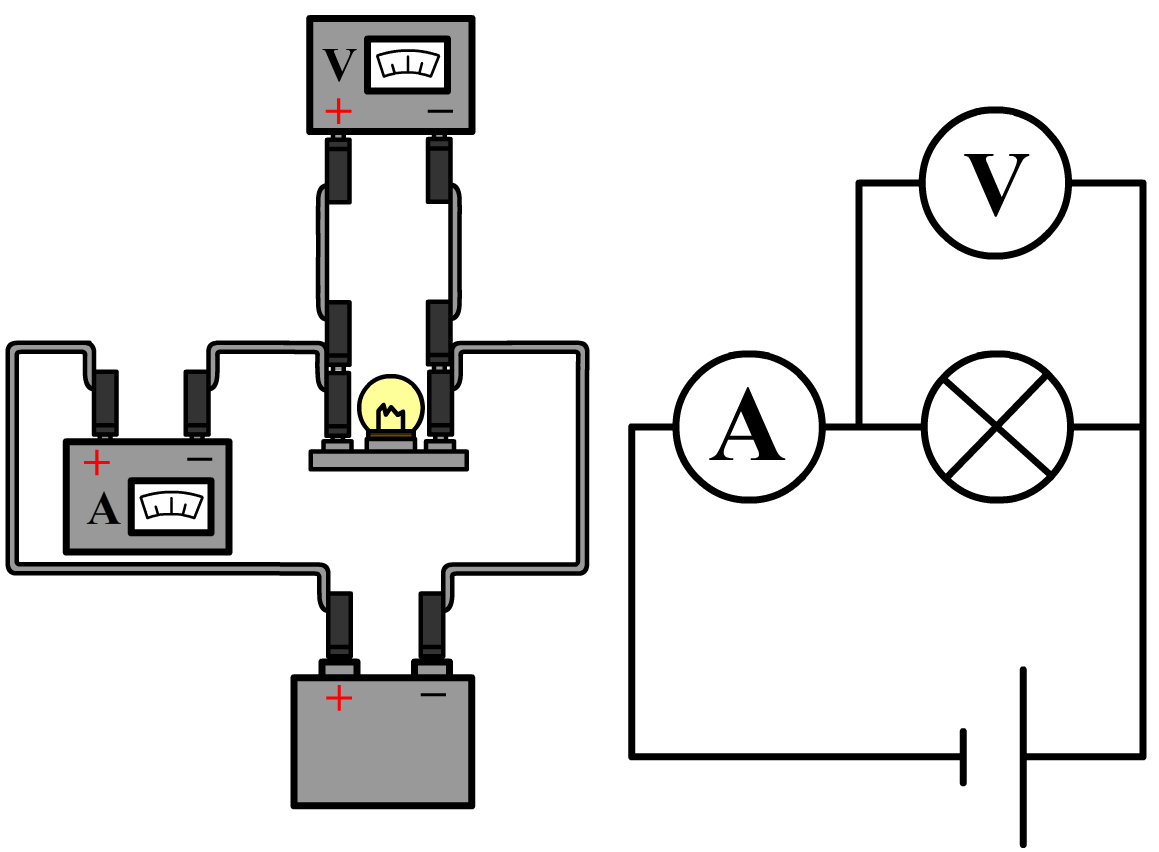
In de onderstaande afbeelding is zowel een spanningsmeter als een stroommeter aangesloten. Links zien we een realistische weergave van de schakeling en rechts een schematische versie.
|
Demonstratievideo
| ||
|
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
INSTRUCTIE:
Spanning en Stroomsterkte
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§4 De wet van Ohm
In deze paragraaf introduceren we de wet van Ohm. Hiermee kunnen we de weerstand van elektrische componenten uitrekenen.
De weerstand (R) van een onderdeel in een schakeling kunnen we berekenen met de wet van Ohm:
$$ R = \frac{U}{I} $$
|
Let er op dat je deze formule alleen toepast op een enkel onderdeel. Je kan bijvoorbeeld niet de spanning van de spanningsbron delen door de stroomsterkte van een lampje. Om goed bij te houden bij welk onderdeel de verschillende meetwaarden horen, is het handig de schakeling uit de vraag uit te tekenen en de waarden bij het juist onderdeel te schrijven.
Let er ook op dat als je deze formule toepast op de spanningsbron, dat je dan niet de weerstand van de spanningsbron vindt, maar de totale weerstand van de gehele schakeling. De (ideale) spanningsbron heeft namelijk helemaal geen weerstand.
Als je de formule omschrijft in de vorm "I = U/R", dan kan je ook zien dat bij gelijke spanning een kleinere weerstand zorgt voor een grotere stroomsterkte. Dit is goed te begrijpen. Hoe kleiner de weerstand, hoe gemakkelijker een materiaal lading doorlaat en hoe groter de stroomsterkte dus is.
|
Voorbeeld
|
|
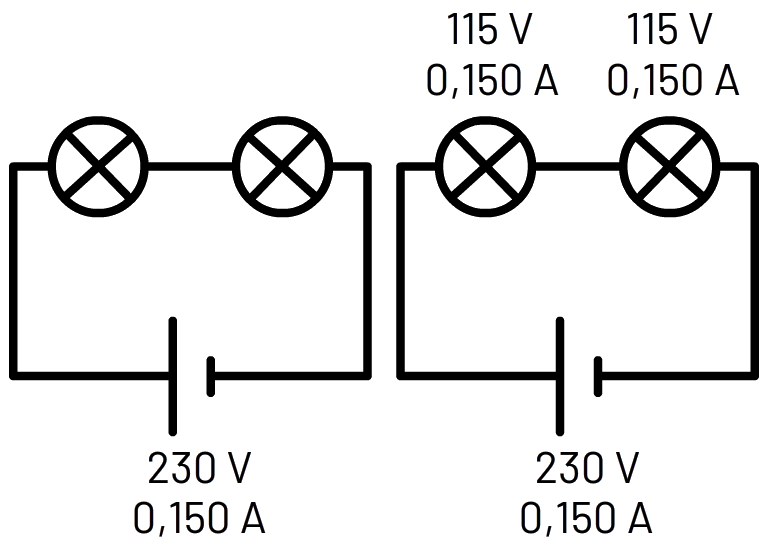
Vraag: Twee dezelfde lampjes in serie worden aangesloten op de netspanning. De stroomsterkte die de spanningsbron levert is gelijk aan 150 mA. Bereken de stroomsterkte door elk van de lampjes in ampère en de spanning over elk lampje in volt. Antwoord: Het is verstandig altijd eerst de schakeling even te tekenen en de waarden uit de vraag op de juist plek te zetten (zie de afbeelding linksonder). In een serieschakeling weten we dat de stroomsterkte overal gelijk is. Voor elk lampje geldt dus een stroomsterkte van 150 mA. Dit is gelijk aan 150 / 1000 = 0,150 A. Er geldt dus: Ilampje = 0,150 A In een serieschakeling verdeelt deze spanning zich over de lampjes. Omdat het hier om twee dezelfde lampjes gaat, weten we dat de spanning zich gelijk zal verdelen. Ook weten we dat de lampjes zijn aangesloten op de netspanning. De netspanning is in Nederland altijd gelijk aan 230 V. Over elk lampje staat dus een spanning van 230 / 2 = 115 V. Ulampje = 115 V
Vraag: Bereken de weerstand van elk lampje. Antwoord: Met de gegevens uit de vorige vraag kunnen we met de wet van Ohm de weerstand berekenen. Voor elk lampje geldt: $$ R = \frac{U}{I} $$ $$ R =\frac{115}{0,150}= 767 \text{ }Ω $$
|
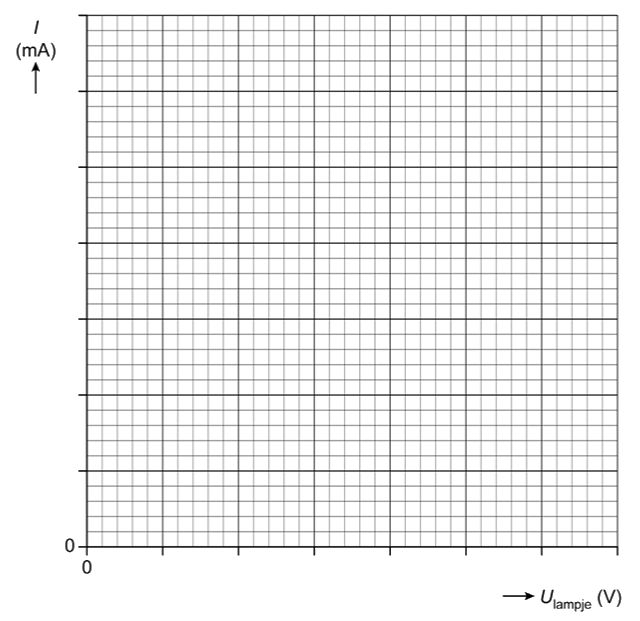
In een (U,I)-diagram kan je de weerstand van een onderdeel bestuderen bij verschillende spanningen. Bij een rechtevenredig verband (een rechte lijn door de oorsprong) spreken we van een ohmse weerstand. In dit geval is de weerstand bij alle spanningen constant. Onderdelen waarvoor dit niet geldt noemen we niet-ohmse weerstanden.
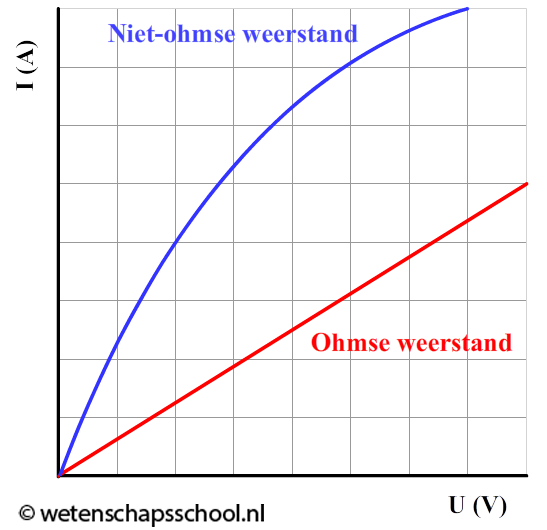
Hieronder zien we een foto van een vaste weerstand. Op de weerstand zijn gekleurde bandjes weergegeven. Deze kleuren vertellen ons hoeveel ohm de weerstand heeft. Rechts zie je welke waarden overeenkomen met welke kleuren. Deze afbeelding is ook in BINAS te vinden. In het onderstaande voorbeeld zien we een bruin, een zwart en een rood bandje. Dit komt volgens BINAS overeen met "1", "0", en "2" (ga dit zelf na!). De eerste twee cijfers vormen samen "10" en het laatste cijfer geeft aan met welke tienmacht je dit getal moet vermenigvuldigen. In dit geval dus met "102". De waarde van de weerstand is dus 10 × 102 Ω, oftewel, 1000 Ω. Aan de rechterzijde is ook een goud bandje te zien. Dit vertelt ons dat de waarde 5% kan afwijken.
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
INSTRUCTIE:
De wet van Ohm
INSTRUCTIE:
De LED
|
Leerdoelen:
|
|
|
Opdrachten
| ||||||||||||||||
|
§5 Vervangingsweerstand
In deze paragraaf gaan we leren de totale weerstand van een schakeling te bepalen. We doen dit met het concept vervangingsweerstand.
Eerder in dit hoofdstuk hebben we gelezen dat de spanningsbron zelf geen weerstand heeft. Als we de wet van Ohm toepassen op de spanningsbron, dan vinden we in plaats daarvan de totale weerstand van de schakeling, ook wel de vervangingsweerstand (Rv) genoemd. We kunnen deze weerstand ook berekenen met behulp van de weerstand van de individuele onderdelen. In de onderstaande afbeelding zien we bijvoorbeeld links twee weerstanden in serie. Rechts zijn deze twee weerstanden vervangen door één vervangingsweerstand.
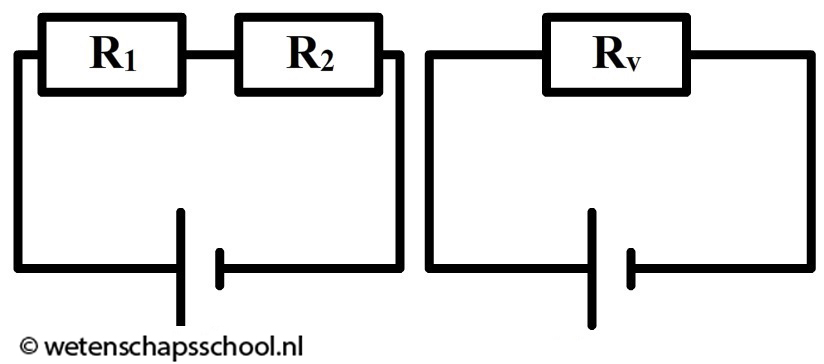
De vervangingsweerstand van twee weerstanden in serie is gelijk aan:
$$ R_v = R_1 + R_2 \;\;\;\;\;\;\;\;\;\; \mathrm{(serie)} $$
|
|
Voorbeeld
|
|
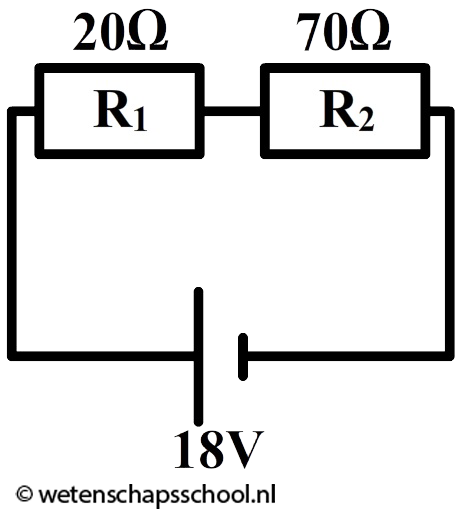
Vraag: In een serieschakeling zijn twee weerstanden opgenomen. Eén van de weerstanden heeft een waarde van 20 Ω en de ander van 70 Ω. De spanning over de spanningsbron is 18 V. Bereken de stroomsterkte die de spanningsbron levert. Antwoord: Eerst tekenen we de schakeling en zetten we de gegevens uit de vraag bij de juiste onderdelen:
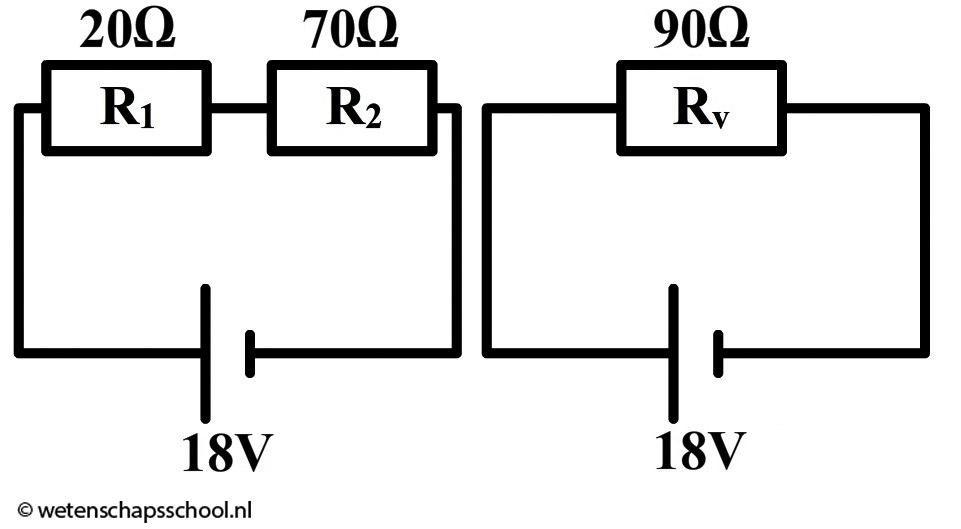
Dan berekenen we de vervangingsweerstand: $$ R_v = R_1 + R_2 $$ $$ R_v = 20 + 70 = 90 \;\Omega $$Met de vervangingsweerstand is de schakeling simpeler geworden (zie de onderstaande rechter afbeelding). Als gevolg kunnen we nu de stroomsterkte van de spanningsbron uitrekenen: $$ I = \frac{U}{R} $$ $$ I = \frac{18}{90} = 0,20 \text{ A} $$
|
Ook van twee parallelle weerstanden kunnen we de vervangingsweerstand berekenen.
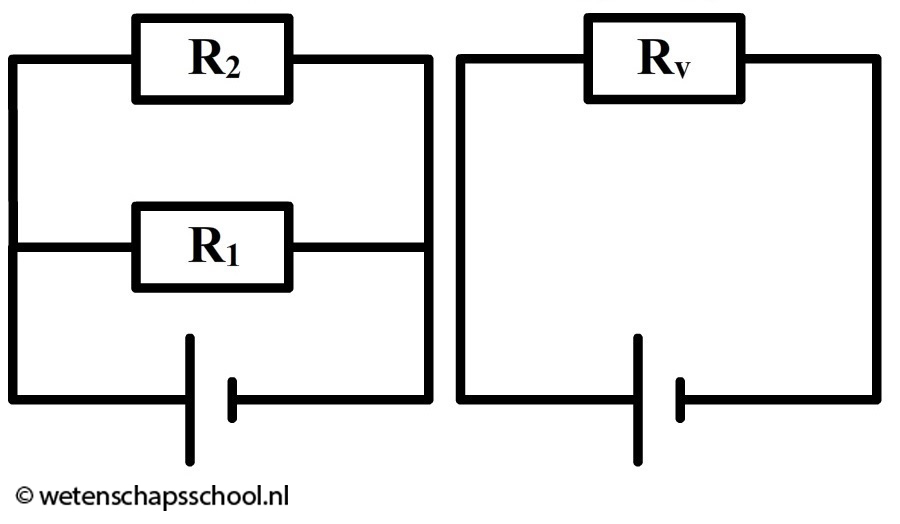
In dat geval geldt:
| $$ \frac{1}{R_v} = \frac{1}{R_1} + \frac{1}{R_2} \;\;\;\;\;\;\;\;\;\; \mathrm{(parallel)} $$ |
In het onderstaande voorbeeld leer je hoe je deze formule kan gebruiken:
|
Voorbeeld
|
|
Vraag: In een parallelschakeling zijn twee lampjes opgenomen. Eén van de lampjes heeft een weerstand van 20 Ω en het andere lampje heeft een weerstand van 50 Ω. Bereken de vervangingsweerstand van deze schakeling. Antwoord: We rekenen de vervangingsweerstand als volgt uit. We beginnen met het invullen van de formule: $$ \frac{1}{R_v} = \frac{1}{R_1} + \frac{1}{R_2} $$ $$ \frac{1}{R_v} = \frac{1}{20} + \frac{1}{50} $$De rechterzijde van de formule kunnen we nu uitrekenen. We vinden: $$ \frac{1}{R_v} = 0,07 $$Nu kunnen we deze formule omschrijven, zodat we Rv vinden: $$ R_v = \frac{1}{0,07} = 14 \;\Omega $$De vervangingsweerstand van de parallelschakeling is dus 14 Ω.
|
Zoals je in het vorige voorbeeld kunt zien, is de vervangingsweerstand bij een parallelschakeling kleiner dan de weerstanden van de componenten! Dit klinkt verrassend, maar dit is goed te begrijpen. Door twee parallelle weerstanden gaat namelijk meer stroom dan door één afzonderlijke weerstand. De vervangingsweerstand laat dus meer ladingen door dan de afzonderlijke onderdelen en heeft dus een kleinere weerstand! Het is belangrijk dat je dit onthoudt.
|
Demonstratievideo
| ||
|
|
Leerdoelen:
|
|
|
Opdrachten
|
|
§6 Het vermogen
Met de spanning en de stroomsterkte kunnen we ook het vermogen berekenen. Het vermogen vertelt ons hoeveel energie een onderdeel in een schakeling per seconde verbruikt. In deze paragraaf bespreken we verschillende manieren om met het vermogen te rekenen.
Het vermogen (P) vertelt ons hoeveel energie een onderdeel in een schakeling per tijdseenheid verbruikt. De SI-eenheid van het vermogen is de watt (W) en dit is gelijk aan de hoeveelheid joule per seconde. Voor het vermogen geldt:
$$ P = U \times I $$
|
Met behulp van het vermogen kunnen we ook de totale energie (E) uitrekenen die een onderdeel van de schakeling verbruikt heeft. Er geldt:
$$ E = P \times t $$
|
Naast de joule is het ook mogelijk om als eenheid voor de energie de kilowattuur (kWh) te gebruiken. In dat geval moeten we het vermogen in kilowatt (kW) invoeren en de tijd in uren (h):
$$ E = P \times t $$
|
Merk op dat kilowattuur niet hetzelfde is als "kilowatt per uur". Kilowattuur is net als joule gewoon een maat voor de energie.
In de meterkast bevindt zich een kWh-meter waar het gebruik van elektriciteit in huis wordt bijgehouden. Op basis hiervan wordt door de energieleverancier bepaald hoe hoog de elektriciteitsrekening is.
|
Voorbeeld
|
|
Vraag: Een wasmachine met een vermogen van 2500 W staat elke week twee uur aan. Elke kWh aan energie kost 0,20 euro. Bereken hoeveel het kost om deze wasmachine een jaar te gebruiken. Antwoord: Omdat we het aantal kilowattuur (kWh) willen bereken, moeten we het vermogen eerst omrekenen naar kilowatt (kW): P = 2500 / 1000 = 2,5 kW Nu rekenen we uit hoeveel uur de wasmachine per jaar aanstaat. Volgens de vraag staat de wasmachine elke week twee uur aan en er zitten 52 weken in een jaar. In totaal vinden we: t = 52 × 2 = 104 uur Nu vullen we de formule in: $$ E = Pt $$ $$ E = 2,5 \times 104 = 260 \text{ kWh} $$Elke kilowattuur (kWh) kost volgens de vraag 0,20 euro. In dit geval zijn de kosten dus: 260 × 0,20 = 52 euro De elektriciteit voor de wasmachine kost elk jaar dus 52 euro.
|
|
Voorbeeld
|
|
Vraag: Een lamp is aangesloten op de netspanning. Door het lampje gaat een stroomsterkte van 0,30 A. De kWh-prijs is 0,24 euro. Bereken hoeveel het kost om het lampje 4,0 dagen te laten branden. Bereken hiervoor eerst het vermogen van de lamp. Antwoord: De stroomsterkte is gelijk aan: I = 0,30 A De netspanning is in Nederland gelijk aan 230 V: U = 230 V Met deze gegevens kunnen we het vermogen uitrekenen: $$ P = U \times I $$ $$ P = 230 \times 0,30 = 69 \text{ W} $$Nu berekenen we hoeveel het kost om het lampje 4,0 dagen te laten branden. Hiervoor berekenen we eerst de verbruikte energie in kWh. Hiervoor hebben we het vermogen in kW nodig: P = 69 / 1000 = 0,069 kW De tijd willen we in uren weten. De lamp staat 4,0 dagen aan en er zitten 24 uren in een dag. Er geldt dus: t = 4 × 24 = 96 h Nu kunnen we de energie uitrekenen: $$ E = P \times t $$ $$ E = 0,069 \times 96 = 6,624 \text{ kWh} $$6,624 × 0,24 = 1,59 euro De elektriciteit voor de lamp kost dus 1,59 euro.
|
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
↓ VMBO VERSIES van deze VIDEOS komen binnenkort online!
INSTRUCTIE:
Vermogen
|
Leerdoelen:
|
|
|
Opdrachten
|
|
| BINAS: | |
| 7-12 | Formules |
| 13 | Kleurcodes weerstanden |
| 14 | Symbolen elektrische schakelingen |
| 18 | Rendementen |