Hoofdstuk 3
Radioactiviteit
§1 Kernverval §2 Halveringstijd §3 Activiteit §4 Stralingsgevaar
§1 De bouw van atomen
In dit hoofdstuk gaan we bestuderen wat radioactiviteit precies is en wat de gevaren zijn. Ook gaan we een aantal medische toepassingen bestuderen. Voordat we dit alles kunnen begrijpen, moeten we eerst atoomkernen bestuderen. Dat gaan we in deze eerste paragraaf doen.
In een eerder hoofdstuk hebben we geleerd dat materie is opgebouwd uit atomen. Atomen blijken ook weer opgebouwd uit kleinere deeltjes. Elk atoom heeft in zijn centrum een atoomkern, bestaande uit positief geladen deeltjes die we protonen noemen en neutrale deeltjes die we neutronen noemen. Om de kern heen bevindt zich een wolk van negatieve geladen deeltjes die we elektronen noemen. Elk atoom bevat evenveel protonen als elektronen en als gevolg zijn atomen neutraal.
Zoals je in de bovenstaande afbeelding kunt zien, bewegen de elektronen niet willekeurig om de atoomkern. De elektronen bevinden zich op vaste afstanden van de kern. Deze vaste afstanden noemen we schillen. In de binnenste schil passen slechts twee elektronen, in de tweede schil passen 8 elektronen en in de derde schil passen wel 18 elektronen. Het zwaarste atoom dat we kennen heeft wel zeven schillen met daarin 118 elektronen.
Hieronder zien we de eerste 8 atomen uit het periodiek systeem. Waterstof bestaat uit één proton en dus ook één elektron. Helium bestaat uit twee protonen en dus ook twee elektronen. Lithium bevat drie protonen en dus ook drie elektronen, maar omdat de eerste schil vol is, komt het derde elektron in de tweede schil terecht. Op deze manier zijn alle atomen uit het periodiek systeem opgebouwd.
Het aantal protonen in een atoom noemen we het atoomnummer. In het onderstaande periodiek systeem vind je het atoomnummer linksonder de symbolen. Het is belangrijk te onthouden dat voor elke atoomsoort het atoomnummer vast staat. IJzer heeft bijvoorbeeld altijd atoomnummer 26 (ga dit zelf even na met behulp van de onderstaande afbeelding).
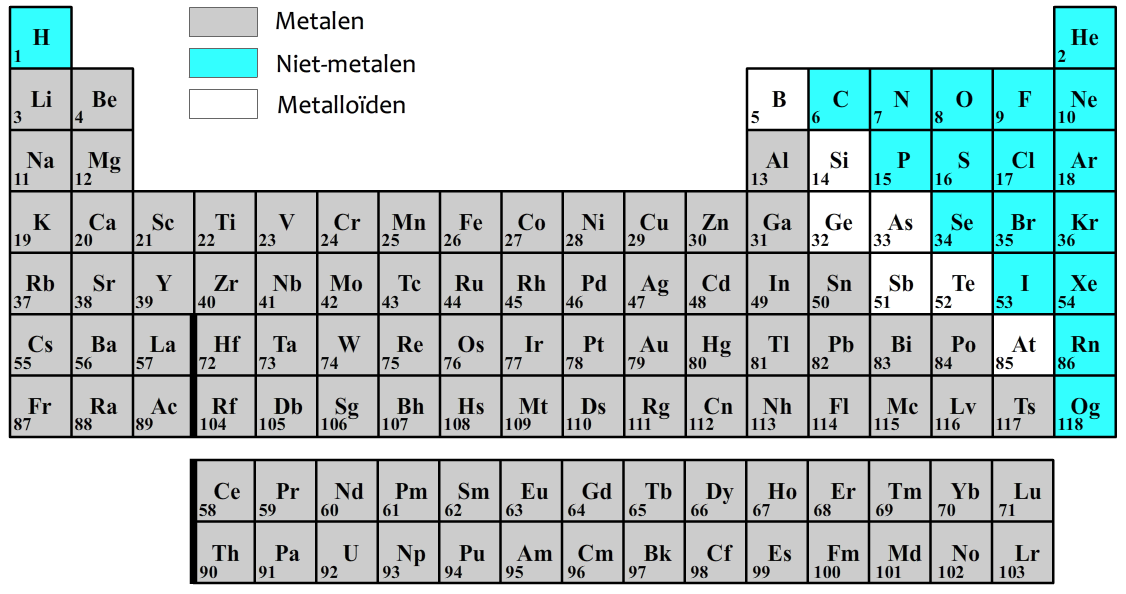
Het aantal protonen en neutronen samen noemen we het massagetal. Het massagetal wordt vaak achter de naam van het element genoemd. Fluor-19 heeft dus een massagetal van 19. Omdat fluor volgens het bovenstaande periodiek systeem 9 protonen heeft, moet het dus ook nog 10 neutronen bevatten, zodat het aantal protonen en neutronen samen 9 + 10 = 19 wordt. Waterstof-1 heeft een atoomnummer van 1 en bevat dus slechts 1 proton. Het massagetal van waterstof is ook 1, dus waterstof bevat 0 neutronen (omdat 1 + 0 = 1).
Het massagetal wordt ook geregeld linksboven het symbool van het element genoemd. Het atoomnummer en massagetal schrijven we dan als volgt op:
$$^{\;\;\;\text{ massagetal}}_{\text{atoomnummer}}\text{Element}$$Het massagetal van een atoomsoort staat niet vast. Zo heb je bijvoorbeeld koolstof-12 en koolstof-14. In het periodiek systeem kunnen we zien dat koolstof altijd 6 protonen in de kern heeft. Om op het juiste massagetal uit te komen moet koolstof-12 nog 6 neutronen in de kern hebben (want 6 + 6 = 12) en moet koolstof-14 nog 8 neutronen in de kern hebben (want 6 + 8 = 14). Atomen met hetzelfde aantal protonen, maar met een verschillend aantal neutronen noemen we isotopen. Koolstof-12 en koolstof-14 zijn dus twee isotopen van koolstof.
$$^{12}_{\;6}C \;\;\;\;\;\; ^{14}_{\;6}C$$Ook het proton, het neutron en het elektron kunnen we in deze notatie opschrijven. Het proton bestaat uit 1 proton en 0 neutronen, dus het atoomnummer is 1 en het massagetal is ook 1. Het neutron bestaat uit 0 protonen en 1 neutron, dus het atoomnummer is 0 en het massagetal is 1. Het elektron vormt een uitzondering op de regel. Een elektron bevat natuurlijk 0 protonen, maar omdat het een lading van -1 heeft, zeggen we dat het atoomnummer -1 heeft. Het massagetal van een elektron is 0.
| $$^1_1p \;\;\;\;\;\;\;\; ^1_0n \;\;\;\;\;\;\;\; ^{\;\;0}_{-1}e$$ |
Leerdoelen:
| ||
|
§1 Kernverval
Nu we begrijpen waaruit atomen bestaan, kunnen de radioactiviteit begrijpen. We doen dit aan de hand van het begrip kernverval.
We spreken van een kernreactie als de atoomkern een verandering ondergaat. Een voorbeeld van een kernreactie is kernverval. Dit is het spontaan uit elkaar vallen van een atoomkern. Stoffen waarbij dit gebeurt noemen we radioactief. Bij kernverval schiet er vaak een deeltje met behoorlijke snelheid uit het atoom weg. We noemen dit straling. Als een atoom straling uitgezonden heeft, dan zeggen we dat het atoom vervallen is. De oorspronkelijke radioactieve kern noemen we de moederkern en de kern die na de straling overblijft noemen we de dochterkern. In sommige gevallen zijn de dochterkernen zelf ook weer radioactief. Er bestaan ook atoomkernen die geen straling uitzenden. We noemen deze isotopen stabiel.
Het is belangrijk goed onderscheid te maken tussen kernreacties en chemische reacties. Bij een chemische reactie worden elektronen tussen atomen uitgewisseld of gedeeld. De kernen van de atomen blijven bij chemische reacties onaangetast. Bij kernreacties is het juist de kern die verandert.
Er kunnen bij kernreacties drie soorten straling vrijkomen. Welk type straling wordt uitgezonden door welke isotoop kan je vinden in BINAS. De eerste soort wordt alfastraling genoemd. Hierbij breekt een helium-4-kern af van de kern van een atoom. Een helium-4-kern bevat twee protonen en twee neutronen:
| $$^4_2He \;\;\;\;\;\;\;\; (\alpha)$$ |
Hier zien we een voorbeeld van een vervalvergelijking waarbij α-straling vrijkomt. Het gaat hier om het verval van polonium-214:
$$^{214}_{84}\text{Po} \rightarrow ^{210}_{82}\text{Pb} + ^{4}_{2}\text{He}$$Let op dat de som van de atoomnummers voor de reactie gelijk is aan de som van de atoomnummers na de reactie. Hetzelfde geldt voor de massagetallen. Het behoud van atoomnummer is een gevolg van het behoud van lading. Het behoud van massagetal is het gevolg van het behoud van massa.
De tweede soort straling is bètastraling. Als we spreken van β-straling of β--straling dan komt er een elektron uit de kern.
| $$^{\;\;0}_{-1}e^- \;\;\;\;\;\;\;\; (\beta^- \; \text{of} \;\; \beta)$$ |
Maar hoe kan er een elektron uit de kern komen? In sommige gevallen kan een neutron vervallen in een proton. Hier komt dan een elektron bij vrij:
$$^{1}_{0}\text{n} \;\rightarrow\; ^{1}_{1}\text{p} \;+\; ^{0}_{-1}\text{e}^-$$Hieronder zien we een voorbeeld van een vervalvergelijking waar β--straling bij vrijkomt:
$$^{40}_{19}\text{K} \;\rightarrow\; ^{40}_{20}\text{Ca} \;+\; ^{0}_{-1}\text{e}^-$$De laatste soort straling is gammastraling (γ-straling). Gammastraling bestaat uit lichtdeeltjes, ook wel fotonen genaamd, met een frequentie buiten het zichtbare spectrum. We schrijven:
| $$^0_0\gamma$$ |
Met een zogenaamd nevelvat kunnen we verschillende soorten straling zichtbaar maken. Als een deeltje door dit vat schiet, botst het met de atomen in het vat en als gevolg worden deze atomen geïoniseerd. Om deze ionen vormen dan kleine druppeltjes die een zichtbaar spoor vormen. In dit filmpje kan je zowel de sporen van alfadeeltjes als betadeeltjes zien.
DEMO:
Nevelvat
In het onderstaande filmpje is een stukje radioactief uranium in een nevelvat gelegd. De alfastraling die hierbij vrijkomt is duidelijk te zien.
DEMO:
Nevelvat II
Tot nu toe hebben we het gehad over reacties die spontaan plaatsvinden. We kunnen kernreacties echter ook kunstmatig opwekken. Een voorbeeld is het beschieten van een uraniumatoom met een neutron. Het neutron wordt dan ingevangen door de kern, waarna de kern in een aantal stukken uiteenvalt. We noemen dit ook wel kernsplijting:
$$^{235}_{\;92}\text{U} \;+\; ^1_0\text{n} \;\rightarrow \;^{99}_{42}\text{Mo} \;+\; ^{134}_{\;50}\text{Sn} + 3^1_0\text{n}$$Zoals je kunt zien komen bij deze reacties weer nieuwe neutronen vrij en deze neutronen kunnen weer tegen andere uraniumatomen botsen. Als gevolg kan een kettingreactie op gang gebracht worden waarbij heel veel energie vrijkomt. Een gecontroleerde versie van zo'n kettingreactie vindt plaats in een kernreactor (en een ongecontroleerde versie bij het ontploffen van een kernbom). De werking van een kernreactor is hieronder aan de linker zijde simpel weergegeven. Het radioactieve materiaal, hier de kernbrandstof genoemd, zorgt ervoor dat een omringend gas wordt opgewarmd (hier in het geel aangegeven). Dit hete gas zorgt er op zijn beurt weer voor dat water aan de kook wordt gebracht. De stoom die hierbij ontstaat wordt gebruikt om een turbine te laten draaien waarmee elektriciteit wordt gegenereerd (dit deel is niet afgebeeld). Door middel van regelstaven, die in en uit de kernbrandstof kan worden geschoven, kan de reactie beperkt of juist versterkt worden. De toren die rechts is afgebeeld wordt gebruikt om het systeem te koelen, zodat het niet oververhit raakt. De nevel die aan de bovenzijde opstijgt bestaat uit water.
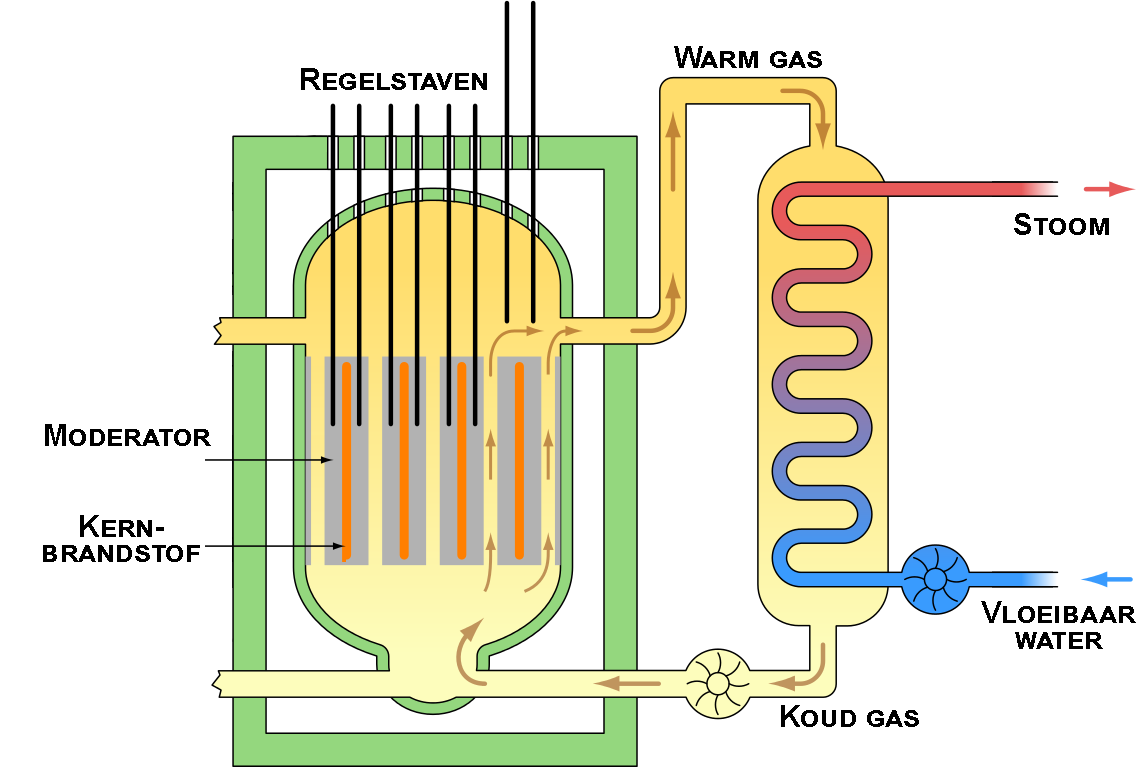
(Afbeelding: Emoscopes; CC BY-SA 3.0 / Bjoern Schwarz; CC BY 2.0)
Naast kernverval bestaat ook kernfusie. Hier fuseren atoomkernen samen. Ook bij dit proces kan energie vrijkomen. Dit gebeurt bijvoorbeeld in de zon. Hier wordt waterstof gefuseerd tot helium. De energie die hierbij vrij komt zorgt voor het licht dat de zon geeft.
INSTRUCTIE:
Radioactiviteit
INSTRUCTIE:
Kernreacties
Zorg dat je kan redeneren over straling en dat je begrijpt hoe een kerncentrale werkt
|
|
|
Zorg dat je kernvervalvergelijkingen kan opstellen
|
|
§2 Halveringstijd
In deze paragraaf gaan we bestuderen hoe het aantal radioactieve deeltjes in een bron afneemt in de tijd. We gebruiken hiervoor het begrip halveringstijd. Dit is de tijdsduur waarna de helft van de kernen vervallen is.
In de vorige paragraaf hebben we gezien dat radioactieve atoomkernen naar verloop van tijd straling uitzenden. Als dit gebeurt is, dan zeggen we dat het atoom vervallen is. De tijdsduur waarna de helft van de deeltjes in de bron vervallen is, noemen we de halveringstijd of de halfwaardetijd (t1/2).
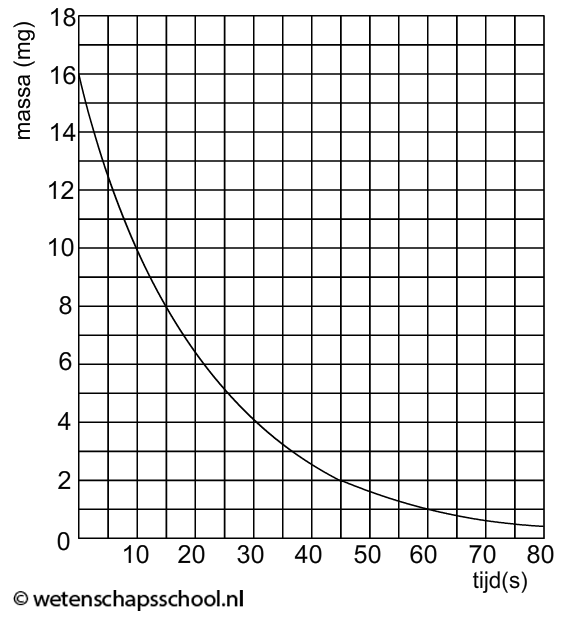
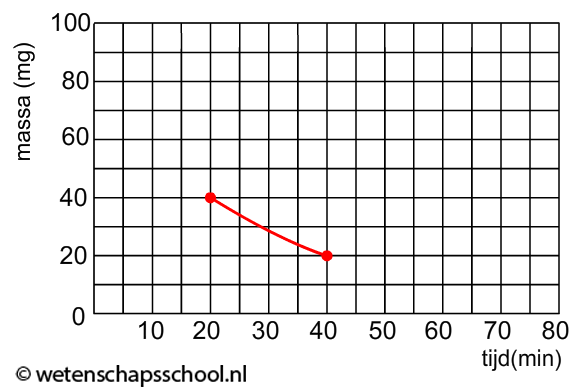
In het onderstaande (N,t)-diagram zien we het aantal radioactieve deeltjes in een bron (N) uitgezet tegen de tijd (t). In dit geval zien we dat het aantal radioactieve kerndeeltjes elke 10 uur halveert. Voor deze bron geldt dus een halveringstijd van 10 uur.
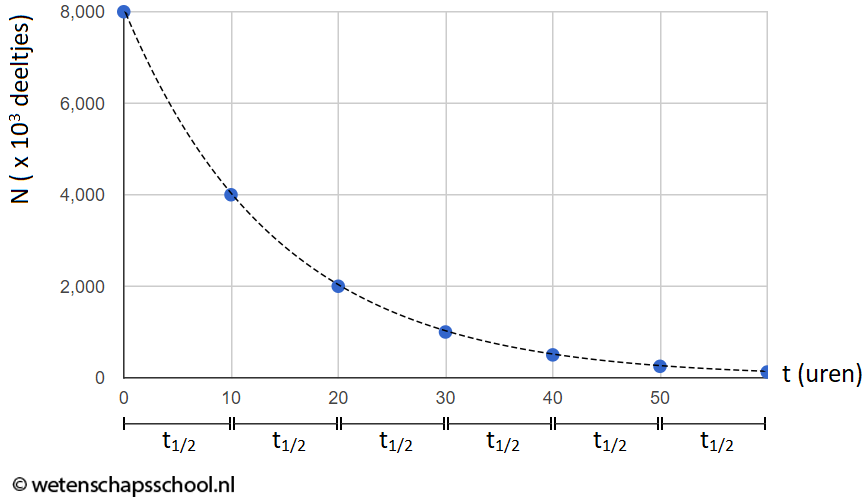
In het onderstaande programma zien we hoe deze grafiek zijn vorm krijgt. Elke keer als je op de knop "+1 halfwaardetijd" klikt, geldt voor elk radioactief deeltje (aangegeven met een zwarte cirkel) dat deze 50% kans heeft om te vervallen (een vervallen deeltje wordt weergegeven als een witte cirkel).
Elke radioactieve isotoop heeft zijn eigen halveringstijd en deze kan variëren van een fractie van een seconde tot miljoenen jaren. Voor een aantal isotopen is de halveringstijd te vinden in BINAS. In deze tabel vinden we bijvoorbeeld dat koolstof-14 een halveringstijd heeft van 5730 jaar. Na 5730 jaar is dus nog maar 50% van de koolstof-14 over. Na 2 × 5730 = 11 460 jaar is nog slechts 25% over en na 3 × 5730 = 17 190 jaar nog 12,5%. Etc.
Stel we hebben 20 gram van een radioactieve stof. Als we wachten tot bijvoorbeeld drie keer de halveringstijd van de stof voorbij is gegaan, dan is de 20 gram dus drie maal gehalveerd. We hebben dan zoveel gram over:
$$ 20 \text{ gram} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = 2,5 \text{ gram}$$Met het aantal halveringen (n) en de halveringstijd kunnen we uitrekenen hoelang deze halveringen geduurd hebben:
$$ t = t_{1/2} \times n $$
|
Doordat in deze formule twee tijden door elkaar worden gedeeld, ben je niet gebonden aan de seconde. Je kan beide tijden dus ook best in bijvoorbeeld dagen of jaren invullen.
De halveringstijd van stoffen kan o.a. gebruikt worden voor radiometrische datering. Dit is een techniek die gebruikt wordt om uit te vinden hoe oud voorwerpen zijn. Het bekendste voorbeeld hiervan is C14-datering. Koolstof-14 komt in vergelijking met andere koolstofisotopen in elk levend organisme in een vaste verhouding voor. Als een organisme echter sterft, komt er geen nieuwe koolstof-14 binnen, maar neemt de overgebleven koolstof-14 wel af door kernverval. Door te kijken hoeveel koolstof-14 er nog over is, kunnen we met de halveringstijd uitrekenen hoe lang geleden het organisme gestorven is. Stel dat in een oud houten beeldje slechts 6,25% van de C-14 deeltjes is overgebleven. Het aantal halveringen vind je op door 100% telkens met 1/2 te vermenigvuldigen:
$$ 100\% \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = 6,25 \% $$De 6,25% wordt dus behaald na 4 halveringen.
Met de halveringstijd van C-14 (t1/2 = 5730 j), vinden we dan hoe oud het beeldje moet zijn:
$$t = t_{1/2} \times n $$In dit geval blijkt het deeltje uit de Oude Steentijd te komen!
$$t = 5730 \times 4 = 22,9 \times 10^3 \text{ jaar}$$
INSTRUCTIE:
Halveringstijd
|
Zorg dat je de halveringstijd kan bepalen met een (N,t)-diagram en dat je kan rekenen met Nt = N0(1/2)n
|
|
§4 Stralingsgevaar en medische toepassingen
In deze paragraaf bestuderen we de gevaren van straling voor de mens en ook de positieve toepassingen van straling in het ziekenhuis.
Radioactieve deeltjes vind je overal om je heen. Ze zitten niet alleen in gesteentes in gebergten, maar ook in de muren van ons huis en zelfs in ons eten. Gelukkig gaat het in deze gevallen meestal om kleine hoeveelheden. We kunnen aantonen of een stof radioactief is met een geigerteller (zie de onderstaande afbeelding). Dit apparaat bestaat uit een buis met daarin een gas. Als straling het gas binnenkomt, dan worden een aantal atomen van het gas geïoniseerd. De vrijgemaakte elektronen zorgen dan voor een kleine stroom en deze stroom zorgt in een luidspreker voor een hoorbaar piepje. Hoe meer piepjes je hoort, hoe meer straling er in de buurt is.
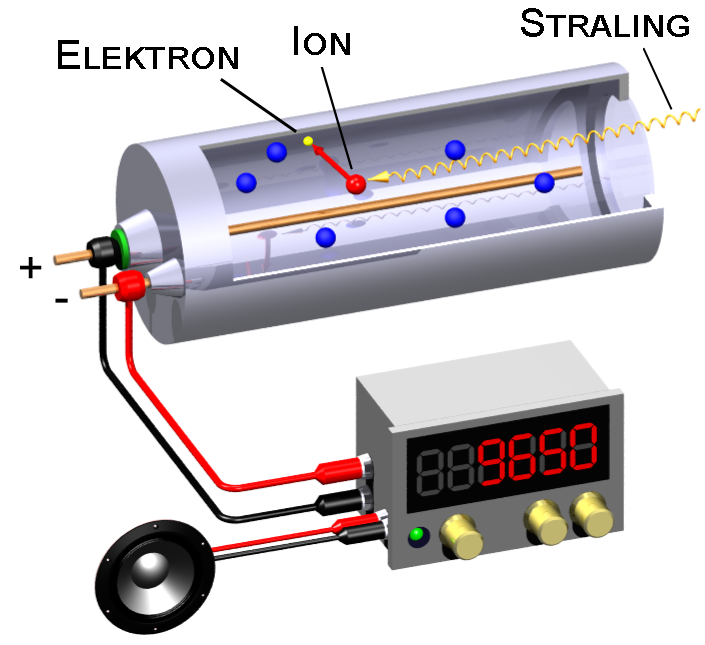(Afbeelding: ... / Svjo-2; CC BY-SA 2.0)
Zelfs als je een geigerteller niet bij een bron houdt, zal je af en toe een piepje horen. Dit komt doordat radioactieve stoffen in kleine hoeveelheden voorkomen in veel voorwerpen om ons heen. We noemen dit de achtergrondstraling. Dit gaat meestal echter maar om een paar piepjes per minuut. Als je de geigerteller echter bij een radioactieve bron houdt, dan hoor je vaak zoveel piepjes dat het niet meer handmatig te tellen is.
FILMPJEMaar wat maakt straling eigenlijk gevaarlijk? Als straling met genoeg bewegingsenergie een atoomkern verlaat, dan kan het andere atomen ioniseren (dit betekent dat er elektronen uit deze atomen getrokken worden). De mate waarin straling in staat is andere atomen te ioniseren noemen we het ioniserend vermogen. Ioniserende straling kan schadelijk zijn voor de gezondheid. Het kan bijvoorbeeld het DNA beschadigen en dit kan het begin zijn van een tumor. Het is dus belangrijk dat we in omgang met radioactieve bronnen goede voorzorgsmaatregelen treffen.
Er zijn twee manieren waarop je schade kan ondervinden van straling. De eerste is bestraling. Bij bestraling bevindt de radioactieve bron zich buiten het lichaam en ondervindt het lichaam schade door de straling die uit deze bron schiet. Als deze deeltjes echter hun impact gemaakt hebben, dan zijn ze verder onschadelijk. Als je dus van de bron wegloopt, dan neemt de schade niet toe. De straling zelf is immers niet radioactief. Bij besmetting komt de radioactieve bron in het lichaam terecht. Het is dus niet mogelijk om van deze bron weg te lopen. Besmetting is daarom over het algemeen gevaarlijker dan bestraling.
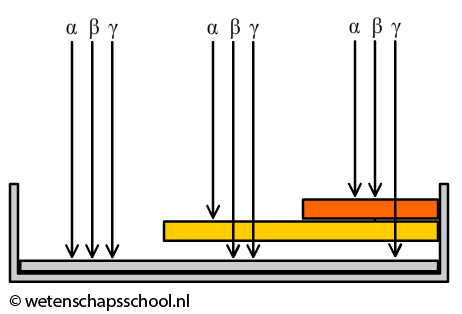
Mensen die werken met radioactieve stoffen dragen vaak een badge. Een badge maakt gebruik van het verschil in doordringend vermogen van de verschillende typen straling. Hoe hoger het doordringend vermogen, hoe gemakkelijker de straling door materialen heendringt. De daadwerkelijke afstand die straling aflegt als het een stof binnendringt, noemen we de dracht. Alfastraling heeft een klein doordringend vermogen en dus ook de kleine dracht. Zelfs door lucht kan alfastraling slechts enkele centimeters voortbewegen. Bètastraling heeft een groter doordringend vermogen en dat van gammastraling is het grootst. In de onderstaande linker afbeelding zien we een doorsnede van de badge. Het linker deel van de badge laat alle soorten straling door. Het middelste deel laat bèta- en gammastraling door en het rechter deel alleen gammastraling. De straling die doorgelaten wordt komt tegen een film aan die verkleurt door straling. Door de verkleuring op de drie plekken te vergelijken, kan je voor elk type straling achterhalen aan hoeveel straling de badge (en dus de persoon) heeft blootgestaan.
In het onderstaande filmpje wordt het verschillend doordringend vermogen van alfa-, beta-, en gammastraling gedemonstreerd:
DEMO:
Doordringend vermogen
Maar naast de gevaren hebben radioactieve stoffen ook veel voordelen. In de eerste paragraaf hebben we gelezen dat we er energie mee kunnen opwekken. In deze paragraaf gaan we leren dat radioactieve stoffen ook veel in het ziekenhuis gebruikt worden om het lichaam in kaart te brengen en zo te achterhalen wat er aan de hand is met een patient.
Een bekende techniek is scintigrafie. Bij deze techniek wordt er een radioactieve stof, genaamd een tracer, in het lichaam gespoten. Deze stof hoopt zich op bepaalde plekken in het lichaam op en zendt hier gammastraling uit. Een deel van deze straling zal het lichaam verlaten, waar het in een detector terecht komt. Met behulp van deze straling kan dan een foto van de binnenkant van het lichaam gemaakt worden.
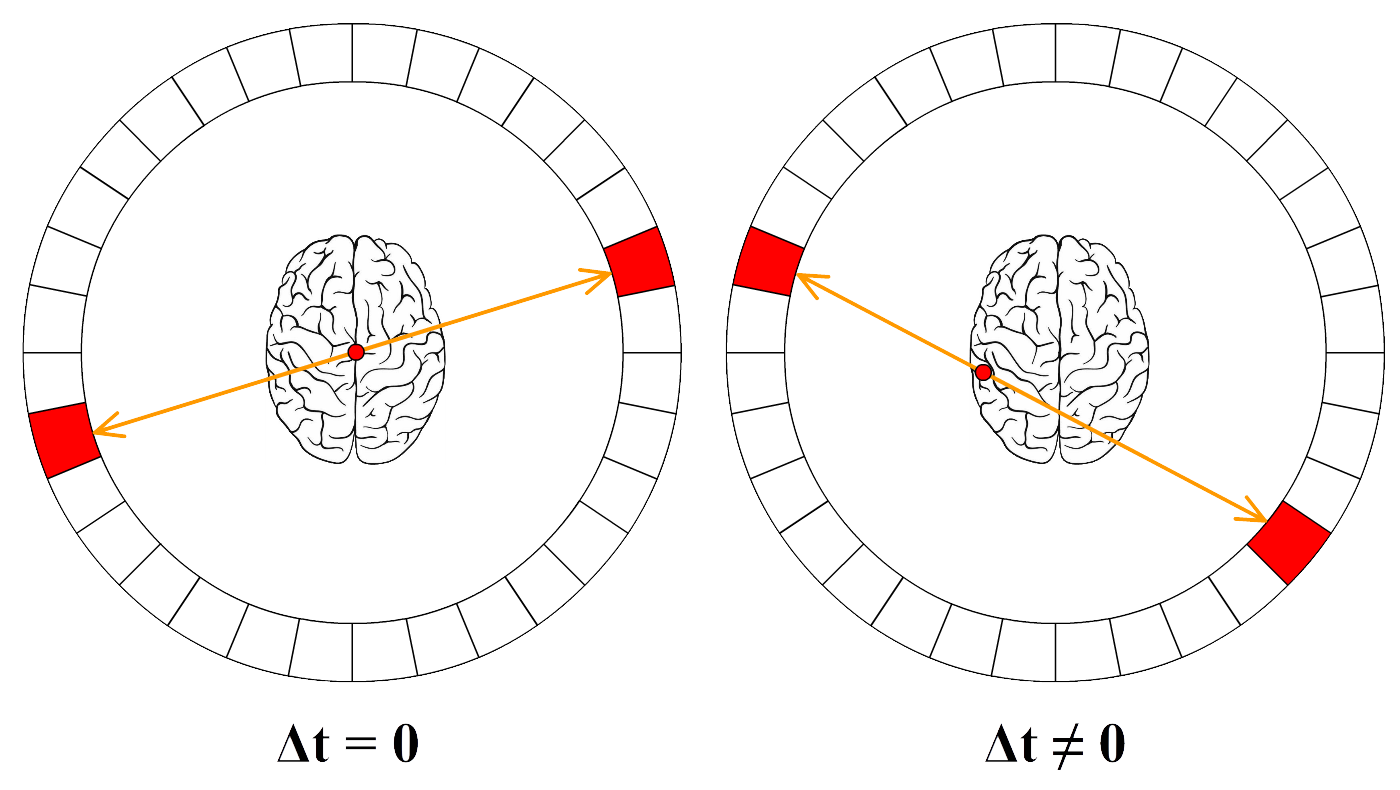
Een bekend voorbeeld hiervan is de PET-scan. Als de radioactieve stof bij een PET-scan vervalt, dan ontstaan twee fotonen die in tegengestelde richting wegschieten. Een deel van deze fotonen zal het lichaam verlaten en worden gedetecteerd door een cirkelvormige detector, zoals in de volgende afbeelding is weergegeven. Deze detector maakt dan een "foto" met behulp van deze straling.
In de onderstaande afbeelding zien we PET-scans van de hersenen. Er is in dit geval als tracer radioactief glucose gebruikt. Hersendelen die meer actief zijn nemen meer glucose op en als gevolg lichten deze delen meer op in de PET-scan. Op deze manier kunnen we dus een idee krijgen van hersenactiviteit. Dezelfde methode kan ook gebruikt worden bij het opsporen van tumoren. Tumoren gebruiken namelijk relatief veel glucose en lichten daarom duidelijk op in de scan. Een ander bekend voorbeeld is het gebruik van een jood-tracer voor het onderzoek naar de schildklier. De schildklier neemt relatief veel jood op en als gevolg maakt dit de schildklier goed zichtbaar met een PET-scan.
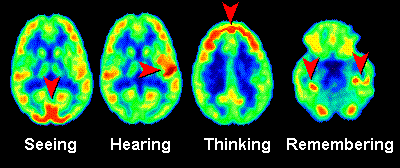(Afbeelding: Phelps & Mazziotta, UCLA)
|
Zorg dat je kan redeneren met de begrippen uit de paragraaf
|
|
