In deze paragraaf gaan we muziekinstrumenten bestuderen. In muziekinstrumenten ontstaan zogenaamde staande golven. In deze paragraaf gaan we deze golven leren beschrijven met tekeningen en formules.
In de onderstaande animatie zie je twee dezelfde golven die in tegengestelde richting bewegen. De individuele golven zijn in het rood en het blauw aangegeven. De superpositie van de twee golven is weergegeven in het zwart. De golf die ontstaat beweegt niet naar links en niet naar rechts en is dus geen lopende golf. We noemen dit type golf een staande golf. Zoals je kunt zien staan sommige punten van het touw de gehele tijd stil. Deze punten noemen we knopen. Andere punten in het touw bewegen maximaal omhoog en naar beneden. We noemen dit buiken.
We zien deze golven bijvoorbeeld als we een gitaarsnaar aanslaan. Hieronder zien we de drie simpelste staande golven die in een gitaarsnaar kunnen ontstaan. De bovenste staande golf wordt de grondtoon (n = 1) genoemd. Zoals je kunt zien heeft deze golf een buik in het midden en twee knopen aan de zijkant. De twee knopen aan de zijkant ontstaan natuurlijk omdat de snaar aan de uiteinden vastzit.
De andere tonen die zijn afgebeeld noemen we de boventonen. Voor de eerste boventoon schrijven we n = 2. Voor de tweede boventoon geldt n = 3. Etc. Je kunt in de bovenstaande animatie zien dat elke opvolgende toon een extra knoop en een extra buik bevat. De grondtoon is meestal dominant en als niet anders vermeld is in de vraag, dan mag je aannemen dat n = 1.
Zoals je kunt zien bevat de snaar in de grondtoon een halve golflengte. De snaar in de eerste boventoon bevat een hele golflengte. De snaar in de tweede boventoon bevat anderhalve golflengte etc. We kunnen dit patroon samenvatten met de volgende formule:
| Lengte trillend voorwerp (L) | meter (m) |
| Nummer toon (n) | 1, 2, 3, ... |
| Golflengte (λ) | meter (m) |
Als we de frequentie van de grondtoon f1 weten, dan kunnen we de daaropvolgende frequenties als volgt vinden:
| Frequentie van grondtoon (f1) | hertz (Hz) |
| Nummer toon (n) | 1, 2, 3, ... |
| Frequentie van toon n (fn) | hertz (Hz) |
In de onderstaande afbeelding zien we de eerste boventoon in een snaar afgebeeld. Je kan zien dat er nu een hele golf in de snaar past. Hieruit kunnen we concluderen dat de afstand van een knoop tot een buik gelijk is aan een kwart golflengte. Het is handig om dit te onthouden.

In de volgende animatie zien we een andere soort staande golf. Aan de linkerkant wordt een touw omhoog en naar beneden bewogen. Aan de rechterkant kan het touw vrij bewegen. Bij dit type staande golf hebben we dus aan beide uiteinden een buik.
Ook in dit geval bestaat de golftoon uit een halve golflengte, de eerste boventoon uit een hele golflengte, etc. Ook hier geldt dus dezelfde formule:
| lengte trillend voorwerp (L) | meter (m) |
| Nummer toon (n) | 1, 2, 3, ... |
| Golflengte (λ) | meter (m) |
Ook hier geldt:
| Frequentie van grondtoon (f1) | hertz (Hz) |
| Nummer toon (n) | 1, 2, 3, ... |
| Frequentie van toon n (fn) | hertz (Hz) |
In het derde geval bewegen we een touw aan het linker uiteinde op en neer en zit het rechter uiteinde vast. In dit geval hebben we aan het linker uiteinde altijd een buik en aan het rechter uiteinde altijd een knoop.
De grondtoon bevat slechts één buik en één knoop. Er zit nu slechts een kwart golf in het touw. Bij de eerste boventoon zien we twee knopen en twee buiken. In dit geval past er dus driekwart van een golf in het touw. Etc. We kunnen dit patroon samenvatten met de volgende formule:
| lengte trillend voorwerp (L) | meter (m) |
| Nummer toon (n) | 1, 2, 3, ... |
| Golflengte (λ) | meter (m) |
In dit geval geldt:
| Frequentie van grondtoon (f1) | hertz (Hz) |
| Nummer toon (n) | 1, 2, 3, ... |
| Frequentie van toon n (fn) | hertz (Hz) |
Ook in lucht kunnen we staande golven creëren. Hieronder zien we een buis die aan twee kanten geopend is. Aan de linker opening van de buis plaatsen we een luidspreker. Aan de uiteinden kan de lucht nu vrij bewegen. Er bevinden hier dus buiken. Bij n = 1 bevindt er in het midden van de buis een knoop. Hier staat de lucht stil. We krijgen hier dus hetzelfde knopen- en buikenpatroon als bij het touw met twee losse uiteinden.
In de onderstaande animatie is één kant van de buis gesloten. Het knopen- en buikenpatroon is hier gelijk aan dat van een touw dat aan één kant vast zit en aan de andere kant vrij beweegt.
Als we in de praktijk een toon produceren met een muziekinstrument, dan horen we meestal een complexe combinatie van de grondtoon en de boventonen. Hieronder zien we bijvoorbeeld het geluidspectrum van een fluit. De eerste piek die we zien is de grondtoon en de rest van de pieken zijn de boventonen. De positie en de hoogte van deze pieken verklaart het verschil tussen het geluid van bijvoorbeeld een fluit, een trompet of een gitaar.
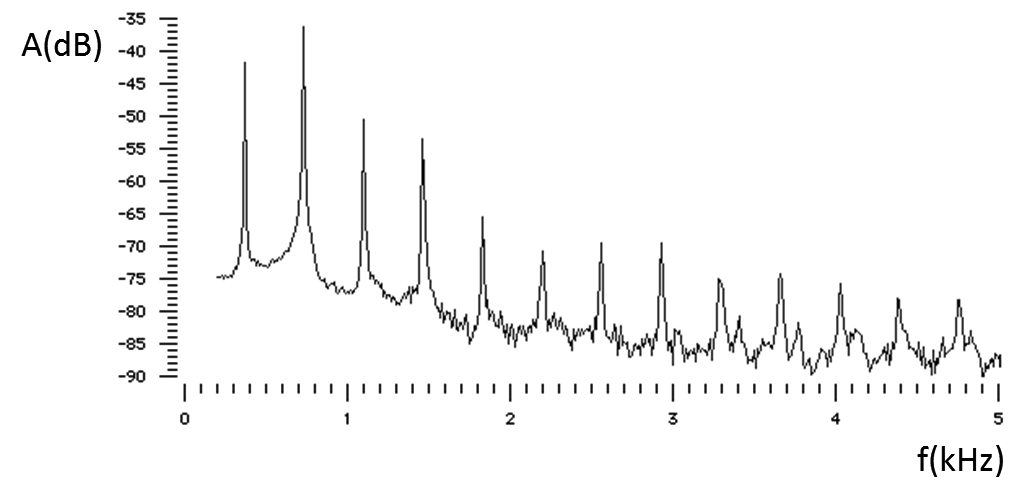
In de bovenstaande grafiek zien de alleen bij bepaalde frequenties de geluidsterkte dramatisch toeneemt. Waar hebben we dit eerder gezien? Dit is resonantie! De pieken zijn dus resonantiepieken en dit verklaart waarom muziekinstrumenten een goed hoorbare toon kunnen voortbrengen.
Bij de harmonische trilling in paragraaf 2 hoort slechts één eigenfrequentie. In dit geval hebben we een hele serie eigenfrequenties die overeenkomen met de grondtoon en de boventonen. In het onderstaande programma zien we hoe een golf en het bijbehorende (u,t)-diagram eruit ziet als een toon in meerdere eigenfrequenties tegelijk gaat trillen. Zoals je ziet levert een combinatie van staande golven meestal geen staande golf op.
- (5) Leg uit hoe groot de afstand is tussen een knoop en een buik, uitgedrukt in de golflengte.
- (5) Teken het patroon van buiken en knopen bij een gitaarsnaar. Doe dit voor de grondtoon en de eerste twee boventonen. Gebruik de letter K om een knoop aan te duiden en de letter B om een buik aan te duiden.
- (5) Teken het patroon van buiken en knopen bij een panfluit met twee open uiteinden. Doe dit voor de grondtoon en de eerste twee boventonen. Gebruik de letter K om een knoop aan te duiden en de letter B om een buik aan te duiden.
- (5) Doe nu hetzelfde voor een panfluit met één open uiteinde en één gesloten uiteinde.
- (5)
Het geluid van een stemvork wordt vaak versterkt door deze op een klankkast te zetten die aan de ene kant gesloten is en aan de andere kant open. Een bepaalde klankkast heeft een lengte van 17,8 cm en de lucht in de klankkast gaat in zijn grondtoon trillen.
- Bereken de frequentie behorende bij deze grondtoon.
- De buik die ontstaat aan het open uiteinde van de klankkast bevindt zich eigenlijk iets buiten de opening. Heeft de stemvork in dat geval een grotere of een kleinere frequentie dan berekend bij vraag a. Licht je antwoord toe.
- (5)
In een mondharmonica zit een rij met gaatjes. Onder elk gaatje zit een metalen lipje van verschillende lengte.
Een lipje is een dun koperen stripje dat aan één kant is vastgemaakt. Het andere uiteinde kan vrij trillen. Het zijaanzicht van een lipje is hieronder weergegeven.
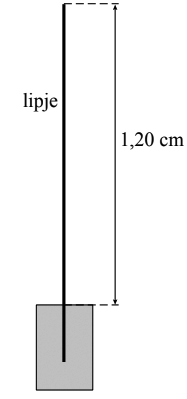 Als een speler lucht door een gaatje blaast, ontstaat in het lipje onder dat gaatje een staande golf. Het lipje trilt dan in de grondtoon.
Als een speler lucht door een gaatje blaast, ontstaat in het lipje onder dat gaatje een staande golf. Het lipje trilt dan in de grondtoon.
- Als het lipje in de grondtoon trilt, ontstaat een toon van 392 Hz. Bereken de voortplantingssnelheid van de golven in het lipje.
- (5V)
Met behulp van een microfoon worden twee geluidsopnames gemaakt waarbij een persoon door twee verschillende gaten blaast. Van deze twee opnames zijn de volgende (u,t)-diagrammen gemaakt:
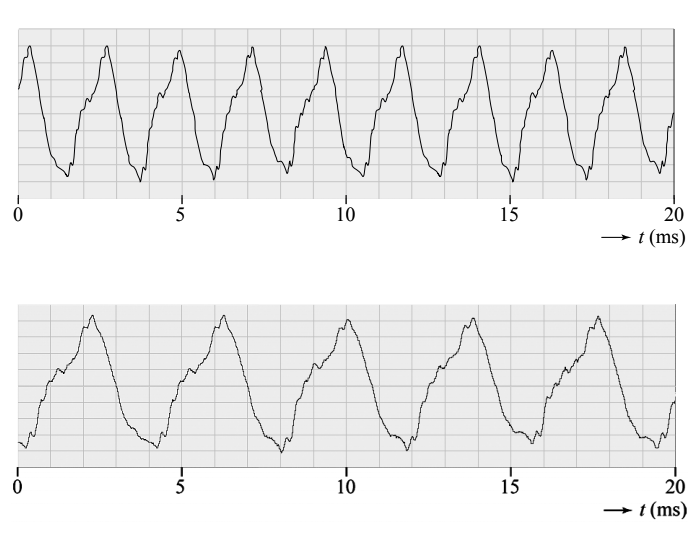 Leg uit welke van deze figuren correspondeert met het langste lipje.
Leg uit welke van deze figuren correspondeert met het langste lipje.
- Naast de grondtoon gaat het lipje (zeker bij hard blazen) ook trillen in de eerste boventoon. Geef in een tekening weer op welke plaatsen zich buiken en knopen bevinden als het lipje in de eerste boventoon trilt.
- (5)
Een leerling maakt zelf een panfluit bestaande uit buizen van verschillende lengte. Als zij over een buis blaast, gaat de lucht in deze buis trillen en ontstaat er geluid.
- Hieronder staan twee zinnen over de geluidsgolven in deze buis. Geef voor elke zin het juiste alternatief: In de buis bevinden zich transversale / longitudinale geluidsgolven met verschillende snelheden / frequenties. Er treedt resonantie op zodra de amplitude / golflengte van een golf in verhouding is met de lengte van de luchtkolom in de buis.
- De buizen waar de panfluit uit bestaat zijn aan beide uiteinden open. Teken de knopen (K) en buiken (B) behorende bij de grondtoon.
- De buizen worden nu aan de onderkant afgesloten met kurken. De buis heeft een lengte van 18,8 cm. De kurk steekt 1,0 cm in de buis. De temperatuur van de lucht is 20 graden Celsius. Bereken de frequentie van de grondtoon die de buis dan laat horen.
- Bij een meting blijkt de frequentie van de grondtoon hoger dan verwacht. Een leerling denkt dat dit komt omdat de luchttemperatuur in de panfluit groter is dan 20 graden Celsius. Kan de hogere temperatuur de oorzaak zijn?
- De leerling kan de frequentie van een buis ook iets aanpassen door de kurk dieper of minder diep in de buis te duwen. Leg uit welke kant de kurk op geduwd moet worden om de grondtoon op een lagere waarde te krijgen.
- (5)
Als alle gaatjes van een blokfluit dichtgehouden worden, dan produceert de blokfluit een toon met een grondfrequentie van 520 Hz. Je mag ervan uitgaan dat aan beide uiteinden van de blokfluit een buik zit.
- Bereken de afstand tussen de twee uiteinden.
- Het middelste gaatje dat precies halverwege de blokfluit zit, wordt nu geopend. Leg uit welke frequentie de blokfluit nu voortbrengt.
- (5V)
Een ukelele is een klein formaat gitaar met vier snaren (zie de onderstaande afbeelding). Alle snaren zijn gemaakt van nylon. Een ukelele kan op verschillende manieren gestemd worden.
 Een manier van stemmen is hieronder weergegeven:
Een manier van stemmen is hieronder weergegeven:
snaar grondtoon f(Hz) 1 G 392 2 C 262 3 E 330 4 A 440 - Laat met behulp van de tabel zien dat de golfsnelheid in de snaren niet gelijk is.
- Als snaar 3 en 4 tegelijk worden aangetokkeld, is er een klank te horen die als prettig ervaren wordt. We zeggen ook wel dat deze twee snaren 'stemmen'. Een verklaring hiervoor is dat deze snaren een of meer gemeenschappelijke boventonen hebben. Bepaal de frequentie van de laagste gemeenschappelijke boventoon van de snaren 3 en 4.
- Het verband tussen de spankracht en de golfsnelheid in een snaar kan worden weergegeven met behulp van: $$ v = \sqrt{\frac{F}{\mu}} \;\;\;\; \text{met } \; \mu =\frac{m}{l} $$ Hierin is v de golfsnelheid en F de spankracht, m de massa en l de lengte van de snaar. Laat met behulp van deze formule en formules uit BINAS zien dat geldt dat: $$ F = \frac{\lambda^2 f^2 \pi d^2 \rho}{4} $$ Hierin is d de dikte van de snaar en ρ de dichtheid van het materiaal van de snaar.
- De dikte van snaar 1 bedraagt 0,65 mm. De ukelele is gestemd op de manier zoals weergegeven in de tabel. Bepaal de spankracht in snaar 1.
- (5)
De spaken van een fiets kunnen door een fietsenmaker worden afgesteld. Door tegen een spaak te tikken kan de fietsenmaker testen of de spaak genoeg gespannen is. Er komt hierbij namelijk een toon vrij, die als volgt afhangt van de spankracht in de spaak:
$$ v = \sqrt{\frac{F_s}{\mu}} $$
μ is hier de massa per lengte eenheid in kg/m.
- De lengte van een spaak is 30 cm en de massa 6,00 g. De fietsenmaker hoort een toon van 300 Hz. Bereken de spankracht in de spaak.
- Leg met behulp van bovenstaande formule uit of de toon die de spaak geeft hoger of lager wordt als de spaak strakker aangedraaid wordt.
- (5V)
Hieronder zien we het spectrum van een bepaald muziekinstrument met een luchtkolom:
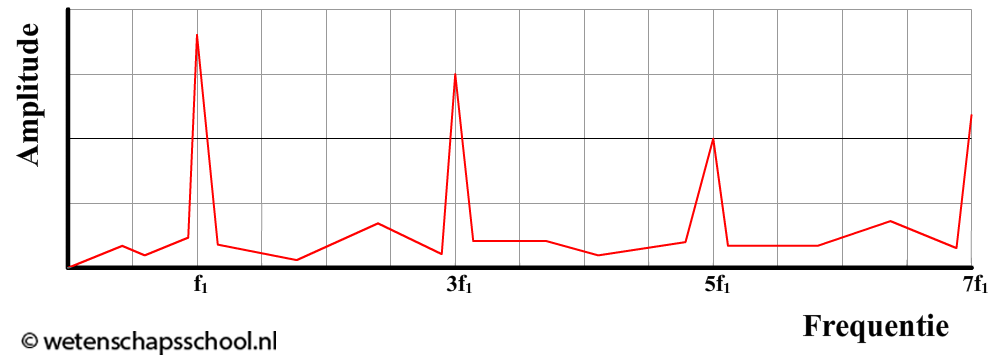 Laat met een berekening zien of we hier te maken hebben met een luchtkolom die aan beide kanten open is of dat één kant gesloten is.
Laat met een berekening zien of we hier te maken hebben met een luchtkolom die aan beide kanten open is of dat één kant gesloten is.
- (5)
Een vleugel is een muziekinstrument met toetsen en snaren. Als een toets wordt ingedrukt slaat een houten hamertje tegen een strak gespannen snaar die vervolgens gaat trillen. De klank die je hoort, bestaat uit de grondtoon en enkele boventonen.
- Afhankelijk van de plek waar het hamertje de snaar raakt, zullen de verschillende boventonen wel of niet meeklinken. Stel dat het hamertje neerkomt op 1/8ste deel van de lengte van de snaar. De boventoon die op deze plek een knoop heeft, klinkt dan niet mee. Noem de laagste boventoon waarbij dit gebeurt.
- Niet alle snaren in een vleugel zijn even lang. De snaar die de hoogste toon voortbrengt heeft een lengte van 40 cm. De hoogste toon van de vleugel heeft een grondfrequentie van 4186 Hz. De laagste toon heeft een grondfrequentie van 32,70 Hz. Veronderstel dat alle snaren even strak gespannen zijn, even dik zijn en van hetzelfde materiaal gemaakt zijn. Toon met een berekening aan dat de lengte die de langste snaar dan zou moeten hebben niet in een vleugel past.
- De toonhoogte van een snaar hangt, behalve van de lengte, ook af van de spankracht in de snaar. Voor de voortplantingssnelheid v van de golven in de snaar geldt: $$ v = \sqrt{\frac{F_s l}{m}} $$ Om ervoor te zorgen dat de snaren die de lage tonen moeten voortbrengen toch in de vleugel passen, kun je verschillende maatregelen nemen. Helpt het om de snaar strakker te spannen?
- En helpt het als we roestvrijstalen snaren vervangen door koperen snaren? Leg je antwoord uit.
- (5)
Het oor bestaat uit drie gedeeltes: het buitenoor, het middenoor en het binnenoor. Het buitenoor is op te vatten als een buis die aan één kant gesloten is door het trommelvlies.
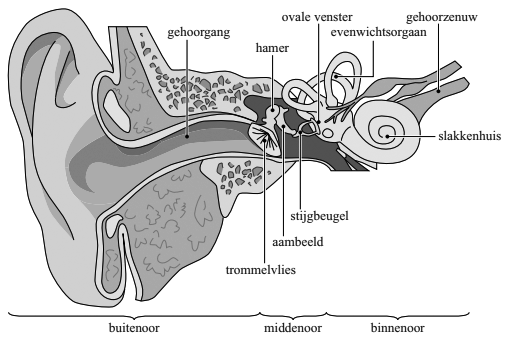
- De gehoorgang is bij een volwassen persoon 28 mm lang. Door resonantie wordt geluid met een frequentie van 3 kHz in het buitenoor versterkt. Toon dat aan met behulp van een berekening.
- Leg uit of de frequentie waarbij versterking optreedt bij een baby groter of kleiner is dan bij een volwassen persoon.
-
In het binnenoor zit het slakkenhuis. Hieronder is een tekening gemaakt van het slakkenhuis in uitgerolde toestand. Het is te beschouwen als een met vloeistof gevulde buis met het basilaire membraan als scheidingswand. Op het basilaire membraan zitten kleine massa's, die allemaal een andere eigenfrequentie hebben.
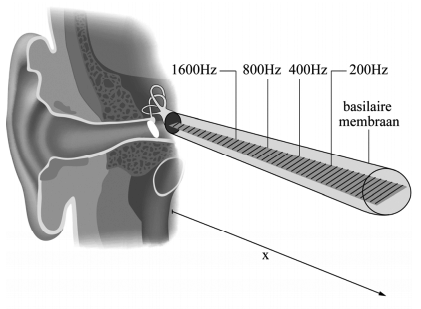 Als het ovale venster in trilling gebracht wordt, ontstaat in de vloeistof rondom het basilaire membraan een druktrilling. Leg uit dat bij verschillende tonen, verschillende massa's flink gaan trillen.
Als het ovale venster in trilling gebracht wordt, ontstaat in de vloeistof rondom het basilaire membraan een druktrilling. Leg uit dat bij verschillende tonen, verschillende massa's flink gaan trillen.
- De stijfheid van het basilaire membraan is vergelijkbaar met de veerconstante C van een massaveersysteem. De stijfheid van het basilaire membraan verandert met de afstand x tot het ovale venster. Dit is duidelijk te zien in de onderstaande afbeelding:
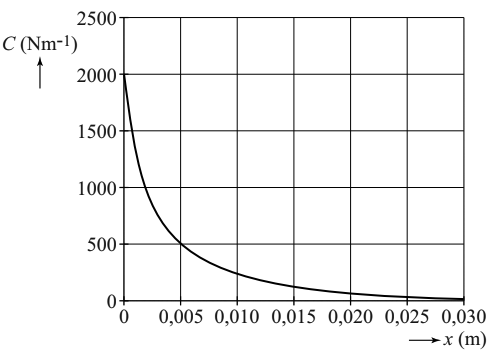 Op een afstand van 5,0 mm van het ovale venster bedraagt de eigenfrequentie 3,0 kHz.
Bepaal de massa in het gebruikte model op die plaats van het basilaire membraan.
Op een afstand van 5,0 mm van het ovale venster bedraagt de eigenfrequentie 3,0 kHz.
Bepaal de massa in het gebruikte model op die plaats van het basilaire membraan.
- In de tweede afbeelding is te zien dat de frequentie 4 keer kleiner wordt als de afstand (x) verdubbeld. Ga na met welke factor de massa's toenemen bij deze verdubbeling van afstand.
- (5)
Op sommige plekken op aarde is het verschil tussen eb en vloed zeer groot. De plaats Saint John aan de Fundybaai in Canada is zo'n plaats. De 300 km lange Fundybaai waaraan Saint John ligt, is hieronder weergegeven:
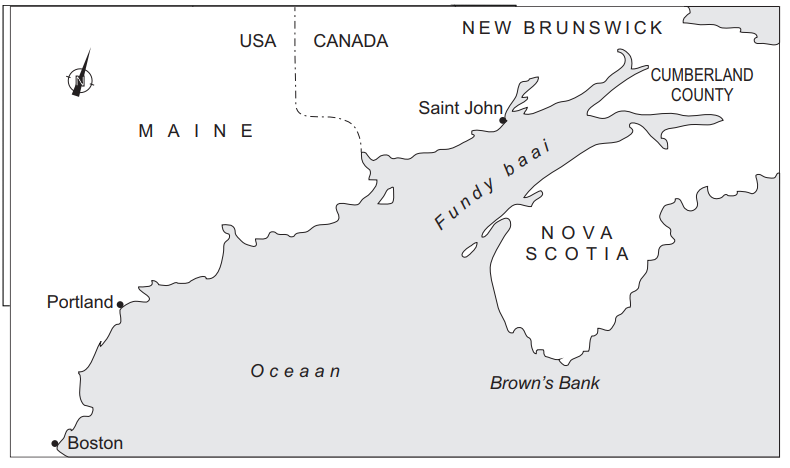 Door zijn vorm en afmetingen ontstaat in de Fundybaai een staande golf. Hieronder is het zijaanzicht van deze golf op drie momenten schematisch weergegeven.
Door zijn vorm en afmetingen ontstaat in de Fundybaai een staande golf. Hieronder is het zijaanzicht van deze golf op drie momenten schematisch weergegeven.

- Elke 12 uur is het 1x eb en 1x vloed. Bereken op basis van o.a. dit gegeven de golfsnelheid.
-
Het verschijnsel dat optreedt in de Fundybaai heet 'getijdenresonantie'. Dit verschijnsel treedt op meerdere plaatsen op aarde op. Hieronder zien we de versterkingsfactor van de getijdewerking bij baaien van verschillende lengte L.
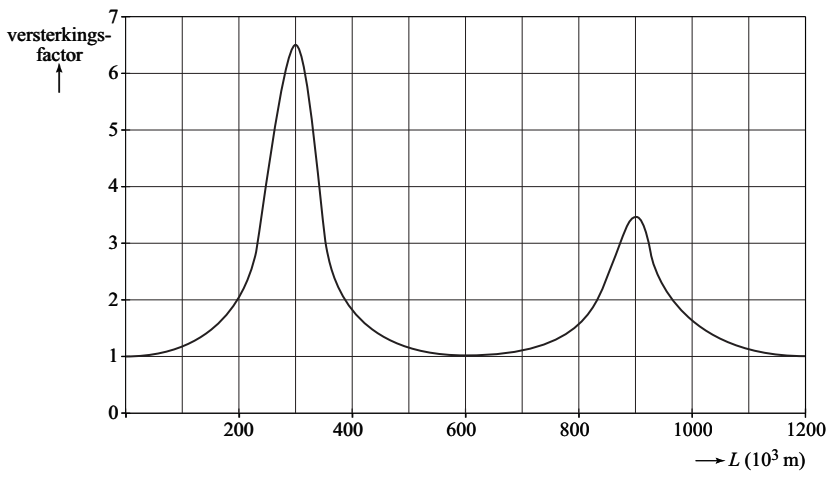 Verklaar dat bij een baailengte van 900 km de versterkingsfactor ook hoog is.
Verklaar dat bij een baailengte van 900 km de versterkingsfactor ook hoog is.