In deze paragraaf gaan we een veelvoorkomende soort trilling bestuderen, de zogenaamde harmonische trilling.
Een simpel systeem dat een harmonische trilling maakt hebben we al gezien, het zogenaamde massa-veersysteem. In het onderstaande (u,t)-diagram is een harmonische trilling weergegeven:
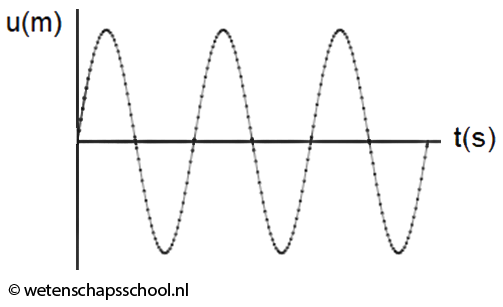
Met behulp van de tweede wet van Newton kan je ook aantonen dat voor elke harmonische trilling geldt dat:
$$ T = 2\pi \sqrt{\frac{m}{C}}$$
| Trillingstijd (T) | seconde (s) |
| Massa (m) | kilogram (kg) |
| Veerconstante (C) | newton per meter (N/m) |
4VWO
Voor elke harmonische trilling geldt ook dat:
$$ F_{res} = -Cu$$
Voor het massa-veersysteem is de resulterende kracht is deze formule gelijk aan de veerkracht. De constante C noemen we bij het massaveersysteem de veerconstante.
De 'min' in de formule zorgt ervoor dat de kracht automatisch in de juiste richting wijst. Als het blokje zich links van de evenwichtstand bevindt (u < 0), dan werkt de veerkracht naar rechts (F > 0). Als het blokje zich rechts van de evenwichtstand bevindt (u > 0), dan werkt de veerkracht naar links (F < 0). Als we met deze formule een model maken, dan vinden we de volgende trilling:
Zoals je kunt zien, vinden ontstaat er een (u,t)-diagram met een sinusvormige grafiek. De formule die bij deze grafiek hoort, wordt gegeven door:
| Resulterende kracht (Fres) | newton (N) |
| Constante (C) | newton per meter (N/m) |
| Uitwijking (u) | meter (m) |
$$ u = A \sin{\left(2\pi \frac{t}{T}\right)} \;\;\;\; \textbf{(radialen)} $$
Let erop dat je bij gebruik van deze formule de rekenmachine op radialen zet.
| Uitwijking (u) | meter (m) |
| Amplitude (A) | meter (m) |
| Tijd (t) | seconde (s) |
| Trillingstijd (T) | seconde (s) |
4VWO
Als laatste kijken we naar de energieomzetting bij een harmonische trilling. Tijdens de beweging zet het blokje telkens veerenergie (1/2Cu2) om in kinetische energie (1/2mv2) en andersom. Aan de uiteinden van de beweging is de snelheid nul. De kinetische energie is hier dus ook nul. Er is hier echter wel een veerenergie. Omdat de uitwijking hier gelijk is aan de amplitude, vinden we dat de totale energie aan de uiteinden gelijk is aan:
$$ E_{tot} = \frac{1}{2}CA^2 \;\;\;\;\;\;\; \text{(uiteinden)}$$
In de evenwichtstand is de uitwijking nul. Er is hier dus geen veerenergie. De snelheid is hier maximaal en als gevolg hebben we hier wel een kinetische energie. In de evenwichtsstand is de totale energie dus gelijk aan:
$$ E_{tot} = \frac{1}{2}mv_{max}^2 \;\;\;\;\;\;\; \text{(evenwicht)} $$
In een van de filmpjes aan het eind van de paragraaf laten we zien dat je hiermee de volgende formule kan afleiden:
$$ v_{max} = \frac{2\pi A}{T} $$
| Maximale snelheid (vmax) | meter per seconde (m/s) |
| Amplitude (A) | meter (m) |
| Trillingstijd (T) | seconde (s) |
Training
- (5)
Marloes heeft een wieg gekocht voor haar baby. De wieg hangt aan een veer en kan zachtjes op en neer trillen. De veerconstante is 1,3 kN/m en de massa van de wieg is 12,2 kg.
- Bereken hoe ver de veer is uitgerekt als de wieg stil aan de veer hangt.
- Marloes legt haar baby van 3,2 kg in de wieg. Als zij de wieg een klein beetje naar beneden duwt en dan loslaat, gaat de wieg met de baby erin een trilling uitvoeren. Bereken de frequentie van deze trilling.
- Marloes heeft gelezen dat baby's gemakkelijker in slaap vallen als de frequentie van het trillen kleiner is. Noem twee aanpassingen aan de wieg die Marloes zou kunnen doen om de frequentie van de wieg kleiner te maken. Licht je antwoord toe.
- (5)
In de onderstaande afbeelding is een speeldoosje weergegeven. Via een hendel en een tandwielconstructie kan een rol in beweging worden gebracht. Op deze rol zijn puntjes aangebracht die de uiteinden van de metalen strips optillen en loslaten.
De hendel van het speeldoosje kan langzamer of sneller worden rondgedraaid. Als de hendel langzamer wordt rondgedraaid, dan worden de stripjes langzamer gebogen door de metalen pennetjes op de rol.
Leg uit of de toonhoogte van de melodie lager wordt, gelijk blijft of hoger wordt, als de hendel sneller wordt rondgedraaid.
(bron: examen VWO 2017-2)
- (5)
In het molecuul waterstofjodide (HI) is een klein waterstofatoom gebonden aan een groter jodiumatoom. De evenwichtsafstand tussen de twee atomen is 1,609 x 10-10 m. Als deze afstand groter of kleiner wordt, zorgt de binding voor een terugdrijvende kracht die in eerste benadering zorgt voor een harmonische trilling.
- De trillingsfrequentie van dit massa-veersysteem is 6,92 x 1013 Hz. Bereken hiermee de veerconstante van deze trilling.
- (VWO) Bij een bepaalde temperatuur bedraagt de trillingsenergie van het waterstofatoom 6,0 x 10-20 J. Bereken hiermee de maximum snelheid van het waterstofatoom.
- (VWO) Bereken de maximale afstand tussen de atomen tijdens het trillen.
- (VWO) Het waterstofatoom bevindt zich vaker rond de maximale uitwijkingen van de beweging dan rond de evenwichtsstand. Leg uit hoe dit komt.
- (5) (VWO) Een persoon test verschillende type veren in een massaveersysteem. Telkens wordt hetzelfde blokje gebruikt. Laat zien dat voor dit massaveersysteem geldt dat: $$ f^2 = c \times C $$ Hier geldt dat C de veerconstante van het systeem is en c een andere constante.
- (5V)
In de onderstaande tabel zijn meetgegevens te zien van een massaveersysteem, waarbij te trillingstijd is gemeten voor blokjes met een verschillende massa.
Maak een gelineariseerde grafiek van deze gegevens en bereken hiermee de veerconstante C.Massa (g) Trillingstijd (s) 10 0,11 20 0,16 30 0,20 40 0,23 50 0,26 60 0,28 70 0,30
Rekenen met de formules voor de harmonische trilling