In deze paragraaf stappen we over van het reguliere (x,t)-diagram uit het hoofdstuk beweging naar het ruimtetijd-diagram. Dit is een type diagram waarbij rekening gehouden wordt met tijddilatatie en lengtecontractie. Het grootste gedeelte van de paragraaf zullen we bezig zijn met het construeren van zo'n diagram. We eindigen met een aantal voorbeelden van hoe we dit diagram aflezen.
In de vorige twee paragrafen hebben we formules gevonden voor de tijddilatatie en de lengtecontractie. We kunnen deze effecten behalve met formules ook weergeven in diagrammen. We noemen dit ruimtetijd-diagrammen, met op de horizontale as de afstand (x(m)) en op de verticale as de tijd vermenigvuldigd met de lichtsnelheid (ct(m)). De eenheid van ct is:
$$ [c][t] = m/s\times s = m $$Het voordeel van dit type diagram is dat voorwerpen die met de lichtsnelheid gaan nu altijd een hoek van 45 graden maken met de x-as. Een voorbeeld hiervan zien we in de onderstaande afbeelding. Om aan te tonen dat het beschreven voorwerp met de lichtsnelheid gaat, gebruiken we de formule voor de snelheid:
$$ v = \frac{\Delta x}{\Delta t} $$Als we nu de teller en de noemer met c vermenigvuldigen, dan vinden we:
$$ v = \frac{c\Delta x}{c\Delta t} $$Als we de c in de teller rechts van de breuk zetten, dan wordt dit:
$$ v = \frac{\Delta x}{c\Delta t} c $$In het onderstaande voorbeeld lezen we af dat x = 5m en ct = 5m. Als we dit invullen in de bovenstaande formule, dan vinden we:
$$ v = \frac{5}{5}c = c $$We hebben hier dus inderdaad te maken met de lichtsnelheid.
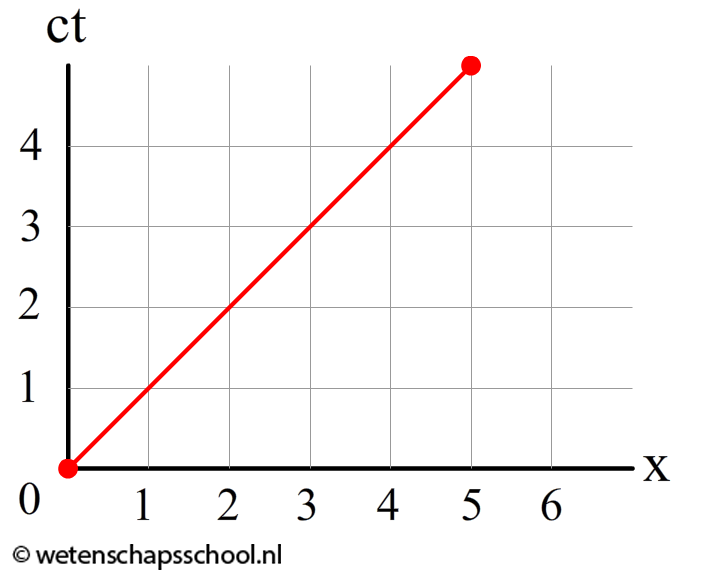
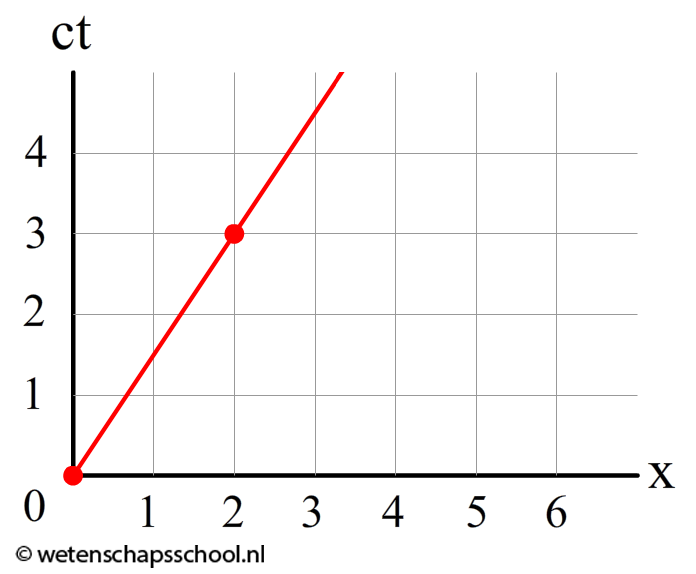
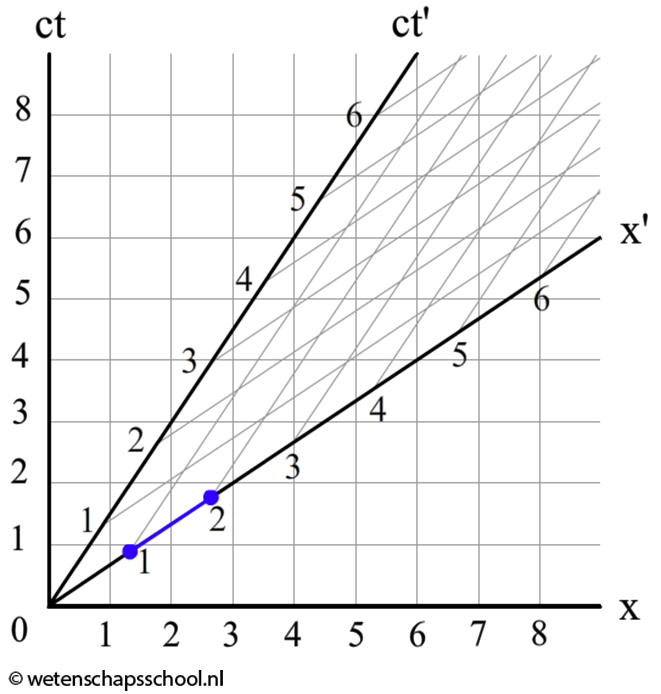
Laten we nog een voorbeeld nemen. Het voorwerp dat in het onderstaande diagram beschreven is heeft de volgende snelheid:
$$ v = \frac{\Delta x}{c\Delta t} c $$ $$ v = \frac{2}{3}c = 0,67 c $$Dit voorwerp beweegt dus met 67% van de lichtsnelheid.
Nu wordt het tijd om weer verschillende stelsels met elkaar te vergelijken. Wederom gaan we eerst bestuderen hoe dit werkt volgens de natuurkunde van Galileo. In de linker onderstaande diagram zien we een waarnemer A die stil staat. We zien dat deze waarnemer stil staat omdat zijn positie (x) hetzelfde blijft als de tijd (ct) voorbij gaat. In het diagram zien we ook een waarnemer in een ruimteschip B dat naar rechts beweegt met 0,67c.
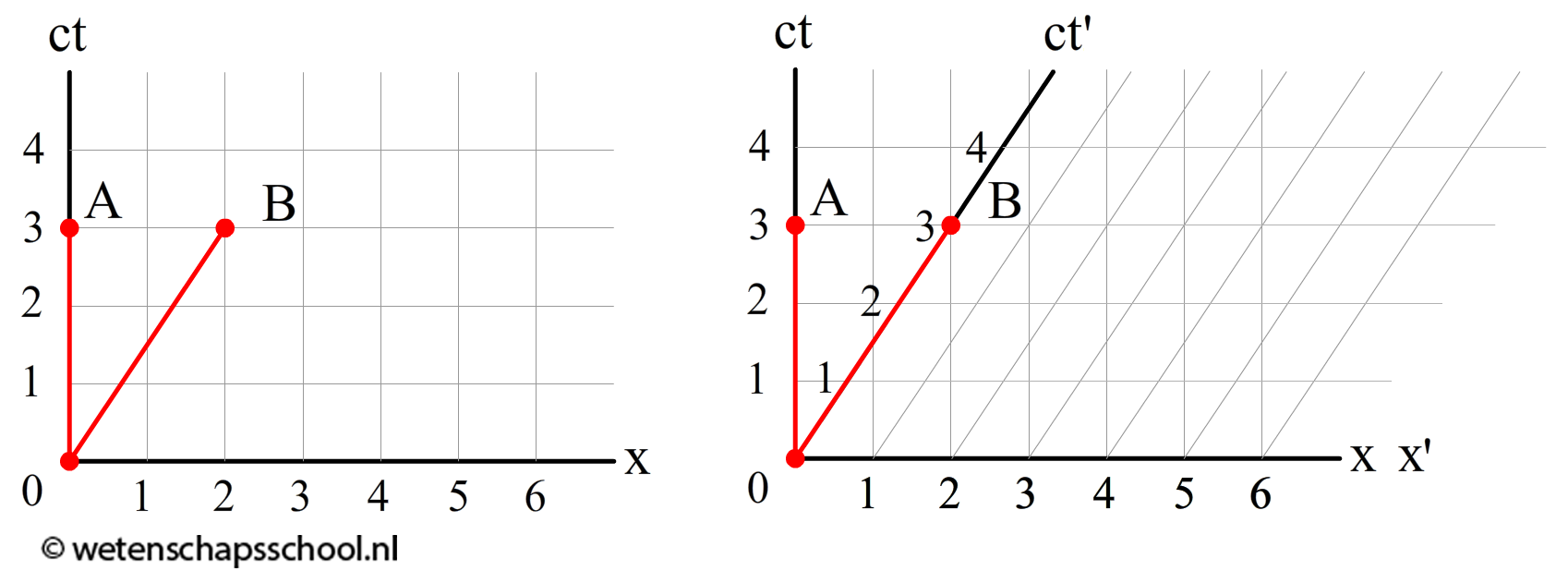
We hadden echter net zo goed aan kunnen nemen dat juist persoon B stil stond. In de bovenstaande afbeelding zien we het diagram volgens persoon B afgebeeld. Om onderscheid te maken tussen de twee diagrammen gebruiken we hier ct' en x'. In dit diagram lijkt het juist alsof waarnemer B stil staat. Zijn positie (x') blijft namelijk hetzelfde als de tijd (ct') voorbij gaat.
Nu passen we de correctie van Einsteins speciale relativiteitstheorie toe. Omdat waarnemer B zich met snelheid 0,67c van waarnemer A af beweegt, vinden we een γ-factor van:
$$ \gamma = \frac{1}{\sqrt{1-\frac{(2/3c)^2}{c^2}}} = \frac{1}{\sqrt{1-(2/3)^2}} = 1,34 $$Stel dat de persoon in het schip elke seconde in zijn handen klapt. Volgens de formule \( \Delta t = \gamma \Delta t_{eigen} \) meet de persoon op aarde tussen de klappen een tijdsduur van 1,34 s. Om dit aan het diagram toe te voegen moeten we de ct'-as dus oprekken (zie de onderstaande diagram). Merk op dat als er 1,00 seconde voorbij is gegaan in het schip, er inderdaad 1,34 s voorbij is gegaan.
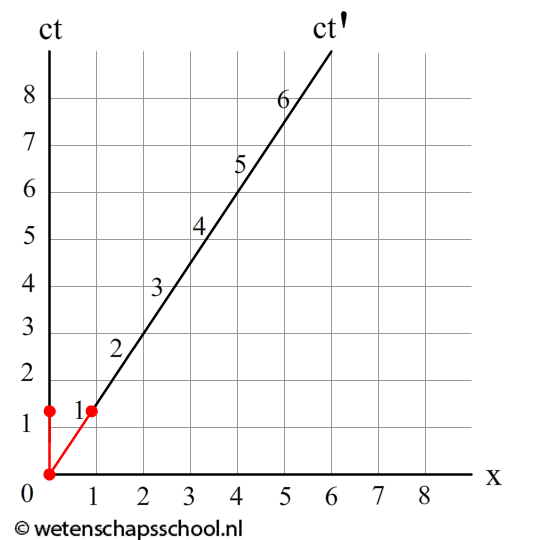
We zijn hiermee echter nog niet klaar. Om het diagram compleet te maken, voeren we het volgende gedachtenexperiment uit. Een persoon in het schip schiet op tijdstip ct' = -3, -2 en -1 een lichtstraal af naar rechts (zie het linker onderstaande diagram). Wederom worden de lichtstralen gekenmerkt door de hoek van 45 graden met de x-as. Op tijdstip ct' = 0 reflecteert de persoon de lichtstralen, waarna ze weer terug naar links gaan. Zoals je ziet vindt de persoon in het schip dat de lichtstralen zijn gereflecteerd op dat x'-as op afstand 1, 2 en 3 meter.
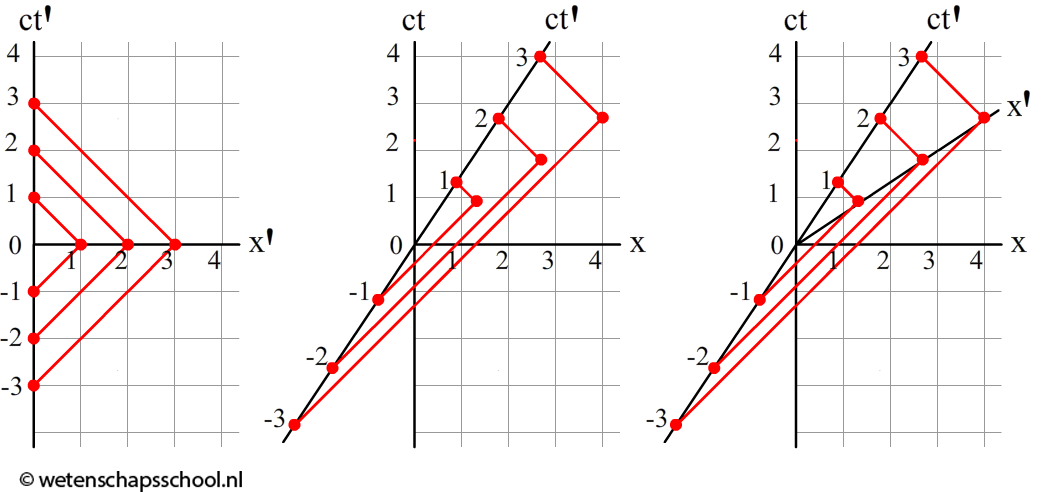
In het middelste diagram zien we dezelfde situatie gezien vanaf de aarde. Wederom starten de lichtstralen op ct'=-3, -2 en -1 en komen de lichtstralen terug op tijdstip ct'=1, 2 en 3 (zie de middelste afbeelding). Omdat we wederom de lichtstralen onder een hoek van 45 graden moeten tekenen, zien we dat de lichtstralen nu op onverwachte plekken reflecteren. We hadden al gezien dat deze punten op de x'-as lagen. Vanaf de aarde gezien staat dus ook de hele x'-as scheef (zie de rechter afbeelding). In de onderstaande afbeelding zien we het uiteindelijke ruimtetijd-diagram. We noemen dit ook wel een Minkowski-diagram:
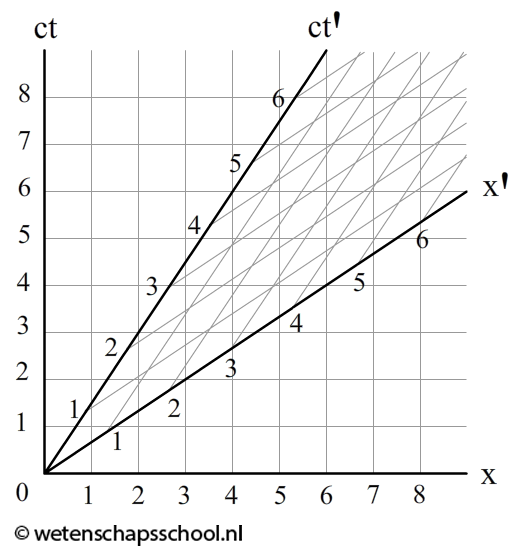
In het onderstaande programma zien we hoe het Minkowski-diagram verandert bij verschillende snelheden. Merk op dat de hoek tussen de ct- en de ct'-as altijd even groot is als de hoek tussen de x- en de x'-as.
Laten we nu oefenen moet het aflezen van Minkowski-diagrammen. In de onderstaande afbeelding zien we een zevental gebeurtenissen die zijn aangegeven met rode punten. Volgens de persoon op aarde (x,ct) vinden deze gebeurtenissen zich achter elkaar plaats. Het linker punt gebeurt eerst en het meest rechtse punt op het laatst. In het bewegende systeem gebeuren al deze gebeurtenissen echter tegelijk! Al deze gebeurtenissen gebeuren namelijk op tijdstip ct' = 0. Dit is wederom de relativiteit van gelijktijdigheid.
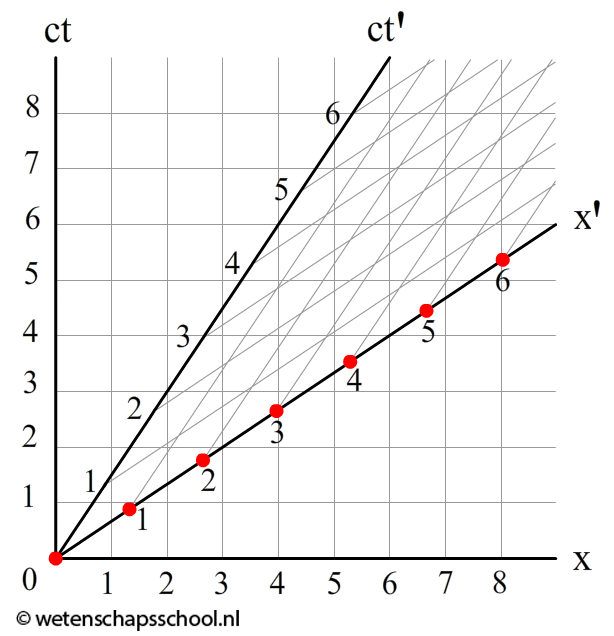
Ook lengtecontractie kunnen we uit het Minkowski-diagram aflezen. Hieronder zien we een voorwerp van 2,0m lang dat stil ligt op aarde (de rode balk). Als we de lengte meten in het (x,ct)-stelsel, dan zien we dat de stok inderdaad 2,0m is. In het bewegende stelsel is de afstand echter gelijk is aan 1,5m! Precies wat we volgens de formule van de lengtecontractie zouden verwachten:
$$ L = \frac{L_{eigen}}{\gamma} $$ $$ L = \frac{2}{1,34} = 1,5 \text{ m} $$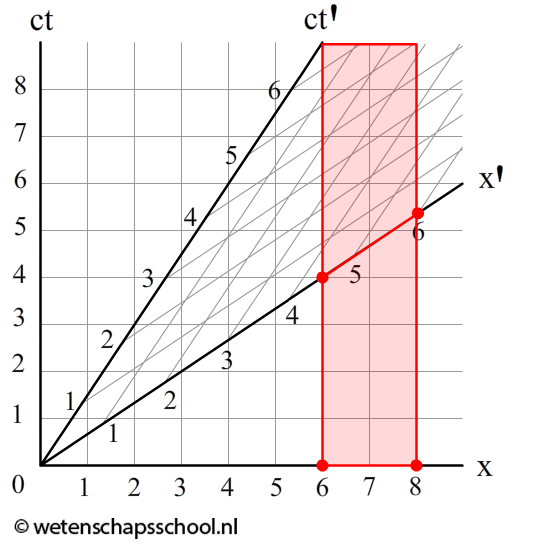
- Teken in een (ct,x)-diagram een grafiek van een ruimteschip dat met een snelheid van 1,0c vanaf de oorsprong naar rechts beweegt.
- Teken in hetzelfde diagram een grafiek van een ruimteschip dat met een snelheid van 2/3c vanaf de oorsprong naar rechts beweegt.
- Teken in hetzelfde diagram een grafiek van een ruimteschip die stil staat.
- Construeer een minkowski-diagram voor een referentiestelsel dat met een snelheid van 4/5c naar rechts beweegt. Bereken hiervoor o.a. met de tijddilatatieformule hoe groot de stappen op de ct'- en x'-as worden.
-
In het onderstaande Minkowski-diagram worden met twee stippen twee gebeurtenissen weergegeven.
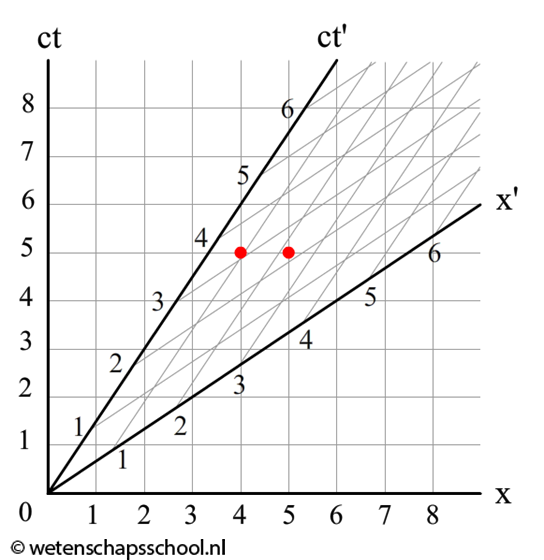
- Leg uit op welk moment de gebeurtenissen plaatsvinden in het stilstaande stelsel. Vinden de gebeurtenissen gelijktijdig plaats?
- Leg uit op welk moment de gebeurtenissen plaatsvinden in het bewegende stelsel. Vinden de gebeurtenissen gelijktijdig plaats?
-
Een persoon maakt een ruimtereis. Zijn raket beweegt mee met het onderstaande bewegende stelsel:
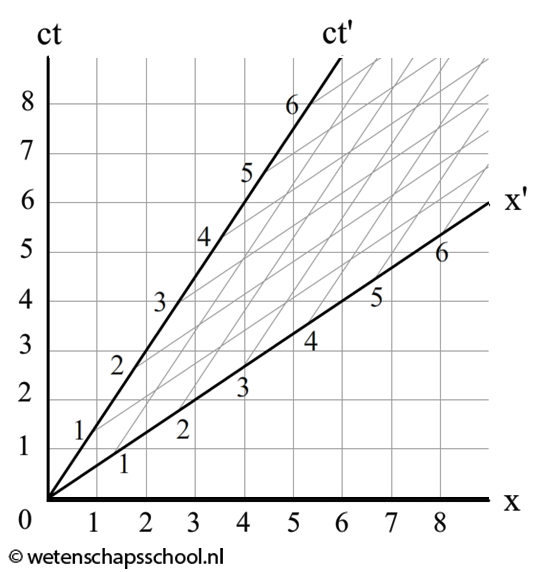
- Een persoon op aarde meet dat de ruimtereis 8 jaar geduurt heeft. Lees met behulp van het diagram af hoeveel tijd er volgens de persoon op aarde voorbij is gegaan in het ruimteschip.
- De persoon in het ruimteschip meet dat de ruimtereis 6 jaar geduurt heeft. Lees met behulp van het diagram af hoeveel tijd er volgens de persoon in het ruimteschip voorbij is gegaan op aarde.
- Laat zien dat je hetzelfde antwoorden bij a) en b) als je niet afleest uit de grafiek, maar de tijddilatatieformule gebruikt.
-
In het stilstaande stelsel ziet een persoon een voorwerp sneller dan het licht van zich af bewegen. Volgens Einstein is dit niet mogelijk. Vanuit een bewegend stelsel gezien kan dit namelijk voor problemen zorgen. Welk probleem merk je hier op? (zie de onderstaande afbeelding).
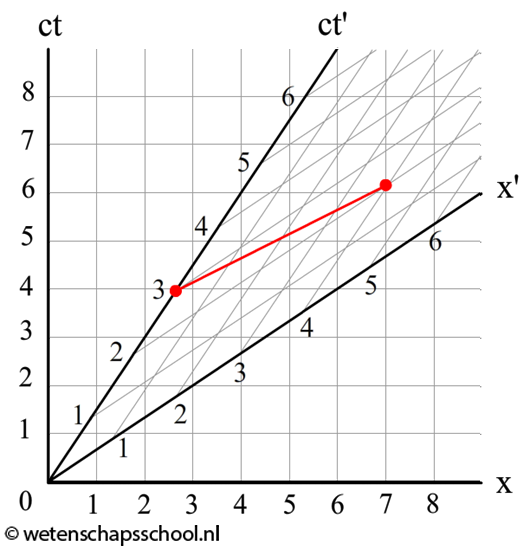
-
In de volgende afbeelding zien we een stok van lengte 1 m die stil staat in het stilstaande stelsel. Gebruik de grafiek om de lengte van de stok in het bewegende stelsel te vinden. (zie de onderstaande afbeelding).
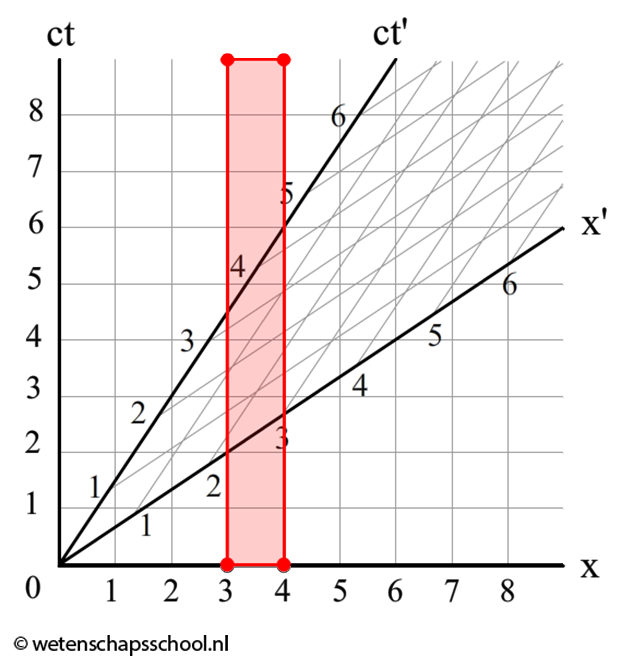
-
Een stok van 1,0 m ligt in het bewegende stelsel (zie de onderstaande afbeelding).
- Ga met behulp van diagram 5 na dat de stok volgens een waarnemer op aarde 0,75 m is.
- Vind hetzelfde resultaat met behulp van de lengtecontractieformule.
 Maken en aflezen van Minkowskidiagrammen
Maken en aflezen van Minkowskidiagrammen