In deze paragraaf gaan we rekenen met de tweede wet van Newton. Deze wet vertelt ons hoe groot de resulterende kracht is werkend op een versnellend voorwerp.

De tweede wet van Newton vertelt ons wat er gebeurt als de resulterende kracht niet nul is. In dat geval geldt:

$$ F_{res} = ma $$
Versnelling (a) meter per seconde per seconden (m/s2)
Resulterende kracht (Fres) newton (N)
Massa (m) kilogram (kg)

De formule wordt ook vaak in de volgende vorm geschreven:

$$ a = \frac{F_{res}}{m} $$

In deze vorm is goed te zien dat een voorwerp versnelt als er een resulterende kracht op werkt. Ook zien we dat deze versnelling kleiner wordt als de massa van het voorwerp groter is. Voorwerpen met een grote massa zijn dus moeilijk in beweging te krijgen en ook moeilijk af te remmen. Hoe groter de massa van een voorwerp is, hoe moeilijker het dus is om de snelheid van dit voorwerp te veranderen. We noemen dit principe traagheid.

Laten we de tweede wet eens toepassen. Hieronder zien we een (v,t)-diagram van een auto met een massa van 2000 kg.

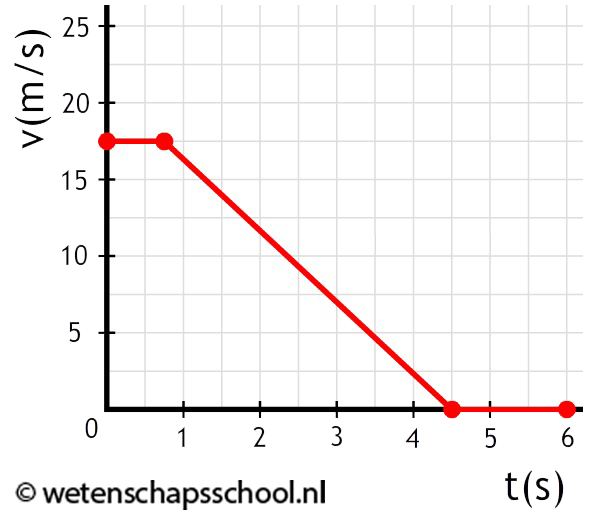
Tijdens het remmen zien we de snelheid afnemen van 17,5 m/s naar 0,00 m/s in 3,75 seconden. De versnelling gedurende het remmen is dan:

$$ a = \frac{\Delta v}{\Delta t} $$ $$ a = \frac{17,5}{3,75} = 4,67 \text{ m/s}^2$$

De resulterende kracht die op de auto werkte tijdens het remmen is dan:

$$ F_{res} = ma $$ $$ F_{res} = 2000 \times 4,67 = 9,34 \times 10^3 \text{ N} $$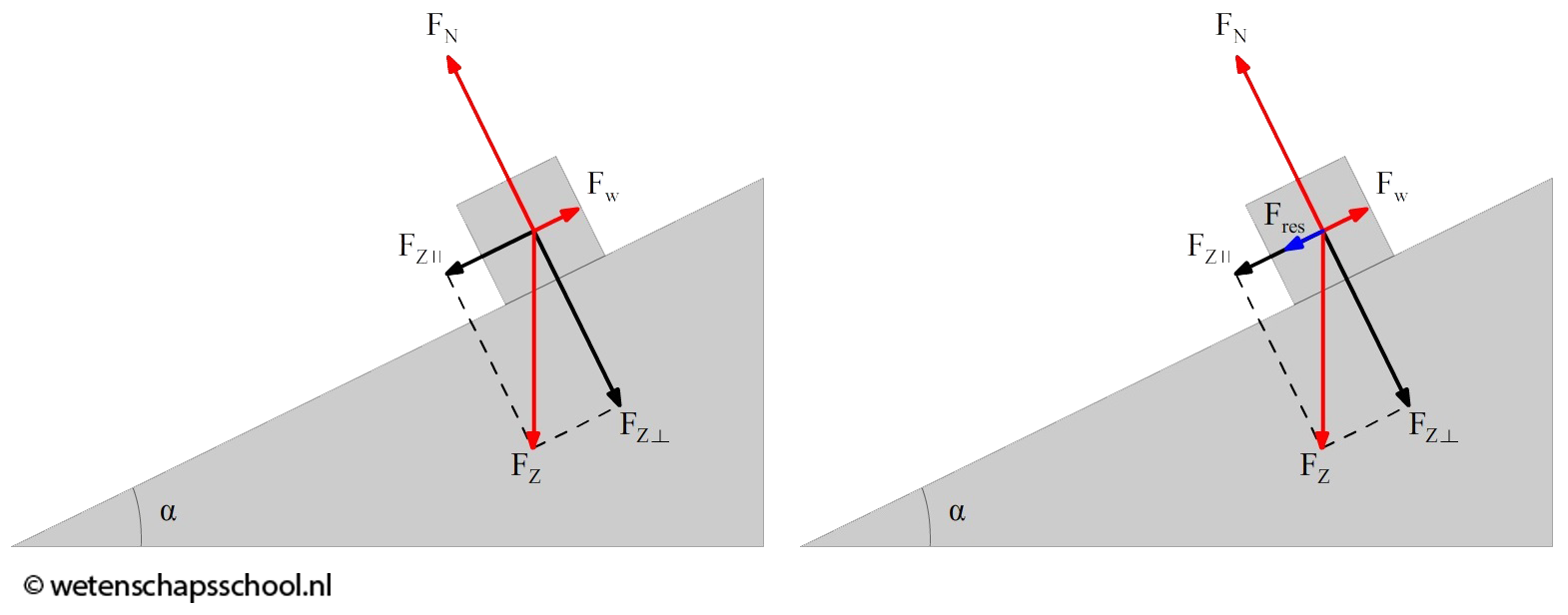
Klas 4
Hieronder zien we een blok op een hellend vlak. In de linker afbeelding is te zien dat Fz|| groter is dan Fw. Het resultaat is dat er een resulterende kracht op het blok werkt in de bewegingsrichting (zie de rechter afbeelding). Volgens de tweede wet zal dit blok dus versnellen.

In het onderstaande voorbeeld is Fw juist groter dan Fz||. Hier wijst de resulterende kracht dus tegen de bewegingsrichting in. Deze situatie doet zich voor als een blok afremt op de helling.








Training
    Rekenen met de formule Fres = ma
  1. (3,4) Leid de eenheid van de kracht af in SI-grondeenheden met behulp van de volgende formule: $$ F_{res} = ma $$
  2. (3,4) Hieronder is een (snelheid,tijd)-diagram weergegeven van een bewegend voorwerp met een massa van 3,0 × 103kg.
    1. Leg uit of de resulterende kracht gedurende de eerste 15 seconden constant is of niet.
    2. Bepaal met behulp van de grafiek op elk moment de resulterende kracht.
    3. Bepaal met behulp van de grafiek op elk moment of het voorwerp vooruit gaat of achteruit en in welke richting de kracht wijst.
  3. (3,4) Het onderstaande (v,t)-diagram beschrijft een sprong van een volleybalspeler met een massa van 75 kg.

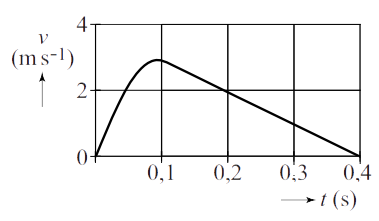
    1. Bepaal de resulterende kracht werkende op de springer op tijdstip t = 0 s.
    2. Bepaal de afzetkracht van de springer op tijdstip t = 0 s.
    (bron: examen VWO 2015-1)
  4. (3,4) Hieronder is het (v,t)-diagram van de beweging van een jojo weergegeven. Op tijdstip t = 0 s is het koord volledig om de jojo gewikkeld en laat de persoon de jojo los. De jojo heeft een massa van 85 gram.
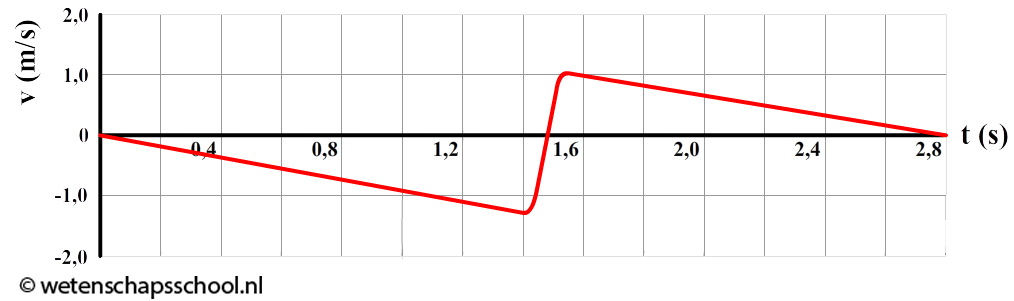    Bepaal de grootte van de kracht die de jojo in het laagste punt op de vinger van de persoon uitoefent.
  5. (3,4) Space Shot is een spectaculaire attractie in het pretpark Six Flags. Hierbij kan een groep mensen zich laten lanceren met behulp van een ring om een hoge toren. De massa van de ring met bezoekers is 2,4 × 103 kg. Hieronder zien we een (v,t)-diagram van de beweging.
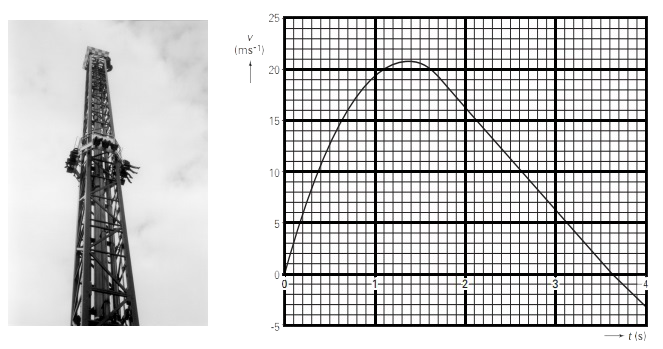
    1. Bepaal de motorkracht waarmee de ring wordt afgeschoten. Je mag de wrijvingskracht verwaarlozen.
    2. (4V) In werkelijkheid is de wrijvingskracht niet te verwaarlozen. Dit is bijvoorbeeld te zien aan de lichte knik in de grafiek op tijdstip t = 3,62 s (leg je geodriehoek op de grafiek om de knik goed te kunnen zien). Leg uit waarom we aan de aanwezigheid van deze knik kunnen zien dat er wel degelijk een wrijvingskracht werkt.
    (bron: examen VWO 2003-1)
  6. (3,4) Een auto met een massa van 1,6 × 103 kg versnelt eenparig gedurende 4,0 seconden. De beginsnelheid van de auto is 80 km/h. De auto ervaart een constante wrijvingskracht van 1,2 × 104 N en de motorkracht is gelijk aan 1,8 × 104 N. Bereken de snelheid van de auto na de versnelling.
  7. (3,4) Een auto met een massa van 3,0 x 103 kg versnelt eenparig van 50 km/h naar 70 km/h in een tijdsduur van 12 seconden. De motorkracht van de auto tijdens de beweging heeft een constante waarde van 1,5 x 103 N.
    1. Bereken de grootte van de wrijvingskracht tijdens deze versnelling.
    2. (4V) De totale wrijvingskracht bestaat uit rolwrijving en luchtwrijving. Een van de twee wrijvingskrachten is bij deze beweging verwaarloosd. Leg uit welke.
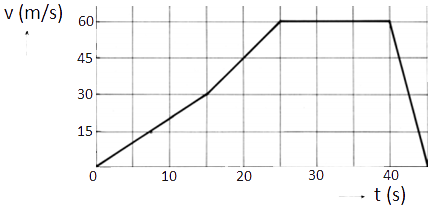
  8. (4V) Op een lange rechte weg rijdt een auto met constante snelheid. Op t = 20 s besluit de chauffeur te versnellen. Hij trapt hiervoor zijn gaspedaal verder in (zie het onderstaande diagram). De massa van auto met chauffeur is 1,0 × 103 kg.

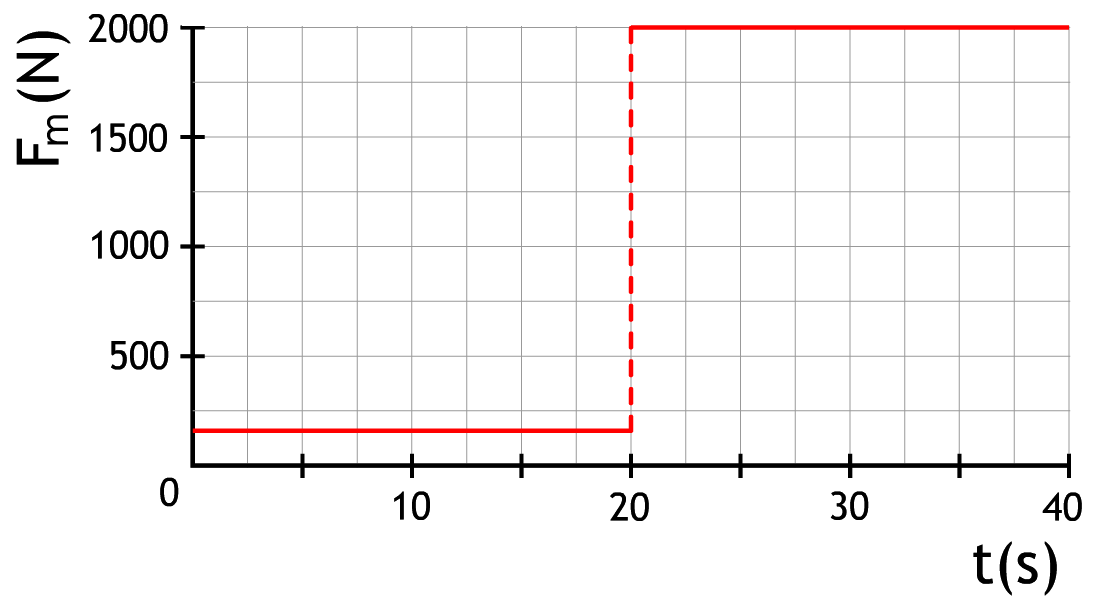
    1. Bepaal de grootte van de wrijvingskracht op de auto vóór het versnellen. Verklaar je antwoord.
    2. Bepaal de versnelling direct na het tijdstip t = 20 s. Leg eerst uit hoe groot de wrijvingskracht op dit moment is.
    3. De snelheid van de auto is als functie van de tijd weergegeven in het onderstaande diagram.

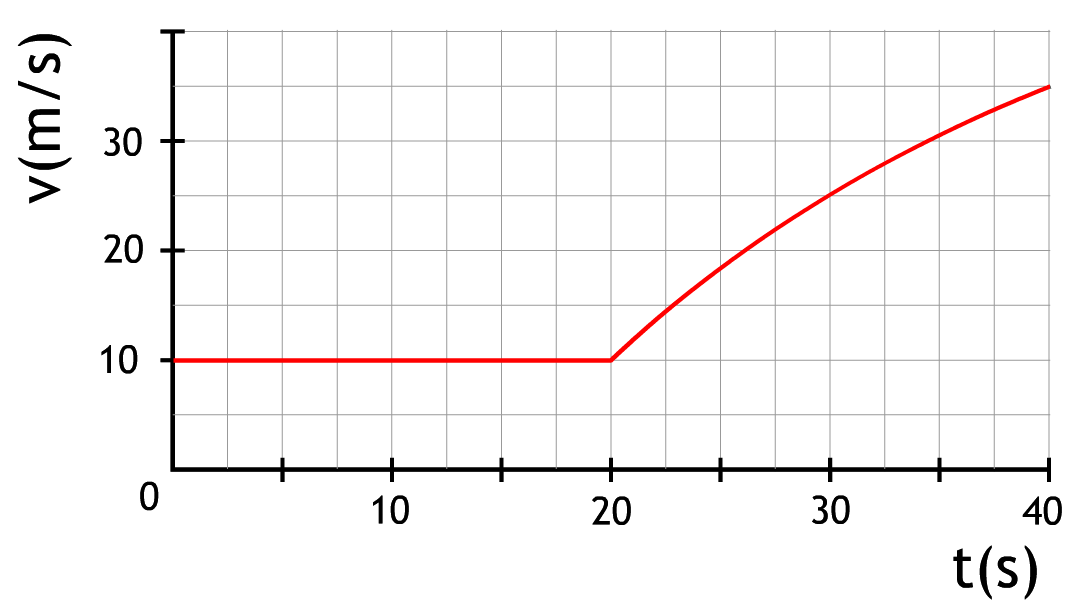
      Bepaal de grootte van de wrijvingskracht op tijdstip t = 30 s.
  9. (3,4) In een bergachtig gebied kunnen toeristen met een bergtrein naar een mooi uitzichtpunt reizen. De trein begint met aan een rit naar boven. In het onderstaande (v,t)-diagram zijn de eerste 40 seconden van deze rit beschreven. De hoek tussen de rails en de horizon is gedurende de hele rit 28 graden en de massa van de trein is 13 × 103 kg.
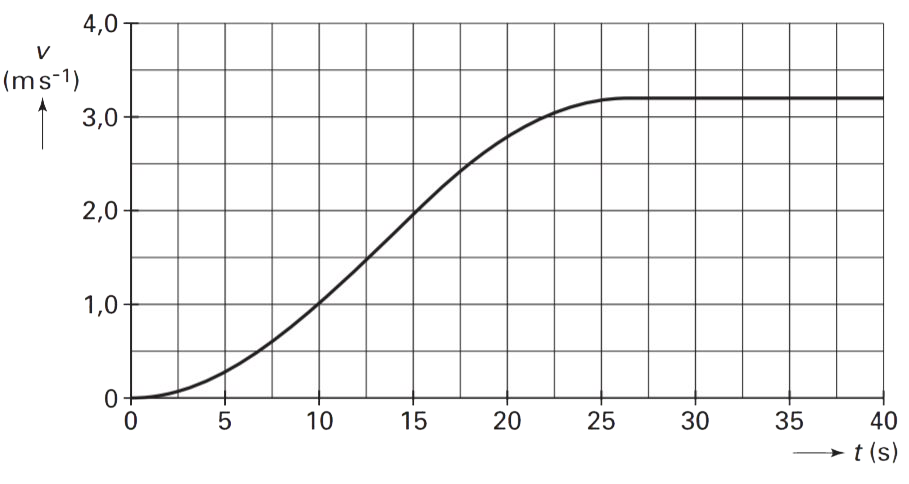
    1. Op tijdstip t = 15 s oefent de trein een motorkracht uit van 66 kN. Bereken de rolwrijvingskracht en de rolwrijvingscoëfficiënt. Je mag aannemen dat de luchtwrijvingskracht verwaarloosbaar is.
    2. Leg uit of de rolwrijvingskracht op een steilere helling groter of kleiner is.
    (bron: examen VWO 2004-1)
  10. (3,4) Een fietser trekt vanuit stilstand op met een constante spierkracht van 110 N. De massa van de racefiets en de fietser tezamen is 100 kg. De rolwrijvingskracht is 20 N. De luchtwrijvingskracht laten we nog even buiten beschouwing.
    1. Bereken de versnelling van de fietser.
    2. In werkelijkheid speelt de luchtwrijving natuurlijk een grote rol tijdens het fietsen. Het zorgt er zelfs voor dat de snelheid van de fietser op den duur niet meer toeneemt. De luchtwrijvingskracht wordt gegeven door: $$ F_{w,lucht} = kv^2 $$ De constante k heeft voor dit voorwerp een waarde van 0,52 kg/m.
      Bepaalde de uiteindelijke snelheid van de fietser.
  11. (3,4) Hieronder zien we een (F,t)- en een (v,t)-diagram van een zwemmer die een volledige zwemslag maakt.
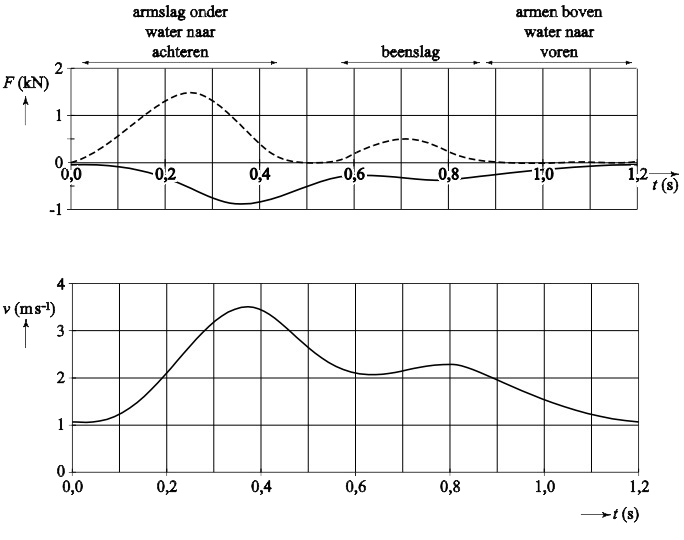
    1. Het tijdstip waarop de snelheid maximaal is, valt later dan het tijdstip waarop de voortstuwingskracht maximaal is. Verklaar dit.
    2. Op tijdstip t = 0,37 s is de snelheid even constant. Verklaar dit.
    3. Na tijdstip t = 0,37 s is de wrijvingskracht voor een tijdje groter dan de spierkracht. Wat zegt dit over de beweging van de persoon? Leg uit of de zwemmer hier even vooruit of achteruit beweegt. Geef ook aan of de zwemmer versnelt of vertraagt.
    (bron: examen VWO 2011-2)
  12. (3,4) Een leerling wil een bungeejump maken. Op een hoog platform wordt een 15 meter lang elastisch koord aan hem vastgemaakt. De leerling laat zich dan zonder beginsnelheid van het platform vallen. In het laagste punt van de sprong is het koord 20 m uitgerekt.
    In de schematische tekening zijn een aantal punten met letters aangegeven. P is het platform waar de sprong begint. R is de plaats (15 m onder P) waar het koord begint uit te rekken. E is de evenwichtsstand waar de leerling aan het einde van de sprong in rust blijft hangen. D is het laagste punt (35 m onder P). Beredeneer of de leerling op het traject van R naar E versnelt of vertraagt. Verwaarloos hierbij de wrijvingskrachten.
    (bron: examen VWO 2001-1)
  13. (4) Een auto met een massa van 2200 kg wordt weggetakeld met behulp van een kabel. De kabel zit onder een hoek van 23 graden met de horizontaal aan de auto vast. De spankracht in de kabel is 450 N. In eerste instantie laten we de wrijvingskrachten buiten beschouwing.
    1. Bereken de snelheid van de auto na 5,0 s als er geen wrijvingskracht werkt.
    2. (4V) In werkelijkheid werkt er natuurlijk wel een wrijvingskracht. De wrijvingscoëfficiënt van het contactoppervlak tussen de banden van de auto en de weg is 0,007. Bereken nogmaals de snelheid van de auto na 5,0 s.
  14. (4) Een vliegtuig stijgt onder een hoek van 15 graden omhoog de lucht in. De massa van het vliegtuig is 20 × 103 kg en het vliegtuig versnelt met 0,95 m/s2. De voorwaartse kracht op het vliegtuig (de stuwkracht) is 11 × 104 N. Loodrecht op de vleugels van het vliegtuig werkt de zogenaamde liftkracht.
    1. Bereken de grootte van de liftkracht.
    2. Bereken de grootte van de luchtwrijvingskracht.
  15. (4V) Een blokje van 125 gram ligt op een plank. Wanneer je de plank kantelt, begint vanaf α = 25° het blokje met een constante snelheid naar beneden te glijden. Bereken de versnelling van het blokje als de helling gelijk is aan α = 35°. (Tip: Vind in de eerste situatie eerst de wrijvingscoëfficient f).
  16. (4V) Een leerling glijdt op haar slee met een versnelling van 3,0 m/s2 een helling af. De massa van de leerling en haar slee zijn samen 41 kg. De leerling ondervindt een wrijvingskracht van 90 N. Bereken de hellingshoek α. Ondersteun jouw berekening met een schets.
  17. (4V) Een blok versnelt vanuit stilstand van een plank met een versnelling van 0,2 m/s2. De helling van de hoek is gelijk aan 30°. De wrijvingskracht is gelijk aan 30 N.
    1. Bereken de massa van het blokje.
    2. Na 3,0 seconden is de snelheid van het blokje 0,6 m/s geworden. Leg uit of de schuifwrijvingskracht nu groter of kleiner is geworden of gelijk is gebleven.

    18. Toetsvragen

  18. Hieronder zien we een rail met in het midden een knik. Op de rail wordt een karretje gezet, zoals hieronder te zien is. De afbeelding is niet op schaal.

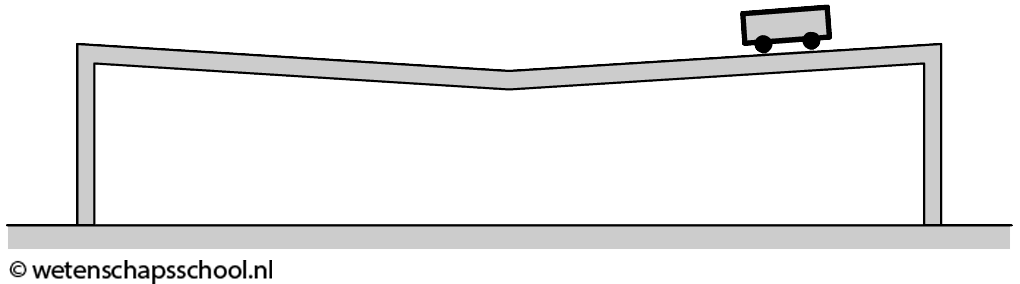    De kar wordt vanuit de afgebeelde positie op het tijdstip t = 0 s losgelaten. Dit tijdstip noemen we tA. De kar gaat dan over de rail heen en weer bewegen. Het laagste punt van de baan noemen we de evenwichtsstand. De snelheid langs de baan van het zwaartepunt van de kar is hieronder als functie van de tijd weergegeven. Als de kar naar links beweegt, is de snelheid negatief gekozen.
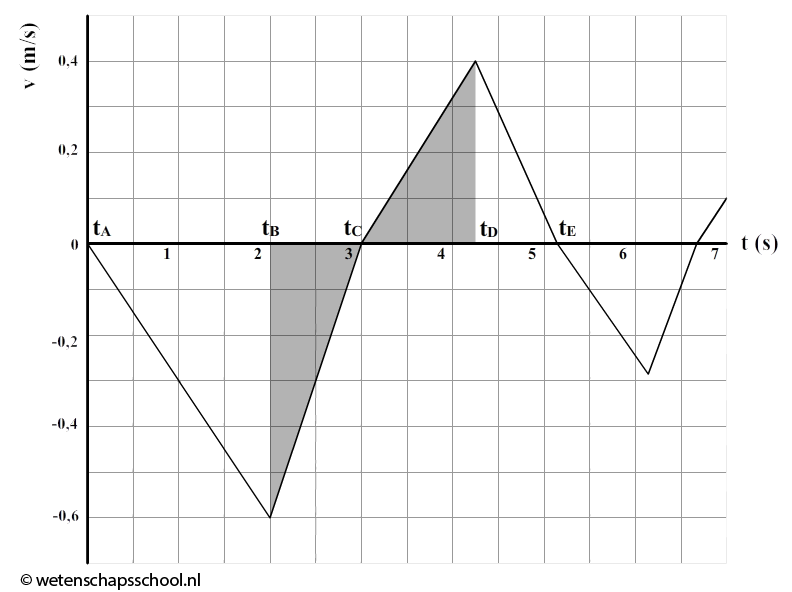
    1. Leg uit waar het karretje zich bevindt op tijdstip tc
    2. Hoe kan je aan het diagram zien dat er wrijvingskracht werkt?
    3. Bepaal de versnelling van de kar tussen tb en tc en tussen c en td.
    4. (4) De kar ondervindt tijdens zijn beweging een constante wrijvingskracht. Leg uit waarom de versnelling tussen tb en tc en tussen c en td dan toch anders is.
    5. (4V) Bepaal de wrijvingskracht op de kar. Neem hiervoor aan dat de massa van het karretje gelijk is aan 43 gram (heftige vraag!).
    (bron: examen VWO 1986-2)