In deze paragraaf gaan we bepalen hoe groot de totale kracht is die op een voorwerp werkt als er meerdere krachten op werken. We noemen deze totale kracht de resulterende kracht.

De totale kracht die op een voorwerp werkt noemen we de resulterende kracht (F_res). Hieronder zien we twee personen die beide een kracht uit oefenen op een kar. De linker persoon oefent een kracht van 100 N uit en de rechter persoon een kracht van 125 N. In totaal oefenen ze dus een kracht naar rechts uit van 100 + 125 = 225 N. Er geldt dus:

$$ F_{res} = 225 \text{ N} $$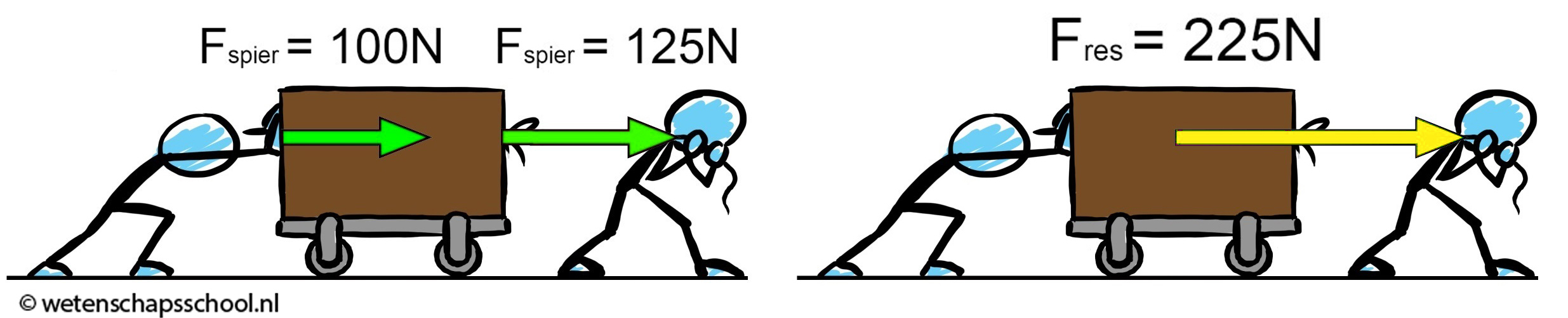

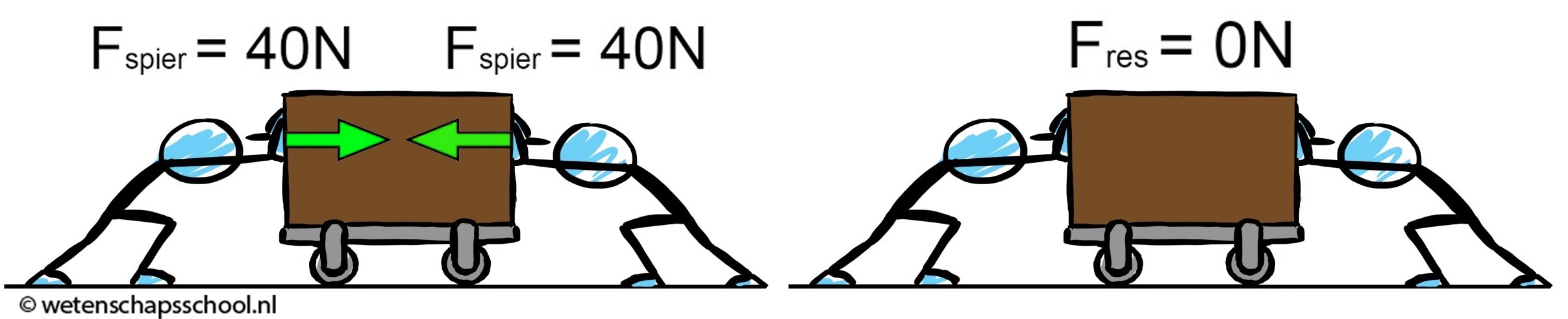
Hieronder werken twee krachten juist tegen elkaar in. We vinden nu een resulterende kracht van 40 - 40 = 0 N.

In de onderstaande afbeelding oefent één persoon een kracht van 100 N uit en de andere persoon een kracht van 40 N. De linker leerling oefent dus een 60 N grotere kracht uit dan de rechter leerling. De resulterende kracht is dus 60 N en wijst naar links.

Klas 4

De algemene formule voor de resulterende kracht is: $$ \vec{F}_{res} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + ... $$ We kunnen dit afkorten tot:

$$ \vec{F}_{res} = \sum{\vec{F}} $$

Resulterende kracht (F_res)	newton (N)
Som van alle krachten (ΣF)	newton (N)

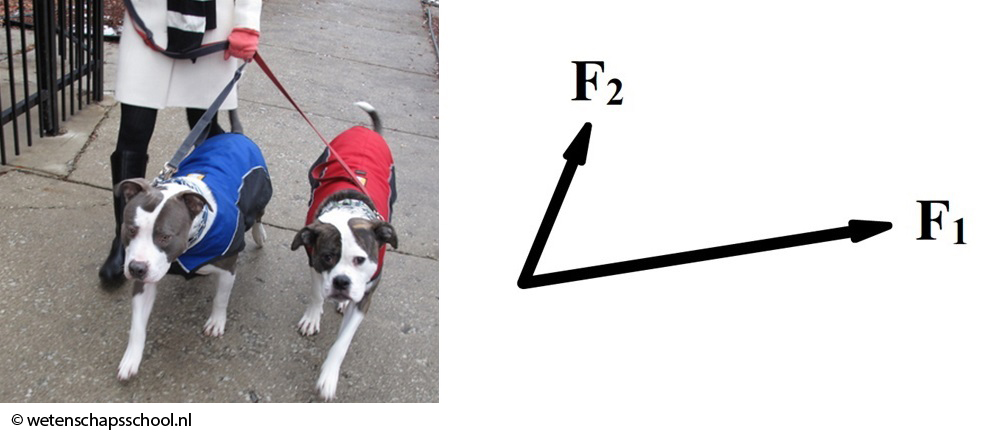
Het sommatieteken $\Sigma$ staat voor 'de som van'. Er staat hier dus dat de resulterende kracht gelijk is aan de som van de individuele krachten. De pijltjes boven de krachten geven aan dat we bij deze optelling wel rekening moeten houden met de richting van de krachten. Als twee krachten bijvoorbeeld tegen elkaar in werken, dan moeten we de krachten niet bij elkaar optellen, maar juist van elkaar aftrekken.

Maar wat nu als de krachten onder een willekeurige hoek werken? De twee honden in de volgende afbeelding kunnen bijvoorbeeld elk een spankracht uitoefenen op de hand van hun baasje in een willekeurige richting.

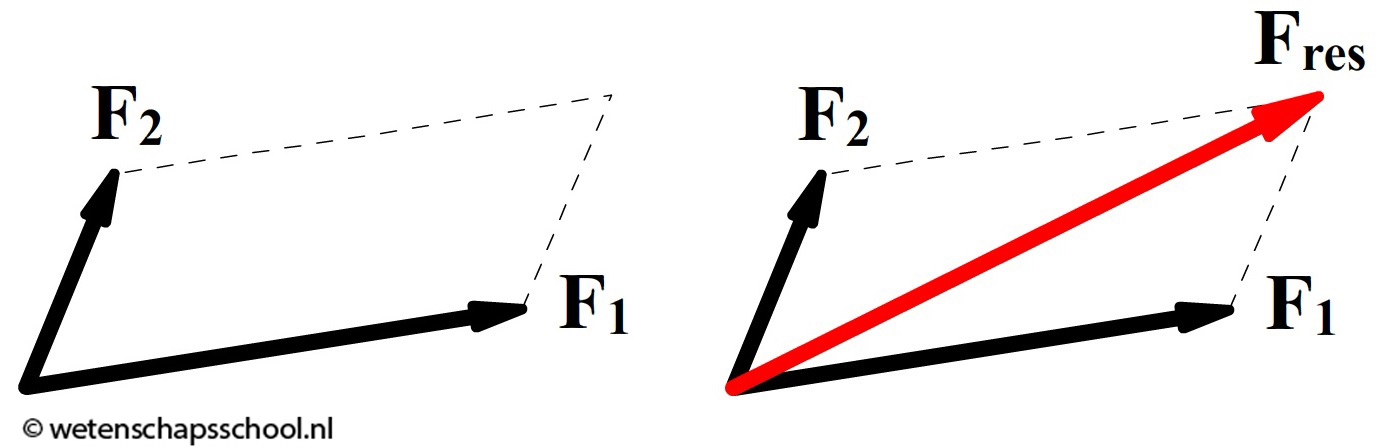
In dit geval gebruiken we voor het 'optellen van de krachten' de parallellogrammethode. Een parallellogram is een vierhoek, waarbij de tegenoverstaande zijden parallel aan elkaar lopen en even lang zijn. In de onderstaande afbeelding is te zien hoe met het parallellogram de resulterende kracht te bepalen is.

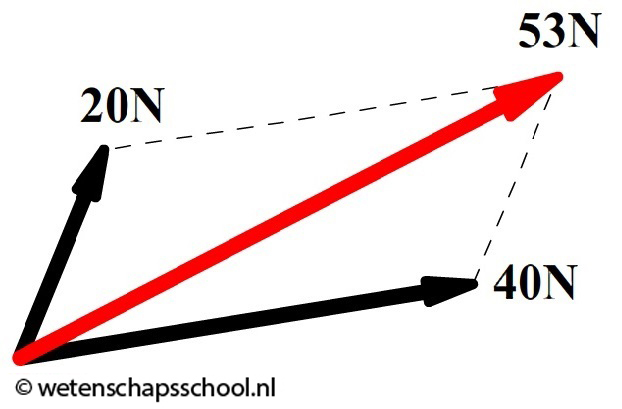
In de onderstaande afbeelding zien we dat kracht F₁ gelijk is aan 40 N en kracht F₂ aan 20 N. Als we de schaal bepalen en hiermee de grootte van de resulterende kracht opmeten en uitrekenen, dan vinden we 53 N. Merk op dat 20 + 40 ≠ 53. Het 'optellen van krachten' met een parallellogram werkt dus niet zoals je normaal gesproken optelt!

In het onderstaande voorbeeld is het parallellogram een simpel rechthoek bestaande uit twee rechthoekige driehoeken. In dit geval kunnen we daarom gebruik maken van de stelling van Pythagoras om de resulterende kracht te berekenen:

$$ a^2 + b^2 = c^2 $$ $$ c = \sqrt{a^2 + b^2} $$ $$ c = \sqrt{20^2 + 40^2} = 45 \text{ N} $$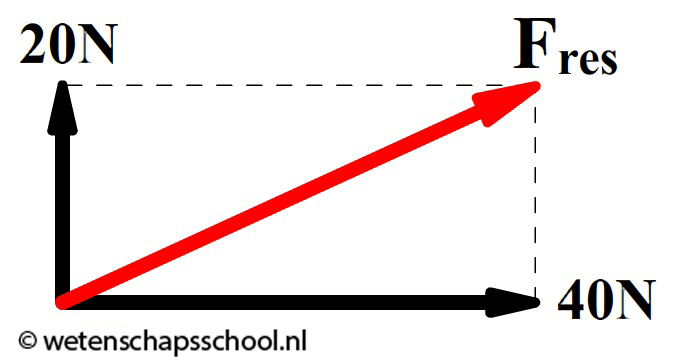

Training

Rekenen met de resulterende kracht met krachten die in dezelfde of in tegenovergestelde richting werken

(2,3) Twee leerlingen zijn aan het touwtrekken. De linker persoon oefent een kracht van 20 N uit en de rechter persoon een kracht van 15 N. Teken de resulterende kracht op schaal. Je kan bijvoorbeeld kiezen voor een schaal waarbij elke centimeter van de vectorpijl staat voor 5 newton.
(2,3) Een persoon oefent een kracht van 45 N op een kar uit. De wrijvingskracht is gelijk aan 20 N. Bereken de grootte van de kracht en geef ook de richting van de kracht aan.
(2,3,4) De wrijvingskracht op een kar is 40 N. De resulterende kracht is 20 N naar rechts. Bereken de spierkracht van de persoon.
(2,3,4) Twee leerlingen zijn aan het touwtrekken. De linker persoon oefent een kracht van 65 N uit. De resulterende kracht is gelijk aan 35 N en wijst naar rechts. Teken de spierkracht van de rechter persoon op schaal.

Rekenen met de parallellogrammethode

(2,3,4) Teken zes verschillende parallellogrammen. Varieer in grootte en oriëntatie. Maak ze zo verschillend mogelijk. Check telkens of de tegenoverstaande zijden parallel aan elkaar lopen. Op deze manier leer je een goed gevoel te krijgen voor hoe een parallellogram eruit ziet. Zorg dat je in één oogopslag kan zien of een figuur een parallellogram is of niet.
(2,3,4) In de onderstaande afbeelding werken er telkens twee krachten op een voorwerp. Teken telkens de resulterende kracht. Meet van het midden van het bolletje tot de punt van de pijl.
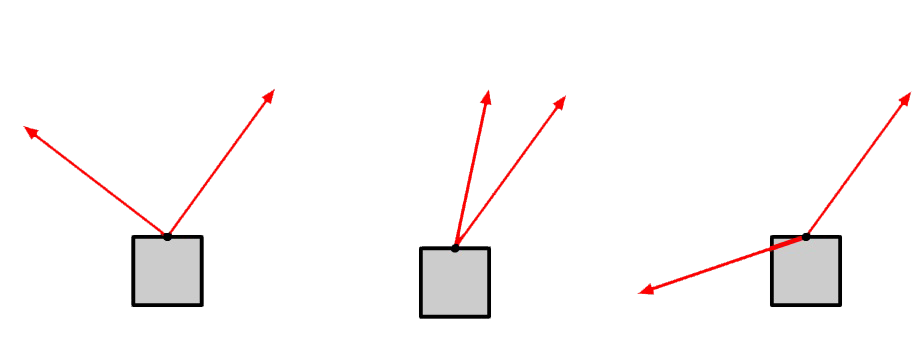
(2,3,4) Bepaal in de volgende afbeelding de grootte van de linker kracht en van de resulterende kracht. Zorg dat je op de millimeter nauwkeurig meet.
(2,3) Teken zelf nog minimaal drie keer een krachtenpaar en teken de resulterende kracht. Varieer maximaal in grootte en richting van de krachten. Ga door tot je snel en flexibel op het antwoord komt.
(2,3) Teken in de volgende twee afbeeldingen de resulterende kracht op schaal. Bepaal daarna de grootte van deze kracht.
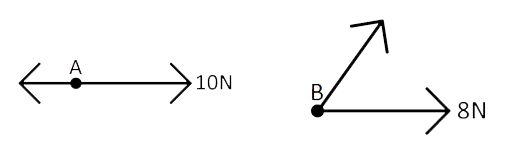
(2,3,4) In de volgende afbeeldingen trekken twee kleine sleepbootjes een grotere boot voort. Teken de resulterende kracht. Bepaal daarna de grootte van deze kracht.
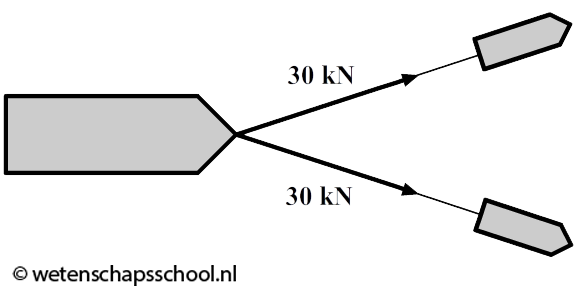
1. (2,3,4) Teken in de volgende afbeelding de resulterende kracht op schaal. Bepaal daarna de grootte van deze kracht.
2. (3,4) Ga nu met de stelling van Pythagoras na dat jouw antwoord bij vraag a klopt.
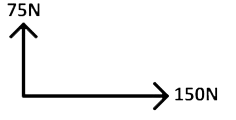
(3,4) Een kracht van 50 N staat loodrecht op een kracht van 20 N. Bereken de resulterende kracht. (Let op! Het woord 'bereken' wil zeggen dat je de pijlen niet mag opmeten om op het antwoord te komen. Als er staat 'bepaal', dan mag dit wel)
(3,4) Leg uit wat het verschil is tussen 'berekenen' en 'bepalen'.