Als atomen in een voorwerp trillen, dan zenden ze een heel spectrum aan straling uit. We noemen dit het planckspectrum. In deze paragraaf gaan we dit spectrum bestuderen.

In het hoofdstuk 'warmte' hebben we geleerd dat atomen in een materiaal met een temperatuur boven de 0 kelvin zijn continu aan het trillen. In dat hoofdstuk hebben we echter niet besproken dat trillende atomen straling uitzenden. Omdat zo goed als elk materiaal een temperatuur heeft boven de 0 K, kunnen we dus stellen dat zo goed als elk materiaal in het universum straling uitzendt. Meestal zit deze straling echter buiten het zichtbare spectrum. De aarde en ook wijzelf geven bijvoorbeeld voornamelijk infraroodstraling af.

Als de temperatuur van een voorwerp hoog genoeg wordt, dan komt er een moment dat de straling wel zichtbaar wordt. Dit zien we bijvoorbeeld in de onderstaande afbeelding. Een stuk metaal is hier sterk verwarmd en begint hierdoor te gloeien in het rode deel van het spectrum.

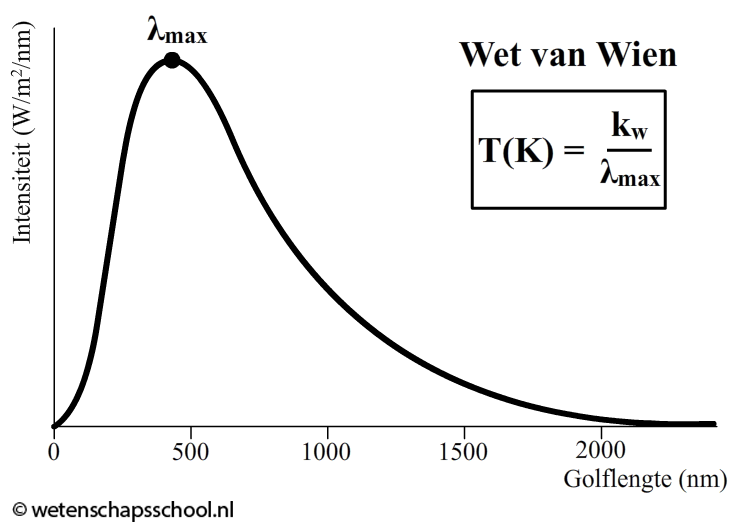
Het licht dat op deze manier ontstaat heeft een karakteristiek stralingsspectrum, genaamd de planckkromme of het planckspectrum. In de onderstaande animatie is te zien hoe dit spectrum eruit ziet bij verschillende temperaturen. We geven dit spectrum hieronder weer met op de horizontale as de golflengte van de straling en op de verticale as de intensiteit van deze straling.

Bij een lage temperatuur zit de straling bijna volledig in het infrarode deel van het spectrum. Als gevolg kunnen we deze straling niet waarnemen met onze ogen. Als de temperatuur hoger wordt, dan komt er een moment dat er genoeg rood licht wordt geproduceerd, zodat we dit met onze ogen kunnen zien. Als we de temperatuur nog meer verhogen, dan komt er een moment dat er in het hele zichtbare spectrum veel licht wordt uitgezonden. Als we alle kleuren licht tegelijk in onze ogen krijgen, dan zien we dit als wit licht. Als de temperatuur nog hoger wordt, dan gaat op een gegeven moment het blauwe licht domineren.

Hoe hoger de temperatuur van een object, hoe meer de piek van de planckkromme zich naar links verplaatst (naar een kleinere golflengte). Een blauwe ster heeft dus een hogere temperatuur dan een witte ster en een witter ster heeft een hogere temperatuur dan een rode ster. De relatie tussen de golflengte van de piek en de temperatuur noemen we de wet van Wien:

$$ \lambda_{max} = \frac{k_w}{T} $$

De golflengte van de piek (λ_max)	meter (m)
De constante van Wien (k_w)	2,8977721 × 10^-3 Km
Oppervlaktetemperatuur (T)	kelvin (K)

De temperatuur moet in deze formule worden gegeven in kelvin. Er geldt:

$$ T(K) = T(^\circ C) + 273 $$

Met deze formule kunnen we bijvoorbeeld de oppervlaktetemperatuur van de zon berekenen. De piek van het stralingsspectrum van onze zon ligt bij de 500 nm. De oppervlaktetemperatuur is dus:

$$ T = \frac{k_w}{\lambda_{max}} $$ $$ T = \frac{2,8977721 \times 10^{-3}}{500 \times 10^{-9}} = 5,80 \times 10^3 \text{ K} $$

4VWO

Met het oppervlak onder een planckkromme kunnen we de totale intensiteit van een lichtbron berekenen. In de onderstaande afbeelding is bijvoorbeeld alleen het zichtbare deel van een planckkromme afgebeeld. Als we de totale intensiteit van dit zichtbare gedeelte willen weten, dan willen de intensiteit van alle golflengtes in dit gebied bij elkaar optellen en dat is gelijk aan het oppervlak onder de grafiek.

4VWO

De SI-eenheid van de intensiteit (I) is de hoeveelheid joule die per seconde op een oppervlak van een vierkante meter valt en dit is gelijk aan W/m². De intensiteit is te relateren aan het totale vermogen (P) dat een lichtbron uitzendt. We noemen het vermogen als het gaat om een lichtbron ook wel de lichtsterkte (L). Er geldt:

$$ I = \frac{P_{bron}}{4\pi r^2} $$ $$ I = \frac{L}{4\pi r^2} $$

Intensiteit (I)	watt per vierkante meter (W/m²)
Vermogen van de bron (P_bron)	watt (W)
Straal vanaf het centrum van de bron (r)	meter (m)
Lichtsterkte (L)	watt (W)

We zien aan de formule dat de intensiteit kwadratisch afneemt met de afstand van de bron. We noemen deze formule daarom ook wel de kwadratenwet. In de onderstaande afbeelding is goed te zien waarom de intensiteit op deze manier afneemt. Hoe verder de straling komt, over hoe groter oppervlak de straling verdeeld wordt.

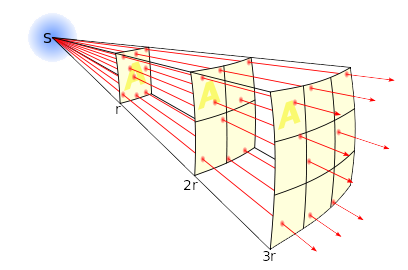
De intensiteit van de zon op aarde noemen we de zonneconstante. De waarde hiervan is te vinden in BINAS 32C. Ook de lichtsterkte van de zon is in deze tabel te vinden. We gebruiken voor de lichtsterkte van de zon het symbool $L_\odot $.

We kunnen het vermogen (P) van een lichtbron ook relateren aan de oppervlaktetemperatuur (T). Deze relatie wordt de wet van Stefan-Boltzmann genoemd:

$$ P_{bron} = \sigma A T^4 $$ $$ L = \sigma A T^4 $$

Vermogen van de bron (P)	watt (W)
De constante van Stefan-Boltzmann (σ)	5,670373 × 10^-8 W/m²/K⁴
Oppervlak van de bron (A)	vierkante meter (m²)
Oppervlaktetemperatuur (T)	kelvin (K)
Lichtsterkte (L)	watt (W)

Ter afsluiting nog een paar veelgebruikte afstandsmaten in de sterrenkunde. Afstanden in het zonnestelsel meten we vaak in astronomische eenheden (AE). 1 AE is gelijk aan de afstand van de aarde tot de zon, oftewel 1,49598 × 10¹¹ m. Afstanden tot sterren worden vaak gemeten in lichtjaar. Dit is de afstand die licht in een jaar aflegt, oftewel 9,461 × 10¹⁵ m.

Training

Rekenen met de wet van Wien

Welke gegevens van een ster kan je achterhalen met een absorptiespectrum?
Hieronder zien we het spectrum van onze zon. Bepaal hieruit de oppervlaktetemperatuur van de zon in graden Celsius.
Het menselijk lichaam zendt infraroodstraling uit. Laat met behulp van een schatting en een berekening zien dat dit het geval is.
Bij een brandende gloeilamp heeft de gloeidraad een temperatuur van 2,5 × 10³ K. Leg met een berekening uit waarom het rendement van een gloeilamp zo laag is.
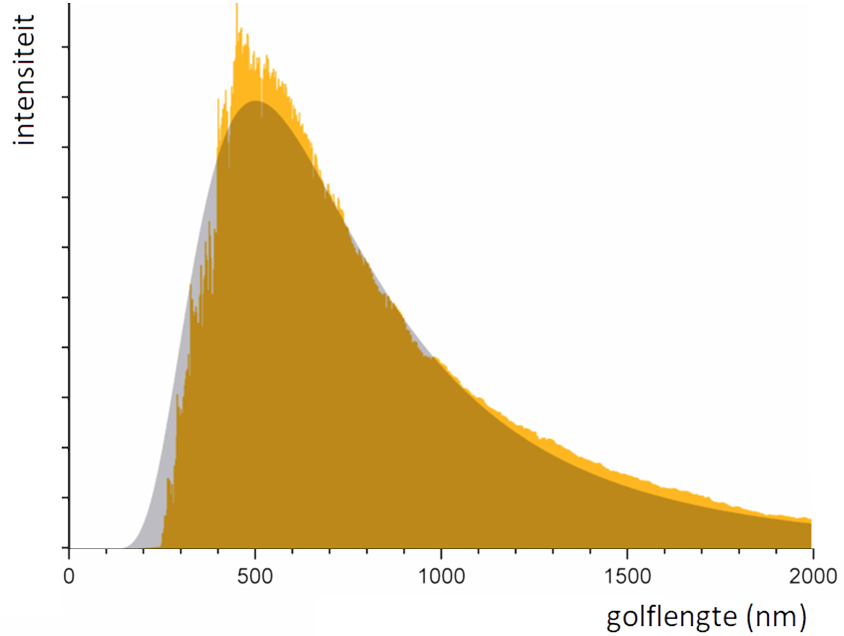
De temperatuur van een gloeidraad is te bepalen door het uitgezonden stralingsspectrum te vergelijken met de planck-kromme van dezelfde temperatuur. In de onderstaande figuren is de onderste kromme steeds van de gloeidraad en de bovenste kromme een planck-kromme.
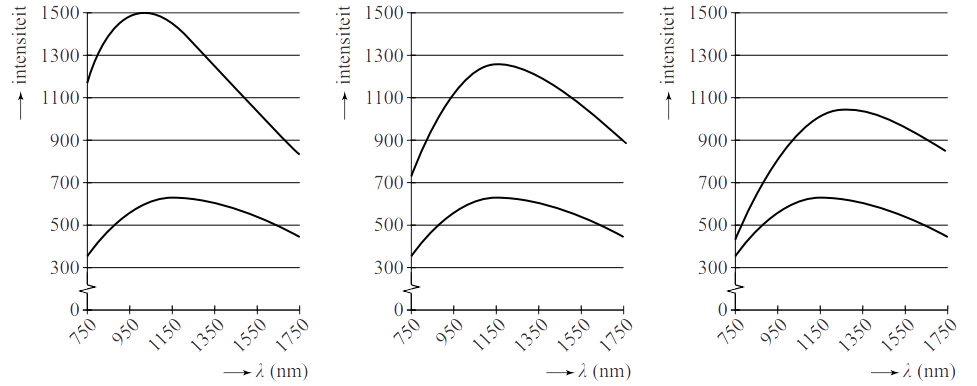
1. Leg uit in welke figuur de planck-kromme met dezelfde temperatuur als de gloeidraad staat.
2. Bepaal de temperatuur van de gloeidraad in graden Celsius.
(bron: examen VWO 2017-2)
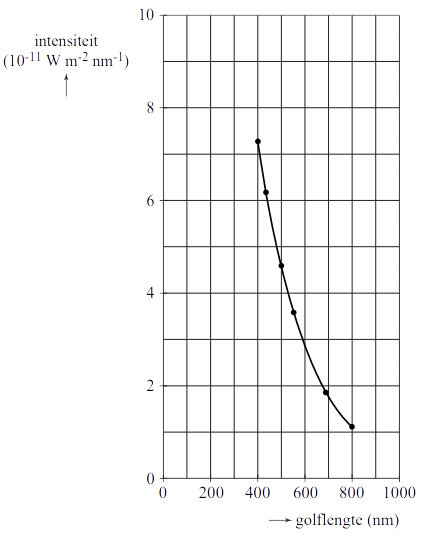
Van de ster Wega is de stralingsintensiteit in het zichtbare gebied als functie van de golflengte bepaald (zie de onderstaande afbeelding).
1. Toon met behulp van het diagram aan dat de temperatuur van Wega hoger is dan 7000 K.
2. (V) De stralingsintensiteit die we van Wega meten is 2,9 × 10^-8 Wm^-2. Een percentage hiervan ligt in het zichtbare gebied. Bepaal dit percentage.
(bron: examen VWO 2011-pilot)
De WMAP doet metingen aan de zogenaamde kosmische achtergrondstraling. Dit is straling die overal in het universum te meten is. Hieronder zijn de metingen in een diagram weergegeven:
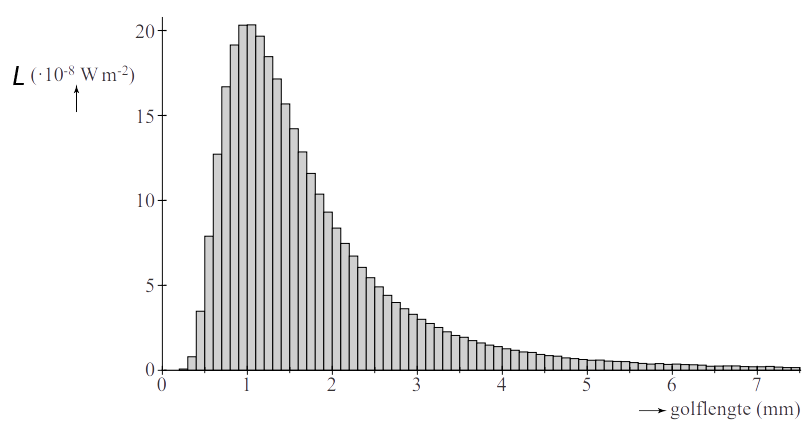
1. 4VWO Bereken de orde van grootte van de hoeveelheid fotonen met een golflengte tussen 1,0 en 2,0 mm, die per seconde op een vierkante meter terechtkomen.
2. Bereken de temperatuur behorend bij de achtergrondstraling.
(bron: examen VWO 2015-pilot)

Rekenen met de wet van Stefan-Boltzmann en de kwadratenwet

(V) In een gloeilamp met een vermogen van 25 W zit een gloeidraad met een lengte van 25 mm en een diameter van 0,20 mm. Bereken de temperatuur van de gloeidraad.
(V) Een gloeilamp brandt eerst met een temperatuur van 2000 K en dan met 4000 K. Beredeneer met welke factor het vermogen is toegenomen.
(V) Op aarde ontvangen we maximaal 1,368 × 10³ W/m² aan licht van de zon. Dit wordt de zonneconstante genoemd. Gebruik de afstand tot de zon en reken hiermee uit hoeveel energie de zon per seconde omzet.
(V) De zon zend per seconde 2,0 × 10³⁸ neutrino's uit. Bereken hoeveel neutrino's er per seconde op de aarde terecht komen.
(V) De ster Wega heeft gemeten vanaf de aarde een intensiteit van 2,9 x 10² W/m². Het uitgestraald vermogen van Wega is groter dan dat van de zon. Bereken hoeveel maal zo groot.
(V) Een ster met dezelfde kleur als de zon heeft een 81x zo grote lichtsterkte. Beredeneer hoeveel groter de diameter dan deze ster is ten opzichte van de zon.
(V) De ster Betelgeuze heeft ongeveer dezelfde temperatuur als de ster Proxima Centauri. Toch is Betelgeuze vanaf de aarde gezien 109x feller. Bereken hoeveel keer de straal van Betelgeuse groter is ten opzichte van Proxima Centauri.