Dit hoofdstuk gaat over de eigenschappen van straling (licht). We beginnen deze paragraaf met het stralingsspectrum.
Als we licht van een gloeilamp door een prisma schijnen, dan krijgen we een volledige 'regenboog' aan kleuren te zien. We noemen dit een continu spectrum (zie de onderstaande afbeelding).
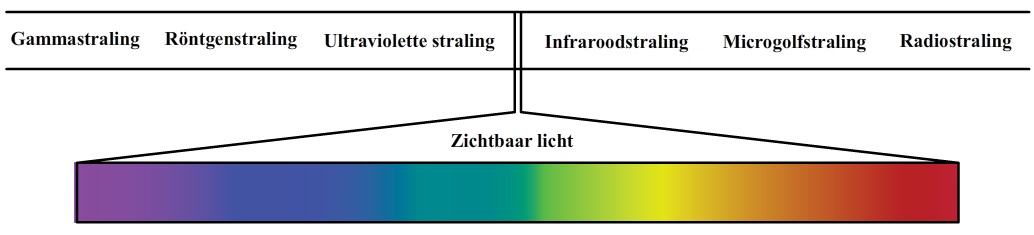
Naast het zichtbare deel van het spectrum, is er ook straling die we met onze ogen niet kunnen zien. Links van het paarse deel van het spectrum bevindt zich bijvoorbeeld ultravioletstraling, röntgenstraling en gammastraling. Rechts van het rode deel van het spectrum hebben we infrarode straling, microgolfstraling en radiostraling. Zoals je in de onderstaande afbeelding kan zien is het zichtbare deel van het spectrum maar een klein deel van het gehele spectrum.
Licht bestaat uit kleine deeltjes die we fotonen noemen. Het verschil tussen verschillende kleuren licht zit hem in de frequentie (f) van de fotonen. Elk foton met een bepaalde frequentie heeft ook zijn eigen fotonenergie (Ef). Deze energie kan als volgt berekend worden:
| Energie (Ef) | joule (J) |
| Constante van Planck (h) | 6,62606957 × 10-34 Js |
| Frequentie van foton (f) | hertz (Hz) |
In het hoofdstuk trillingen hebben we gezien dat f = v/λ. Deze formule kunnen we ook toepassen op het foton. Als we voor de snelheid de lichtsnelheid (c) invullen, dan vinden we:
| Energie (Ef) | joule (J) |
| Constante van Planck (h) | 6,62606957 × 10-34 Js |
| Lichtsnelheid (c) | 3,0 × 108 m/s |
| Golflengte van foton (λ) | meter (m) |
Vraag: Door een LED-lamp loopt een stroomsterkte van 50 mA. Sommige elektronen die door de LED stromen zorgen voor het uitzenden van een blauw foton met een golflengte van 470 nm. Het totale vermogen van het uitgezonden licht is 0,075 W. Bereken hoeveel procent van de elektronen een blauw foton heeft uitgezonden.
Antwoord: Ten eerste kunnen we het aantal elektronen uitrekenen dat door de draad stroomt. In BINAS vinden we dat de lading van een elektron gelijk is aan e = 1,602×10-19 C. Daarnaast betekent een stroomsterkte van 0,050 A dat er 0,050 coulomb per seconde door de LED stroomt. Het totaal aantal elektronen dat per seconde door de LED stroomt, is dus gelijk aan:
$$ \frac{0,050}{1,602 \times 10^{-19}} = 3,12 \times10^{17} \text{ elektronen per seconde} $$We kunnen ook uitrekenen hoeveel fotonen er per seconde vrijkomen. Hiervoor berekenen we eerst de energie van één blauw foton:
$$ E_f = h\frac{c}{\lambda} $$ $$ E_f = 6,63\times 10^{-34}\times \frac{ 3,00\times 10^8}{470\times 10^{-9}}=4,23\times 10^{-19} \text{ J} $$Een vermogen van 0,075 W vertelt ons dat er 0,075 joule per seconde aan licht vrijkomt. Hiermee kunnen we het aantal fotonen per seconde uitrekenen:
$$ \frac{0,075}{4,23\times 10^{-19}} = 1,8 \times 10^{17} \text{ fotonen per seconde} $$Nu kunnen we uitrekenen hoeveel procent van de elektronen een blauw foton uitzendt:
$$ \frac{1,8 \times 10^{17}}{3,12 \times10^{17}} = 0,57 = 57 \text{ %} $$Als we licht van een gloeilamp op waterstof laten schijnen, dan zal het meeste licht hier dwars doorheen schijnen. Alleen licht met specifieke frequenties zal worden geabsorbeerd. Als gevolg worden er in het spectrum van het licht een aantal zwarte lijnen zichtbaar (zie de onderstaande afbeelding). We noemen dit absorptielijnen en het bijbehorende spectrum noemen we een absorptiespectrum.

Het geabsorbeerd licht wordt later in willekeurige richting weer worden uitgezonden. Het spectrum van dit licht is hieronder afgebeeld. We noemen dit een emissiespectrum en de lijnen worden spectraallijnen genoemd. Zoals verwacht vinden we in dit spectrum alleen de frequenties licht die geabsorbeerd waren uit de lichtbron.

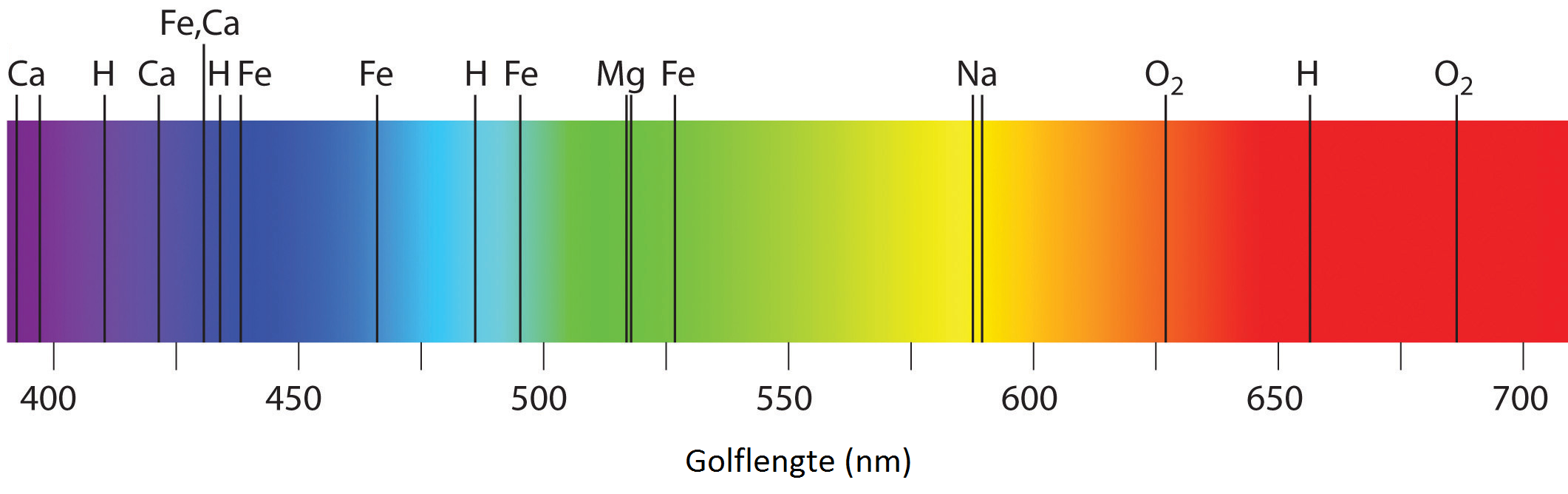
Elke stof heeft zijn eigen unieke spectrum van spectraallijnen. Als gevolg kunnen we aan de hand van het spectrum achterhalen door welke stoffen licht geschenen is. Deze techniek wordt bijvoorbeeld gebruikt om te achterhalen uit welke stof de zon of de sterren bestaan. In de kern van de zon wordt met behulp van kernfusie een continu spectrum aan licht geproduceerd. Als dit licht zich echter door de zon naar buiten werkt, worden een aantal frequenties geabsorbeerd. Hierdoor ontstaan spectraallijnen in het zonnespectrum. We noemen deze lijnen de Fraunhoferlijnen. Hieronder zien we de meest prominente absorptielijnen in het visuele gedeelte van het spectrum van de zon.
- Bereken hoeveel minuten het duurt, voordat zonlicht de aarde bereikt.
- Bij een ruimtereis naar de maan is een reflector geplaatst op het maanoppervlak. Door een laser vanaf de aarde naar deze reflector te schieten, kan de afstand tot de maan gemeten worden. Het laserlicht doet er 2560 ms over totdat het terug is op aarde. Bereken hiermee de afstand tot de maan.
- Telefonie werkt met behulp van radiosignalen. Wat is de snelheid van deze radiosignalen.
-
Sommige schepen hebben een radarinstallatie om de afstand tot andere schepen of voorwerpen in de omgeving te meten. Een radarinstallatie zendt hiervoor elektromagnetische signalen uit die weerkaatst worden door een voorwerp. Door de tijd tussen het uitzenden en het ontvangen van een signaal te meten, kan de afstand tot het voorwerp bepaald worden, ook als dat voorwerp zich op grote afstand van het schip bevindt. Een veelgebruikt type radar is de pulsradar. Dit type radar zendt een kort elektromagnetisch signaal uit en ontvangt even later de echo van dit signaal. Op een bepaald moment wordt er 0,26 ms gemeten tussen het uitzenden en het ontvangen van een signaal.
- Bereken de afstand tot het voorwerp.
- Het signaal is een puls die bestaat uit een aantal opeenvolgende elektromagnetische golven. Deze golven worden gemaakt met een vaste frequentie van 9,38 GHz. Eén puls duurt 0,100 µs. Bereken uit hoeveel golven één puls bestaat.
- Details met afmetingen van 10% van de golflengte zijn door de pulsradar net waar te nemen. Bereken de minimale afmeting van een voorwerp dat met deze pulsradar waar te nemen is.
-
Twee satellieten Grace A en B draaien achter elkaar aan om de aarde. Ze zijn een afstand van 220 km van elkaar verwijderd.
- Bereken hoe lang het duurt om een radiosignaal van de ene naar de andere satelliet te sturen.
- Grace A ontvangt continu een signaal van Grace B. De frequentie van de gebruikte radiosignalen bedraagt 32,7 GHz. Bereken de golflengte van het signaal.
- (V) Het signaal van Grace A wordt in Grace B vergeleken met een eigen referentiesignaal van dezelfde frequentie. Als de afstand AB niet verandert, dan lopen deze twee signalen in fase. De frequentie van de gebruikte radiosignalen bedraagt 32,7 GHz. Als de afstand AB groter wordt, ontstaat een faseverschil tussen het ontvangen signaal en het referentiesignaal. Op een gegeven moment is het faseverschil gelijk aan 0,015. Bereken het verschil in afstand AB bij dit faseverschil.
- In het spectrum van natrium zijn twee duidelijke absorptielijnen te zien. De eerste lijn wordt veroorzaakt door fotonen met een golflengte van 589,0 nm en de andere door fotonen met een golflengte van 589,6 nm. Laat met behulp van BINAS zien welke kleur deze fotonen hebben.
-
In de onderstaande afbeelding is het spectrum van een ster weergegeven:
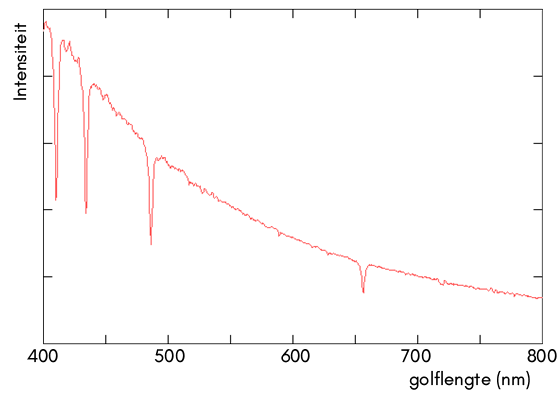
- Leg uit of het hier gaat om een absorptie- of een emissiespectrum.
- Leg uit hoe de spectraallijnen in deze ster ontstaan zijn.
- De vier zichtbare spectraallijnen worden allemaal veroorzaakt door hetzelfde element. Ga met behulp van BINAS na om welk element het hier gaat.
-
In de onderstaande afbeelding is het spectrum van een nevel weergegeven waaruit sterren zich kunnen vormen:
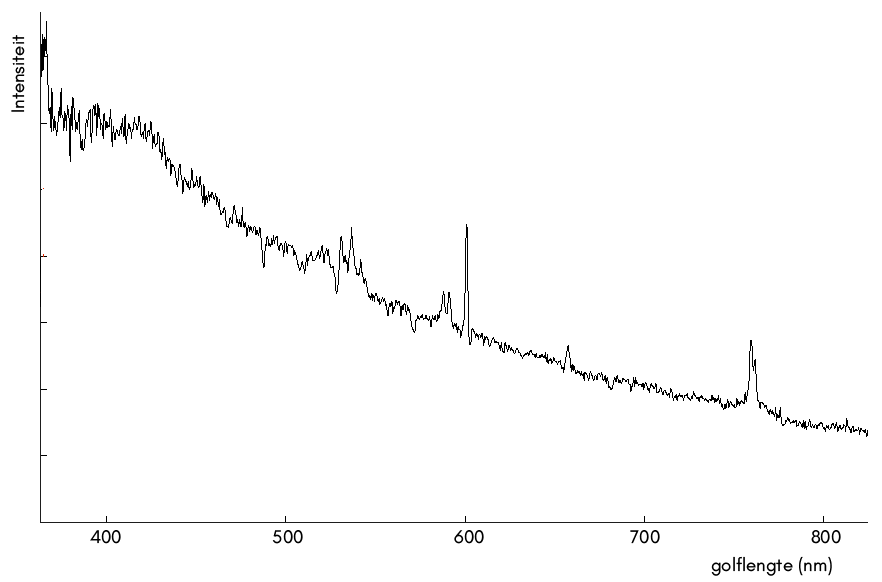
- Leg uit of het hier gaat om een absorptie- of een emissiespectrum.
- Leg uit hoe de spectraallijnen in deze nevel ontstaan zijn.
- Leg uit hoe je kan zien dat in deze nevel geen waterstof aanwezig is.
-
Een stilstaand elektron absorbeert een foton met een golflengte van 500 nm.
- Bereken de energie van het foton.
- Bereken de snelheid die het elektron hierdoor zal krijgen.
- Elk deeltje heeft zijn eigen anti-deeltje. Het anti-deeltje van het elektron is bijvoorbeeld het positron. Dit deeltje heeft exact dezelfde eigenschappen als het elektron, maar dan met een positieve lading. Als een elektron tegen een positron botst, dan worden beide deeltjes omgezet in twee dezelfde fotonen. De energie van deze fotonen is te berekenen met: $$ E = mc^2 $$ Bereken de frequentie van deze fotonen.
- Als geleidingselektronen door de LED stromen, botsen ze tegen de atomen in de LED. Als gevolg wordt blauw licht uitgezonden met een golflengte van 470 nm. Het totale vermogen aan uitgezonden licht gelijk is aan 0,075 W. Door een LED loopt een stroomsterkte van 50 mA. Bereken hoeveel procent van de geleidingselektronen dit blauwe licht heeft uitgezonden. (bron: examen VWO 2016-1)