In deze laatste paragraaf introduceren we de gravitatie-energie. We gaan deze energie o.a. gebruiken om uit te rekenen hoeveel energie nodig is om een voorwerp uit een gravitatieveld te laten ontsnappen.
Ook bij de gravitatiekracht hoort een energie. Deze wordt gegeven door:
| Gravitatie-energie (Eg) | joule (J) |
| Massa van het lichtste voorwerp (m) | kilogram (kg) |
| Massa van het zwaarste voorwerp (M) | kilogram (kg) |
| Gravitatieconstante (G) | 6,67 × 10-11 Nm2kg-2 |
| Baanstraal (r) | meter (m) |
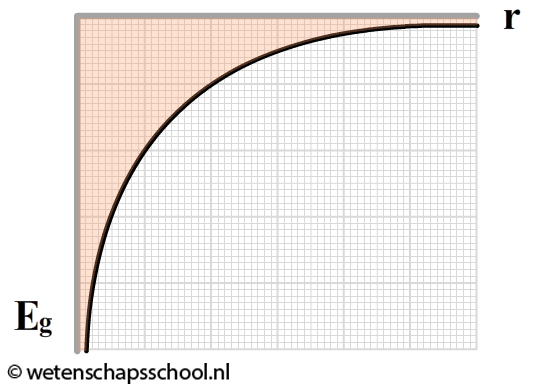
Aan deze formule kan je zien dat de gravitatie-energie altijd negatief is. Als voorwerpen zich erg ver van elkaar af bevinden, dan nadert energie de 0 joule (zie ook de onderstaande grafiek die hoort bij deze formule).
Met deze energie kunnen we o.a. de minimale snelheid uitrekenen die nodig is om een voorwerp te laten ontsnappen uit het gravitatieveld van bijvoorbeeld de aarde. We noemen deze minimale snelheid de ontsnappingssnelheid.
Als we een voorwerp wegschieten van de aarde, dan heeft het voorwerp zowel kinetische energie als gravitatie-energie (de r in de formule is bij het afschieten gelijk aan de straal van de aarde). Bij de ontsnappingssnelheid moet het voorwerp net genoeg kinetische energie meekrijgen om te ontsnappen. Deze kinetische energie wordt in zijn geheel gebruikt om te ontsnappen en als het voorwerp ver weg van de planeet is, is deze energie dus geheel opgebruikt. Op deze afstand is de gravitatie-energie ook zo goed als nul. Er geldt dus:
$$ E_{tot,begin} = E_{tot,eind} $$ $$ E_{kin,begin} + E_{g,begin} = 0 $$Nu vullen we de formules in. Let op het minteken van de gravitatie-energie:
$$ \frac{1}{2}mv_{begin}^2 -\frac{mMG}{r_{begin}} = 0 $$ $$ \frac{1}{2}mv_{begin}^2 = \frac{mMG}{r_{begin}} $$ $$ v_{begin}^2 = \frac{2MG}{r_{begin}} $$ $$ v_{begin} = \sqrt{\frac{2MG}{r}} $$De ontsnappingssnelheid is dus:
| Ontsnappingssnelheid (vontsnapping) | snelheid (m/s) |
| Massa van het zwaarste voorwerp (M) | kilogram (kg) |
| Gravitatieconstante (G) | 6,67 × 10-11 Nm2kg-2 |
| Baanstraal (r) | meter (m) |
Laten we de ontsnappingssnelheid van de aarde berekenen. We vullen voor r hier de straal van de aarde in. We vinden:
$$ \sqrt{\frac{2 \times 5,9 \times 10^{24} \times 6,7 \times 10^{-11}}{6,4 \times 10^6}} = 11 \times 10^3 \text{ m/s} $$De ontsnappingssnelheid van de aarde is dus 11 km/s.
- Een persoon wil berekenen hoe snel hij een kanonskogel omhoog zou moeten afschieten om deze te laten ontsnappen aan het gravitatieveld van de aarde. Bereken deze snelheid in km/s. Je mag de wrijvingskracht van de atmosfeer verwaarlozen.
- Een planeet beweegt in een ellipsbaan om de zon. De totale energie van een planeet in een baan om de zon bestaat uit de som van zijn kinetische energie en zijn gravitatie-energie. Beredeneer hiermee dat een planeet dichter bij de zon een grotere snelheid heeft dan op grotere afstand van de zon.
- Een terugkerende ruimtecapsule met een massa m = 5,8 × 103 kg, bevindt zich op t = 0 s op 500 km hoogte met baansnelheid van 7,5 × 103 m/s. Om veilig te landen moet de capsule in de atmosfeer energie kwijtraken. Bereken in welke orde van grootte dit energieverlies zit.
- Een komeet met een massa van 12 × 103 kg beweegt op een hoogte van 100 km boven het aardoppervlak met een snelheid van 50 km/s richting de aarde. Bij aankomst op de aarde is de massa van de komeet afgenomen tot 6,0 × 103 kg. Het totaal van de kinetische energie en de gravitatie-energie is dan nog slechts 0,20% van de oorspronkelijke totale energie. Bereken met welke snelheid de komeet op de aarde aankomt.
-
Een ruimteschip gaat in een rechte baan naar de maan.
- Neemt de gravitatie-energie van het ruimteschip tijdens de vlucht van de aarde naar de maan toe of af? Licht je antwoord toe.
- Bij het opstijgen van het ruimteschip wordt gebruik gemaakt van een stuwraket. Nadat de stuwraket op een hoogte van 300 km boven het aardoppervlak wordt afgeworpen, moet het ruimteschip voldoende snelheid hebben om de maan te bereiken. De massa van het ruimteschip is 4,0 x 103 kg. Bereken de orde van grootte van de minimale kinetische energie die het ruimteschip moet hebben op het moment van het afwerpen van de stuwraket om de maan te kunnen bereiken. De gravitatiekracht van de maan op de maanraket is te verwaarlozen ten opzichte van de kracht van de aarde.
-
Een communicatiesatelliet wordt met behulp van een raket in een geostationaire baan rond de aarde gebracht. Deze banen bevinden zich op een hoogte van 35,8 x 103 km boven het aardoppervlak. De satelliet beweegt hier met een snelheid van 3,1 x 103 m/s in zijn baan. De massa van de satelliet is 3,90 x 103 kg.
- Bereken de arbeid die de gravitatiekracht verricht als de satelliet vanaf de aarde naar zijn baan gebracht wordt.
- Om het gemakkelijker te maken om deze arbeid te verrichten, wordt gebruik gemaakt van de draaiing van de aarde om zijn eigen as. Bereken de kinetische energie van de satelliet op de evenaar door de draaiing van de aarde.
- Bereken hoeveel arbeid er dan nog minimaal door de motorkracht verricht moet worden.
-
De verkenner Pioneer-10 werd gelanceerd in 1972 en was in 1983 het eerste ruimtevaartuig dat ons zonnestelsel verliet. In 1983 bewoog Pioneer-10 met een snelheid van ongeveer 2,6 AE per jaar in de richting van de rode ster Aldebaran.
- Bereken hoeveel jaar Pioneer-10 over zijn reis naar Aldebaran zal doen als hij zijn hele reis met de gegeven snelheid beweegt.
- In het begin van de reis wordt Pioneer-10 door de zon vertraagd. Aan het eind van zijn reis wordt Pioneer-10 door Aldebaran versneld. Tim en Maaike bespreken het effect hiervan op de gemiddelde snelheid van Pioneer-10. Tim denkt dat de gemiddelde snelheid minder dan 2,6 AE per jaar is door de invloed van de zon. Maaike meent dat de gemiddelde snelheid meer dan 2,6 AE per jaar is, omdat de massa van Aldebaran 25 keer zo groot is als de massa van de zon. Leg uit wie er gelijk heeft.
- In 1983 bevond Pioneer-10 zich op een afstand r = 6,2 x 1012 m van de zon. Toon aan dat zijn snelheid dan ruimschoots voldoende is om uit het zonnestelsel te ontsnappen.
 Rekenen met de gravitatie-energie en de ontsnappingssnelheid
Rekenen met de gravitatie-energie en de ontsnappingssnelheid