In deze paragraaf gaan we de begrippen spanning en stroomsterkte gebruiken om te rekenen met verschillende soorten schakelingen.

Laten we eens kijken hoe het zit met de stroomsterkte in een aantal verschillende schakelingen. In de onderstaande animatie zien we lading stromen door een serieschakeling. In een serieschakeling gaat alle lading door alle lampjes heen. De hoeveelheid lading die uit de spanningsbron stroomt is dus gelijk aan de hoeveelheid lading die het rechter lampje in stroomt en even later het linker lampje in stroomt. De stroomsterkte is in een serieschakeling dus in alle onderdelen gelijk.

In een parallelschakeling zijn er meerdere stroomkringen waarover de lading zich verdeelt. Hoe de stroomsterkte zich verdeelt hangt af van de weerstand van de lampjes. Alleen als de lampjes dezelfde weerstand hebben, zal de stroomsterkte door beide lampjes gelijk zijn.

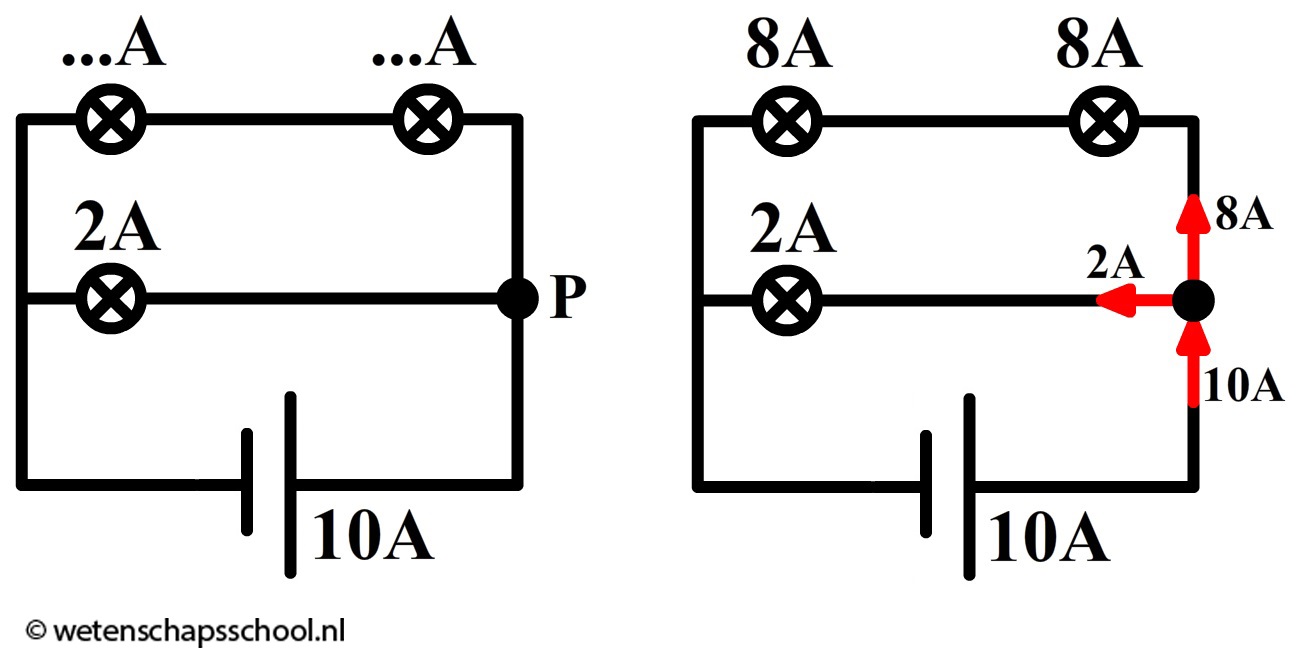
Laten we nu een gemengde schakeling bestuderen. Hieronder zien we 4 A uit de spanningsbron stromen. Al deze lading komt aan bij de rechter lamp. Hier is de stroomsterkte dus ook 4 A. Daarna splitsen de ladingen op. Stel dat 1 A bovenlangs gaat, dan weet je dat de rest (3 A) onderlangs moet gaan.

In de onderstaande afbeelding stroomt 10 A uit de spanningsbron. Bij punt P splitsen de ladingen op. Als blijkt dat 2 A linksaf gaat, dan moet de rest (8 A) dus bovenlangs gaan. Deze 8 A gaat door beide bovenstaande lampjes heen. Door elk stroomt dus 8 A.

Klas 4

We kunnen deze ideeën ook wiskundig samenvatten met behulp van de zogenaamde stroomwet van Kirchhoff. In het bovenstaande voorbeeld zien we dat de stroomsterkte die naar punt P stroomt gelijk is aan de stroomsterkte die van punt P wegstroomt. Wiskundig schrijven we dit als:

$$ \sum I_{in} = \sum I_{uit} $$

Som van toestromende stroomsterktes (ΣI_in)	ampère (A)
Som van wegstromende stroomsterktes (ΣI_uit)	ampère (A)

Als we stromen die naar een knooppunt toe gaan positief noemen en stromen die van een knooppunt af gaan negatief, dan kunnen we deze formule nog simpeler opschrijven:

$$ \sum I = 0 $$

Som van stroomsterktes (ΣI)

ampère (A)

Laten we nu de spanning bestuderen. Hieronder zien we bijvoorbeeld een serieschakeling. Stel dat de spanningsbron een spanning van 20 V heeft, dan betekent dit dat elke coulomb aan lading 20 J aan energie meekrijgt om te besteden in de schakeling. Elke lading gaat in deze schakeling door beide lampjes heen. Als gevolg moet elke lading zijn energie verdelen over de twee lampjes. De 20 V aan spanning wordt dus verdeeld over de lampjes. Hoe de spanning precies verdeeld wordt hangt af van de weerstand van de lampjes. Alleen als de lampjes dezelfde weerstand hebben, zal de spanning over beide lampjes gelijk zijn.

In een parallelschakeling gaat een enkele lading maar door één lampje heen. Elke lading besteed dus al zijn energie in slechts één lampje. Als de spanningsbron een spanning van 20 V heeft, dan heeft in een parallelschakeling elk lampje dus ook een spanning van 20 V. Het veranderen van de weerstanden heeft hier geen invloed op.

Nu tijd voor gemengde schakelingen. De onderstaande schakeling bestaat uit twee stroomkringen (in rood aangegeven). Sommige ladingen gaan door de ene stroomkring en sommige ladingen gaan door de andere stroomkring. In elke stroomkring moet een coulomb aan lading in totaal 12 J kwijtraken. Als gegeven is dat over rechter lamp een spanning van 8 V staat, dan moet over de twee linker lampen dus elk een spanning van 4 V staan. Op deze manier wordt in elke stroomkring 12 J aan energie besteed. Voor elke stroomkring geldt dus dat de spanning van de spanningsbron gelijk is aan de spanning van de onderdelen in deze stroomkring tezamen.

Klas 4

We kunnen deze ideeën ook wiskundig samenvatten met behulp van de zogenaamde spanningswet van Kirchhoff:

$$ U_{bron} = \sum U $$ $$ (\text{voor elke stroomkring})$$

Spanning van spanningsbron (U_bron)	volt (V)
Som van spanningen in stroomkring (ΣU)	volt (V)

Als we bij een afname van de spanning afspreken dat de spanning negatief is en bij een toename van de spanning afspreken dat de spanning positief is, dan kunnen we deze formule nog simpeler schrijven als:

$$ \sum U = 0 $$

Som van spanningen in stroomkring (ΣU)

volt (V)

4 VWO

In de onderstaande voorbeeld passen we de wet van Kirchhoff in een ingewikkeldere schakeling toe. Bedoeling is om de spanning van U₁ en U₂ te berekenen. De pijlen in de afbeelding geven de stroomrichting aan.

Laten we eerst naar stroomkring F-A-B-E kijken. De wet van Kirchhoff wordt hier:

$$ U_A + U_1 + U_2 + U_B = 0 $$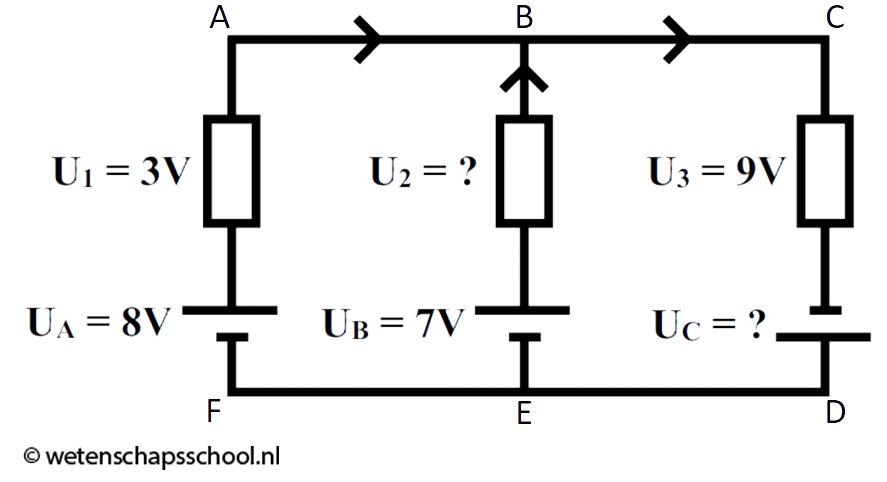

Als we de stroomkring vanaf punt F volgen, dan komen we eerst een spanningsbron van 8 V tegen. Omdat de spanning hier van min naar plus loopt, zorgt dit voor een positieve spanning in de wet van Kirchhoff. Door de weerstand die daarop volgt hebben we een negatieve spanning van 3 V. De spanning is negatief, omdat de spanning door deze weerstand heen afneemt. Dan komen we nog een weerstand tegen met een onbekende spanning. We zien hier al dat de spanning positief moet zijn, omdat we hier tegen de stroom in gaan. De stroomkring eindigt met nog een spanningsbron. We vinden hier een negatieve waarde, omdat we van de plus naar de min bewegen. Er geldt dus:

$$ 8 + (-3) + U_2 + (-7) = 0 $$ $$ U_2 = +2 \text{ V} $$

In de opdrachten gaan we ook stroomkring F-A-C-D bestuderen.

Training

Rekenen met stroomsterkte en spanning in serie-, parallel- en gemengde schakelingen.

(2,3,4) Klik op de lampjes en de spanningsbron en vul de juiste stroomsterkte en spanning in:
(2,3,4) Beschrijf in woorden hoe je kan rekenen met stroomsterkte en spanning in gemengde schakelingen.
(2,3,4) Twee dezelfde lampjes zijn in serie aangesloten op een batterij. De batterij levert een stroomsterkte van 250 mA. Leg uit hoe groot de stroomsterkte in elk van de lampjes is.
(2,3,4) Twee dezelfde lampjes zijn parallel aangesloten op een batterij. De batterij levert een stroomsterkte van 0,090 A. Leg uit hoe groot de stroomsterkte in elk van de lampjes is.
(2,3) Bij sommige kerstverlichting gaan alle lampjes uit als we één lampje loshalen. Leg aan de hand van deze observatie uit of kerstverlichting uit een serie- of een parallelschakeling bestaat.
(2,3) Als je thuis de stekker van één lamp uit een stopcontact haalt, gaan gelukkig niet alle lampen in het huis plotseling uit. Leg aan de hand van deze observatie uit of de schakeling waarop de stopcontacten in huis zijn aangesloten een serie- of een parallelschakeling is.
(2,3,4) Verklaar de volgende correcte uitspraken met behulp van het begrip spanning.
1. De spanning is overal gelijk in een parallelschakeling.
2. De spanning wordt verdeeld over de lampjes in een serieschakeling.
(2,3,4) Hieronder zien we drie schakelingen. In elke schakeling wordt hetzelfde type lampje gebruikt.
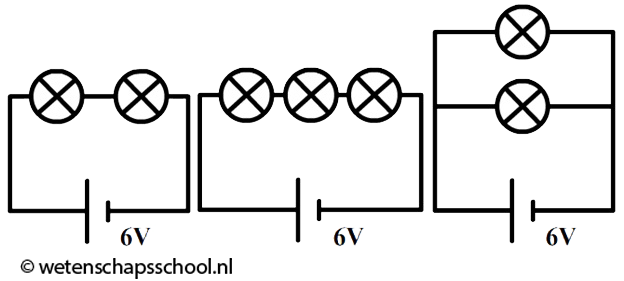
1. Reken de spanning over elk lampje in deze schakelingen uit.
2. Leg uit in welke schakeling de stroomsterkte door de lampjes het kleinst is en in welke het grootst.
3. Leg met behulp van de begrippen stroomsterkte en spanning uit in welke schakeling de lampjes het felst branden.
(2,3,4) Hieronder zien we twee schakelingen met een aantal dezelfde lampjes:
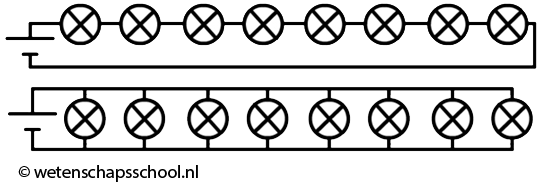
1. Beschrijf wat er gebeurt als een lampje in de bovenste schakeling doorbrandt.
2. Beschrijf wat er gebeurt als een lampje in de onderste schakeling doorbrandt.
3. Leg uit of de spanning over de lampjes verandert als we een lampje uit de onderste schakeling verwijderen.
(2,3,4) In de volgende schakeling zijn vijf dezelfde lampjes opgenomen.
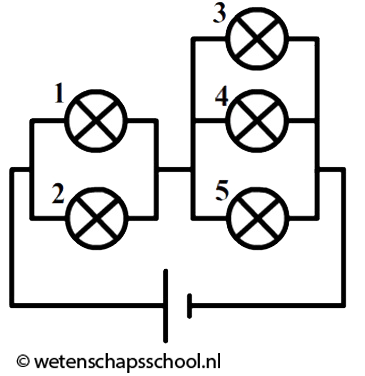
1. Door welke lampjes in de bovenste schakeling is de stroomsterkte het grootst? Leg je keuze uit.
2. Door lampje 1 en 2 stroomt elk 750 mA. Bereken de totale stroomsterkte die de spanningsbron levert.
3. Bereken de stroomsterkte door lamp 3.
4. Over lampje 1 en 2 staat elk een spanning van 6,0 V en over lampjes 3, 4 en 5 staat elk een spanning van 4,0 V. Bereken de spanning over de spanningsbron.
(2,3,4) In een koplamp van een fiets zitten drie lampjes, die ieder op een spanning van 4,5 V branden. De spanning wordt geleverd door drie batterijen, die ieder een spanning leveren van 1,5 V. Teken de schakeling die hier beschreven is.

Rekenen met de wetten van Kirchhoff

(4V) Bereken met de wet van Kirchhoff de waarde van U₁ en U₂ in de onderstaande schakeling. De pijlen in de afbeelding geven de stroomrichting aan.