In deze paragraaf beginnen we met het begrijpen van de satellietbaan met behulp van een gedachtenexperiment van Newton. Daarna bespreken we de relevante formules als het gaat om cirkelbanen in de ruimte. Hiermee kunnen we o.a. de massa van de zon bepalen.

Voor Newton's ontdekkingen, dachten wetenschappers dat de natuurwetten op aarde anders waren dan de natuurwetten in de ruimte. In de ruimte zien we objecten namelijk vaak in cirkelbanen bewegen, terwijl dit op aarde slechts zelden gebeurt. Newton liet echter zien dat met dezelfde formule zowel het vallen van voorwerpen op aarde als de planeetbanen verklaard konden worden. Newton's redenering was als volgt. Stel dat we een gigantisch kanon op aarde zouden bouwen (zie de onderstaande animatie), dan moet het mogelijk zijn om de kogel zo snel af te schieten dat de valbeweging van de kanonskogel dezelfde bocht maakt als de kromming van de aarde. In dat geval zou de kogel altijd vallen, maar nooit dichter bij de aarde komen. De kogel zal dan in een baan om de aarde bewegen, zoals ook de maan dat doet. Newton liet hiermee zien dat hij met de zwaartekracht de baan van de maan kon verklaren!

Newton begreep ook dat alle voorwerpen in het universum elkaar aantrekken doormiddel van de gravitatiekracht. De gravitatiekracht is een ander woord voor de zwaartekracht, maar meestal gebruiken we het woord 'zwaartekracht' voor het beschrijven van vallende voorwerpen op aarde en het woord 'gravitatiekracht' voor het beschrijven van de beweging van hemellichamen. In de extra paragraaf in dit hoofdstuk zullen we bewijzen dat deze kracht gegeven wordt door:

$$ F_g = \frac{GMm}{r^2} $$
Gravitatiekracht (Fg) newton (N)
Gravitatieconstante (G) 6,67 × 10-11 Nm2kg-2
Grootste massa (M) kilogram (kg)
Kleinste massa (m) kilogram (kg)
Afstand tussen de massamiddelpunten (r) meter (m)

Als we deze formule gelijkstellen aan de al bekende formule \(F_z = mg \), dan vinden we:

$$ mg = \frac{GMm}{r^2} $$

Als we de massa m aan beide kanten wegstrepen, dan vinden we dat de valversnelling g te berekenen is met:

$$ g = \frac{GM}{r^2} $$
Valversnelling (g) meter per seconde per seconde (m/s2)
Grootste massa (M) kilogram (kg)
Gravitatieconstante (G) 6,67 × 10-11 Nm2kg-2
Afstand tussen de massamiddelpunten (r) meter (m)

Met deze formule kunnen we de massa van de aarde bepalen. We schrijven de formule eerst als volgt om:

$$ M = \frac{gr^2}{G} $$

We vinden:

$$ M = \frac{9,81 \times (6,371\times 10^6)^2}{6,67 \times 10^{-11}} = 5,98 \times 10^{24} \text{ kg}$$

De massa van de aarde is dus 5,98 × 1024 kg.

Omgekeerd kan de formule nu ook worden gebruikt om g uit te rekenen op een willekeurige afstand van de aarde. Op het aardoppervlak vinden we natuurlijk de vertrouwde waarde 9,81 m/s2:

$$ g = \frac{GM}{r^2} $$ $$ g = \frac{5,98 \times 10^{24} \times 6,67 \times 10^{-11}}{(6,371\times 10^6)^2} = 9,81 \text{ m/s}^2 $$

Als een object een cirkelbaan maakt om bijvoorbeeld de aarde, dan weten we dat er een middelpuntzoekende kracht werkt die geleverd wordt door de gravitatiekracht. In dit geval geldt dus:

$$ F_{mpz} = F_g $$ $$ \frac{mv^2}{r} = \frac{GMm}{r^2} $$

We kunnen hier aan beide kanten een m en een r wegstrepen en daarna kunnen we de formule herschrijven tot:

$$ v_{baan} = \sqrt{\frac{GM}{r}} $$
Baansnelheid (vbaan) meter per seconde (m/s)
Gravitatieconstante (G) 6,67 × 10-11 Nm2kg-2
Grootste massa (M) kilogram (kg)
Baanstraal (r) meter (m)

Klas 4

Voor de baansnelheid geldt \( v_{baan} = 2\pi r/T \). Als we deze twee formules combineren, dan vinden we:

$$ \left( \frac{2\pi r}{T} \right)^2 = \frac{GM}{r} $$

Dit kunnen we herschrijven tot:

$$ \frac{ r^3}{T^2} = \frac{GM}{4\pi^2} $$
Omlooptijd (T) seconde (s)
Gravitatieconstante (G) 6,67 × 10-11 Nm2kg-2
Grootste massa (M) kilogram (kg)
Baanstraal (r) meter (m)

Deze formule wordt de derde wet van Kepler genoemd.

Laten we de derde wet van Kepler eens toepassen op het bewegen van de aarde om de zon. Met deze formule kunnen we de massa van de zon uitrekenen! Het enige dat we nodig hebben is de afstand van de aarde tot de zon (149,6×109m) en de omlooptijd van de aarde (365 dagen):

$$ M = \frac{4\pi^2 r^3}{GT^2}$$ $$ M = \frac{4\pi^2 (149,6 \times 10^9)^3}{6,67 \times 10^{-11} \times (365 \times 24 \times 60 \times 60)^2} = 1,99 \times 10^{30} \text{ kg} $$

We kunnen deze formule ook gebruiken om de omlooptijden van satellieten om de aarde uit te rekenen. Het internationale ruimtestation (ISS) bevindt zich bijvoorbeeld 300 km boven het aardoppervlak. De afstand r van het centrum van de aarde tot de satelliet is dus:

$$ r = 6,37 \times 10^6 + 300 \times 10^3 = 6,67 \times 10^6 \text{ m} $$

Nu kunnen we de omlooptijd uitrekenen:

$$ T = \sqrt{\frac{4\pi^2}{GM_{aarde}} r^3} $$ $$ T = \sqrt{\frac{4\pi^2}{6,67 \times 10^{-11} \times 5,97 \times 10^{24} } (6,67 \times 10^6)^3} = 5,42 \times 10^3 \text{ s} $$

Dit is slechts anderhalf uur!






Training
    Rekenen met de algemene gravitatiewet
  1. Laat met behulp van de formule van de gravitatiekracht zien dat de eenheid van G geschreven kan worden als Nm2kg-2 en als m3kg-1s-2.
  2. Cavendish bepaalde de constante G door de kracht te meten tussen een loden bol met een massa van 7,3 kg een andere loden bol met een massa van 158 kg. De zwaartepunten van de bollen werden op een afstand van 250 mm van elkaar opgehangen. De kracht die Cavendish mat was gelijk aan 1,23 × 10-6 N. Bereken hiermee de constante G.
  3. Bereken de gravitatiekracht werkende op een persoon van 80 kg in het internationaal ruimtestation (400 km boven het aardoppervlak).
  4. Hieronder zien we de baan van de satelliet WMAP. De satelliet heeft een massa van 840 kg en bevindt zich op 1,5 miljoen kilometer afstand van de aarde. De baan van WMAP is zo gemaakt dat deze precies meedraait met de aarde. De zon, de aarde en WMAP blijven dus op één lijn liggen.
    1. Laat zien dat de middelpuntzoekende kracht die werkt op WMAP gelijk moet zijn aan 5,0 N om hem in deze baan te houden.
    2. Deze kracht wordt geleverd door de zwaartekracht van de aarde en de zon tezamen. Ga na welke van de twee gravitatiekrachten hieraan de grootste bijdrage levert.
    (bron: examen VWO 2015-pilot)
    5. Rekenen met de wet van Kepler, de formule voor de baansnelheid en de formule voor de valversnelling
  5. (V) Leid de wet van Kepler af.
  6. In deze opdracht bestuderen we twee manieren waarop de massa van de maan gemeten is.
    1. In 1966 lukte het de Russen voor het eerst om het ruimtevaartuig Luna 10 in een baan om de maan te krijgen. Luna 10 bevond zich 682 km boven het maanoppervlak en de omlooptijd was 178 minuten. Gebruik deze data om de massa van de maan uit te rekenen. Kijk daarna in BINAS of je de juist waarde gevonden hebt.
    2. In 1969 lukte het de Amerikanen om op de maan te landen. Ze vonden dat op het oppervlak van de maan de valversnelling gelijk was aan 1,62 m/s2. Gebruik ook deze waarde om de massa van de maan te vinden.
  7. Wat is de omlooptijd van geostationaire satellieten?
  8. (V) Geostationaire satellieten zijn satellieten die meedraaien met de rotatie van de aarde om zijn eigen as. Bereken op welke hoogte boven het aardoppervlak deze satellieten geplaatst moeten worden.
  9. De maan Oberon van Uranus heeft een omlooptijd van 13,5 dagen. De afstand van Uranus tot zijn maan is 5,826 × 105 km. Bereken hiermee de massa van Uranus. Kijk daarna wederom in BINAS om te kijken of je de juiste waarde gevonden hebt.
  10. In de koude oorlog wilden de Amerikanen zo veel mogelijk te weten komen over de satellieten van de Russen. De snelheid van de satellieten en de hoogte van de satellieten boven het aardoppervlak kon men snel achterhalen. Het vinden van de massa van de satellieten bleek echter niet mogelijk. Laat aan de hand van een berekening zien dat de massa geen invloed heeft op de beweging van de satelliet en dus ook niet te meten is.
  11. (V) Een satelliet die door de buitenste lagen van de atmosfeer rondcirkelt, ondervindt een kleine wrijvingskracht. Als hij geen aandrijfmotor heeft, zal hij daardoor in een steeds lagere baan rond de aarde gaan cirkelen en uiteindelijk op de aarde neerstorten (zie de onderstaande grafiek).

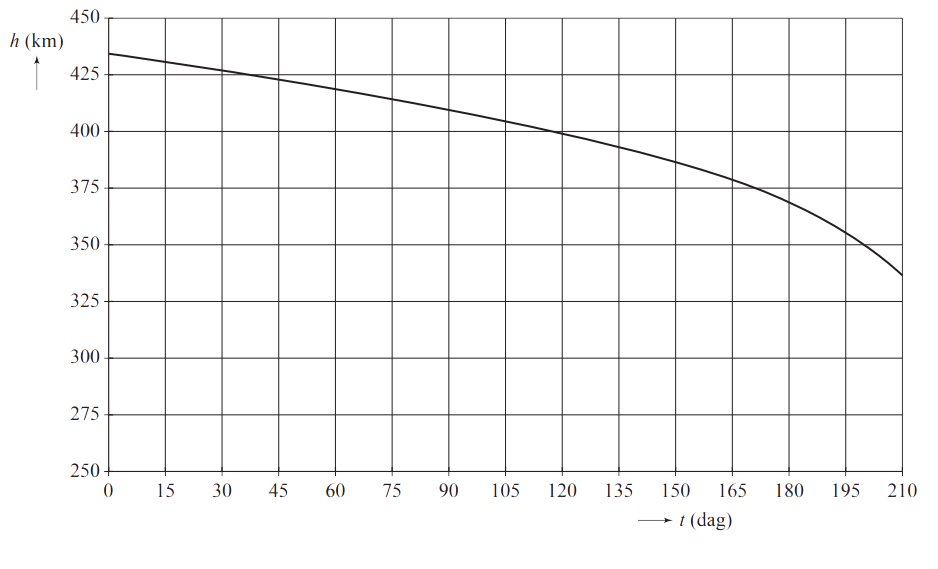    Op een bepaald moment bevindt de satelliet zich op een hoogte van 400 km boven de aarde. Bepaal op dit moment het hoogteverlies per omwenteling om de aarde. Bereken hiervoor eerst hoe lang een omwenteling op deze hoogte duurt.
    (bron: examen VWO 2011-2)
  12. (V) De ringen van Saturnus bestaan uit vele kleine ijs- en rotsblokken die in een baan om Saturnus bewegen.
    1. Laat met een formule zien dat de deeltjes in de ring dicht bij Saturnus de deeltjes verder weg telkens inhalen.
    2. In veel gevallen zouden deze ijs- en rotsblokjes door de zwaartekracht samentrekken en een maan vormen. De zwaartekracht van Saturnus maakt dit echter onmogelijk. In deze opdracht gaan we begrijpen waarom.
      Hieronder zien we bijvoorbeeld zo'n rotsblok. Omdat het rotsblok in een cirkel om Saturnus draait, weten we dat de gravitatiekracht die in het massamiddelpunt van het rotsblok werkt gelijk is aan de middelpuntzoekende kracht (zie de onderstaande afbeelding).

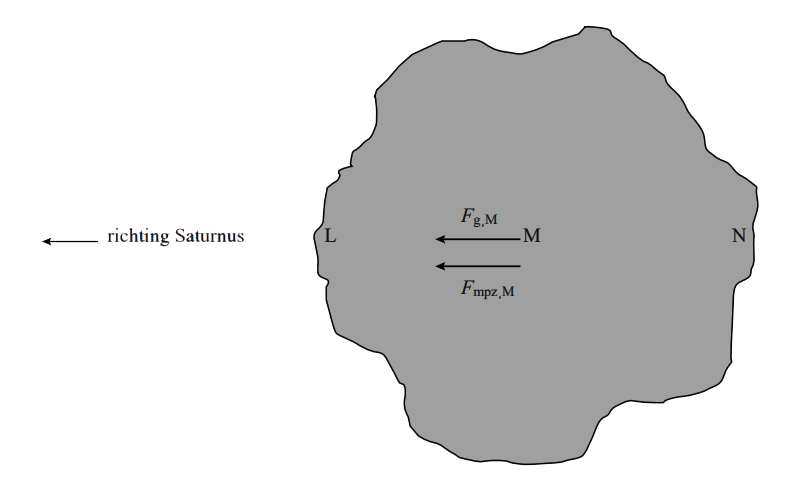      Op positie L en N in de afbeelding is de gravitatiekracht echter niet gelijk aan de middelpuntzoekende kracht. Laat zien dat de gravitatiekracht op punt L groter is dan de middelpuntzoekende kracht en dat op punt N de middelpuntzoekende kracht groter is dan de gravitatiekracht. Leg hiermee uit dat Saturnus met deze krachten de steen uit elkaar probeert te trekken.
    3. In verticale richting wordt de steen juist in elkaar gedrukt. Laat met behulp van een tekening van krachten zien waarom dit gebeurt.
    (bron: examen VWO 2012-pilot)
  13. (V) De valversnelling is niet overal op aarde precies gelijk. Dit komt o.a. door de aanwezigheid van bergen. Om deze variaties te meten zijn twee satellieten, GRACE A en GRACE B, gelanceerd. De twee satellieten draaien achter elkaar aan om de aarde op een hoogte van 485 km met een onderlinge afstand van normaal gesproken 220 km. Kleine afwijkingen in de zwaartekracht beïnvloeden de onderlinge afstand tussen de satellieten.
    1. Laat met een berekening zien dat de satellieten per etmaal 15 rondjes maken om de aarde.
    2. Hieronder zien we GRACE A en B over een gebergte bewegen. Leg uit dat de berg ervoor zorgt dat de afstand tussen A en B eerst iets groter wordt en daarna weer de oorspronkelijke waarde aanneemt.
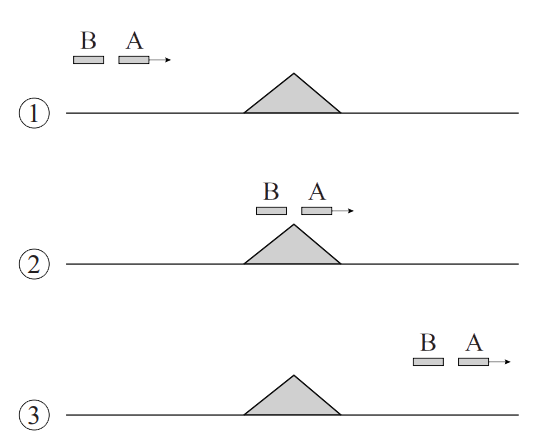
    3. Op een gegeven moment bewegen de twee GRACE satellieten over de Himalaya. De Himalaya wordt in de afbeelding aangegeven als een massa MH. In de getekende positie ondervinden beide satellieten elk een (zeer kleine) extra versnelling aH door de gravitatiekracht van MH.

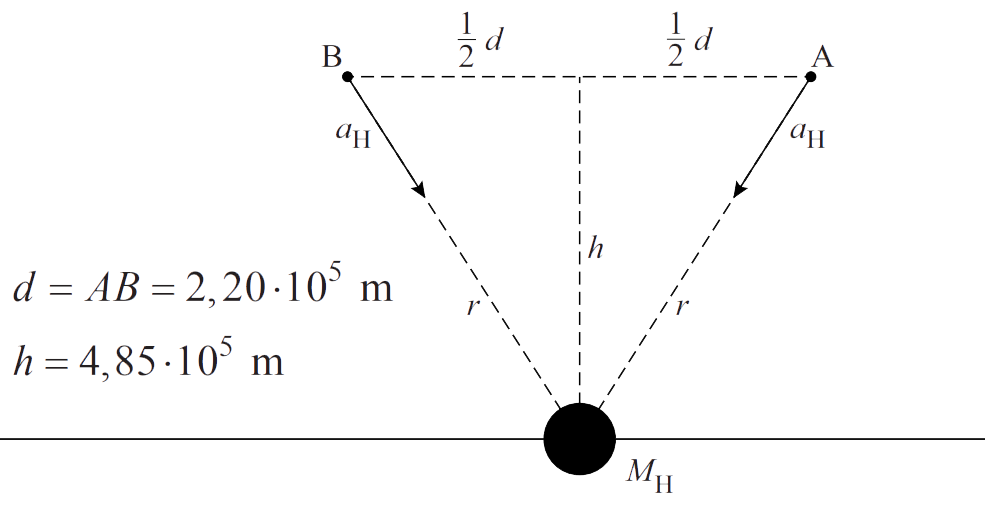      Voor de grootte van de onderlinge (relatieve) versnelling in de x-richting tussen de twee satellieten geldt: $$ a_{rel,x} = GM_1\frac{d}{r^3} $$ Toon dit aan.
    4. In de onderstaande afbeelding is de onderlinge versnelling uitgezet tegen de tijd voor de beweging over de Himalaya: Bepaal met dit figuur de massa van de Himalaya.
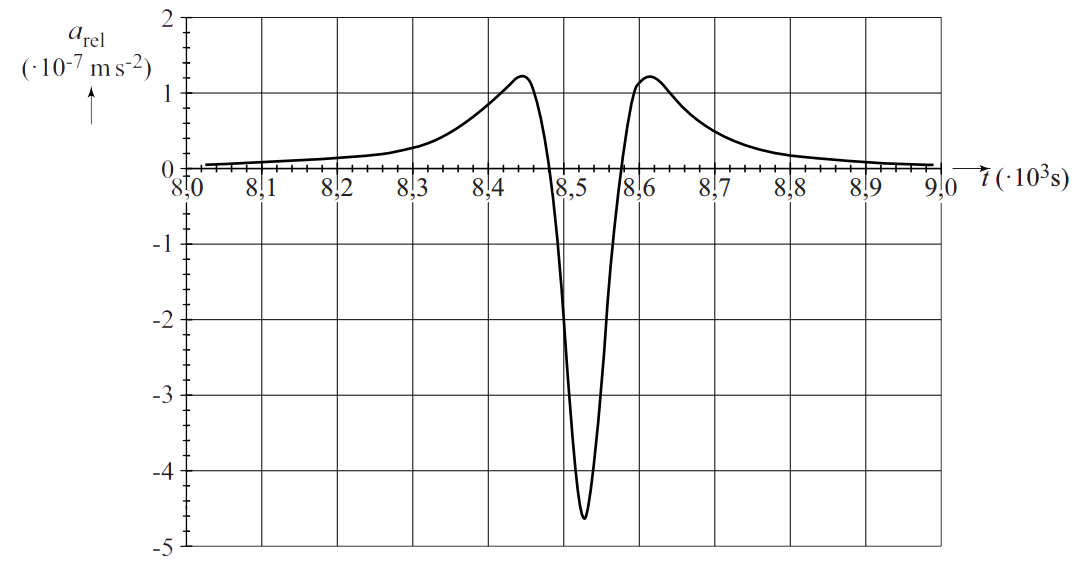      5. (bron: examen VWO 2013-pilot)