In deze paragraaf kijken we nogmaals terug naar het begrip gewicht en gewichtloosheid (zoals we ook in het hoofdstuk 'kracht' gedaan hebben). Deze keer passen we het toe op de cirkelbeweging. We gaan hiermee begrijpen waarom voorwerpen in een baan om de aarde gewichtloosheid ervaren.

De middelpuntzoekende kracht kan ervoor zorgen dat een persoon gewichtloosheid ervaart. Dit kunnen we begrijpen met het volgende voorbeeld. In de onderstaande afbeelding zien we een achtbaankarretje dat een bocht maakt. Als de kar stil zou staan boven op deze bocht, dan zou een persoon in dit karretje met zijn volledige zwaartekracht tegen zijn stoel drukken. Als het karretje met een behoorlijke snelheid deze bocht maakt, dan is er een middelpuntzoekende kracht nodig om de persoon in zijn baan te houden. Deze kracht wordt geleverd door de zwaartekracht van de persoon. Een deel van de zwaartekracht van de persoon zal nu dus niet gebruikt worden om de persoon tegen de stoel te drukken, maar zal gebruikt worden als middelpuntzoekende kracht. Als gevolg voelt de persoon zich nu lichter.

Als de kar nog sneller gaat bewegen, dan komt er een moment dat de zwaartekracht gelijk wordt aan de middelpuntzoekende kracht. De volledige zwaartekracht wordt nu dus gebruikt als middelpuntzoekende kracht en er is dus geen kracht meer over waarmee de persoon tegen de stoel drukt. Als gevolg ervaart de persoon nu gewichtloosheid.

Hetzelfde effect vindt plaats in een satelliet in zijn baan om de aarde. We krijgen een satelliet in een baan om de aarde door het een snelheid mee te geven, waarbij de middelpuntzoekende kracht gelijk wordt aan de zwaartekracht. Als gevolg is de satelliet gewichtloos en valt hierdoor niet meer terug naar de aarde. De satelliet bevindt zich nu in een baan om de aarde.






Training
    Reken met de middelpuntzoekende kracht en gewichtloosheid.
  1. Een persoon in een achtbaankarretje gaat over de kop.

    1. De persoon gaat net snel genoeg dat de persoon op het hoogste punt even gewichtloos is. Is de middelpuntzoekende kracht nu groter dan, kleiner dan of gelijk aan de zwaartekracht? Is er nu een normaalkracht aanwezig? Zo ja, geef dan ook de richting van de normaalkracht.
    2. De persoon gaat nu sneller de looping door dan in vraag a). Is de middelpuntzoekende kracht nu groter dan, kleiner dan of gelijk aan de zwaartekracht? Is er nu een normaalkracht aanwezig? Zo ja, geef dan ook de richting van de normaalkracht.
    3. Door een storing gaat de persoon nu zo langzaam de looping door dat hij van de bodem van zijn stoel valt en nog net door de veiligheidsbeugel op zijn plek wordt gehouden. Is er nu een normaalkracht aanwezig? Zo ja, geef dan ook de richting van de normaalkracht.
    4. Een persoon van 70 kg gaat met een snelheid van 55 km/h door het hoogste punt van de looping. De straal van de looping is 12 m. Bereken de grootte van de zwaartekracht, de middelpuntzoekende kracht en de normaalkracht. Geef ook de richting van de normaalkracht.
  2. Leg uit in welke omstandigheden men gewichtloosheid ervaart bij het maken van een cirkelbeweging.
  3. Een persoon van 70 kg gaat met zijn vliegtuig over de kop. Zijn cirkelvormige baan heeft een straal van 20 meter. Hij gaat snel genoeg dat zijn stoel een normaalkracht op hem uitoefent van 200N. Bereken de snelheid waarmee het vliegtuig door zijn hoogste punt gaat.

  4. Het is ook mogelijk om als mens door een kleine looping te rennen. De looping in de onderstaande afbeelding heeft een diameter van 2,8m.


    Bereken de minimale snelheid die de persoon moet hebben om door de looping te rennen zonder te vallen. Laat hiervoor eerst zien dat:
    $$ v_{min} = \sqrt{gr} $$
  5. Een persoon van 80 kg bevindt zich op de evenaar.
    1. Laat met een berekening zien dat de middelpuntzoekende kracht die op de persoon werkt gelijk is aan 2,7 N.
    2. Hoe groot is de normaalkracht die de grond op de persoon uitoefent in dat geval?
    3. Hoe snel zou de aarde moeten draaien om de persoon gewichtloos te maken?
  6. Hieronder zien we een slinger die heen en weer beweegt. De lengte van het touw is 1,0 m, het blokje heeft een massa van 80 g en de maximale uitwijkingshoek is 30°. De afbeelding is niet op schaal weergegeven.

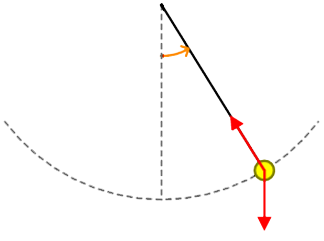
    1. Bij zijn maximale uitwijking is de middelpuntzoekende kracht die op het blokje werkt nul. Leg dit uit.
    2. Bereken de spankracht in het touw bij maximale uitwijking.
    3. Op het laagste punt werkt er zowel een spankracht als een zwaartekracht. Leg uit dat de spankracht groter moet zijn dan de zwaartekracht.
    4. De massa gaat met een snelheid van 0,2 m/s door het laagste punt. Bereken de spankracht in het touw.
  7. In de onderstaande afbeelding zien we een dubbelplanetoïde, bestaand uit twee brokstukken die om elkaar heen draaien. De grote wordt α genoemd en de kleine β.

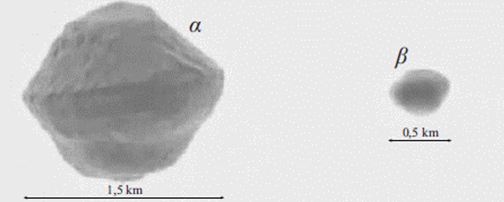    In de onderstaande tabel staan een aantal gegevens van α:
    Massa 2,6× 1012 kg
    Diameter 1,5 km
    Gravitatieversnelling op de evenaar 4,3 × 10-4 m/s2
    Rotatietijd om eigen as 2,5 h
    1. α draait zo snel dat losliggende stenen op de planetoïde lichter aanvoelen dat je met alleen de zwaartekracht zou verwachten. Leg uit hoe de draaiing van de planetoïde hiervoor zorgt.
    2. Bereken hoeveel procent een losliggende steen op α lichter aanvoelt dan je met de zwaartekracht alleen zou verwachten.
    3. Als de planetoïde nog sneller zou bewegen, dan zouden losliggende stenen zweven op het oppervlak van de planetoïde. Bij welke omlooptijd gebeurt dit?
    (bron: examen VWO 2014-pilot)