In deze paragraaf bestuderen we de kracht die nodig is om een object in een cirkelbaan te houden. We noemen dit de middelpuntzoekende kracht.

In de vorige paragraaf hebben we geleerd over cirkelbewegingen, maar hoe krijgen we een voorwerp in een cirkelbaan? Dit doen we door een kracht uit te oefenen loodrecht op de bewegingsrichting van het voorwerp. We zien dit gebeuren in de onderstaande afbeelding.

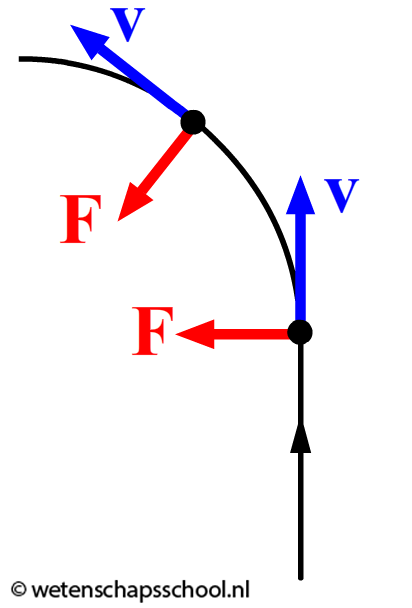
In de onderstaande animatie zien we een voorwerp dat in een cirkelbaan beweegt. Zoals je kunt zien staat er tijdens de gehele beweging een kracht loodrecht op de bewegingsrichting. Merk ook op dat deze kracht telkens naar het midden van de cirkelbaan gericht is. We noemen een dergelijke kracht daarom ook wel een middelpuntzoekende kracht (Fmpz).

We kunnen deze beweging als volgt begrijpen. Volgens de eerste wet van Newton bewegen ongehinderde voorwerpen met een constante snelheid en in een rechte lijn. We noemen dit ook wel een eenparige beweging. Een voorwerp dat een cirkelbeweging maakt, zou dus 'het liefst' op elk moment rechtdoor willen bewegen. De middelpuntzoekende kracht trekt het voorwerp echter elk moment terug richting het middelpunt van de cirkel. Op deze manier blijft het voorwerp in zijn cirkelbaan.

In de extra paragraaf aan het eind van dit hoofdstuk zullen we bewijzen dat voor het maken van een cirkelbeweging de grootte van deze kracht altijd gelijk moet zijn aan:

$$ F_{mpz} = \frac{mv_{baan}^2}{r_{baan}} \;\;\;\;\;\;\;\;\; \text{Gebruik altijd SI-eenheden}$$
Middelpuntzoekende kracht (Fmpz) newton (N)
Massa (m) kilogram (kg)
Baansnelheid (vbaan) meter per seconde (m/s)
Baanstraal (rbaan) meter (m)

Het is belangrijk om te realiseren dat de middelpuntzoekende kracht niet een 'nieuwe soort kracht' is. Het is de kracht die nodig is om een voorwerp in zijn baan te houden en dit kan in principe door elke kracht gedaan worden. Als we een steen horizontaal rondslingeren aan een touw, dan is het bijvoorbeeld de spankracht in het touw, dat er voor zorgt dat de steen in zijn baan blijft. We zeggen in dat geval de middelpuntzoekende kracht geleverd wordt door de spierkracht.

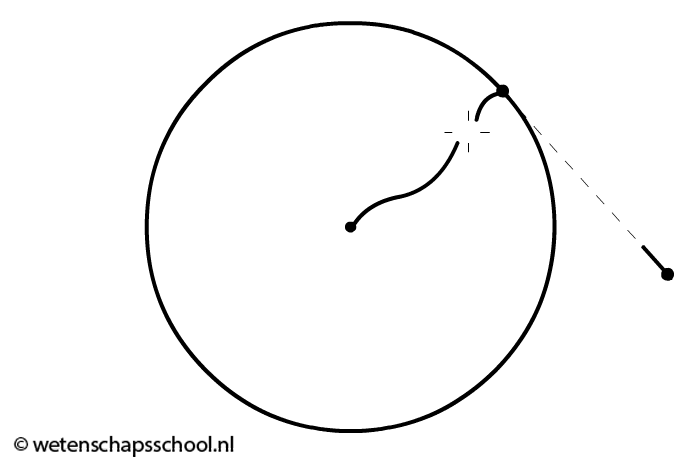
Als op een bepaald moment de middelpuntzoekende kracht zou wegvallen, dan zou het voorwerp (volgens de eerste wet van Newton) wegschieten in de richting die het op dat moment heeft. Het voorwerp schiet dan dus weg langs een raaklijn van de cirkelbaan (zie de onderstaande afbeelding).

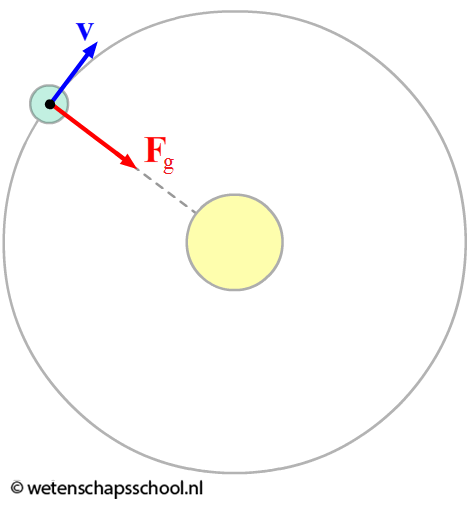
Een ander voorbeeld is het draaien van de aarde om de zon. Ook hier werkt een middelpuntzoekende kracht. In dit geval wordt deze kracht geleverd door de gravitatiekracht. Zonder deze kracht zou de aarde in een rechte lijn wegschieten van de zon.

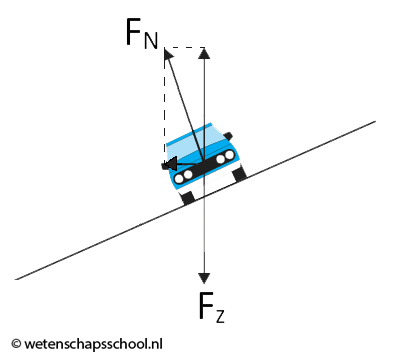
Er werkt ook een middelpuntzoekende kracht als een auto een bocht maakt. In dit geval wordt de middelpuntzoekende kracht geleverd door de wrijvingskracht tussen de wielen en de weg.

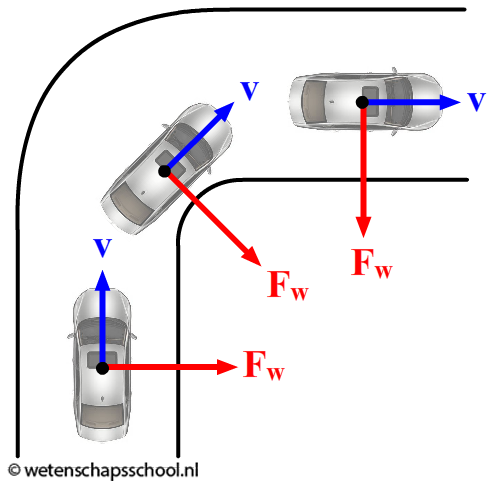
Deze extra wrijvingskracht wordt veroorzaakt doordat de bestuurder de voorwielen van de auto draait. De auto 'wil' rechtdoor, maar de wrijvingskracht forceert de auto in een cirkelbeweging. In de onderstaande afbeelding kan je zien dat auto's zo ontworpen zijn dat de wrijvingskracht op elk wiel naar hetzelfde middelpunt wijst.

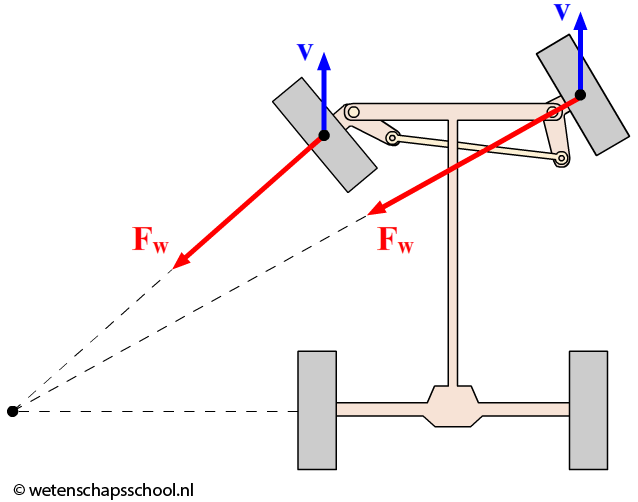
Als inzittende van een auto lijkt het alsof je bij het maken van een bocht naar de buitenbocht wordt geduwd. Dit is echter een illusie! Wat er gebeurt, is dat de inzittenden in een rechte lijn willen voortbewegen, terwijl de auto de bocht om gaat. Het is dus niet zo dat jij naar de buitenbocht wordt geduwd, maar juist dat de auto jouw de bocht in trekt!

Hetzelfde geldt voor het horizontaal rondslingeren van een steen aan een touw. Het lijkt alsof de steen een kracht naar buiten uitoefent, maar in werkelijkheid probeert de steen alleen maar rechtdoor te bewegen en is het jouw spierkracht die de steen in de cirkelbaan houdt.


klas 4
Als een vliegtuig een bocht wil maken, dan moet het vliegtuig zorgen voor een kracht loodrecht op de bewegingsrichting. Dit doet een vliegtuig door te kantelen (zie de onderstaande afbeelding). Op de vleugels werkt namelijk een liftkracht die altijd loodrecht op de vleugels werkt. Door te kantelen krijgt deze liftkracht een component in de horizontale richting. Deze horizontale component staat loodrecht op de bewegingsrichting van het vliegtuig en zal dus fungeren als een middelpuntzoekende kracht.

Om het gemakkelijker te maken voor auto's om de bocht door te komen wordt een soortgelijk effect gebruikt. Het wegdek wordt een beetje gekanteld, zodat de normaalkracht van de weg een horizontale component krijgt en kan fungeren als middelpuntzoekende kracht. Zonder deze normaalkracht zou alleen de wrijvingskracht de middelpuntzoekende kracht kunnen leveren en als deze kracht niet voldoende is, dan vliegt de auto uit de bocht.







Training
    Achterhaal in verschillende situaties welke kracht de middelpuntzoekende kracht levert en teken deze kracht in de juiste richting
  1. Geef in de volgende situaties aan welke kracht de middelpuntzoekende kracht levert:
    1. Een steen wordt horizontaal rondgeslingerd aan een touw.
    2. De aarde wordt in zijn baan gehouden om de zon.
    3. Een fietser gaat de bocht door.
    4. Kleding wordt rondgedraaid in een wasmachine.
    5. Een elektron wordt in zijn baan gehouden in een atoom.
  2. Leg uit wat er bedoeld wordt met dat de middelpuntzoekende kracht geen 'nieuwe soort kracht' is.
  3. Een auto maakt een bocht naar links en jij zit op een stoel rechts achterin de auto. Doordat de auto deze bocht maakt, hebt je het gevoel dat je uit de bocht geduwd wordt.
    1. Leg uit wat er werkelijk aan de hand is. Waarom voelt het dan toch zo?
    2. Schets welke kant je op zou vliegen als de auto een scherpe bocht maakt en er geen deuren zaten om je in de baan te houden.
  4. Een fietser rijdt door de regen. Het wiel draait snel genoeg dat druppels van het wiel af schieten. Teken op verschillende plaatsen op het wiel in welke richting de druppels wegschieten.
    5. Rekenen met de formule voor de middelpuntzoekende kracht
  5. Bereken de gravitatiekracht waarmee de maan in zijn baan om de aarde wordt gehouden. Bereken hiervoor eerst de snelheid van de maan met de formule uit de vorige paragraaf (2πr/T = v).
  6. Bereken de middelpuntzoekende kracht die werkt op een persoon met een massa van 80 kg op de evenaar ten gevolg van de draaiing van de aarde om zijn eigen as.
  7. Het internationaal ruimtestation heeft een massa van 4,2 × 105 kg en ondervindt een zwaartekracht van 3,9 × 106 N. Het ruimtestation bevindt zich in een baan 400 km boven het aardoppervlak. Bereken hoe lang het duurt voordat het ruimtestation een rondje om de aarde gemaakt heeft.
  8. Een proton wordt een magneetveld in geschoten en begint een cirkelbaan te maken. De magnetische kracht werkende op het proton is 8,36 × 10-24 N en de cirkelbaan heeft een straal van 2,00 cm. De omlooptijd van het proton is 12,7 ms. Bereken hiermee de massa van het proton.
  9. Een elektron beweegt binnen 1,52 × 10-16 s om de atoomkern in een waterstofatoom. De snelheid van het elektron is 2,1877 × 106 m/s. Bereken hiermee de elektrische kracht waarmee het elektron wordt aangetrokken tot de atoomkern.
  10. Hieronder zien we een indoorwielrenner. Zoals je kunt zien loopt de wielrenbaan in de bochten schuin.
    1. Leg uit waarom de helling schuin is gemaakt. Leg dit uit met behulp van de krachten die er werken.
    2. De voorste wielrenner heeft een massa van 70 kg. Bepaal aan de hand van de foto de middelpuntzoekende kracht die op deze wielrenner werkt. Maak hiervoor eerst een tekening van de krachten die er werken.

  11. (V) Een blokje aan een slinger maakt cirkelbewegingen zoals hieronder is aangegeven. De slinger heeft een lengte L van 20,6 cm en de hoogte h van 20 cm. De de hoek θ is 12°. De afbeelding is niet op schaal weergegeven.
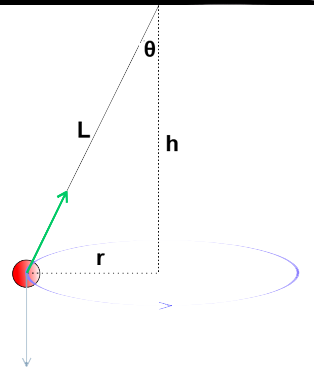
    1. De snelheid van het blokje hangt niet af van de massa. Laat dit zien. Leid hiervoor eerst af dat: $$ v = \sqrt{gr\tan\theta} $$
    2. Bereken de snelheid van het blokje.
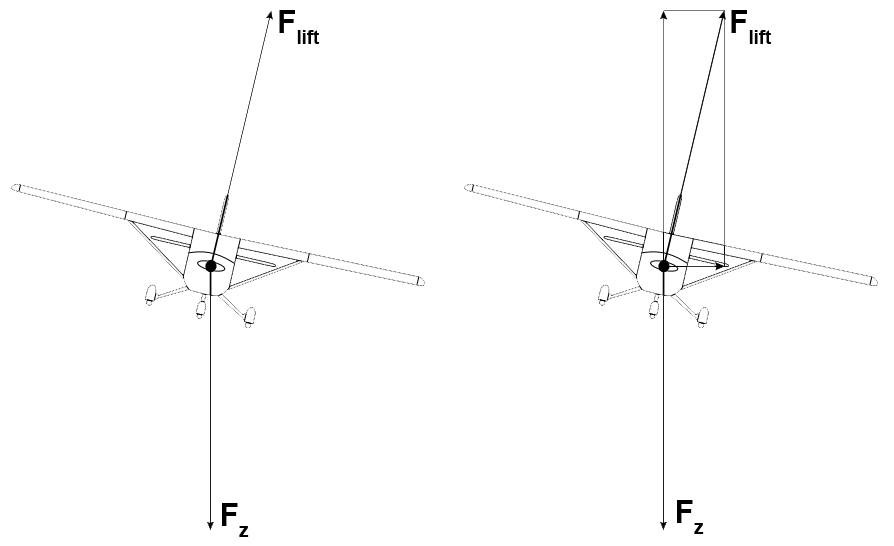
  12. Als een vliegtuig rechtdoor vliegt, dan is de zwaartekracht die op het vliegtuig werkt in evenwicht met de liftkracht die loodrecht op de vleugels werkt. Als het vliegtuig kantelt, dan zal het vliegtuig een bocht maken en ook een beetje dalen. Leg beide fenomenen uit aan de hand van de krachten die er werken.

    (bron: examen VWO 2017-1)
  13. (V) Een blokje aan een slinger maakt cirkelbewegingen zoals hieronder is aangegeven. De afbeelding is niet op schaal weergegeven.

    1. Laat zien dat de spankracht gegeven wordt door: $$ F_{span} = \frac{\tan\theta mgL}{r} $$ Maak hier zo nodig gebruik van \(\sin\alpha/\cos\alpha=\tan\alpha\)
    2. Laat ook zien dat de spankracht gegeven wordt door: $$ F_{span} = \frac{4\pi^2mL}{T^2}$$