Als afsluiter van dit hoofdstuk bestuderen we de valbeweging. In eerste instantie bestuderen we de vrije val. Dit is een val waarbij het voorwerp ongehinderd kan vallen. De luchtwrijvingskracht is in dit geval dus niet aanwezig of verwaarloosbaar klein (hetgeen betekent dat het effect ervan zo klein is dat het de beweging niet significant beïnvloedt).

Hieronder zien we een v,t-diagram van een vrije val. Zoals je ziet hebben we hier te maken met een eenparige versnelling. Een nauwkeurige aflezing van dit diagram geeft ons: $$ a = \frac{\Delta v}{\Delta t} $$ $$\frac{49,05}{5,00} = 9,81 m/s^2 $$



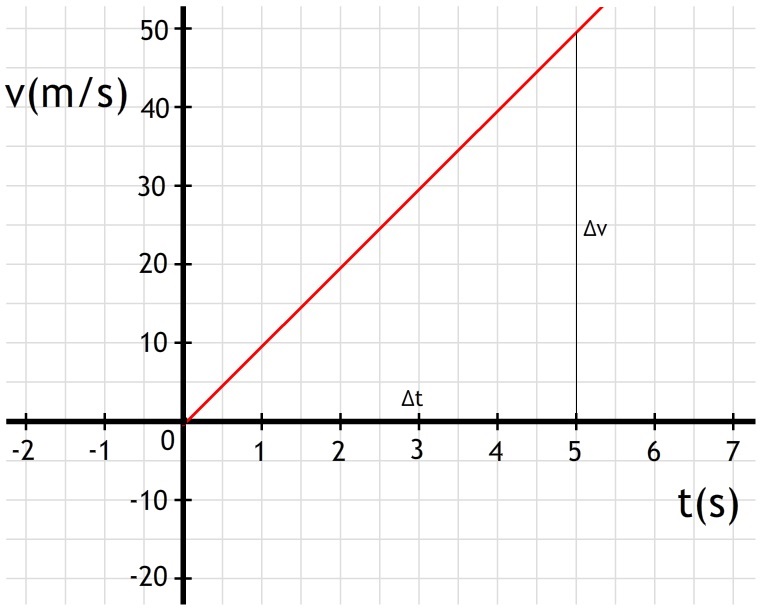
Deze versnelling is hetzelfde voor alle voorwerpen die vrij vallen. We noemen deze versnelling daarom ook wel de valversnelling (g). De waarde van deze versnelling wil je uit het hoofd kennen:

$$ g = 9,81 m/s^2 $$

Merk ook op in de bovenstaande grafiek dat de snelheid op tijdstip t=0 gelijk is aan nul. De versnelling is echter zelfs op dit moment al g=9,81 m/s2.


Klas 4

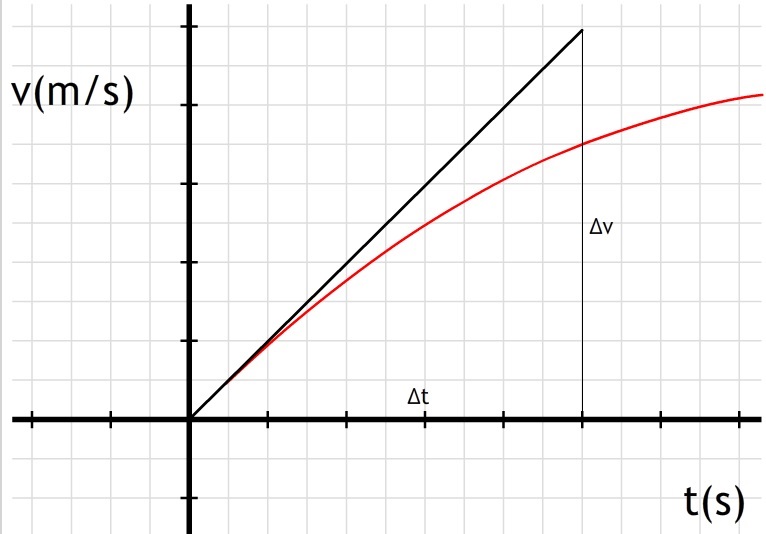
In het volgende v,t-diagram zien we een val waarbij de luchtwrijvingskracht wel een significante rol speelt. Zoals je kunt zien wordt de versnelling langzaam kleiner. Alleen op tijdstip t=0s is de versnelling nog gelijk aan de valversnelling (g). Dit komt omdat de snelheid op dit moment nul is en daardoor de luchtwrijvingskracht ook gelijk is aan nul. Als we op dit tijdstip dus een raaklijn tekenen, dan vinden we dus alsnog de valversnelling g terug (zie het onderstaande diagram).





Training
    Een val beschrijven in een (x,t)- en (v,t)-diagram met en zonder wrijvingskracht.
  1. Teken een (x,t)- en een (v,t)-diagram van een vallende steen zonder luchtwrijvingskracht.
  2. Klas 4 Teken een (x,t)- en een (v,t)-diagram van een vallende steen met luchtwrijvingskracht.
    3. De valversnelling bepalen in een (v,t)-diagram met en zonder wrijvingskracht.
  3. Klas 4 In het onderstaande (x,t)- en (v,t)-diagram wordt een valbeweging beschreven.
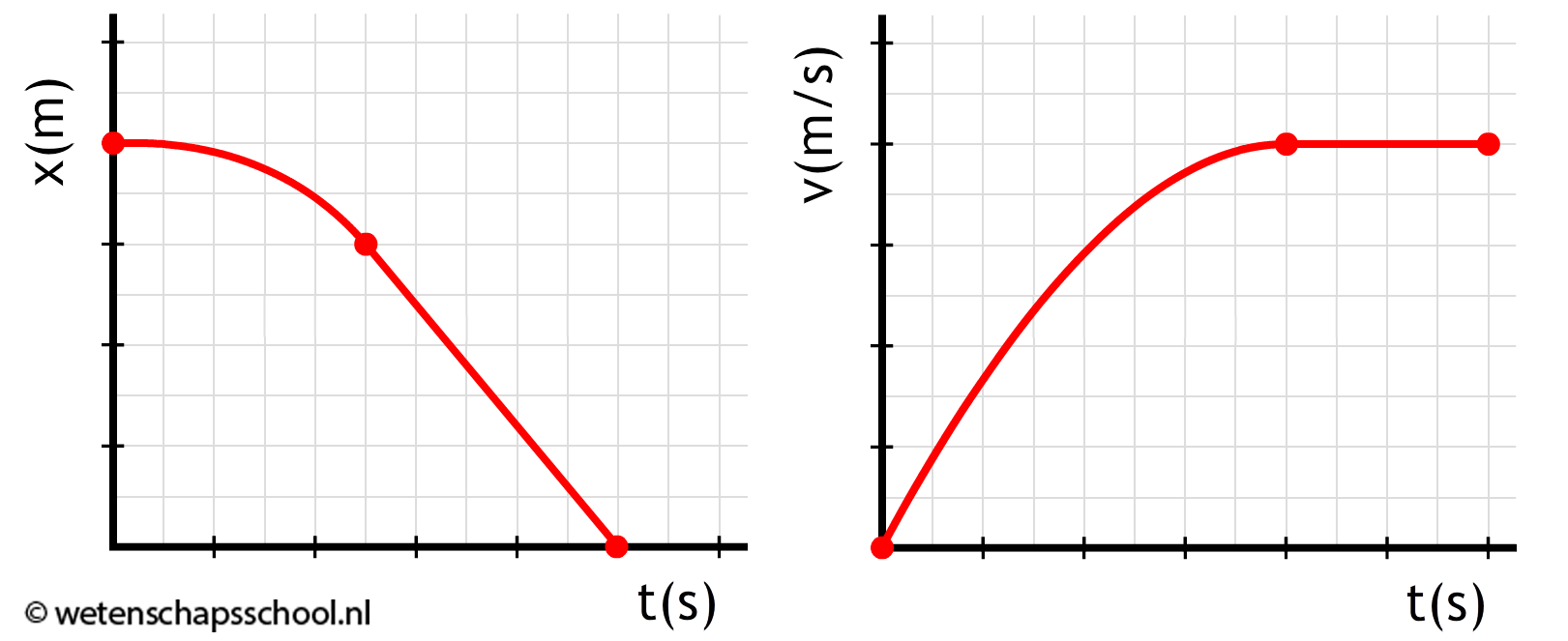
    1. Leg uit hoe je aan beide diagrammen kan zien dat de wrijvingskracht niet te verwaarlozen is.
    2. Wat is de snelheid van het voorwerp op t = 0?
    3. Wat is de versnelling van het voorwerp op t = 0?
  4. De maan heeft geen atmosfeer en dus ook geen wrijvingskracht. Teken een (v,t)-diagram van de beweging van de maan.
  5. Vul het online logboek aan. Schrijf hier in ieder geval iets over wat een vrije val is. Schrijf ook iets over de snelheid en de versnelling op het moment dat een voorwerp vanuit stilstand losgelaten wordt.
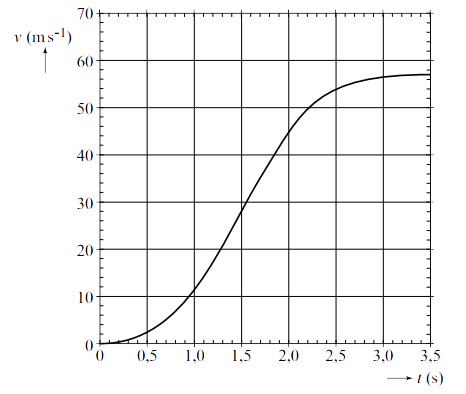
  6. Klas 4 In de onderstaande grafiek wordt het (v,t)-diagram van een parachutesprong weergegeven.
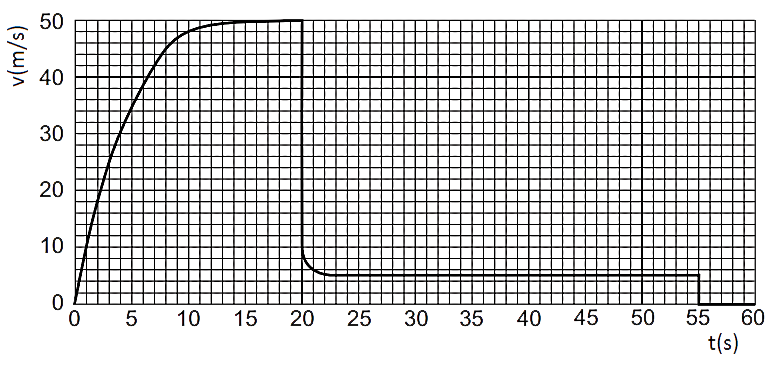
    1. Bereken met behulp van de grafiek de valversnelling g.
    2. Wat was de topsnelheid van de springer?
    3. Van hoe hoog is de springer gesprongen?
  7. In het onderstaande (v,t)-diagram zien we de versnelling van een karretje op een horizontale baan aan het begin van een supersnelle achtbaan.
    1. Een leerling analyseert de grafiek en concludeert dat we hier eerst te maken hebben met een versnelling en dat het voorwerp daarna vertraagt totdat de snelheid constant is. Heeft de leerling gelijk?
    2. Klas 4 Vind de maximale versnelling die de achtbaankar ondergaat en druk je antwoord uit in g
    3. Bereken de lengte van de horizontale baan.
    4. Klas 4 Bereken de gemiddelde snelheid van de achtbaankar op dit traject op twee manieren.
    5. Klas 4 Bereken de gemiddelde versnelling van de achtbaankar.
  8. Het onderstaande (v,t)-diagram beschrijft een sprong van een volleybalspeler.
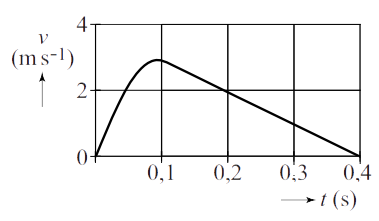
    1. Op welk moment bereikt de speler het hoogste punt van zijn sprong? Leg je keuze uit.
    2. Bepaal met behulp van het diagram hoe hoog de persoon gesprongen heeft.
    3. Klas 4 Bepaal de versnelling die de springer bij het begin van het afzetten ondervond.
    4. Klas 4 Ga na of de wrijvingskracht van de springer verwaarloosbaar is.
    5. Klas 4 Schets hoe de grafiek eruit zou zien als de springer twee identieke sprongen achter elkaar zou maken.
  9. In de onderstaande afbeelding zien we een zogenaamde bungeetrampoline. Een persoon kan hier met behulp van twee elastische koorden en een trampoline erg hoog springen.

    Hieronder zien we het (v,t)-diagram van een persoon in het apparaat.
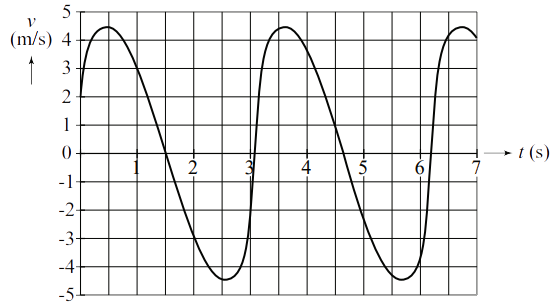
    1. Geef een tijdstip waarbij de springer zich op zijn hoogste en zijn laagste punt bevindt. Leg uit hoe je op je antwoord komt.
    2. Klas 4 Bereken de maximale snelheid en de maximale versnelling die de persoon ondergaat bij het afzetten tegen de trampoline.
    3. Klas 4 Ga na of de persoon op het hoogste punt nog steeds een kracht van de elastische koorden ondervindt of dat deze op dat moment niet gespannen zijn. Je mag ervan uitgaan dat de wrijvingskrachten verwaarloosbaar zijn.
  10. Klas 4 Een leerling bestudeert een speelgoedsprinkhaan. Onder het lijf van de sprinkhaan zit een zuignap, die zich op de ondergrond vastzuigt als je de sprinkhaan stevig naar beneden drukt. Wanneer er lucht onder de zuignap komt, springt de sprinkhaan omhoog doordat zijn poten als veren werken.
    Hieronder zien we een (h,t)-diagram van de beweging van de sprinkhaan.

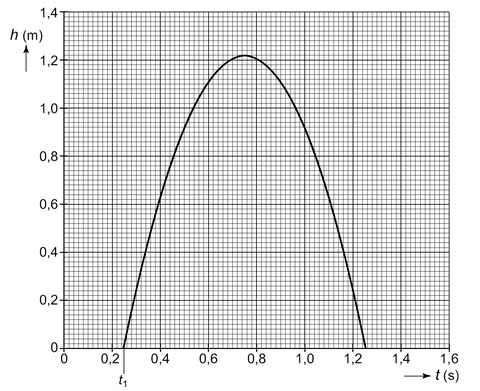    Bepaal met behulp van dit figuur of de sprinkhaan een meetbare luchtwrijvingskracht heeft ondervonden.
  11. Vul het online logboek aan.