In deze paragraaf gaan we meer leren over de versnelling. Hieronder zien we bijvoorbeeld twee auto's die optrekken.

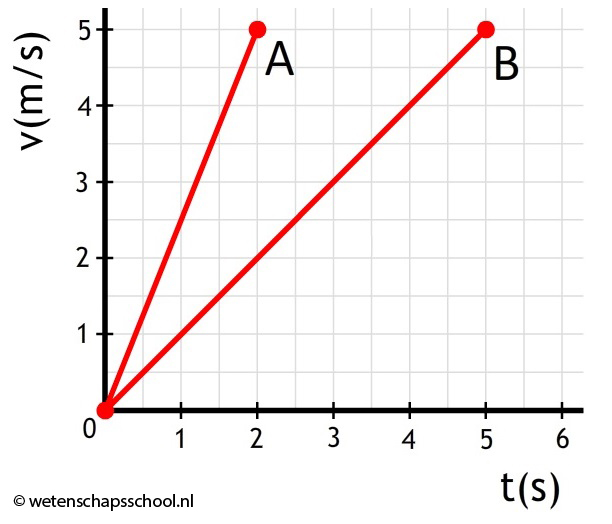
Auto A trekt sneller op en heeft dus een grotere versnelling. In een (v,t)-diagram geldt dus:

Steiler = grotere versnelling

Hoe groot de versnelling in beide gevallen is kunnen we als volgt uitrekenen:

$$ \frac{\Delta v}{\Delta t} = a$$
Toename van snelheid (Δv) meter per seconde (m/s)
Tijdsduur (Δt) seconde (s)
Versnelling (a) meter per seconde per seconde (m/s2)

De toename van de snelheid wordt beschreven door:

$$ \Delta v = v_{eind} - v_{begin} $$
Beginsnelheid (vb) meter per seconde (m/s)
Eindsnelheid (ve) meter per seconde (m/s)
Toename van snelheid (Δv) meter per seconde (m/s)

Laten we dit eens toepassen. Neem bijvoorbeeld de onderstaande grafiek. De snelheid loopt van 1 tot 4 m/s. De toename van de snelheid (Δv) is dus 4 - 1 = 3 m/s. De tijdsduur (Δt) is 6 seconden. De versnelling is dus gelijk aan:

$$\frac{\Delta v}{\Delta t} = a$$ $$ \frac{3,0}{6,0} = 0,50 \text{ m/s}^2 $$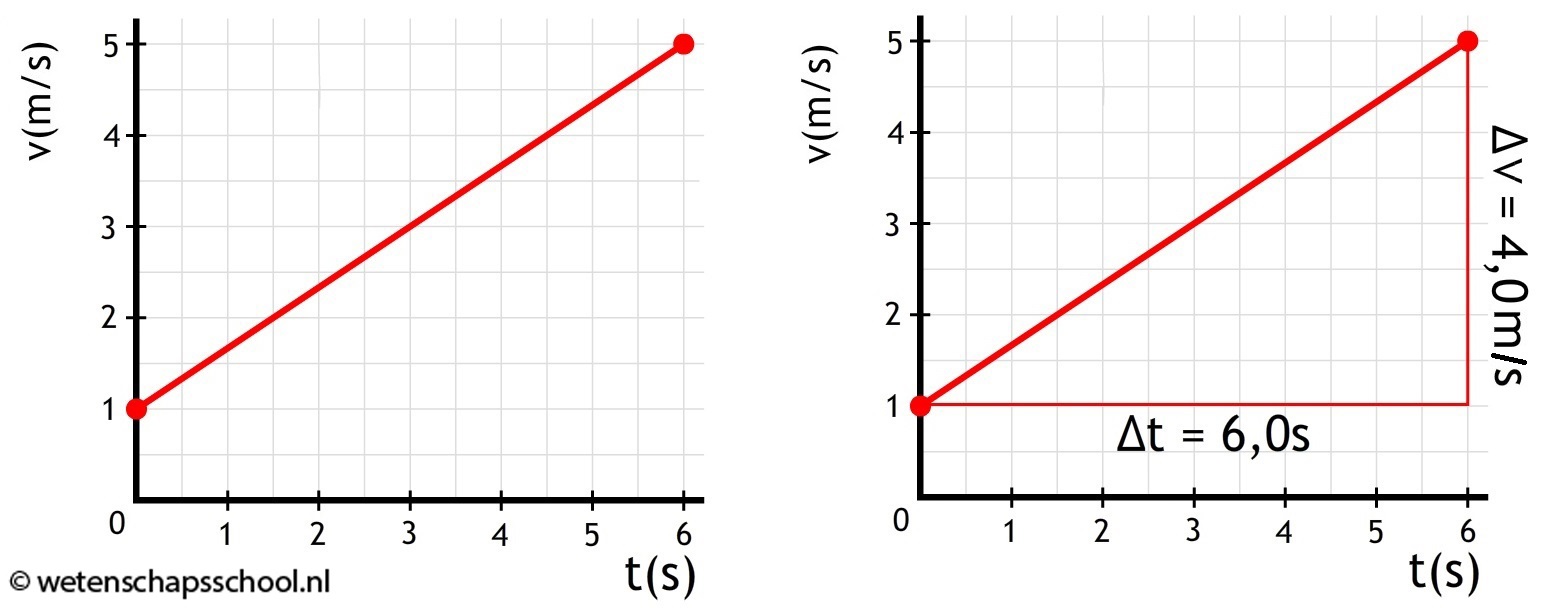

We zien hier dat de eenheid van de versnelling gelijk is aan m/s2. Waar komt dit vandaan? In het bovenstaande voorbeeld zien we bijvoorbeeld dat de snelheid elke seconden 0,5 m/s toeneemt. We hebben dus een toenamen van 0,5 meter per seconde per seconde toeneemt (0,5 m/s/s). Dit kunnen we wiskundig korter opschrijven als 0,5 m/s2.

We hebben het in dit hoofdstuk gehad over de toename van de snelheid (Δv) en de gemiddelde snelheid (vgem). Bij het beantwoorden van vragen is het belangrijk deze begrippen goed uit elkaar te houden. In het bovenstaande voorbeeld is de toename van de snelheid gelijk aan 4 - 1 = 3 m/s, terwijl de gemiddelde snelheid gelijk is aan (1 + 4)/2 = 2,5 m/s.

Ook vertraging kunnen we met deze formule beschrijven. Stel dat een auto gedurende 4 seconden vertraagt van 40 m/s naar 12 m/s. Er geldt nu:

$$\Delta v = 12 - 40 = -28 \text{ m/s}$$

De versnelling wordt:

$$a = \frac{\Delta v}{\Delta t} $$ $$ \frac{-28}{4} = -7 \text{ m/s}^2$$

Een versnelling van -7 m/s2 vertelt ons dat de snelheid elke seconde 7 m/s afneemt. Een negatieve versnelling is dus gelijk aan een vertraging. Let er op dat dit niet hoeft te betekenen dat het voorwerp achteruit beweegt! Een remmende auto vertraagt bijvoorbeeld, maar gaat wel vooruit.


Klas 4

In het volgende diagram bepalen we met behulp van een (v,t)-diagram de versnelling op een punt A. Net als in de eerste paragraaf gebruiken we hiervoor een raaklijn:



Ook de gemiddelde versnelling kunnen we met het (v,t)-diagram bepalen. We gebruiken dan: $$ \frac{\Delta v}{\Delta t} = a_{gem} $$ In het bovenstaande diagram vinden we dan: $$ \frac{3,4}{6,0} = 0,57 \text{ m/s}^2 $$



Training
    De eenheid van versnelling.
  1. Leg duidelijk uit waarom de eenheid van de versnelling m/s/s (oftewel m/s2) is.
  2. Klas 4 Laat met behulp van de formule uit deze paragraaf zien dat de eenheid van de versnelling daadwerkelijk m/s2 is.
  3. Klas 4 De relatie tussen de valtijd (t) van een voorwerp en de valhoogte (h) wordt gegeven door: $$ h = \frac{1}{2}gt^2 $$
    1. Laat zien dat g in deze vraag de eenheid heeft die hoort bij de versnelling.
    2. Het resultaat van een aantal metingen staat in de onderstaande tabel:
      Hoogte (m)    Tijd (s)
      0   0
      10   1,4
      20   2,0
      30   2,5
      40   2,9
      Linearizeer de grafiek en bepaal hiermee de waarde van g.
  4. Vul het online logboek aan.
    5. De versnelling bepalen in een (v,t)-diagram.
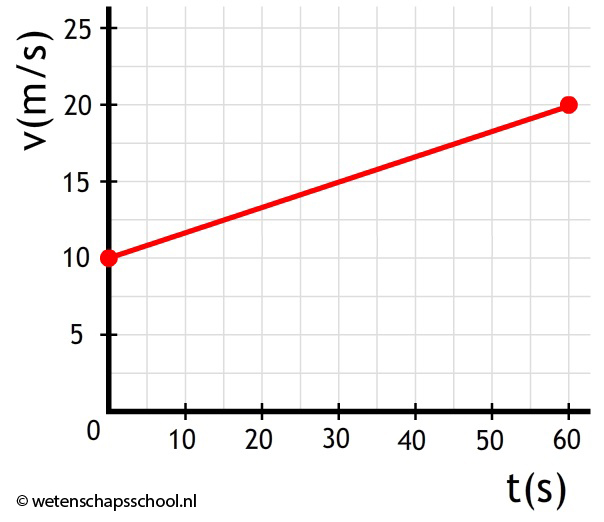
  5. Bereken de versnelling van de volgende beweging:
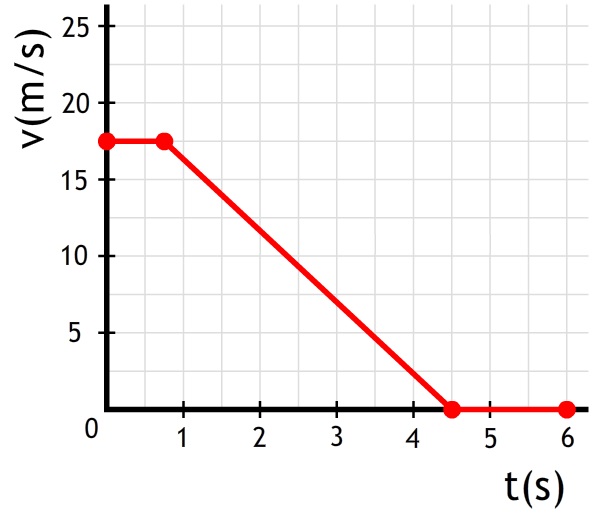
  6. Bereken de vertraging die het voertuig ondergaat tijdens het remmen:
  7. Het volgende diagram bestaat uit drie delen. Bereken voor elk deel de versnelling.
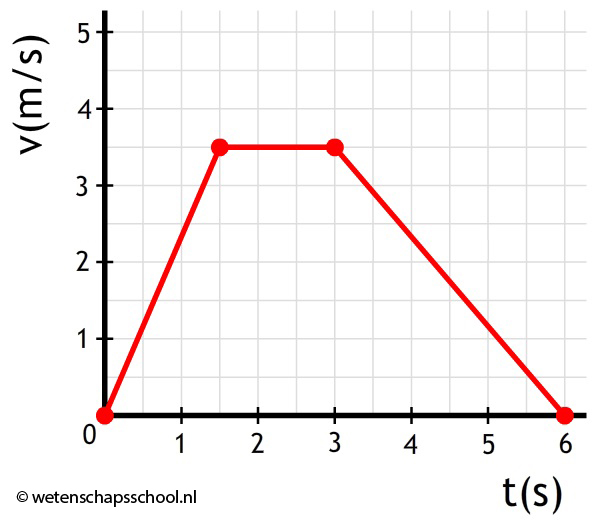
  8. Klas 4 Bereken de versnelling op tijdstip t = 20s:
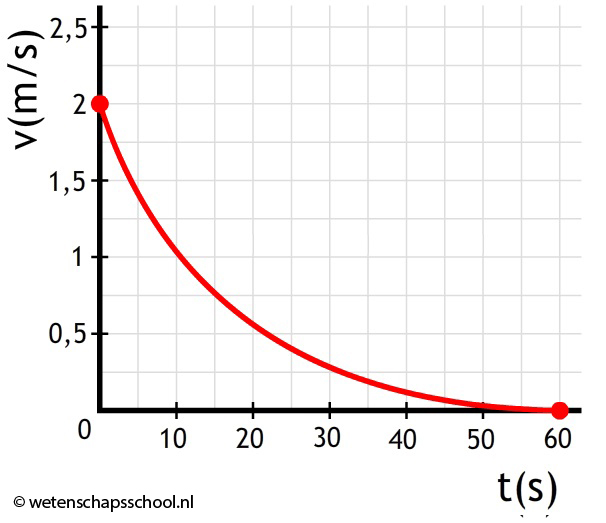
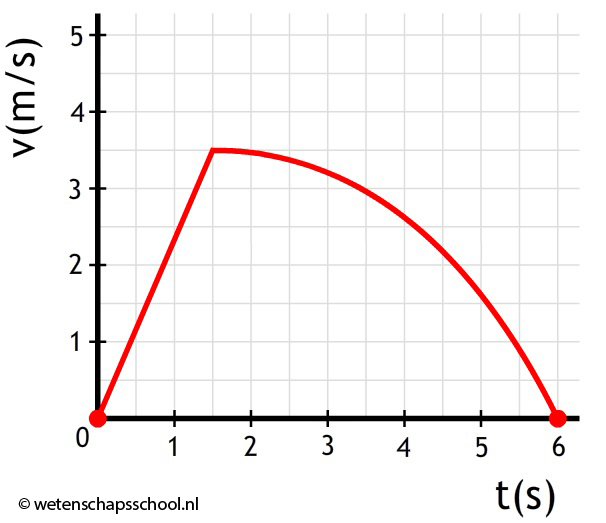
  9. Klas 4 Hieronder is de beweging van een optrekkende auto beschreven. Bereken de maximale versnelling en de maximale snelheid tijdens de beweging.
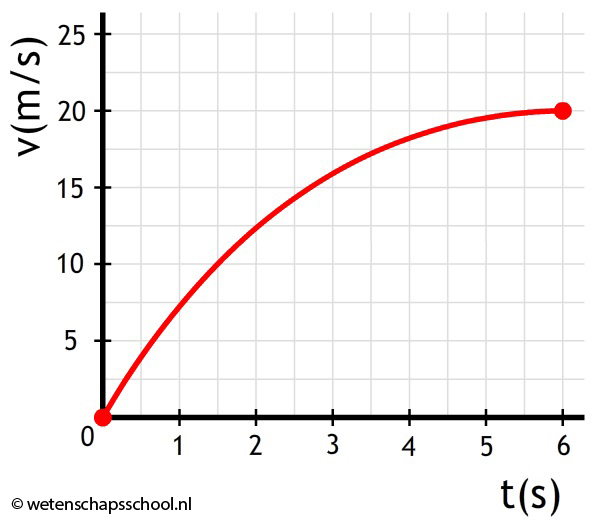
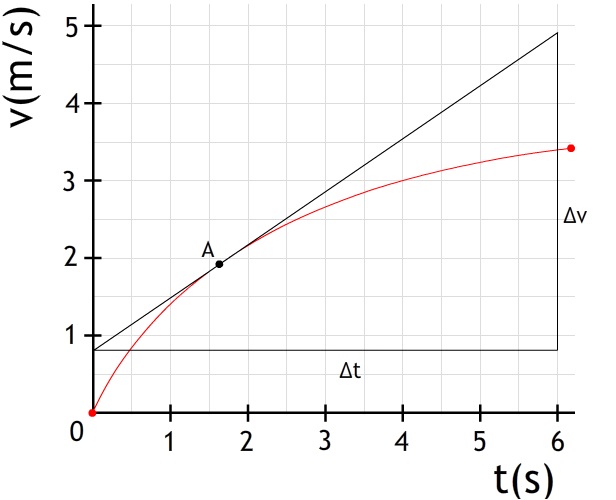
  10. Klas 4 Bereken de versnelling op tijdstip t = 1s en t = 4s.

  11. Vul het online logboek aan.
  12. Hieronder is een (v,t)-diagram weergegeven waarbij de beweging van een jojo weergegeven is. Op tijdstip t=0 is het koord volledig om de jojo gewikkeld en laat de persoon de jojo los.
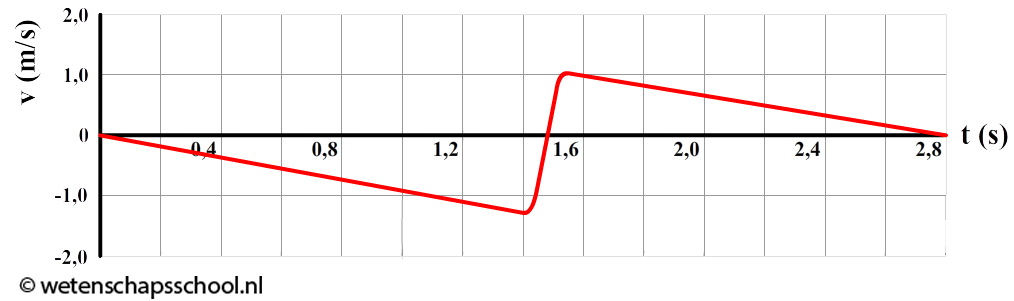
    1. Leg uit op welk moment de jojo op zijn laagste punt is.
    2. Bereken de lengte van het koord.
    3. Op het laagste punt ondergaat de jojo een plotselinge versnelling waarbij de jojo van richting verandert. Geef de versnelling waarmee dit gebeurt.
  13. Klas 4 Hieronder is het (a,t)-diagram van de beweging van een persoon in een lift weergegeven.
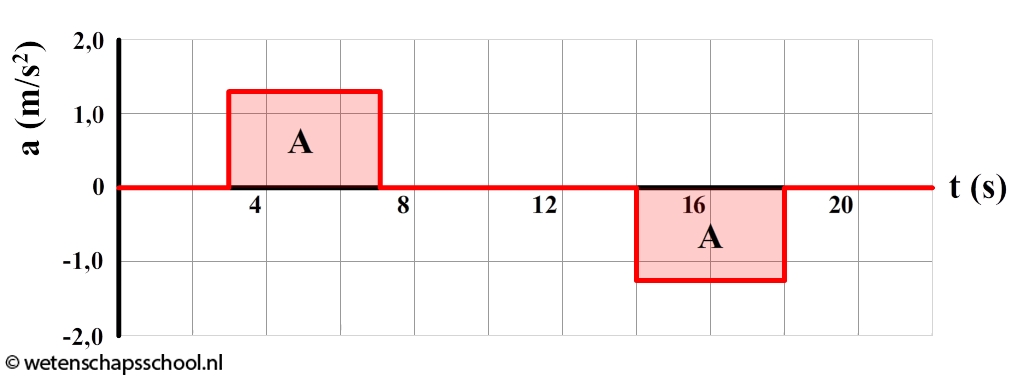
    1. Geef aan op welke moment de lift stilstaat, constant beweegt, versnelt of vertraagt.
    2. De twee oppervlaktes de A zijn genoemd in de afbeelding zijn even groot. Leg uit waarom dit noodzakelijk het geval moet zijn.
    3. Bereken de maximale snelheid van de lift
  14. Vul het online logboek aan.