Eerder in dit hoofdstuk hebben we geleerd dat we de snelheid uit kunnen rekenen met deze formule:

$$\frac{\Delta x}{\Delta t} = v$$

Deze formule blijkt ook bruikbaar als de snelheid tijdens een beweging niet constant geweest is. Wat we dan vinden is echter niet 'de snelheid', maar de gemiddelde snelheid van de beweging. We schrijven dan:

$$\frac{\Delta x}{\Delta t} = v_{gem}$$

Verplaatsing (Δx)	meter (m)
Tijdsduur (Δt)	seconde (s)
Gemiddelde snelheid (v_gem)	meter per seconde (m/s)

Het simpelste voorbeeld van een niet-constante snelheid is een geleidelijke versnelling. We noemen dit ook wel een eenparige versnelling. In dit geval kunnen we de gemiddelde snelheid ook als volgt uitrekenen:

$$ \frac{v_{b}+v_{e}}{2} = v_{gem} $$

Beginsnelheid (v_b)	meter per seconde (m/s)
Eindsnelheid (v_e)	meter per seconde (m/s)
Gemiddelde snelheid (v_gem)	meter per seconde (m/s)

Stel dat een auto bijvoorbeeld versnelt van 10 m/s naar 30 m/s, dan is de gemiddelde snelheid gelijk aan:

$$ \frac{10+30}{2} = 20 \text{ m/s} $$

Let erop dat je bij deze berekening in je rekenmachine haakjes gebruikt:

$$ (10 + 30 )/2 = 20 \;\;\;\;\;\;\; \text{ rekenmachine} $$

Tijd om een opdracht te bespreken waarbij we van beide formules gebruik maken:

Voorbeeld

Opdracht: Een auto versnelt gedurende 10 seconden van 20 naar 30 m/s. De versnelling was eenparig. Hoeveel meter heeft de auto dan afgelegd?

Antwoord: Eerst berekenen we de gemiddelde snelheid:

$$v_{gem} = \frac{v_{\text{begin}}+v_{\text{eind}}}{2} = \frac{20 + 30}{2} = 25 \text{ m/s}$$

Met de gemiddelde snelheid kunnen we de afstand uitrekenen:

$$\Delta x = v_{gem} \times \Delta t = 25 \times 10 = 250 \text{ m}$$

De auto heeft tijdens de versnelling dus 250m afgelegd.

In het onderstaande voorbeeld bespreken we nog een manier om de gemiddelde snelheid te vinden:

Voorbeeld

Opdracht: Bereken de gemiddelde snelheid van de volgende beweging:

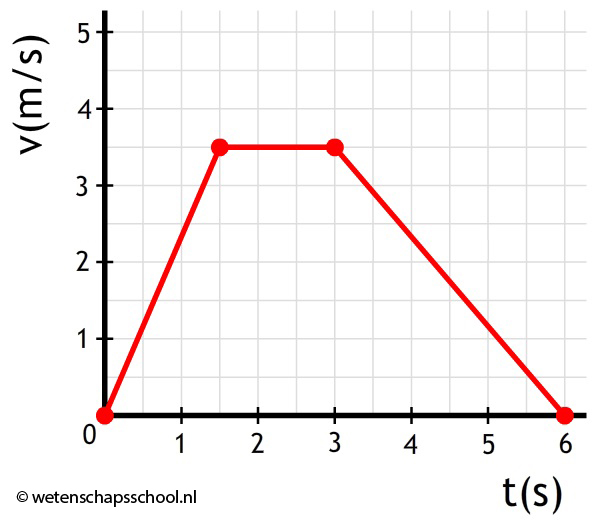
Antwoord: Het oppervlak onder de grafiek is gelijk aan de verplaatsing Δx. Het oppervlak is:

$$ \frac{1,5 \times 3,5}{2} + 1,5 \times 3,5 + \frac{3 \times 3,5}{2} = 13,1 \text{ m} $$

In de grafiek zien we ook dat de beweging 6 seconden geduurd heeft. Met deze gegevens kunnen we de gemiddelde snelheid berekenen:

$$v_{gem} = \frac{\Delta x}{\Delta t} = \frac{13,1}{6} = 2,2 \text{ m/s}$$

Het voorwerp heeft dus een gemiddelde snelheid van 2,2 m/s gehad.

Klas 4

Als de versnelling niet eenparig is, dan kunnen we de gemiddelde snelheid bepalen met het (v,t)-diagram. Stel dat we bijvoorbeeld de gemiddelde snelheid willen weten van de onderstaande beweging van tijdstip t = 1,0 s tot t = 5,0 s. Dit doen we door een horizontale lijn te trekken, waarbij de missende oppervlaktes onder de lijn (A genoemd) even groot zijn als de oppervlakte onder de grafiek boven de lijn (B genoemd). De hoogte van de lijn is de gemiddelde snelheid (in dit geval 3,7 m/s).

In het volgende filmpje worden alle manieren om de gemiddelde snelheid te berekenen nog eens besproken:

Training

Rekenen met Δx/Δt=v_gem en (v_b+v_e)/2=v_{gem.

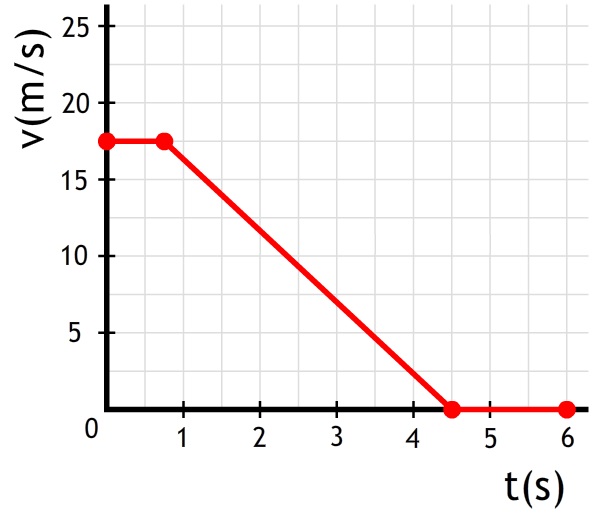
Een auto versnelt eenparig in 12 seconden van 10 m/s naar 35 m/s. Hoeveel afstand heeft de auto tijdens deze beweging afgelegd? Je mag aannemen dat de versnelling eenparig is.
Een auto trekt met een eenparige versnelling vanuit stilstand op tot 40 m/s en legt een afstand van 950 meter af. Hoe lang heeft de auto over deze versnelling gedaan?
Een automobilist die met een snelheid van 80 km/h rijdt, trapt op zijn rem totdat hij stil staat. Het remmen duurt 4 seconden. Wat is de remweg van de bestuurder?
Een parachutespringer daalt met een snelheid van 200 km/h als hij zijn parachute opentrekt. Na 0,70 s is zijn snelheid gedaald tot 40 km/h. Bereken hoeveel meter de parachutist in de tussentijd heeft afgelegd.
Een bestuurder van een brommer probeert een tractor in te halen. Hij versnelt hiervoor gedurende 4 seconden en legt in deze tijd 100 meter af. Zijn beginsnelheid was 10 m/s. Welke snelheid heeft de brommer na de versnelling?
Een automobilist versnelt eenparig over een afstand van 1500 meter en behaald een eindsnelheid van 40 m/s. De versnelling heeft 50 seconden geduurd. Wat was de beginsnelheid van de auto?
Vul het online logboek aan.

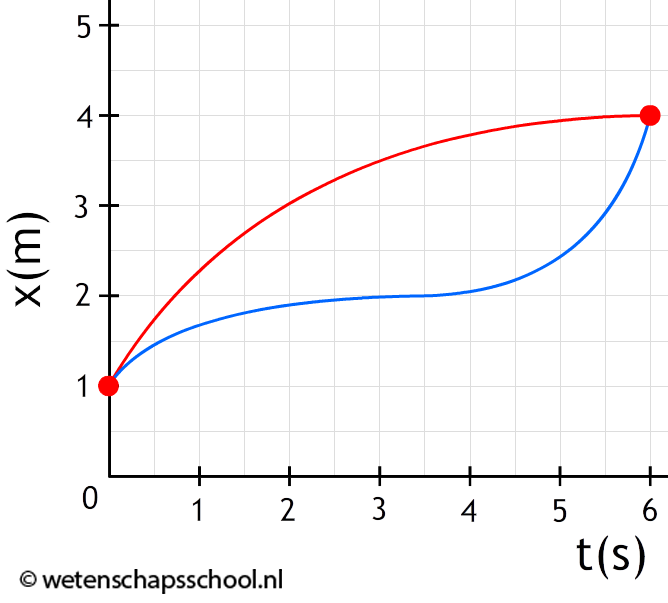
Bepalen van de gemiddelde snelheid met behulp van een (v,t)-diagram.

Hieronder zien we twee bewegingen weergegeven in een (x,t)-diagram. Bepaal in beide gevallen de gemiddelde snelheid. Vergelijk daarna de antwoorden. Verklaar wat je ziet.

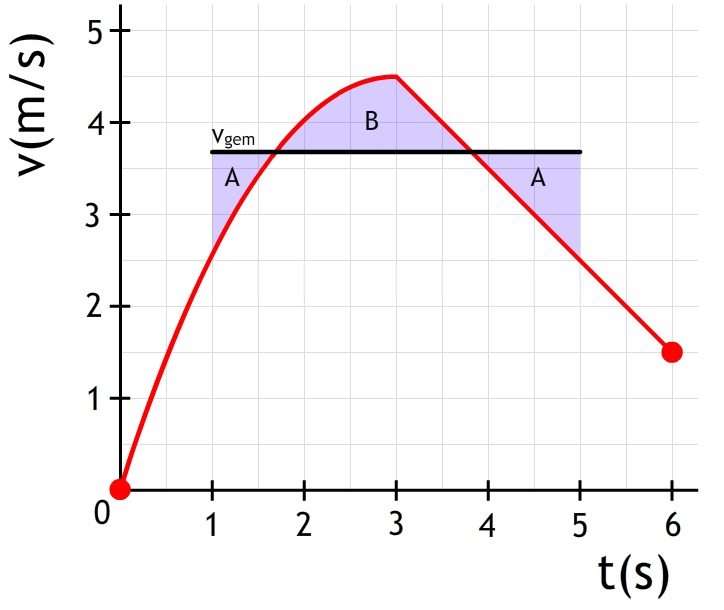
Bereken de gemiddelde snelheid van de volgende beweging. Bereken hiervoor eerst
de totale afstand die het voorwerp heeft afgelegd.

Een leerling loopt eerst 3 seconden met een constante snelheid van 1,2 m/s.
Dan staat de leerling 2 seconden stil. Uiteindelijk loopt de leerling
nog 4 seconden met een constante snelheid van 1,5 m/s.

Teken het v,t-diagram bij deze beweging.
Bereken de afgelegde afstand.
Teken het bijbehorende (x,t)-diagram
Wat is de gemiddelde snelheid van de leerling?

In het volgende diagram is het remmen van een auto beschreven. Bereken de gemiddelde snelheid van het voertuig tijdens de stopafstand.

Vul het online logboek aan.

Klas 4
In de onderstaande afbeelding zien we het (v,t)-diagram van een zwemslag. Zoals je ziet zitten er twee pieken in de snelheid. De eerste komt van de beweging van de armen en de tweede van de beweging van de benen.

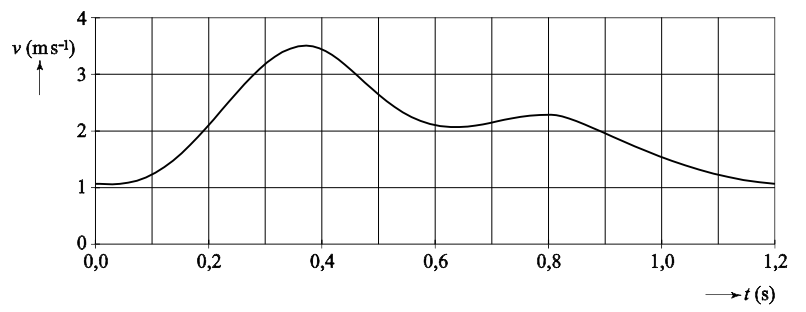
Bereken de gemiddelde snelheid van de zwemmer tijdens de eerste 0,5 seconden.
Bereken hoeveel afstand de zwemmer in deze tijd heeft afgelegd.

Klas 4
Vul het online logboek aan.}