In deze paragraaf gaan we met de dichtheid uitrekenen of voorwerpen drijven of zinken. We zullen dit o.a. gebruiken om te begrijpen waarom zware boten toch blijven drijven.

Met de dichtheid kunnen we o.a. voorspellen of een voorwerp zal drijven of zinken. Als een voorwerp een grotere dichtheid heeft dan de omringende vloeistof, dan zal het voorwerp zinken. Als het een lagere dichtheid heeft, dan blijft het drijven.

Piepschuim heeft bijvoorbeeld een lagere dichtheid dan water en blijft dus drijven (zie de onderstaande afbeelding). Dit geldt zelfs als je een gigantisch stuk piepschuim van duizenden kilogram in het water zou leggen. Het omgekeerde is waar voor een stukje metaal. Dit heeft een grotere dichtheid en als gevolg zal zelfs het lichtste stukje metaal zinken.






Klas 3

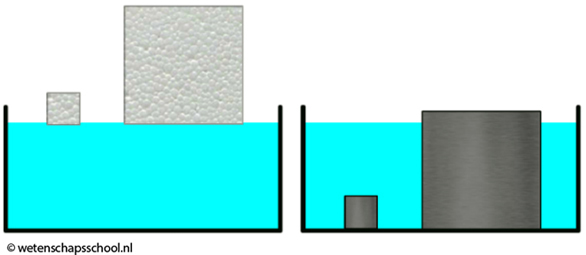
Hieronder zien we een gigantisch containerschip met een grote massa. Hoe kan het dat dit schip blijft drijven?

We gaan dit begrijpen met behulp van een simpel voorbeeld. Stel we hebben een stalen plaat van 7800 kg met een lengte van 5,0 meter, een breedte van 10,0 meter en een dikte van 2,0 centimeter. Het volume van de plaat is in dat geval 5,0 × 10,0 × 0,020 = 1,0 m3. De dichtheid wordt dan:

$$ \rho = \frac{m}{V} $$ $$ \frac{7800}{1,0} = 7800 \text{ kg/m}^3 (= 7,8 \times 10^3 \text{ kg/m}^3) $$

Deze dichtheid is veel groter dan de dichtheid van water (998 kg/m3) en als gevolg daarvan zal de plaat dus zinken.

Nu bouwen we een dun muurtje aan de randen van de stalen plaat. We maken het muurtje 16,0 cm hoog en zorgen dat het muurtje zo dun is dat het zo goed als niets weegt (zie de onderstaande afbeelding).

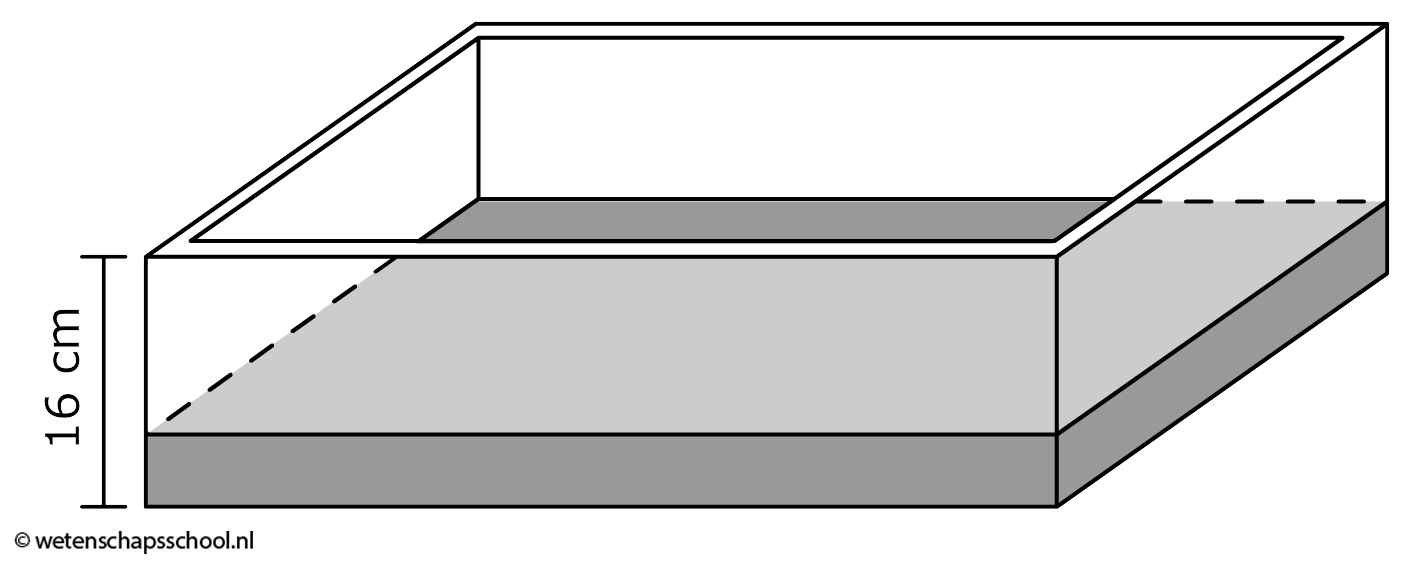
Het totale volume van onze boot is nu 5,0 × 10,0 × 0,160 = 8,0 m3. De dichtheid wordt in dit geval:

$$ \rho = \frac{m}{V} $$ $$ \frac{7800}{8,0} = 975 \text{ kg/m}^3 (= 9,8 \times 10^2 \text{ kg/m}^3) $$

Dit is kleiner dan de dichtheid van water (998 kg/m3) en als gevolg daarvan zal de boot dus drijven! Een klein muurtje van 16 cm is dus al genoeg om een stalen plaat van 7800 kg te laten drijven! Met behulp van dit principe worden ook containerschepen ontworpen.





Training
    Berekenen of voorwerpen drijven of zinken
  1. (2,3) In de onderstaande afbeelding zien we dat een moer van ijzer gewoon blijft drijven op het metaal kwik. Wat zegt dit over de dichtheden van ijzer en kwik? Ga na of je antwoord klopt met behulp van de tabel in de paragraaf.

  2. (2,3) Je gooit een ijsblokje eerst in een glas water en dan in een glas alcohol. Ga voor beide gevallen na of het ijsblokje blijft drijven. Leg uit hoe je op je antwoord komt.
  3. (2,3) De zoutconcentratie van de dode zee is erg groot. Dit zorgt ervoor dat mensen hier erg goed op drijven. Wat zegt dit over het verschil tussen de dichtheid van zoet en zout water?
  4. (2,3) Een voorwerp heeft een volume van 350 mL en een massa van 340 gram.
    1. Drijft dit voorwerp in water of niet?
    2. Zonnebloemolie heeft een dichtheid van 0,92 g/cm3. Drijft dit voorwerp in zonnebloemolie of niet?
  5. (2,3)
    1. Een plank heeft een massa van 10 kg. De plank is 2 cm dik, 10 cm breed en 80 cm lang. Bereken of de plank blijft drijven.
    2. We zagen een kwart van de plank af. Bereken of de plank nu blijft drijven.
    3. Verklaar het antwoord van vraag b.
  6. (2,3) In een experiment in de klas wordt de dichtheid van een leerling bepaald. Eerst wordt met een weegschaal de massa van de leerling bepaald. De leerling blijkt 45 kg te wegen. Dan wordt er een bak met water de klas in gereden. De bak heeft een lengte van 1,0 m en een breedte van 60 cm. Het water komt 40 cm hoog. De leerling stapt nu in de bak water en gaat helemaal kopje onder. Als de leerling heeft uitgeademd wordt de nieuwe hoogte van het water gemeten. Dit blijkt 47,3 cm te zijn.
    1. Bereken de dichtheid van de leerling.
    2. Ga ook na of de leerling drijft of zinkt.
    3. Leg uit of je het antwoord bij vraag b verwacht had.
  7. (3) Een scubadiver gebruikt een buoyancy control device (BCD) om in het water te zinken of drijven. Om te zinken laat de duiker lucht uit de BCD stromen.
    1. Leg uit dat dit ervoor kan zorgen dat de duiker zinkt.
    2. Om weer boven water te komen laat de duiker wat lucht van de zuurstoffles in de BCD stromen. Leg uit waarom dit werkt.
    3. De BCD kan ook gebruikt worden om net te blijven zweven op dezelfde plek onder water. Leg uit hoe dit werkt.
    8. Bereken of een boot drijft of zinkt
  8. (3) Een boot wordt in het water gelegd. De boot heeft een massa van 15000 kg. De boot heeft de vorm van een balk. De lengte is 5,0 m, de breedte 3,0 m en de hoogte 90 cm. Bereken of deze boot zinkt of drijft.
  9. (3) Een ijzeren plaat heeft een lengte van 5,0 m, een breedte van 2,5 m en een dikte van 5 centimeter. Om de plaat wordt een muurtje gemaakt met een verwaarloosbare massa.
    1. Bereken de massa van de ijzeren plaat.
    2. Hoe hoog moet het muurtje zijn wil de boot net blijven drijven?
  10. (3V) Een ijzeren plaat heeft een lengte van 5,0 m, een breedte van 2,5 m en een dikte van 5 centimeter. Om de plaat wordt een muurtje gebouwd van 1,0 meter. De massa van het muurtje zelf is verwaarloosbaar. De boot wordt gevuld met zand. Bij hoeveel kilogram zand zal de boot voor het eerst zinken?
  11. (3) Een duikboot heeft een volume van 1900 m3. In een duikboot zitten een aantal kamers waar water in en uit gepompt kan worden. Als deze kamers leeg zijn, dan heeft de duikboot een massa van 1 400 000 kg. Hoeveel liter water moet er minimaal in deze kamers worden gepompt als de duikboot wil zinken?
  12. (3) In de onderstaande grafiek kunnen we de luchtdichtheid aflezen bij verschillende hoogten in de atmosfeer.

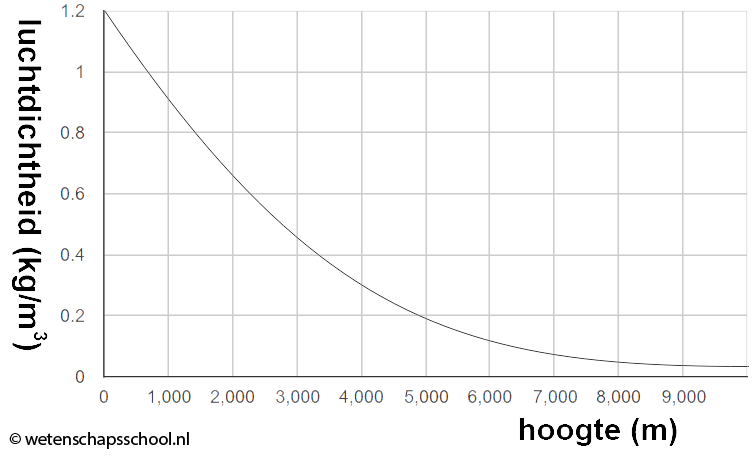    Een persoon gebruikt deze diagram om een schatting te maken hoe hoog hij kan reizen met zijn hete luchtballon. Een hete luchtballon is een grote ballon waarbij de lucht aan de binnenkant verwarmd wordt met een grote vlam.
    1. Leg uit waarom een hete luchtballon bij het verwarmen gaat opstijgen.
    2. De luchtballon heeft een volume (met lucht) van 500 m3 en een massa van 450 kg. Bereken hoe hoog de ballonvaarder maximaal met deze ballon kan komen.
/html>