Met de dichtheid kunnen we o.a. voorspellen of een voorwerp zal zinken of zal drijven in een bepaalde vloeistof. Water heeft bijvoorbeeld een dichtheid van 1000 kg/m3. Als een voorwerp een grotere dichtheid heeft, dan zinkt het in water. Als het een lagere dichtheid heeft, dan blijft het drijven.
Stel dat we een voorwerp met een massa van 2,5 kg en een volume van 1 dm3 in het water gooien. Zal dit voorwerp dan drijven of zinken? Eerst schrijven we het volume om naar SI-eenheden en dan vullen we de formule in: De massa wordt 2,5 kg = 2500 g. Het volume wordt 1 dm3 = 1000 cm3. De dichtheid rekenen we dan als volgt uit:
$$ V = 1 \text{dm}^3 = 0,001 \text{m}^3 $$ $$ \rho = m / V $$ $$ 2,5 / 0,001 = 2500 \text{ kg/m}^3 $$Dit voorwerp heeft dus een dichtheid van 2500 kg/m3. Deze dichtheid is groter dan die van water en dit voorwerp zal dus zinken.
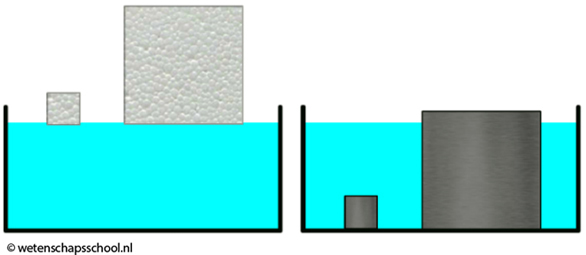
Zoals we hebben gelezen is de dichtheid een stofeigenschap. Een stuk piepschuim heeft dus altijd dezelfde dichtheid, hoe groot of hoe klein dit stuk ook is. Omdat de dichtheid van piepschuim veel kleiner is dan die van water, blijft elk stuk piepschuim drijven. Zelfs als we een gigantisch stuk piepschuim van 500 kg in het water zouden leggen, dan toch blijft het drijven (zie de linker onderstaande afbeelding). Elk stuk ijzer heeft een dichtheid van 7,87 g/cm3. Dit is veel groter dan de dichtheid van water en elk stuk ijzer zal dus zinken. Zelfs al nemen we een stukje ijzer van minder dan een gram, dan toch zal het zinken in water (zie de rechter onderstaande afbeelding).
Hieronder zien we een gigantisch containerschip met een grote massa. Hoe kan het dat dit schip blijft drijven? Dit gaan we begrijpen met het volgende sommetje.

Stel we hebben een stalen plaat van 5m × 10m × 2cm en een massa van 7900 kg. Het volume van de plaat is in dat geval 5 × 10 × 0,02 = 1 m3. De dichtheid wordt dan:
$$ \rho = m / V $$ $$ \small{7900 / 1 = 7900 \text{ kg/m}^3} $$Deze dichtheid is groter dan die van water en dit stuk staal zal natuurlijk zinken.
Nu bouwen we een dun muurtje om de stalen plaat, waardoor de hoogte 16 cm wordt (zie de onderstaande afbeelding).
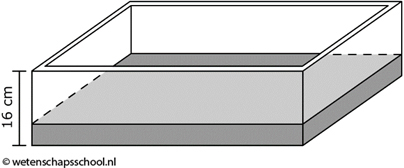
Stel dat het muurtje zelf van een licht materiaal gemaakt is met een massa van 10 kg. Het totale volume is nu 5 × 10 × 0,16 = 8 m3. De totale massa is nu 7 900 + 10 = 7 910 kg. Met deze gegevens kunnen we wederom de dichtheid uitrekenen:
$$\rho = m / V $$ $$ \small{7910 / 8 = 990 \text{ kg/m}^3} $$Deze dichtheid is kleiner dan water en met een muurtje van slechts 16 cm kunnen we dus een stalen plaat van 7900 kg laten drijven! Met behulp van dit principe worden ook de containerschepen ontworpen.
| Stof | Dichtheid (kg/m3) |
|---|---|
| koper | 8960 |
| ijzer | 7870 |
| lood | 11350 |
| aluminium | 2700 |
| kwik | 13534 |
| goud | 19300 |
| vloeibaar water | 998 |
| ijs | 916 |
| vurenhout | 580 |
| glas | 2600 |
| lucht | 1,29 |
- Zorg dat je met behulp van de dichtheid kan bepalen of een stof drijft of zinkt in een vloeistof.
- Zorg dat je begrijpt dat dichtheid een stofeigenschap is en dat dus alle voorwerpen die van een bepaalde stof gemaakt zijn dezelfde dichtheid hebben.
-
In de onderstaande afbeelding zien we dat een moer van ijzer gewoon blijft drijven
op het metaal kwik. Wat zegt dit over de dichtheden van ijzer en kwik? Ga na
of je antwoord klopt met behulp van de tabel in de paragraaf.

- Als je een ijsblokje in een glas water gooit blijft het drijven. Blijft ijs ook drijven in een glas pure alcohol (789 kg/m3)? Leg uit hoe je op je antwoord komt.
-
De zoutconcentratie van de dode zee is erg groot. Dit zorgt ervoor dat mensen hier erg
goed op drijven. Wat zegt dit over het verschil tussen de dichtheid van zoet en zout water?

-
Een voorwerp heeft een volume van 350 mL en een massa van 340 gram.
- Drijft dit voorwerp in water of niet?
- Zonnebloemolie heeft een dichtheid van 0,92 g/cm3. Drijft dit voorwerp in zonnebloemolie of niet?
-
- Een plank heeft een massa van 2 kg. De plank is 2 cm dik, 10 cm breed en 80 cm lang. Bereken of de plank blijft drijven.
- We zagen een kwart van de plank af. Beredeneer of de plank nu blijft drijven.
- Verklaar het antwoord van vraag b.
-
In een experiment in de klas wordt de dichtheid van een leerling bepaald. Eerst wordt met
een weegschaal de massa van de leerling bepaald. De leerling blijft 45 kg te wegen.
Dan wordt er een bak met water de klas in gereden. De bak heeft een lengte van 1m en
een breedte van 60cm. Het water komt 40 cm hoog. De leerling stapt nu in de bak water
en gaat helemaal kopje onder. Als de leerling heeft uitgeademd wordt de nieuwe hoogte
van het water gemeten. Dit blijkt 47,3 cm te zijn. Bereken de dichtheid van de leerling.
- Bereken de dichtheid van de leerling.
- Ga ook na of de leerling drijft of zinkt.
- Had je het antwoord van vraag b verwacht.
- Vul het learning log aan voor deze paragraaf.