Om de kwantumeffecten beter te begrijpen bestuderen het simpelste kwantumsysteem: het deeltje in een doos.

We beginnen met een deeltje dat alleen naar links en rechts kan bewegen in een afgesloten ruimte (zie de onderstaande afbeelding). We noemen dit het deeltje in een doos

Als de doos groot is ten opzichte van de kansgolf van het deeltjes, dan zal de kansgolf zich als een deeltje gedragen. De kansgolf zal dan heen en weer botsen in het doosje alsof het een deeltje is (zie de onderstaande afbeelding).

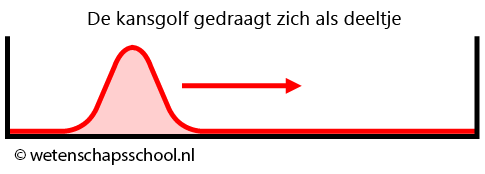
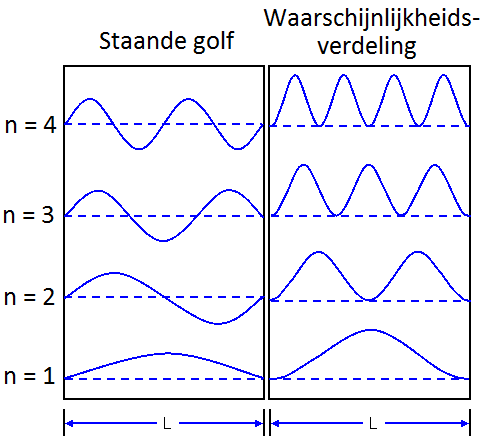
Als de doos echter klein is ten opzichte van de kansgolf, dan beginnen we golfverschijnselen te merken. Als de golf reflecteert tegen de wanden, dan begint deze namelijk met zichzelf te interfereren. Net als bij trillingen in een snaar ontstaat hierbij dan een staande golf met knopen en buiken. Net als bij een snaar geldt dan ook:

$$ L = \frac{1}{2}\lambda n $$ $$\textbf{(twee vaste uiteinden)} $$

In het geval van een deeltje in een doos noemen we n = 1 de grondtoestand en n = 2,3,... de aangeslagen toestanden. Hieronder zien we een aantal toestanden van een deeltje in het doosje. Hoe groter de amplitude van de kansgolf, hoe meer kans dat je het deeltje daar zal aantreffen.

Hieronder leiden we de formule af voor de energie behorende bij elk van deze toestanden:


EXTRA

Als we de formule \( L = \frac{1}{2}\lambda n\) combineren met \(\lambda=h/p\), dan vinden we:

$$ p=nh/2L $$

We kunnen de impuls als volgt relateren aan de kinetische energie:

$$ E_{kin}= \frac{1}{2}mv^2 $$ $$ E_{kin}= \frac{m^2v^2}{2m} $$ $$ E_{kin}= \frac{p^2}{2m} $$

Als we deze formule combineren met \(p=nh/2L\), dan vinden we:

$$ E_n = \frac{n^2h^2}{8mL^2} $$

De kinetische energie van een deeltje in een doosje is dus:

$$ E_n = \frac{n^2h^2}{8mL^2} \;\;\;\;\; \text{(deeltje in doos)} $$
Kinetische energie (En) joule (J)
Energieniveaus (n) -
De constante van Planck (h) 6,62606957 × 10-34 Js
Massa van het deeltje (m) kilogram (kg)
Lengte van de doos (L) meter (m)

Een aantal dingen kunnen we aan deze formule opmerken. Ten eerste zien we dat het elektron in het doosje niet zomaar elke kinetische energie en dus niet elke snelheid kan aannemen. Alleen de waarden die overeenkomen met de staande golven zijn mogelijk. We zeggen in zo'n geval dat de energie en de snelheid gekwantiseerd zijn. Merk ook op dat het niet mogelijk is dat het deeltje geen kinetishe energie en dus geen snelheid heeft. Zelfs in de grondtoestand, de laagste toestand, heeft het deeltje namelijk volgens de formule nog gewoon energie. We noemen dit de nulpuntsenergie. Een deeltje in een doos kan dus niet stilstaan!

Als de doos groot wordt, dan kan je aan de formule zien dat de energieniveau's erg dicht op elkaar komen te liggen. Op een gegeven moment komen deze niveau's zo dicht bij elkaar te liggen dat het lijkt alsof het deeltjes gewoon alle energieniveau's kunnen aannemen. Dit is waarom we in het dageljiks leven niks merken van de kwantisering.

Een deeltje in een doosje kan naar een hoger energieniveau springen door o.a. een foton te absorberen met een energie die precies overeenkomt met het verschil tussen het huidige energieniveau en een hoger niveau. Er geldt dus:

$$ E_{foton} = \Delta E_n$$
Fotonenergie (Ef) joule (J)
Energieverschil tussen twee schillen (ΔE) joule (J)

Hetzelfde geldt als een elektron terugvalt naar een lager niveau. In dat geval komt er juist een foton vrij. Stel dat een elektron in een doosje van 2,0 nm bijvoorbeeld terugvalt van de eerste aangeslagen toestand naar de grondtoestand. Er geldt dan:

$$ E_{foton} = \frac{2^2h^2}{8mL^2} - \frac{1^2h^2}{8mL^2} $$ $$ E_{foton} = \frac{3h^2}{8mL^2} $$ $$ E_{foton} = \frac{3 \times (6,6 \times 10^{-34})^2}{8 \times 9,1 \times 10^{-31} \times (2,0 \times 10^{-9})^2} = 4,5 \times 10^{-20} \text{ J} = 0,28 \text{ eV} $$

Training
    Rekenen met een deeltje in een doosje

  1. Leg uit dat het elektron niet stil kan staan in een doosje.
  2. Een elektron bevindt zich in een afgesloten ruimte van 200 nm in zijn eerste aangeslagen toestand. Bereken de snelheid van het elektron.
  3. Een elektron bevindt zich in een afgesloten ruimte van 200 nm en beweegt met een snelheid van 9,1 × 103 m/s heen en weer. Bereken in welke toestand het deeltje zich bevindt.
  4. Leg uit waarom geldt dat 'Ef = ΔEn'.
  5. Een foton brengt een proton in een doosje van 300 nm lang van de tweede naar de vierde aangeslagen toestand. Bereken de frequentie van het foton dat hiervoor nodig is.
  6. Leg met behulp van een formule uit waarom we er in het dagelijks leven weinig van merken dat elektronen in afgesloten ruimtes slechts bepaalde snelheden kunnen aannemen.
  7. Een elektron in een doosje kan zich ook in meerdere toestanden tegelijk bevinden. In de onderste animatie kan je verschillende toestanden aan en uit zetten. Gebruik deze animatie bij het beantwoorden van de volgende vragen.
    1. Een leerling beweert dat de kansgolf niet verandert in de tijd als het elektron zich in slechts één toestand bevindt. Leg uit of de leerling gelijk heeft.
    2. Een leerling beweert dat de kansgolf zich meer kan gaan gedragen als een deeltje als het elektron zich in een aantal toestanden tegelijk bevindt. Leg uit wat de leerling hier bedoelt.
  8. Met een inktwisser kun je lichtblauwe vulpeninkt onzichtbaar maken. Door de inktmoleculen kan één elektron vrij heen en weer bewegen. Het molecuul kan daarom opgevat worden als een energieput met lengte L. De overgang van de grondtoestand van dit elektron naar de eerste aangeslagen toestand komt overeen met de energie van een foton uit het geel-groene deel van het spectrum met een golflengte van 550 nm. Het molecuul absorbeert deze fotonen. De rest van het licht wordt weerkaatst, dat zie je als lichtblauw.
    1. Bereken uit de geabsorbeerde golflengte de lengte L van de energieput.
    2. De inktwisser zorgt voor de reactie die hieronder is weergegeven:

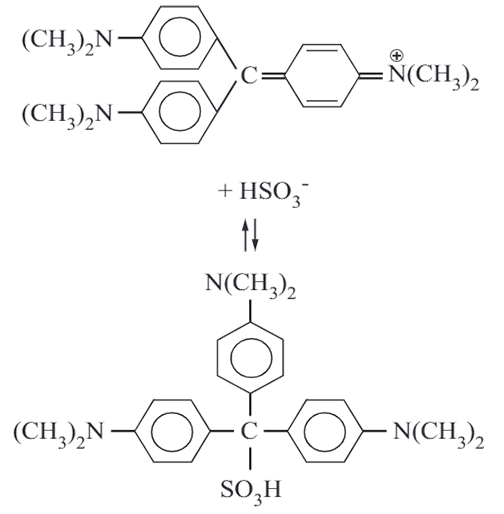      In het molecuul dat ontstaat kunnen de elektronen niet meer langs het centrale koolstofatoom bewegen. Hierdoor is de lengte van de energieput gehalveerd. Het energieverschil tussen de grondtoestand en de eerste aangeslagen toestand wordt daardoor 4 keer zo groot. Leg dit uit.
    3. Het nieuwe molecuul is kleurloos. Leg dit uit met behulp van een berekening en BINAS.
    (bron: examen VWO 2016-pilot)
  9. Een CD-R is een beschrijfbare CD. Deze CD bestaat uit een gladde laag met daarop een bepaalde kleurstof. Bij een onbeschreven CD-R is deze kleurstoflaag doorzichtig. Als je op één plaats de laag verhit, met een korte laserpuls, wordt de kleurstof op die plaats ondoorzichtig zodat er geen licht meer door kan. Door korte pulsen van de schrijflaser kan informatie zo worden weggeschreven in de vorm van doorzichtige en ondoorzichtige 'spots'. Er wordt gebruik gemaakt van cyanine-kleurstoffen. Hieronder staan een aantal van deze moleculen weergegeven.

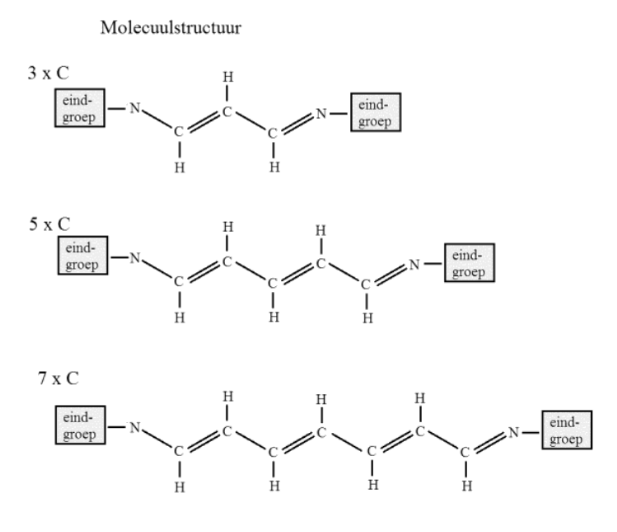    In zo'n molecuul is steeds een aantal vrije elektronen aanwezig. Deze elektronen zitten opgesloten tussen de eindgroepen. Deze opsluiting is te beschrijven als deeltjes in een eendimensionale energieput met lengte L. In de onderstaande diagram is deze lengte uitgezet tegen het aantal C-atomen in de keten.

    In de onderstaande afbeelding zijn de energieniveaus van de elektronen bij vijf verschillende ketenlengtes weergegeven.
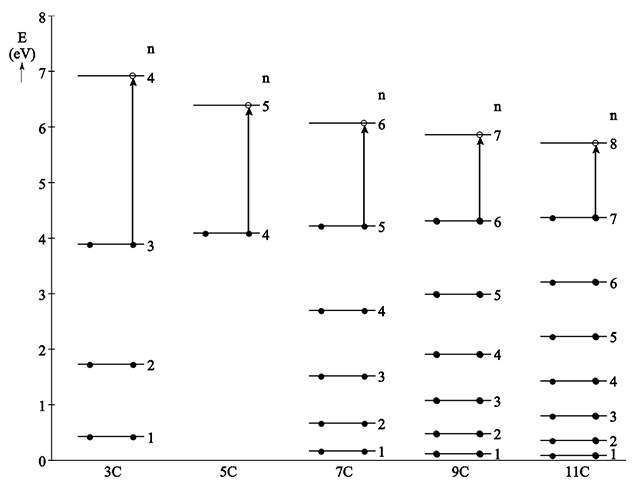
    1. Bij een ketenlengte met 5 C-atomen zijn de niveaus 1, 2 en 3 weggelaten. Bereken de hoogte van de energie van de niveaus 1, 2 en 3 bij een ketenlengte van 5 C-atomen en teken ze in de afbeelding.
    2. Absorptie van licht vindt plaats als een elektron in het hoogste gevulde niveau naar een niveau hoger springt. In de bovenstaande afbeelding is dit aangegeven met pijlen. De CD-R heeft een brand-laser met een golflengte van 800 nm. Bepaal met behulp van de afbeelding welk van deze moleculen daarbij het beste als kleurstof kan worden gebruikt. Licht je antwoord toe met een berekening.
    (bron: examen 2016 voorbeeldopgaven)