In de vorige paragraaf hebben we gezien dat licht uit deeltjes bestaat genaamd fotonen. In deze paragraaf gaan we zien dat licht ook golfeigenschappen hebben. Tevens gaan we zien dat ook massieve deeltjes zoals elektronen zowel golf- als deeltjesverschijnselen hebben.

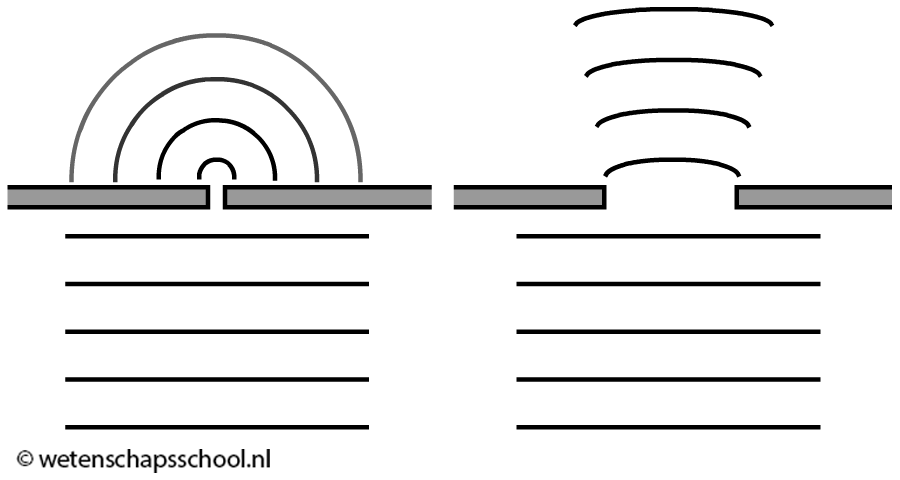
We kunnen als volgt aantonen dat licht ook golfeigenschappen heeft. Als we licht op een plaatje met twee dunne spleetjes schijnen, dan ontstaan achter beide spleet cirkelvormige golven, die met elkaar gaan intereferen (zie de onderstaande afbeelding). We noemen dit het dubbele spleet experiment. Als we achter het scherm een detector plaatsen, dan zien we op dit scherm het maxima en minima zoals we dat ook in het hoofdstuk over geluid gezien hebben.

Als licht alleen deeltjeseigenschappen had gehad, dan hadden we het onderstaande patroon verwacht. Licht zou dan slechts op twee plekken op het scherm te zien zijn. Dit is echter niet het geval. Licht gedraagt zich dus duidelijk als een golf in dit experiment. In één van de opdrachten gaan we leren hoe uit dit patroon de golflengte van het gebruikte licht te bepalen is. Omdat licht dus zowel zowel deeltjes- als golfeigenschappen, spreken we hier van de golf-deeltje-dualiteit.

Later ontdekte men dat deze dualiteit niet alleen geldt voor fotonen, maar voor alle elementaire deeltjes. We kunnen bijvoorbeeld ook elektronen door twee spleten schieten. In de onderstaande afbeelding zien we wat er in dat geval gebeurt. Ten eerste zien we dat de elektronen op specifieke punten op de detector terecht komen. Dit suggereert dat elektronen deeltjes zijn. Maar als we lang genoeg wachten, dan zien we een interferentiepatroon ontstaan. Dit suggereert juist dat elektronen golven zijn. Een dergelijk interferentiepatroon kan alleen ontstaan als elk elektron door beide spleten is gegaan en met zichzelf heeft geinterfereerd! Het moment dat de elektrongolf echter tegen de detector botst, verschijnt het elektron als een puntje op het scherm, alsof het juist een deeltje is! De golf is op dat moment dus ineengeklapt tot een deeltje. Dit lijkt onlogisch, maar toch is dit wat we meten. Dankzij dit vreemde resultaat, zei de bekende kwantumfysicus Niels Bohr: 'wie zegt de kwantumfysica te begrijpen, heeft het niet begrepen'.

Maar wat bepaalt dan waar het elektron terecht komt op de detector? Dit blijkt niet te voorspellen te zijn. Het is niet mogelijk van te voren uit te vinden waar het elektron op het scherm zal komen. Het enige dat we weten is dat als je genoeg elektronen afschiet, dat dan een voorspelbaar interferentiepatroon ontstaat. Bij de maxima is de kans op een elektron het grootst en bij de minima is er geen kans het elektron te vinden. De kwantumfysica is dus gebaseerd op kans en het interferentiepatroon geeft ons hoe groot deze kans is. We noemen dit patroon dan ook een waarschijnlijkheidsverdeling. We gebruiken voor deze kansverdeling ook wel het symbool P(x), waarbij de x aangeeft dat de kans P afhankelijk is van de plaats x waar gemeten wordt. Hieronder zien we een afbeelding van de waarschijnlijkheidsverdeling die bij dit experiment hoort:

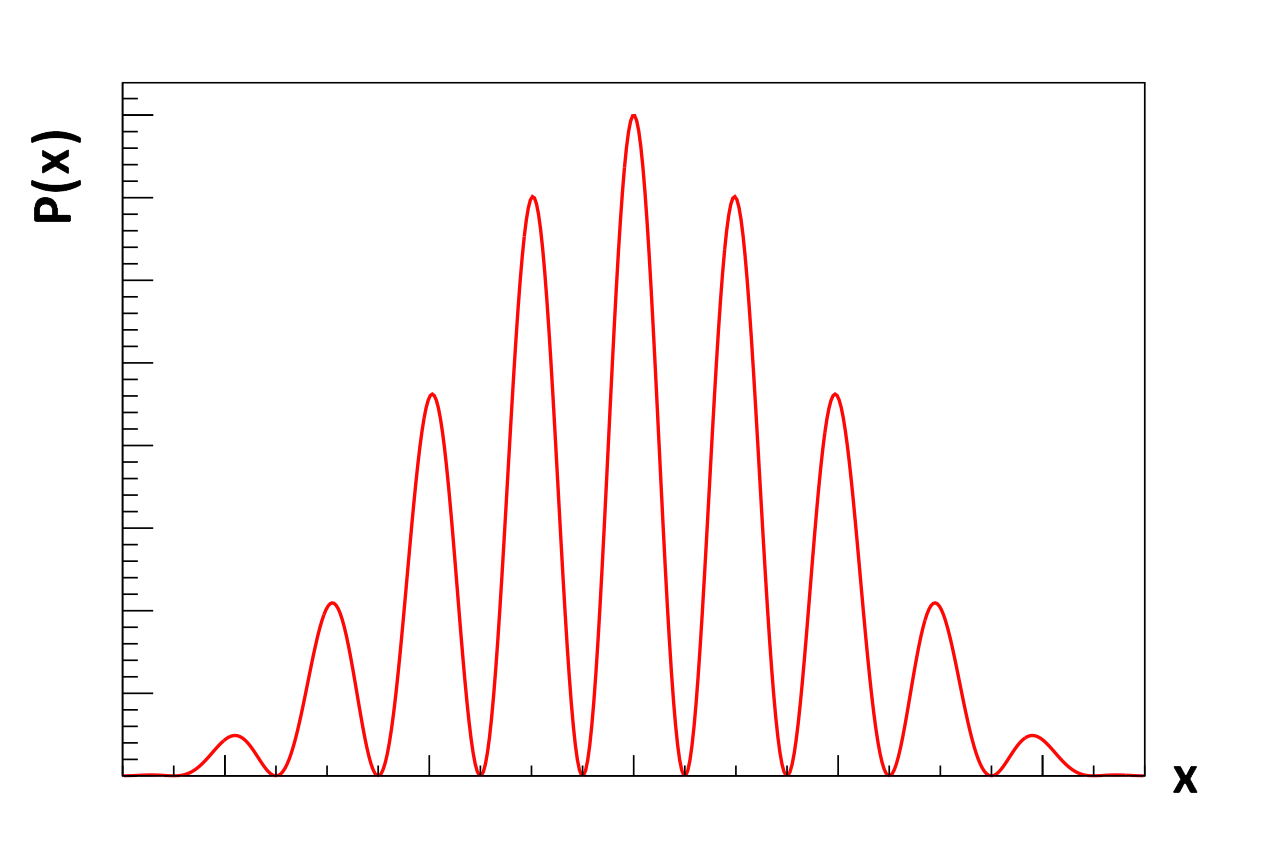
Als je de kans wil vinden dat je een elektron in een bepaald gebiedje zal aantreffen, dan doe je dat door de oppervlakte onder de grafiek te berekenen. Het totale oppervlak onder de grafiek is dus altijd 1. Dit komt namelijk overeen met 100%. Je hebt immers 100% kans dat het elektron ergens in de gehele ruimte terecht komt.

Als een elektron dus een golf is, dan moet het ook een golflengte hebben. De wetenschapper Louis de Broglie vond één formule voor de golflengte van alle deeltjes. We noemen deze golflengte de debroglie-golflengte. Er geldt:

$$ \lambda = \frac{h}{p} $$

De debroglie-golflengte (λ)	meter (m)
De constante van Planck (h)	6,62606957 × 10^-34 Js
Impuls (p)	kilogram keer meter per second (kgm/s)

De impuls wordt voor deeltjes met massa gegeven door:

$$ p = mv $$

Impuls (p)	kg m/s
Massa (m)	kilogram (kg)
Snelheid (v)	meter per seconde (m/s)

Hieronder wordt de formule voor de debroglie-golflengte afgeleid:

EXTRA

In het hoofdstuk over relativiteitstheorie hebben we gevonden dat voor deeltjes zonder massa (zoals fotonen) geldt dat:

$$ p = \frac{E}{c} $$

Impuls (p)	kg m/s
Energie (E)	joule (J)
Snelheid van het licht (c)	3,0 × 10⁸ m/s

Als we deze formule combineren met E_f = hf, dan vinden we:

$$ p = h\frac{f}{c} $$

In het hoofdstuk over geluid hebben we gezien dat λ = v/f. Als we deze formule gebruiken, met voor v de lichtsnelheid c, dan vinden we:

$$ p = \frac{h}{\lambda} $$

Later bleek uit experimenten dat deze formule behalve voor fotonen ook voor andere deeltjes geldig was.

In het dagelijks leven merken we weinig van de golfeigenschappen van deeltjes. Dit komt omdat omdat h in de formule van de Broglie zo klein is. Aan de formule λ = h/p zien we dat de golflengte alleen groot wordt als de impuls (p) erg klein is. Dit gebeurt bijvoorbeeld als we een stof extreem koud maken. In dat geval wordt de snelheid en dus ook de impuls van de deeltjes klein.

De formule van de Broglie speelt o.a. een rol in de microscopie. Om dit te begrijpen moeten we eerst het begrip buiging begrijpen. Golven buigen namelijk om voorwerpen heen. Bij geluid kennen we dit effect allemaal. We kunnen bijvoorbeeld iemand horen die om een hoek staat, omdat het geluid de hoek om buigt.

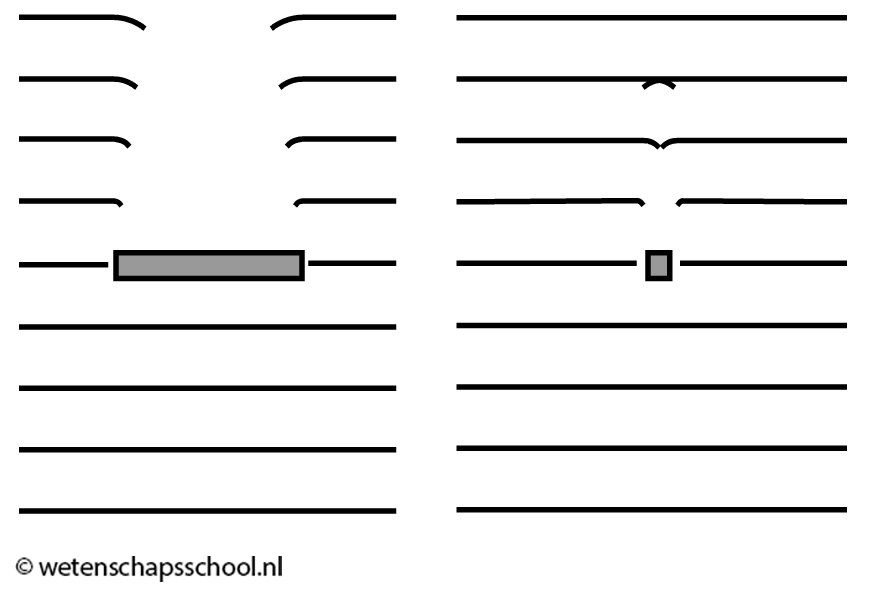
Hieronder zien we golven die zich door een dunne en een brede spleet bewegen. Als de spleet klein is ten opzichte van de golflengte, dan treedt veel buiging op. Zo niet, dan treedt juist weinig buiging op. Bij een erg brede spleet vindt bijna helemaal geen buiging plaats. Dankzij de kleine golflengte van zichtbaar licht, merken we weinig van het buigen van licht in het dagelijks leven. Voor radiogolven is dit echter een ander verhaal. Radiogolven hebben een veel grotere golflengte en buigen daarom gemakkelijk om alledaagse voorwerpen heen. Dit is waarom een radio bijna overal ontvangst heeft. Het licht buigt zich om alle voorwerpen heen en komt zo in alle uithoeken terecht.

In de onderstaande afbeelding wordt een voorwerp beschenen met licht. Ook hier treedt buiging op. Als het voorwerp klein is ten opzichte van de golflengte, dan treedt veel buiging op. Zo niet, dan vindt weinig buiging op. Links in de afbeelding treedt dus weinig buiging op en als gevolg is er achter het voorwerp een duidelijke schaduw te zien. Rechts is de buiging zo extreem dat de golven hun pad vervolgen alsof er helemaal geen voorwerp aanwezig is.

Dit effect zorgt voor een limiet in het gebruik van lichtmicroscopen. Als de golflengte van zichtbaar licht groter is dan het voorwerp dat bekeken wordt, dan krijg je door buiging geen goed beeld. Bij erg kleine voorwerpen moet dus een andere type microscoop gebruikt worden. Een voorbeeld is een elektronenmicroscoop. Stel dat de elektronen in dit type microscoop met een snelheid van 2,3 × 10⁵ m/s worden afgeschoten op het voorwerp dat we willen bekijken, dan vinden we de volgende debroglie-golflengte:

$$ \lambda = \frac{h}{mv} $$ $$ \small{\frac{6,63\times 10^{-34}}{9,31\times 10^{-31} \times 2,3 \times 10^5}=3,0 \;\text{nm} } $$

Dit is klein genoeg om bijvoorbeeld een virus te kunnen bekijken, hetgeen met een normale microscoop niet mogelijk is.

Training

Redeneren met buiging en interferentie

Als je je hand onder zonlicht houdt, dan ontstaat op de ondergrond een scherpe schaduw. Wat zegt dit over de golflengte van zonlicht? Gebruik in je antwoord het woord buiging.
Een paal staat in de zee. Als golven met een golflengte van een paar meter langskomen, dan worden de golven even vervormd door de aanwezigheid van de paal, maar even later gaan de golven verder alsof de paal er niet geweest was. Leg uit hoe dit kan.
Leg uit waarom radiogolven geschikt zijn voor het ontvangen van wifi.
Leg uit hoe wetenschappers hebben aangetoond dat deeltjes zoals elektronen en fotonen zowel een golf- als een deeltjeskarakter hebben.
In de onderstaande afbeelding zien we een golf die aankomt bij een plaat met daarin twee spleten. Achter de spleten onstaan er bij elke spleet een cirkelvormige golf. Recht achter de twee spleten komen de golven in fase aan. Hier bevindt zich dus een maximum. Het eerst volgende maximum vindt plaats bij punt P. Rechts zien we een close-up van de twee golven die aankomen in punt P.
1. Laat zien dat voor de maxima geldt dat: $$ n\lambda = d\sin{\theta} $$ n is een heel getal onder de hoeken θ waar zich een maximum bevindt.
2. De afstand tussen de spleten is 1,43 μm. Laat met een bepaling zien dat de golflengte van het licht 567 nm is. Je mag aannemen dat de afbeelding op schaal is afgebeeld.
3. Welke kleur heeft dit licht?
4. Bepaal hoeveel maxima er maximaal achter het scherm te vinden zijn.

Redeneren met de kansverdeling

In de onderstaande afbeelding is schematisch een waterstofjodide-atoom afgebeeld. Het waterstofatoom trilt heen en weer. In de afbeelding zien we een klassieke kansverdeling waaruit de kans kan worden afgelezen dat het waterstofatoom zich op een bepaalde plek bevindt.
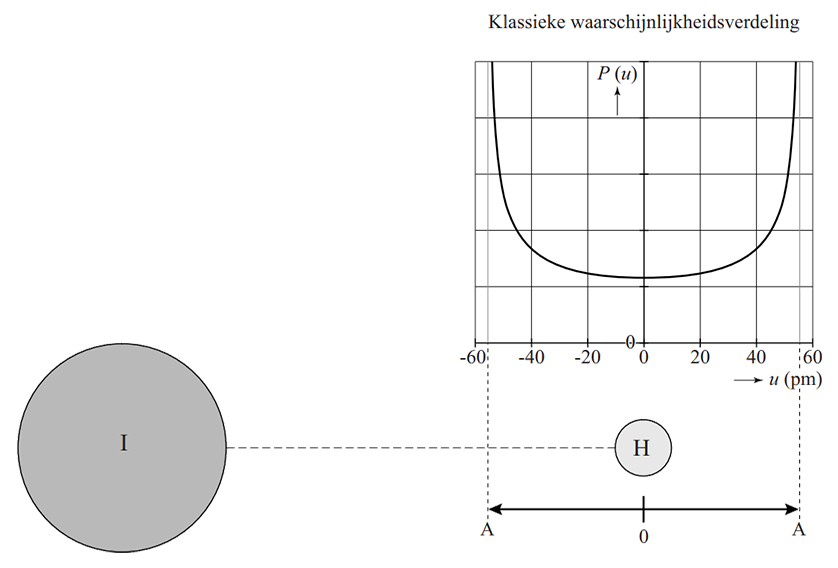
1. Leg uit waarom P(u) een minimum heeft voor u = 0 en een maximum voor u = ±A.
2. Leg uit hoe de waarschijnlijkheidsverdeling P(u) in breedte en hoogte verandert als de totale energie van de trilling groter wordt.

Rekenen met de debroglie-golflengte

Laat met een berekening zien dat een virus van 250 nm niet met zichtbaar licht waargenomen kan worden door een telescoop.
Met een elektronenmicroscoop kunnen kleinere voorwerpen zichtbaar worden gemaakt dan met een lichtmicroscoop.
1. Leg uit waarom dit het geval is.
2. Elektronen worden met een snelheid van 2,3 × 10⁵ m/s op een virus geschoten ter grootte van 150 nm. Ga met een berekening na of het mogelijk om hiermee het virus te bekijken.
3. Bereken of het mogelijk is om met deze microscoop een watermolecuul ter grootte van 0,15 nm zichtbaar te maken.
In 1923 deed Louis de Broglie de veronderstelling dat deeltjes een golfkarakter vertonen en dus een golflengte bezitten. In 1927 toonden Clinton Davisson en Lester Germer experimenteel aan dat de veronderstelling van De Broglie juist was. Davisson en Germer gebruikten de opstelling die hieronder schematisch is weergegeven. Weergegeven is een elektronenbundel die versnelt wordt door een versnelspanning U. De bundel komt terecht op een nikkelplaatje. Elektronen die reflecteren tegen het plaatje kunnen worden opgevangen door een detector. Deze kan verdraaid worden rondom het nikkelplaatje.

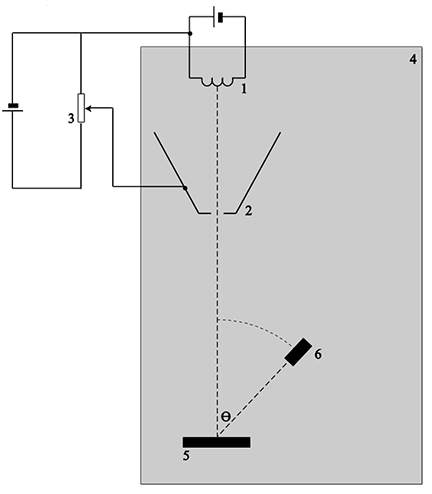De afstand tussen (het midden van) het plaatje en de detector blijft daarbij gelijk. De detector vangt de elektronen op die terugkomen met een hoek θ ten opzichte van de invallende bundel. Hieronder staan de meetresultaten van dit experiment bij verschillende hoeken.
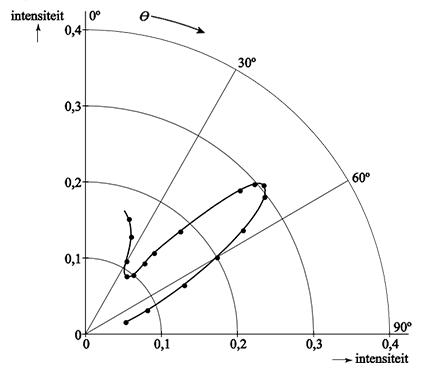
1. Leg, aan de hand de bovenstaande afbeelding, uit dat elektronen zich hier gedragen als golven.
2. Leg uit of dit patroon ook zichtbaar zou zijn als de elektronenbundel één voor één een elektron zou kunnen afschieten.
3. In de onderstaande afbeelding staat schematisch het principe weergegeven van het terugkomen van de elektronengolven van het nikkel. De punten geven de nikkelatomen weer. De afstand d is de afstand tussen de atomen.
  
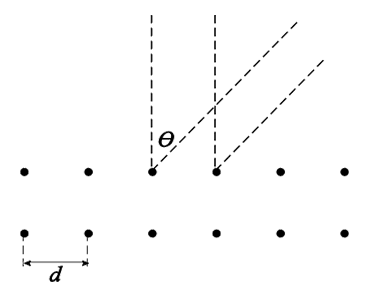  De meetresultaten van Davisson en Germer kunnen worden beschreven met: $$ n\lambda = d\sin{\theta} $$ n is hier een heel getal bij de hoeken θ waarbij een maximum optreedt. Leid deze formule af.
4. Vanuit de situatie in de opstelling kan de debroglie-golflengte van de elektronen berekend worden met de formule: $$ \lambda = \frac{h}{\sqrt{2meU}} $$ U is hier de versnelspanning, waarmee de elektronen versneld zijn. Leid deze formule af uit formules in BINAS. Laat hiervoor eerst zien dat: $$ E_{kin} = \frac{p^2}{2m} $$
5. Uit de meetresultaten van Davisson en Germer is de afstand d te bepalen. Bepaal de afstand d. Ga hier uit van een versnelspanning van 54 V.
(bron: examen 2016 voorbeeldopgaven)
Een onderzoeken schiet positronen op een stuk aluminium. In het metaal worden de positronen afgeremd totdat ze nog een energie van 0,040 eV over hebben. De positronen blijven dan vrij doorbewegen in het metaal, totdat ze botsen tegen elektronen in het metaal. De twee deeltjes annihileren dan en hierbij ontstaat twee fotonen. Hoe lang het duurt voordat het positron annihileert, noemen we de levensduur van het positron.
De afstand tussen de atomen in het metaalrooster van aluminium is 0,41 nm. Bereken met hoeveel roosterafstanden de debroglie-golflengte van de vrije positronen in het metaal overeenkomt.
(bron: examen 2016 voorbeeldopgaven)