In deze paragraaf gaan we het uitrekken van voorwerpen bestuderen. We gebruiken hiervoor o.a. de begrippen spanning en rek.

Als we een kracht op een voorwerp uitoefenen, dan gaat dit voorwerp vervormen. Denk bijvoorbeeld aan het uitrekken van een elastiek. Om dit proces te begrijpen hebben we het begrip spanning nodig. We berekenen de spanning in een kabel als volgt:

$$ \sigma = \frac{F}{A} $$
Spanning (σ) pascal (Pa) of newton per vierkante meter (N/m2)
Kracht (F) newton (N)
Doorsnede (A) vierkante meter (m2)

De doorsnede (A) is een oppervlak gemeten vierkante meter. Dit is het oppervlak dat je ziet als je de kabel zou doorsnijden. Met de onderstaande formules kunnen we met de doorsnede de diameter (d) en de straal (r) uitrekenen:

$$ A = \pi r^2 $$ $$ d = 2r $$

Een maat voor hoeveel een voorwerp uitrekt is de rek (ook wel relatieve rek genoemd):

$$ \epsilon = \frac{\Delta l}{l_0} $$
Rek (ε) -
Uitrekking (Δl) meter (m)
Originele lengte (l0) meter (m)

De rek geeft ons de fractie die het materiaal langer is geworden door er een kracht op uit te oefenen. Als we de rek vermenigvuldigen met 100, dan vinden we hoeveel procent het materiaal langer is geworden. Een rek van 0,25 betekent dus dat de kabel 25 procent langer is geworden.

Bij een kleine kracht zal een voorwerp na het uitoefenen van een kracht weer terugschieten naar zijn originele lengte. We spreken hier van elastische vervorming. Dit gebeurt bijvoorbeeld als we een elastiekje een klein stukje uitrekken en weer loslaten.

Zolang materiaal elastisch vervormd, geldt:

$$ E = \frac{\sigma}{\epsilon} $$
Elasticiteitsmodulus (E) newton per vierkante meter (N/m2)
Rek (ε) -
Spanning (σ) pascal (Pa) of newton per vierkante meter (N/m2)

Na het uitoefenen van een te grote kracht zal het voorwerp niet meer terugschieten naar zijn oorspronkelijke vorm. In dit geval spreken we van plastische vervorming.

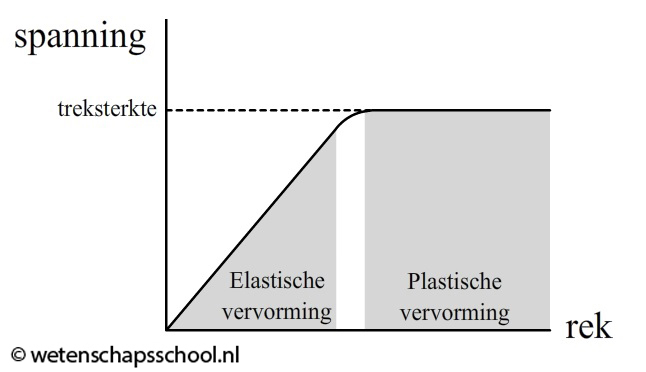
In een (spanning,rek)-diagram is de overgang van elastische naar plastische vervorming goed te zien. Zolang de grafiek een recht evenredig verband laat zien (een recht lijn door de oorsprong), spreken we van elastische vervorming. In alle andere gevallen vindt plastische vervorming plaats. De vorm van dit plastische deel is erg afhankelijk van de stof. De maximale spanning die het voorwerp aan kan noemen we de treksterkte.

In het onderstaande diagram zien we twee grafieken van twee soorten kabels die worden uitgerekt. Het materiaal dat hoort bij de rode grafiek kan flink uitgerekt worden voordat plastische vervorming optreedt. We noemen dit voorwerp daarom ook wel elastisch. Een voorbeeld hiervan is een bungeekoord. Het andere materiaal kan maar een klein beetje worden uitgerekt voordat plastische vervorming optreedt. Dit materiaal is dus niet elastisch. Een voorbeeld hiervan is een stukje kauwgom. Als we een stukje kauwgom vervormen, blijft het direct in zijn nieuwe vorm staan.




Training
    Rekenen met de formules voor de spanning, de rek en de elasticiteitsmodulus
  1. De eenheid van de spanning is de pascal. Laat met behulp van de formule zien dat dit ook te schrijven is als N/m2.
  2. Vind met behulp van de formule de eenheid van de rek.
  3. Vind met behulp van de formule de eenheid van de elasticiteitsmodulus.
  4. Een blok met massa m en een blok met massa 2m hangen elk aan een kabel met dezelfde eigenschappen. Vergelijk de spanning, de rek en de elasticiteitsmodulus in de kabels.
  5. Aan twee kabels hangt elk een blok met massa m. Beide kabels zijn van hetzelfde materiaal gemaakt, hebben dezelfde lengte, maar hebben een andere diameter. Vergelijk de spanning, de rek en de elasticiteitsmodulus in de kabels.
  6. Een lift met een massa van 300 kg mag maximaal 800 kg aan massa vervoeren. De lift hangt aan een stalen kabel. Zonder belasting is de kabel 20 meter lang. Met maximale belasting wordt de kabel 0,50 cm langer.
    1. Bereken de spanning in de liftkabel.
    2. Bereken de diameter van de liftkabel bij maximale belasting.
  7. Als een spaak in het fietswiel wordt gemonteerd, wordt de spaak ook gespannen. Dit wordt voorspannen genoemd. Een bepaalde roestvrijstalen spaak krijgt een spanning van 190 MPa. De doorsnede van de spaak is 2,63 mm2.
    1. Bereken de spankracht in de voorgespannen spaak.
    2. Bereken hoeveel procent de voorgespannen spaak is uitgerekt.
  8. Tijdens het springen oefent een kangoeroe een maximale spanning van 27 MPa uit op de pees van de spier waarmee de kangoeroe afzet tegen de grond. De pees rekt daarbij 2,5% uit. De uitrekking van de pees is (vrijwel) lineair. Bereken de elasticiteitsmodulus van de pees.
    (bron: examen HAVO 2015-1)
  9. In de film Spiderman 2 stopt de held Spiderman een op hol geslagen trein met behulp van draden gesponnen uit spinrag.

    Engelse natuurkundestudenten van de Universiteit van Leicester hebben berekend of het spinrag van een gewone spin hiervoor sterk genoeg is. Als de draden maximaal zijn uitgerekt, is de spankracht in de linkerdraad 1,8 x 105 N. De rek van het spinrag van Spiderman is dan 40. Uit de film blijkt dat elk van de twee draden van het spinrag van Spiderman bestaat uit acht losse draden. De diameter van een van deze acht draden is 5,0 mm. De diameter is tijdens het remmen constant. Het sterkste spinrag dat in de natuur wordt gevonden, heeft een elasticiteitsmodulus van 12 GPa bij een rek van 40.
    Leg met behulp van een berekening van de spanning uit of het spinrag dat in de natuur wordt gevonden minder sterk is dan, even sterk is als, of sterker is dan het spinrag van Spiderman.
    (bron: examen HAVO 2015-2)
  10. Beschrijf wat een relatieve rek van 0,20 betekent.
    11. Interpreteren van een(spanning,rek)-diagram
  11. Bestudeer het onderstaande diagram:

    1. Geef in het onderstaande diagram aan waar elastische vervorming en waar plastische vervorming plaatsvindt.
    2. Geef aan in welk gebied de formule voor de elasticiteitsmodulus geldt.
    3. Geef ook in de grafiek de treksterkte van het materiaal aan.
    (bron: examen HAVO 2015-1)
  12. In het onderstaande diagram wordt de relatie tussen de spanning en de rek van twee verschillende stoffen vergeleken.

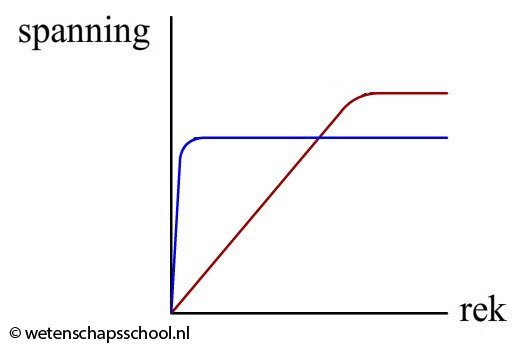
    1. Welke stof breekt het snelst? Leg je antwoord uit.
    2. Welke stof is het meest elastisch? Leg je antwoord uit.
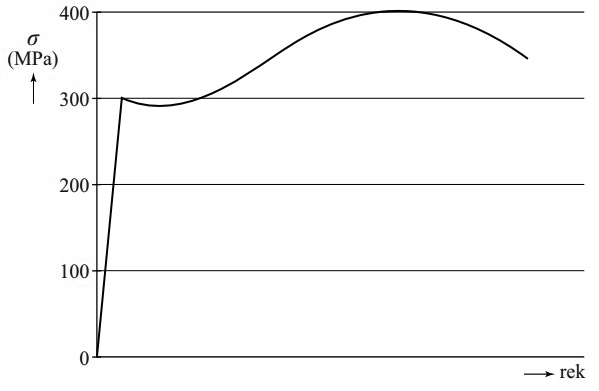
  13. De draagkabel van een kabelbaan is gemaakt van staal en heeft een doorsnede van 3,85 × 103 mm2. In de onderstaande afbeelding is het (spanning,rek)-diagram weergegeven van de gebruikte staalsoort. Bepaal de maximale spankracht die deze draagkabel kan uitoefenen zonder blijvend te vervormen.

    (bron: examen HAVO 2015-1)
  14. Een stretchsensor is een sensor die wordt gebruikt om een lichaamsbeweging om te zetten in een computerbeeld. Een stretchsensor bevat een strookje rekbaar materiaal, waarvan de elektrische weerstand verandert als het wordt uitgerekt.

    Hieronder is een (spanning,rek)-diagram van het rekbare materiaal weergegeven:

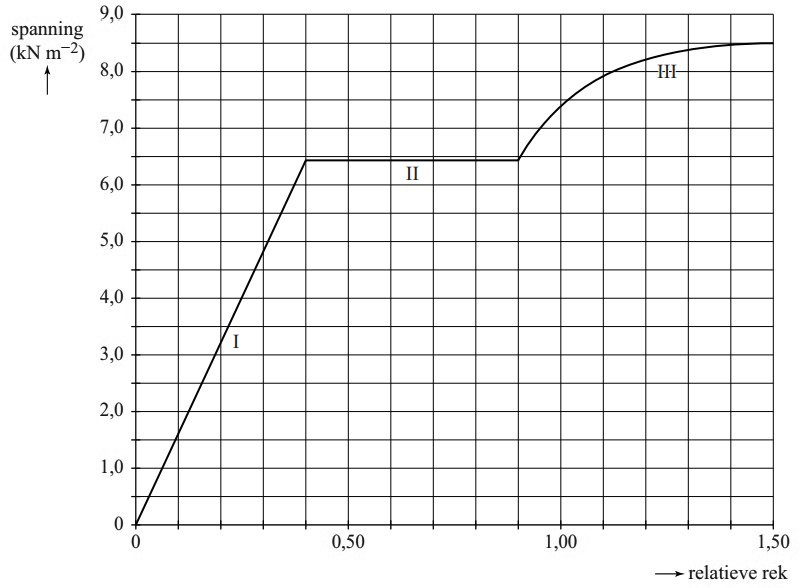
    1. Geef voor elk deel van de grafiek aan of er geen vervorming, elastische vervorming of plastische vervorming plaatsvindt.
    2. Bepaal met behulp van het diagram de elasticiteitsmodulus van het materiaal.
    3. De sensor mag de lichaamsbeweging niet hinderen. De kracht die nodig is voor het uitrekken van het materiaal moet dus klein zijn. Bij het uitrekken krijgt het materiaal op een gegeven moment een rek van 0,20. De doorsnede van het rekbare materiaal is 1,8 mm2. Bepaal de kracht waarmee dan aan het materiaal getrokken wordt.
    (bron: examen HAVO 2017-2)