In het onderstaande (x,t)-diagram is de snelheid niet constant. Op elk tijdstip hebben we hier dus een andere snelheid. Als we bijvoorbeeld de snelheid op tijdstip A willen bepalen, dan kunnen we dit doen door een klein driehoekje te tekenen en hiermee de snelheid te berekenen (zie de linker afbeelding). Dit is echter lastig meten en levert daardoor een zeer onnauwkeurig antwoord op. We kunnen dit probleem oplossen door het kleine lijnstukje in beide richtingen zoveel mogelijk te verlengen (zie de rechter afbeelding). De verlengde lijn noemen we een raaklijn. Omdat de raaklijn net zo steil loopt als het oorspronkelijke lijntje vinden we hier dezelfde snelheid.

De snelheid op tijdstip A is in dit geval gelijk aan: $$ v = \frac{4,0}{6,0} = 0,67 \text{ m/s} $$ Er geldt dat hoe steiler de raaklijn loopt, hoe groter de snelheid is.

We kunnen iets soortgelijks doen in een (v,t)-diagram. In dit type diagram is de raaklijn gelijk aan de versnelling op een specifiek tijdstip.

De versnelling op tijdstip A is in dit geval gelijk aan: $$ a = \frac{4,0}{6,0} = 0,67 \text{ m/s}^2 $$ Er geldt hier dat hoe steiler de raaklijn loopt, hoe groter de versnelling is.

---

Bepalen van de snelheid op een tijdstip met een raaklijn

---

1. (3,4) Bereken de snelheid op tijdstip t = 2,0 s:
   
2. (3,4) Bereken de snelheid op tijdstip t = 5,0 s.
   
3. (3,4) Bereken de beginsnelheid, de eindsnelheid en de snelheid op tijdstip t = 3,0 s.
   
4. (3,4) In het onderstaande diagram wordt de beweging van een bal beschreven die over de grond rolt en tot stilstand komt. Op tijdstip t = 0 s werd de bal losgelaten. Wat was de beginsnelheid van de bal?
   
5. (3,4) Bereken de maximale snelheid in het volgende diagram:
   
6. (3,4) Beschrijf hoe je de snelheid kan bepalen op een specifiek moment met behulp van een (x,t)-diagram.
7. (3,4) Bereken de versnelling op tijdstip t = 20 s:
   
8. (3,4) Hieronder is de beweging van een optrekkende auto beschreven. Bereken de maximale versnelling en de maximale snelheid tijdens de beweging.
   
9. (3,4) Bereken de versnelling op tijdstip t = 1,0 s en t = 4,0 s.
   
10. (3,4) Hieronder is het (v,t)-diagram weergegeven van de beweging van een jojo. Op tijdstip t = 0 is het koord volledig om de jojo gewikkeld en laat de persoon de jojo los.
    
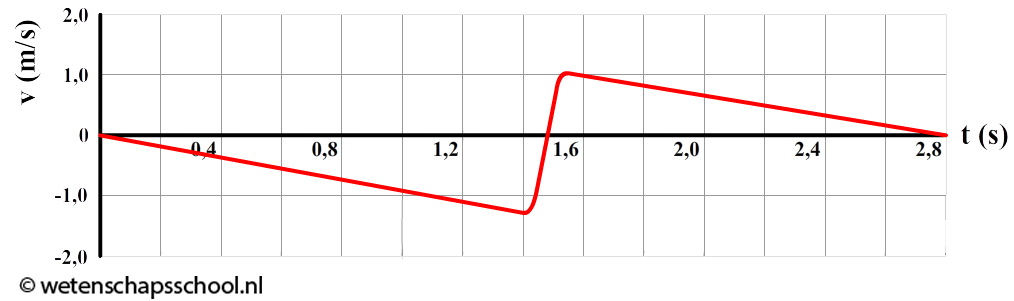
    1. Leg uit op welk moment de jojo op zijn laagste punt is.
    2. Bereken de lengte van het koord.
    3. Op het laagste punt ondergaat de jojo een plotselinge versnelling waarbij de jojo van richting verandert. Geef de versnelling waarmee dit gebeurt.