In dit hoofdstuk gaan we beweging beschrijven met behulp van zowel grafieken als formules. We beginnen deze paragraaf met het (x,t)-diagram met op de horizontale as de tijd en op de verticale as de positie. Daarna gaan we met deze grafiek de snelheid te bepalen. In de bovenbouw leren we de snelheid op een tijdstip te bepalen met behulp van een raaklijn.

In dit hoofdstuk gaan we het bewegen van voorwerpen bestuderen. Een manier om beweging te beschrijven is met een (x,t)-diagram. Dit is een diagram met op de horizontale as de tijd (t) en op de verticale as de positie (x). In het onderstaande (x,t)-diagram zijn bijvoorbeeld twee auto's beschreven die van Amsterdam naar Utrecht rijden.

Merk op dat auto A eerder in Utrecht aankomt. Auto A moet dus een grotere snelheid hebben dan auto B. In een (x,t)-diagram geldt dus:

$$ \text{steiler} = \text{sneller} $$

Laten we dit principe een paar keer toepassen. Links zien we een grafiek die horizontaal loopt. De positie x verandert hier niet in de tijd. Het voorwerp staat hier dus stil. Rechts zien we een voorwerp dat zich geleidelijk verplaatst. Elke seconde wordt er evenveel meter afgelegd. We spreken hier van een constante snelheid of een eenparige beweging.

Links zien we een grafiek die steeds steiler gaat lopen. We hebben hier dus te maken met een versnelling. Rechts zien we een grafiek die steeds minder steil gaat lopen. Hier hebben we dus te maken met een vertraging.



De snelheid van een voorwerp kunnen we als volgt berekenen:

$$\frac{\Delta x}{\Delta t} = v$$
Verplaatsing (Δx) meter (m)
Tijdsduur (Δt) seconde (s)
Snelheid (v) meter per seconde (m/s)

Het Δ-teken staat voor 'de toename van'. Δx staat dus voor de toename van de positie x. Neem bijvoorbeeld de onderstaande grafiek. We zien hier dat een voorwerp is verplaatst van x = 1 meter naar x = 5 meter. De toename van de positie is in dit geval dus 5 - 1 = 4m. We hebben hier de eindpositie min de beginpositie gedaan. In wiskundetaal geldt dus:

$$ \Delta x = x_{eind} - x_{begin} $$

De verplaatsing (Δx) is in het bovenstaande diagram dus 4 meter. De tijdsduur (Δt) van de beweging is 6 seconden. De snelheid is dus gelijk aan:

$$ \frac{\Delta x}{\Delta t} = v$$ $$ \frac{4,0}{6,0} = 0,67 \text{ m/s}$$

Laten we nog een tweede voorbeeld bespreken. In het onderstaande diagram is de verplaatsing:

$$ \Delta x = x_{eind} - x_{begin} = 30 - 40 = -10m $$

Het minteken geeft aan dat de positie x is afgenomen in de tijd.

De snelheid wordt in dit geval:

$$ \frac{-10}{30} = -0,33 \text{ m/s} $$

De negatieve snelheid geeft aan dat het voorwerp achteruit is bewogen.


Klas 4
In het onderstaande diagram is de snelheid niet constant. Op elk tijdstip hebben we hier dus een andere snelheid. Als we bijvoorbeeld de snelheid op punt A willen bepalen, dan kunnen we dit doen door een klein driehoekje te tekenen en hiermee de snelheid te berekenen (zie de linker afbeelding). Dit is echter lastig meten en levert daardoor een zeer onnauwkeurig antwoord op. We kunnen dit probleem oplossen door het kleine lijnstukje in beide richtingen zoveel mogelijk te verlengen (zie de rechter afbeelding). De verlengde lijn noemen we een raaklijn. Omdat dat raaklijn net zo steil loopt als het oorspronkelijke lijntje vinden we hier dezelfde snelheid.


De snelheid in punt A is in dit geval gelijk aan: $$ \frac{4,0}{6,0} = 0,67 \text{ m/s} $$





Training
    Herkennen van bewegingen in een (x,t)-diagram.
  1. Behaal 15 punten:
  2. Beschrijf de beweging van de voorwerpen in de volgende (x,t)-diagrammen.

    3. Schetsen van bewegingen in (x,t)-diagrammen.
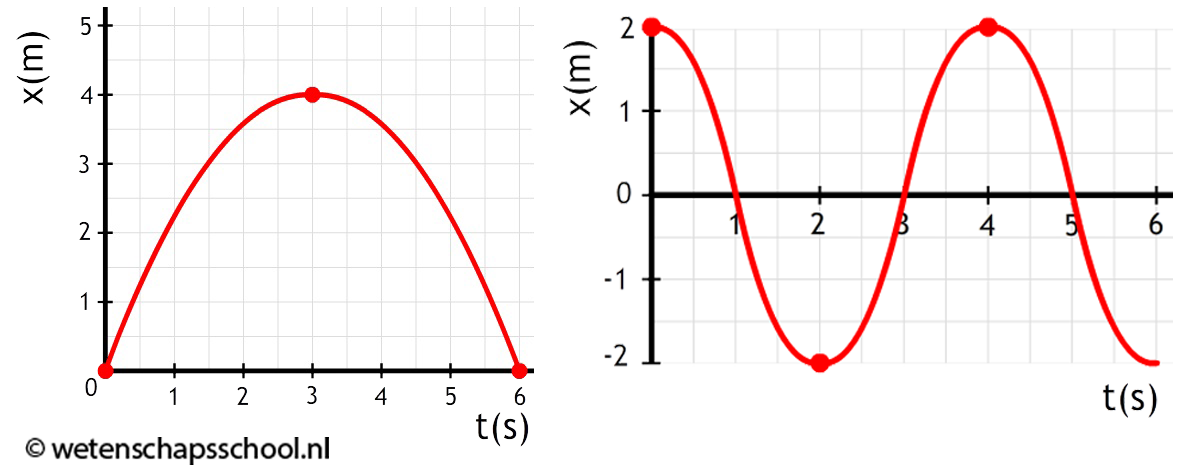
  3. Schets de volgende (x,t)-diagrammen:
    1. Mario gaat een tijdje met constante snelheid vooruit. Dan gaat hij versnellen.
    2. Mario staat eerst stil, maar dan gaat hij steeds sneller rennen. Als hij zijn gewenste snelheid bereikt heeft rent hij met constante snelheid verder.
    3. Mario rent even met constante snelheid. Dan gaat hij steeds langzamer rennen tot hij stil staat. Hij blijft dan even uitrusten, maar daarna gaat hij weer versnellen.
    4. Mario gooit zijn pet recht omhoog de lucht in. Uiteindelijk valt de pet op de grond.
    5. Mario laat zijn pet uit zijn hand vallen. Uiteindelijk valt de pet op de grond.
  4. Noteer waar je op moet letten bij het aflezen van een (x,t)-diagram. Hoe herken je stilstand, constante snelheid, versnelling en vertraging. En hoe herken je vooruit en achteruit bewegen. Beschrijf dit in volledige zinnen in het online logboek. Zijn er nog andere dingen die je wilt onthouden voor de toets? Schrijf deze dan ook op.


    5. Bepalen van de snelheid met behulp van een (x,t)-diagram.
  5. Bereken de snelheid van de voorwerpen die in de volgende (x,t)-diagrammen beschreven zijn. Laat hier ook duidelijk zien of de snelheid positief of negatief is.
  6. Hieronder zien we het (x,t)-diagram die de beweging van een parachutespringer beschrijft. De x staat hier voor de hoogte van de springer.
    1. Op welke hoogte werd de parachute geopend? Leg uit hoe je dit weet.
    2. Wat is de beginsnelheid van de springer geweest?
    3. Bereken de maximale snelheid die de springer bereikt. Leg uit hoe je dit berekent.
  7. Noteer hoe je de snelheid bepaalt in een (x,t)-diagram. Beschrijf de stappen in volledige zinnen in het online logboek. Zijn er nog andere dingen die je wilt onthouden voor de toets? Schrijf deze dan ook op.

  8. Twee personen lopen elkaar tegemoet. Op tijdstip t = 0 zijn ze 60 m van elkaar verwijderd. Persoon A loopt met een snelheid van 2 m/s en persoon B rent met een snelheid van 4,5 m/s. Vind uit op welke plek ze elkaar ontmoeten. Teken hiervoor eerst het bijbehorende (x,t)-diagram.
  9. Een schildpad en een haas proberen elkaar te verslaan in een sprint. Omdat de haas veel vertrouwen heeft in zijn snelheid, geeft hij de schildpad 100 meter voorsprong. De haas heeft een snelheid van 5 m/s. De haas haalt de schildpad in na 25 seconden. Bereken de snelheid van de schildpad. Teken hiervoor eerst het bijbehorende (x,t)-diagram.
  10. Beschrijf hoe je kan bepalen wanneer twee voorwerpen elkaar inhalen of wanneer twee voorwerpen elkaar kruisen. Beschrijf dit in volledige zinnen in het online logboek. Zijn er nog andere dingen die je wilt onthouden voor de toets? Schrijf deze dan ook op.


    11. Bepalen van de snelheid op een tijdstip met een raaklijn.
  11. Klas 4 Bereken de snelheid op tijdstip t = 2s:
  12. Klas 4 Bereken de snelheid op tijdstip t = 5s.
  13. Klas 4 Bereken de beginsnelheid, de eindsnelheid en de snelheid op tijdstip t = 3s.
  14. Klas 4 In het onderstaande diagram wordt de beweging van een bal beschreven die over de grond rolt en tot stilstand komt. Op tijdstip t = 0s werd de bal losgelaten. Wat was de beginsnelheid van de bal?
  15. Klas 4 Bereken de maximale snelheid in het volgende diagram:
  16. Beschrijf hoe je de snelheid kan bepalen op een specifiek moment met behulp van een (x,t)-diagram. Beschrijf dit in volledige zinnen in het online logboek. Zijn er nog andere dingen die je wilt onthouden voor de toets? Schrijf deze dan ook op.